4 3 Greatest Common Divisor and Least Common

4 -3 Greatest Common Divisor and Least Common Multiple Students will be able to understand explain • The greatest common divisor and least common multiple of two or more whole numbers by using a variety of methods. • Applications of GCD and LCM to word problems and their solutions. • The Euclidean algorithm for finding to the greatest common divisor. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 1

Greatest Common Divisor (1 of 3) Two bands are to be combined to march in a parade. A 24 -member band will march behind a 30 -member band. The combined bands must have the same number of columns. Each column must be the same size. What is the greatest number of columns in which they can march? ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 2

Greatest Common Divisor (2 of 3) The bands could each march in 2 columns, and we would have the same number of columns, but this does not satisfy the condition of having the greatest number of columns. The number of columns must divide both 24 and 30. Numbers that divide both 24 and 30 are 1, 2, 3, and 6. The greatest of these numbers is 6. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 3

Greatest Common Divisor (3 of 3) The first band would have 6 columns with 4 members in each column, and the second band would have 6 columns with 5 members in each column. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 4

Definition The greatest common divisor (GCD) or the greatest common factor (GCF) of two whole numbers a and b not both 0 is the greatest whole number that divides both a and b. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 5

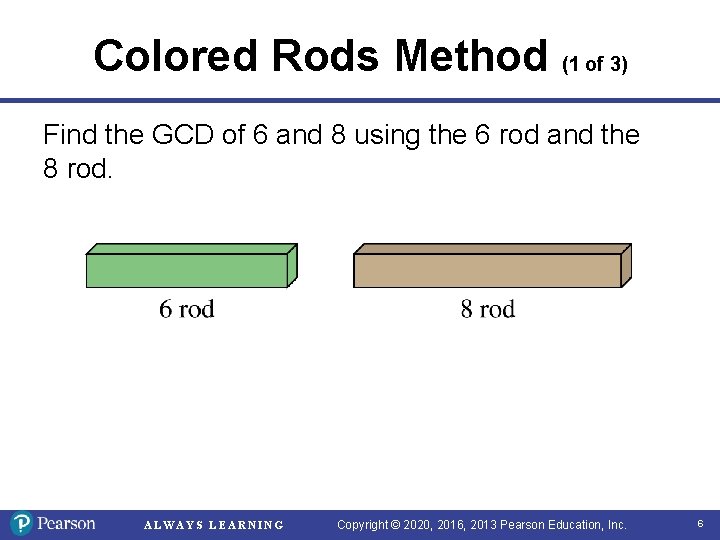
Colored Rods Method (1 of 3) Find the GCD of 6 and 8 using the 6 rod and the 8 rod. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 6

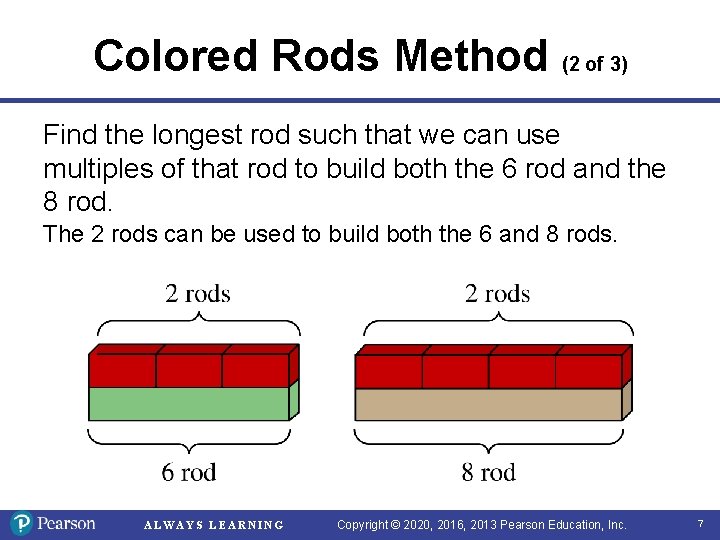
Colored Rods Method (2 of 3) Find the longest rod such that we can use multiples of that rod to build both the 6 rod and the 8 rod. The 2 rods can be used to build both the 6 and 8 rods. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 7

Colored Rods Method (3 of 3) The 3 rods can be used to build the 6 rod but not the 8 rod. The 4 rods can be used to build the 8 rod but not the 6 rod. The 5 rods can be used to build neither. The 6 rods cannot be used to build the 8 rod. Therefore, GCD(6, 8) = 2. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 8

The Intersection-of-Sets Method List all members of the set of whole number divisors of the two numbers, then find the set of all common divisors, and, finally, pick the greatest element in that set. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 9

The Intersection-of-Sets Method To find the GCD of 20 and 32, denote the sets of divisors of 20 and 32 by D 20 and D 32, respectively. D 20 = { 1, 2, 4, 5, 10, 20} D 32 = { 1, 2, 4, 8, 16, 32} Because the greatest number in the set of common positive divisors is 4, GCD(20, 32) = 4. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 10

The Prime Factorization Method To find the GCD of two or more non-zero whole numbers, first find the prime factorizations of the given numbers and then identify each common prime factor of the given numbers. The GCD is the product of the common factors, each raised to the lowest power of that prime that occurs in any of the prime factorizations. Numbers, such as 4 and 9, whose GCD is 1 are relatively prime. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 11

Example 12 Find each of the following: a. GCD(108, 72) b. GCD(0, 13) Because 13 | 0 and 13 | 13, GCD(0, 13) = 13. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 12

Example 12 (continued) c. GCD(x, y) if x = 23 · 72 · 11 · 13 and y = 2 · 73 · 17 GCD(x, y) = 2 · 72 · 13 = 1274 d. GCD(x, y, z) if x = 23 · 72 · 11 · 13, y = 2 · 73 · 17, and z = 22 · 7 GCD(x, y, z) = 2 · 7 = 14 e. GCD(x, y) if x = 54 · 1310 and y = 310 · 1120 Because x and y have no common prime factors, GCD(x, y) = 1. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 13

Calculator Method Calculators with a Simp key can be used to find the GCD of two numbers. Find GCD(120, 180) by pressing the keys: 1 2 0 / 1 8 0 Simp = to obtain the display N/D→n/d 60/90 ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 14

Calculator Method (continued) By pressing the x y key, we see 2 on the display as a common divisor of 120 and 180. By pressing the x Simp = x y y key again and pressing we see 2 again as a factor. Repeat the process to see that 3 and 5 are other common factors. GCD(120, 180) is the product of the common prime factors 2 · 3 · 5, or 60. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 15

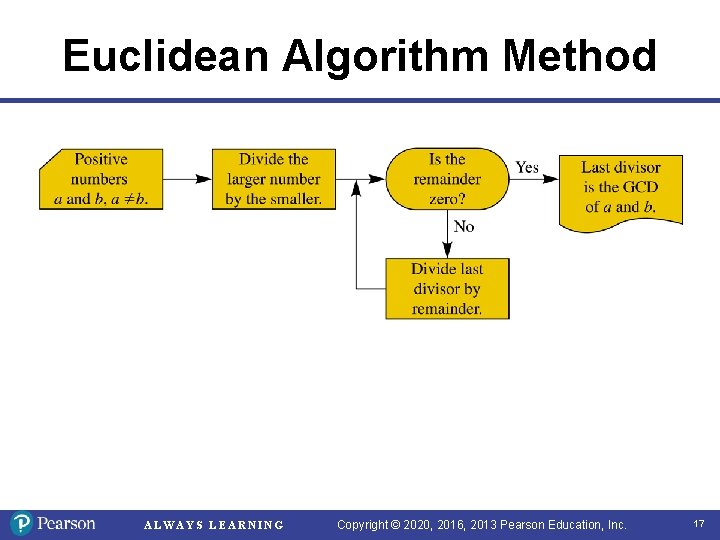
Euclidean Algorithm Method If a and b are any whole numbers with b ≠ 0 and a ≥ b, then GCD(a, b) = GCD(r, b), where r is the remainder when a is divided by b. Finding the GCD of two numbers by repeatedly using theorem above until the remainder is 0 is called the Euclidean algorithm. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 16

Euclidean Algorithm Method ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 17

Example 13 Use the Euclidean algorithm to find GCD(10764, 2300) = GCD(2300, 1564) = GCD(1564, 736) ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 18

Example 13 (continued) GCD(2300, 1564) = GCD(1564, 736) = GCD(736, 92) = GCD(92, 0) = 92 GCD(10764, 2300) = GCD(92, 0) = 92 ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 19

Example 14 a Find GCD(134791, 6341, 6339). Any common divisor of three numbers is also a common divisor of any two of them. The GCD of three numbers cannot be greater than the GCD of any two of the numbers. GCD(6341, 6339) = GCD(6341 − 6339, 6339) = GCD(2, 6339) = 1 GCD(134791, 6341, 6339) cannot be greater than 1, so it must equal 1. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 20

Example 14 b Find the GCD of any two consecutive whole numbers. GCD(n, n + 1) = GCD(n + 1, n) = GCD(n + 1 − n, n) = GCD(1, n) = 1 The GCD of any two consecutive whole numbers is 1. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 21

Least Common Multiple (1 of 2) Hot dogs are usually sold 10 to a package, while hot dog buns are usually sold 8 to a package. What is the least number of packages of each you must buy so that there is an equal number of hot dogs and buns? The number of hot dogs is a multiple of 10, while the number of buns is a multiple of 8. The number of hot dogs matches the number of buns whenever 10 and 8 have multiples in common. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 22

Least Common Multiple (2 of 2) This occurs at 40, 80, 120… The least of these multiples is 40. So we will have the same number of hot dogs and buns by buying 4 packages of hot dogs and 5 packages of buns. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 23

Definition Least Common Multiple (LCM) The least common multiple (LCM) of two nonzero whole numbers a and b is the least non-zero whole number that is simultaneously a multiple of a and a multiple of b. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 24

Number-Line Method Find LCM(3, 4). Beginning at 0, the arrows do not coincide until the point 12 on the number line. Thus, 12 is LCM(3, 4). ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 25

Colored Rods Method (1 of 2) Find LCM(3, 4) using the 3 rod and the 4 rod. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 26

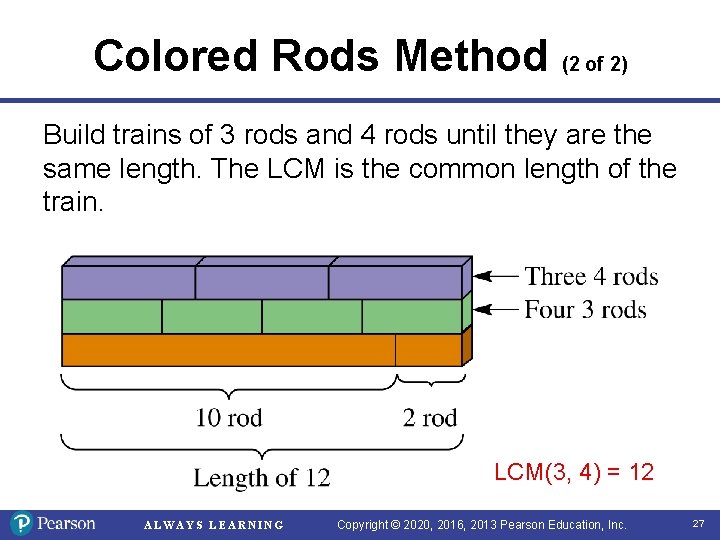
Colored Rods Method (2 of 2) Build trains of 3 rods and 4 rods until they are the same length. The LCM is the common length of the train. LCM(3, 4) = 12 ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 27

The Intersection-of-Sets Method List all members of the set of positive multiples of the two integers, then find the set of all common multiples, and, finally, pick the least element in that set. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 28

The Intersection-of-Sets Method To find the LCM of 8 and 12, denote the sets of positive multiple of 8 and 12 by M 8 and M 12, respectively. Because the least number in the set of common positive multiples is 24, LCM(8, 12) = 24. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 29

The Prime Factorization Method To find the LCM of two non-zero whole numbers, first find the prime factorization of each number. Then take each of the primes that are factors of either of the given numbers. The LCM is the product of these primes, each raised to the greatest power of the prime that occurs in either of the prime factorizations. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 30

Example 15 Find LCM(2520, 10530). ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 31

GCD-LCM Product Method For any two natural numbers a and b, GCD(a, b) · LCM(a, b) = ab. ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 32

Example 16 Find LCM(731, 952). Applying the Euclidean Algorithm, we can determine that GCD(731, 952) = 17. 17 · LCM(731, 952) = 731 · 952 ALWAYS LEARNING Copyright © 2020, 2016, 2013 Pearson Education, Inc. 33