HIGHEST COMMON FACTORH C F AND LOWEST COMMON

HIGHEST COMMON FACTOR(H. C. F. ) AND LOWEST COMMON MULTIPLE(L. C. M. ) Panatda noennil Photakphittayakhom School

Topic 1. Factors 2. Prime Factor 3. Prime Factorization 4. Common Factor 5. Highest Common Factor(H. C. F) 6. Multiples 7. Common Multiple 8. Lowest Common Multiple(L. C. M) 9. Word Problems 2

Learning Objective 1. Recognize prime numbers. 2. Understand the meaning of prime factor and prime factorization. 3. Express the prime factorization of a number in index notation. 4. Find the Highest Common Factor(HCF) and the Lowest Common Multiples(LCM) of two or more numbers 5. Solve word problems. 3

Key words a. Factors ����� b. Prime factor ������� c. Prime Factorization �������� d. Common factors ������� e. Highest Common Factor(H. C. F) ������ (�. �. �( f. Multiples ������ g. Common Multiple ����� h. Lowest Common Multiple(L. C. M) ������� (�. �. �(. 4

Factors What is a factor? When we multiply two or more numbers, we get a product. These numbers are called the FACTORS of the product. Example What is the factor of 15? Multiply 1 ĭ 15 = 15 3 ĭ 5 = 15 From the example above, the number 1, 3, 5 and 15 is a factors of 15 When 15(product) is divided by 1, 3, 5 and 15 (factors), there is not remainder. We can also that 15 is divisible by each of these numbers. 5

Factors Example What is the factors of 32? Solution 1 ĭ 32 = 32 2 ĭ 16 = 32 4 ĭ 8 = 32 The factors of 32 are 1, 2, 4, 8, 16 and 32. Example What is the factors of 48? Solution 1 ĭ 48 = 48 2 ĭ 24 = 48 3 ĭ 16 = 48 4 ĭ 12 = 48 The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48. 6ĭ 8 6

Prime factors What is a Prime numbers? Prime numbers are number which have exactly only two factors, which is 1 and the number itself. The prime numbers within 100 are as follows: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 87 note The digit 1 is not a prime number because it has only one factor, which is 1 by itself. 7

Prime factors A prime factor is a factor of a number that is also a prime number. Example : The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18 and 36. Which numbers are the prime numbers? 2 and 3 are prime numbers. We call 2 and 3 the prime factors of 36. Example What is the factors of 18? 1 ĭ 18 = 18 2 ĭ 9 = 18 3 ĭ 6 = 18 The factors of 18 are 1, 2, 3, 6, 9 and 18. Of these factor 2 and 3 are prime numbers. Therefore 2 and 3 are the prime factors of 18. 8

Prime factors Example What is the factors of 30? 1 ĭ 30 = 30 2 ĭ 15 = 30 3 ĭ 10 = 30 5 ĭ 6 = 30 The factors of 30 are 1, 2, 3, 5, 10, 15 and 30. Of these factor 3 and 5 are prime numbers. Therefore 2, 3 and 5 are the prime factors of 30. Example What is the factors of 35? 1 ĭ 35 = 35 5 ĭ 7 = 35 The factors of 18 are 1, 5, 7 and 35 Of these factor 5 and 7 are prime numbers. Therefore 7 and 5 are the prime factors of 35. 9

Prime Factorization Prime factorization is finding which prime numbers multiply together to make the original number. The number 30, we can express it in terms of prime factors only. 30 = 2 ĭ 3 ĭ 5 Prime factors The above process is known as prime factorization. Example The prime factorization of 28 is what? 28 = 2 ĭ 7 There are two methods to find prime factorization: Factor Tree and Repeated division. 10

Factor Tree Prime factorization of a number can also be obtained by using a factor trees method. Let us express 180 as a product of its prime factors. 180 2 ĭ 9 ĭ 10 2 ĭ 3 ĭ 2 ĭ 5 The prime factorization of 180 = 2 ĭ 3 ĭ 5. 11

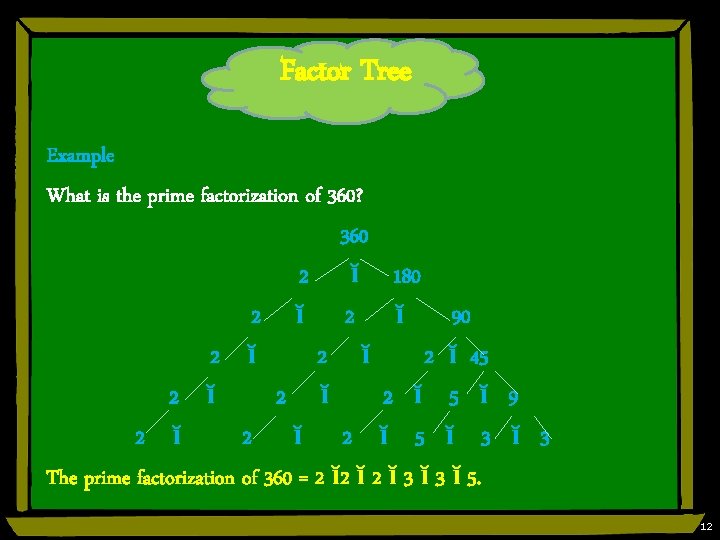
Factor Tree Example What is the prime factorization of 360? 360 2 ĭ 180 2 ĭ 90 2 ĭ 2 ĭ 45 2 ĭ 2 ĭ 5 ĭ 9 2 ĭ 2 ĭ 5 ĭ 3 The prime factorization of 360 = 2 ĭ 2 ĭ 3 ĭ 5. 12

Factor Tree Example What is the prime factorization of 240? 240 2 ĭ 120 2 ĭ 60 2 ĭ 2 ĭ 30 2 ĭ 2 ĭ 15 2 ĭ 2 ĭ 3 ĭ 5 The prime factorization of 240 = 2 ĭ 2 ĭ 3 ĭ 5. 13

Repeated division We can use the repeated division method to find the prime factorization of a number as following: o Divide a number by the smallest prime factor; o Continue dividing by the next prime factor; o Repeat the process until you get 1. 14

Repeated division Example What is the prime factorization of 36? 2 36 2 18 3 9 3 3 1 The prime factorization of 36 = 2 ĭ 3 ĭ 3. 15

Repeated division Example What is the prime factorization of 84? 2 84 2 42 3 21 7 7 1 The prime factorization of 84 = 2 ĭ 3 ĭ 7. 16

Repeated division Example What is the prime factorization of 180? 2 180 2 90 5 45 3 9 3 3 1 The prime factorization of 180 = 2 ĭ 5 ĭ 3. 17

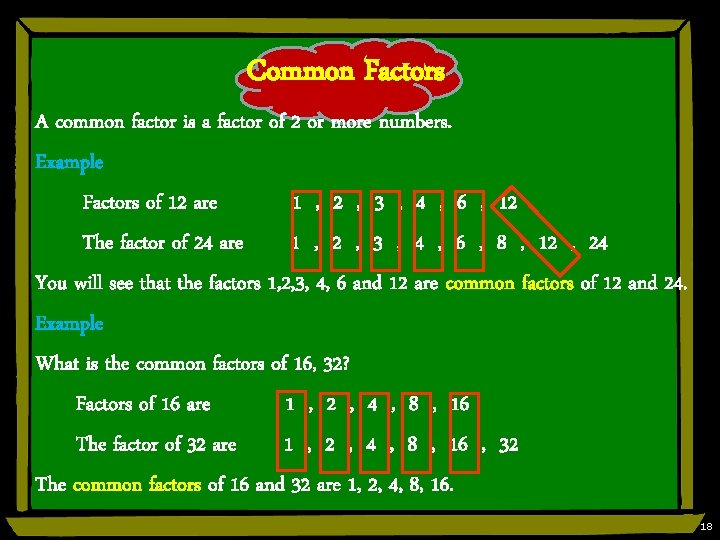
Common Factors A common factor is a factor of 2 or more numbers. Example Factors of 12 are 1 , 2 , 3 , 4 , 6 , 12 The factor of 24 are 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 You will see that the factors 1, 2, 3, 4, 6 and 12 are common factors of 12 and 24. Example What is the common factors of 16, 32? Factors of 16 are 1 , 2 , 4 , 8 , 16 The factor of 32 are 1 , 2 , 4 , 8 , 16 , 32 The common factors of 16 and 32 are 1, 2, 4, 8, 16. 18

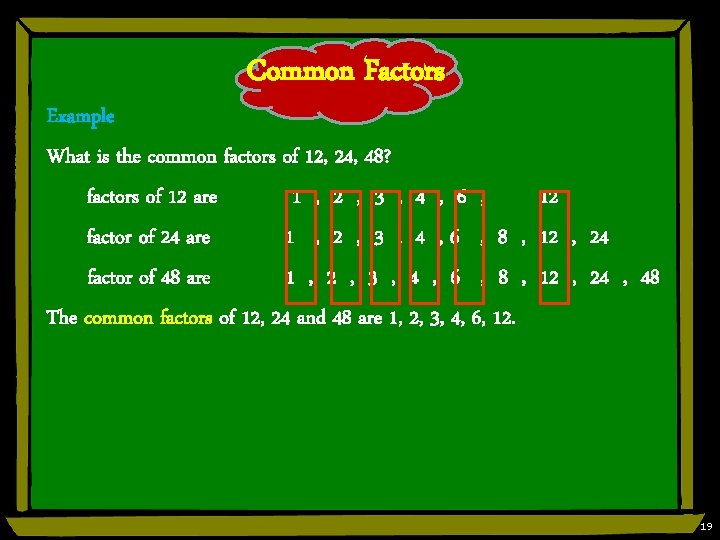
Common Factors Example What is the common factors of 12, 24, 48? factors of 12 are 1 , 2 , 3 , 4 , 6 , 12 factor of 24 are 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 factor of 48 are 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 , 48 The common factors of 12, 24 and 48 are 1, 2, 3, 4, 6, 12. 19

Highest Common Factors The largest common factor of two or more numbers is called the highest common factor (HCF). Example Factors of 12 are 1 , 2 , 3 , 4 , 6 , 12 The factor of 24 are 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 You will see that the factors 1, 2, 3, 4, 6 and 12 are common factors of 12 and 24. And from the common factors you will see that the HIGHEST COMMON FACTORS (H. C. F. ) of 12 and 24 is 12. ANOTHER METHOD We can also find the HCF by using Prime Factorization method and Repeated Division method. 20

Highest Common Factors Method 1 : Using Prime Factorization. Example Find the highest common factor of 15 and 30. 15 = 3 ĭ 5 30 = 3 ĭ 5 ĭ 2 3 ĭ 5 = 15 Therefore, the highest common factors of 15 and 30 is 15. 21

Highest Common Factors Method 1 : Using Prime Factorization. Example Find the highest common factor of 12, 24 and 36. 12 = 2 ĭ 3 24 = 2 ĭ 3 ĭ 2 36 = 2 ĭ 3 ĭ 3 Therefore, the highest common factors of 12, 24 and 36 is 2 ĭ 3 = 12. 22

Highest Common Factors Method 1 : Using Prime Factorization. Example Find the highest common factor of 9 , 18 , 27 and 36. 9 = 3 ĭ 3 18 = 3 ĭ 2 27 = 3 ĭ 3 36 = 3 ĭ 2 ĭ 2 Therefore, the highest common factors of 9, 18, 27 and 36 is 3 ĭ 3 = 9. 23

Highest Common Factors Method 2 : Using Repeated Division. Example Find the highest common factor of 10 and 30. 2 10, 30 Divide by the smallest common prime factor 2 5 5, 15 Divide by common prime factor 5 1, 3 Stop here as 1 is the only common factor. H. C. F. is 2 ĭ 5 = 10 Therefore, the highest common factors of 10 and 30 is 10. 24

Highest Common Factors Method 2 : Using Repeated Division. Example Find the highest common factor of 16, 32 and 48. 2 16, 32, 48 Divide by the smallest common prime factor 2 2 8, 16, 24 Divide by common prime factor 2 2 4, 8, 12 Divide by common prime factor 2 2 2, 4, 6 Divide by common prime factor 2 1, 2, 3 Stop here as 1 is the only common factor Therefore, the highest common factors of 16, 32 and 48 is 2 ĭ 2 ĭ 2 = 16. 25

Highest Common Factors Method 2 : Using Repeated Division. Example Find the highest common factor of 9, 18, 27 and 36. 3 9, 18, 27, 36 Divide by the smallest common prime factor 3 3 3, 6, 9, 12 Divide by common prime factor 3 1, 2, 3, 4 Stop here as 1 is the only common factor. Therefore, the highest common factors of 9, 18, 27 and 36 is 3 ĭ 3 = 9. 26

Multiples The products of a number with the natural numbers 1, 2, 3, 4, 5, . . . are called the multiples of the number. A multiple of a number, say 2 is a number that can be divided exactly by 2. 2, 4, 6, 8, 10. . . . are multiples of 2. 1ĭ 5=5 2 ĭ 5 = 10 3 ĭ 5 = 15 The first five multiples of 5 are 5, 10, 15, 20 and 25. 4 ĭ 5 = 20 5 ĭ 5 = 25 The numbers 5, 10, 15, 20, . . . are called the multiples of 5. 27

Multiples Example What is the multiple of 3? 1ĭ 3=3 2ĭ 3=6 3ĭ 3=9 4 ĭ 3 = 12 The multiple of 3 is 3, 6, 9, 12, . . . Example List the first five numbers of 8. Answer : The first five numbers of 8 are 8, 16, 24, 32 and 40. 28

Multiples Example Is 30 a number of each of the following numbers. a) 7 b) 15 Solution a) 30 7 = 4 remainder 2 cannot be divided equally Therefore, 30 is not a multiple of 7. b) 30 15 = 2 An exact division with no remainder Therefore, 30 is a multiple of 15. 29

Common Multiples that are common to two or more numbers are said to be common multiples. Example The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, . . . . The multiples of 3 are 3, 6, 9, 12, 15, 18, . . . . The common multiples of 2 and 3 are 6, 12, 18, . . . Example The multiples of 10 are 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, . . The multiples of 20 are 20, 40, 60, 80, 100, 120, . . . . The multiples of 30 are 30, 60, 90, 120, 150, 180, . . . . The common multiples of 10, 20 and 30 are 60, 120, . . . 30

Lowest Common Multiples The smallest common multiple of two or more numbers is called the lowest common multiple (LCM). Example The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, . . . . The multiples of 3 are 3, 6, 9, 12, 15, 18, . . . . The common multiples of 2 and 3 are 6, 12, 18, . . . The lowest common multiples of 2 and 3 is 6. ANOTHER METHOD We can also find the L. C. M. by using Prime Factorization method and Repeated Division method. 31

Lowest Common Multiples Method 1 : Using Prime Factorization. Example Find the lowest common multiples of 15 and 30. 15 = 3 ĭ 5 30 = 3 ĭ 5 ĭ 2 = 30 Therefore, the lowest common multiples of 15 and 30 is 30. 32

Lowest Common Multiples Method 1 : Using Prime Factorization. Example Find the lowest common multiples of 12 , 24 and 36. 12 = 2 ĭ 3 24 = 2 ĭ 3 ĭ 2 36 = 2 ĭ 3 ĭ 3 2 ĭ 3 ĭ 2 ĭ 3 = 72 Therefore, the lowest common multiples of 12, 24 and 36 is 72. 33

Lowest Common Multiples Method 1 : Using Prime Factorization. Example Find the highest common factor of 9 , 18 , 27 and 36. 9 = 3 ĭ 3 18 = 3 ĭ 2 27 = 3 ĭ 3 36 = 3 ĭ 2 ĭ 2 Therefore, the lowest common multiples of 9 , 18 , 27 and 36 is 3 ĭ 3 ĭ 2 = 108. 34

Lowest Common Multiples Method 2 : Using Repeated Division. Example Find the lowest common multiples of 10 and 30. 2 10, 30 5 5, 15 3 1, 1 L. C. M. is 2 ĭ 3 ĭ 5 = 30 Therefore, the lowest common multiples of 10 and 30 is 30. 35

Lowest Common Multiples Method 2 : Using Repeated Division Example Find the lowest common multiples of 16, 32 and 48. 2 16, 32, 48 - Divide the numbers by the smallest divisible 2 8, 16, 24 prime number first. 2 4, 8, 12 - Continue dividing until all the numbers are 2 2, 4, 6 reduced to one. 2 1, 2, 3 2 1, 1, 3 Therefore, the lowest common multiples of 16, 32 and 48 is 2 ĭ 2 ĭ 2 ĭ 3 = 192. 36

Lowest Common Multiples Method 2 : Using Repeated Division Example Find the lowest common multiples of 9, 18, 27 and 36. 3 9, 18, 27, 36 - Divide the numbers by the smallest divisible 3 3, 6, 9, 12 prime number first. 2 1, 2, 3, 4 - Continue dividing until all the numbers are 3 1, 1, 3, 2 reduced to one. 1, 1, 1, 2 Therefore, the lowest common multiples of 9, 18, 27 and 36 is 3 ĭ 3 ĭ 2 = 108 37

Word Problems Example What is the lest number, which when divided by 12, 15, 20 and 54 leaves in each case a remainder of 8? Solution 1. Find L. C. M. of numbers 12, 15, 20 and 54 using short division as follows. 2 12, 15, 20, 54 2 6, 15, 10, 27 3 3, 15, 5, 27 5 1, 5, 5, 9 1, 1, 1, 9 Therefore, L. C. M. of 12, 15, 20 and 54 = 2 ĭ 3 ĭ 5 ĭ 9 = 540 38

Word Problems 2. Find the least number, which when divided by 12, 15, 20 and 54 leave in each case a remainder of 8. The require number = (L. C. M. of numbers 12, 15, 20 and 54) +8 = 540 + 8 = 548 39

Word Problems Example A flash bulb on a Christmas tree flashes once every 12 seconds, and the other bulb flashes once every 15 seconds. If they are flashing together now, how long will it take for the two bulbs to flash together again? Solution We shall find the lowest common multiple of 12 and 15. Multiples of 12 : 12, 24, 36, 48, 60, . . . . Multiples of 15 : 15, 30, 45, 60, . . . . L. C. M. of 12 and 15 is 60. Therefore, If the two bulbs are flashing together now, after 60 seconds the two bulbs will flash together again. 40

Word Problems Example There are 126 pieces of cupcakes and 84 pieces of cookies. The cupcakes and cookies are divided into packs with equal number of pieces of cupcakes and cookies. What is the greatest possible number of packs needed? Solution We shall find the highest common factors of 84 and 126. 84 = 2 ĭ 3 ĭ 7 126 = 2 ĭ 3 ĭ 7 The highest common factors of 84 and 126 is 42. Therefore, the greatest possible number of packs is 2. 41

Word Problems Example A rectangle piece of card board measuring 360 cm by 280 cm is cut into small identical squares of the largest possible length. Find a) The length of a side of each square, b) The number of square card formed. Solution We shall find the highest common factors of 280 and 360. 280 = 2 ĭ 2 ĭ 5 ĭ 7 360 = 2 ĭ 2 ĭ 5 ĭ 9 The highest common factors of 280 and 360 is 40. Therefore, The length of a side of each square is 9 cm and 7 cm and the number of square card formed is 40. 42

Summary 1. The factors of a number divide the number exactly. 2. Prime numbers are numbers which have exactly two factors, namely 1 and the number itself. 1 is not a prime number. 3. Prime factorization is the method of expressing a number as a product of its prime factors. 4. The H. C. F. is the largest common factor among all of the common factors of two or more numbers. 5. Multiples of a number are obtained by multiplying the number by whole numbers. 6. The L. C. M. is the smallest common multiple among all the common multiples of two or more numbers. 43