Greatest Common Factor and Least Common Multiples GCF

Greatest Common Factor and Least Common Multiples GCF and LCM

What is the difference between a factor and a multiple?

Give me an example of a factor of 15

Give me an example of a multiple of 15

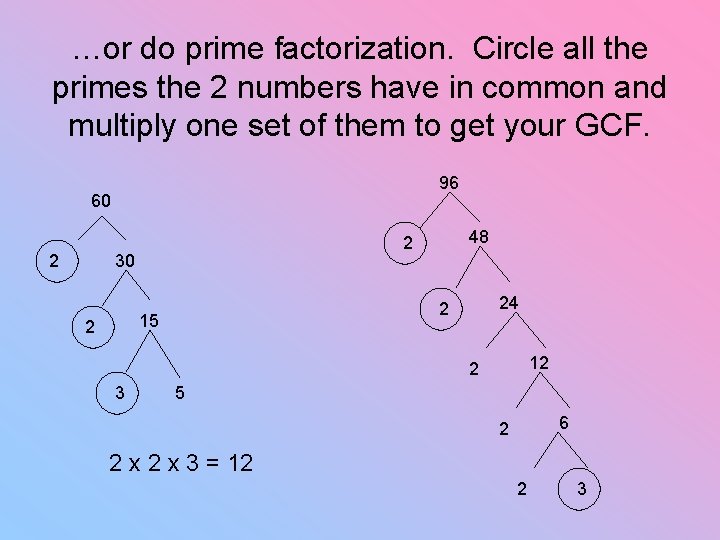
How would you find the GCF of 60 and 96?

There actually 2 ways. You can use prime factorization, or write out all the prime factors for each number.

List the factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 List the factors of 96 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 find the largest factor - 12

…or do prime factorization. Circle all the primes the 2 numbers have in common and multiply one set of them to get your GCF. 96 60 2 30 24 2 15 2 48 2 12 2 3 5 6 2 2 x 3 = 12 2 3

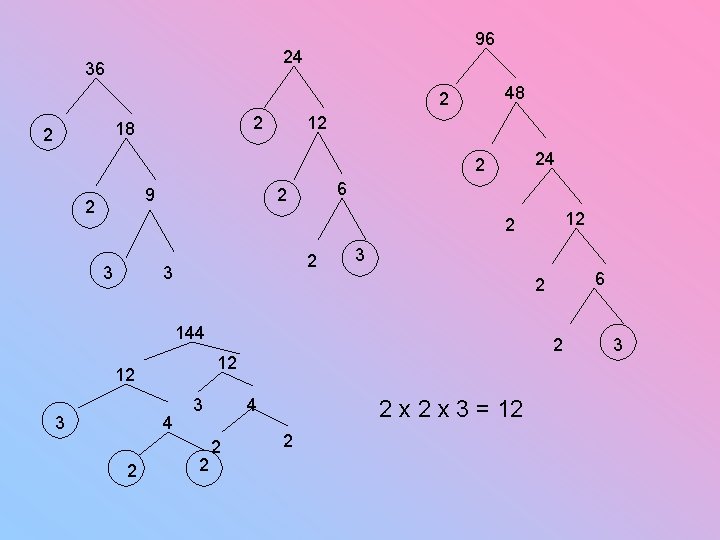
Find the GCF (HCF) of 36, 24, 144 and 96

96 24 36 48 2 2 18 2 12 24 2 9 2 6 2 12 2 3 3 144 4 2 2 12 12 3 6 2 3 2 4 2 2 x 3 = 12 2 3

There are 2 ways to find the LCM as well. You can list the multiples of the numbers or do prime factorization. Find the LCM of 12 and 18

Multiples of 12 are… 12, 24, 36, 48, 60, 72, …. Multiples of 18 are… 18, 36, 54, 72, 90, 108, … The smallest multiple the 2 numbers have in common is the least common multiple.

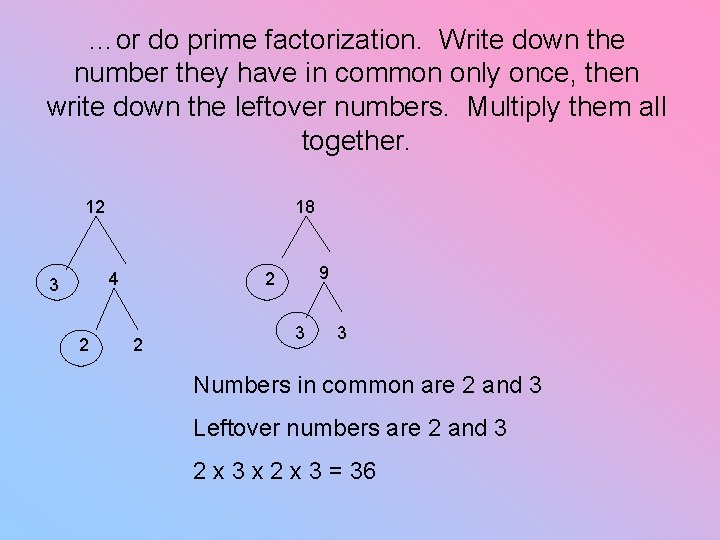
…or do prime factorization. Write down the number they have in common only once, then write down the leftover numbers. Multiply them all together. 12 18 4 3 2 9 2 2 3 3 Numbers in common are 2 and 3 Leftover numbers are 2 and 3 2 x 3 x 2 x 3 = 36

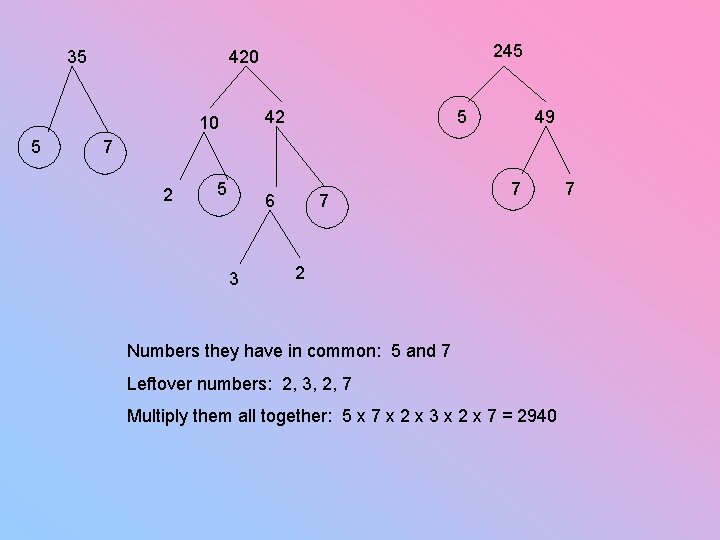
Find the LCM of 35, 420 and 245

35 42 10 5 245 420 5 49 7 2 5 6 3 7 7 2 Numbers they have in common: 5 and 7 Leftover numbers: 2, 3, 2, 7 Multiply them all together: 5 x 7 x 2 x 3 x 2 x 7 = 2940 7