Least Common Multiples And Greatest Common Factor 1

Least Common Multiples And Greatest Common Factor 1

Lesson 3. 4. 5 Least Common Multiples California Standards: What it means for you: Number Sense 2. 1 Solve problems involving addition, subtraction, multiplication, and division of positive fractions and explain why a particular operation was used for a given situation. Number Sense 2. 4 Determine the least common multiple and the greatest common divisor of whole numbers; use them to solve problems with fractions (e. g. , to find a common denominator to add two fractions or to find the reduced form for a fraction). You’ll learn how to find the lowest number that two numbers both divide into exactly. You’ll also see how this can help you with adding and subtracting fractions. Key words: • least common multiple • greatest common factor 2

Lesson 3. 4. 5 Least Common Multiples Today we are going to learn about Lowest The Least Common ulte Is Less Than the Others Common Multiples and Greatest Common Factor. First let’s examine the parts of a multiplication equation. MULTIPLE 3

Lesson 3. 4. 5 Least Common Multiples Definition Least Common Multiple (LCM): The lowest multiple of two or more numbers. Example: What is the LCM of 10 and 30? 10 x 1 = 10 10 x 2 = 20 10 x 3 = 30 10 x 4 = 40 10 x 5 = 50 10 x 6 = 60 30 x 1 = 30 30 x 2 = 60 30 x 3 = 90 So the least common multiple of 10 and 30 is 30. 4

Lesson 3. 4. 5 Least Common Multiples When do you use LCM? The Least Common ulte Is Less Than the Others 2 + 1 10 30 When you need to add fractions with different denominators! 5

Lesson 3. 4. 5 Least Common Multiples Definition Greatest Common Factor (GCF): The largest factor shared by two or more numbers. Example: What is the GCF of 20 and 30? 1 x 20 2 x 10 4 x 5 1 x 30 2 x 15 3 x 10 5 x 6 The factors of 20 are 1, 2, 4, 5, 10, and 20 The factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30 6

Lesson Least Common Multiples 3. 4. 5 When do you use GCF? The Least Common ulte Is Less Than the Others 20 30 When you need to SIMPLIFY fractions! 7

Lesson 3. 4. 5 Least Common Multiples You can find the Lowest Common Multiple The Least. Than the Others (LCM) and the Greatest Common Factor (GCF) with a factor tree. Let’s try some! 8

Lesson 3. 4. 5 Example Least Common Multiples 1 Find the LCM and GCF of 20 and 12. Solution So the least common multiple of 20 and 12 is 60. 9 Solution follows…

Lesson 3. 4. 5 Example Least Common Multiples 2 Find the LCM and GCF of 16 and 28. Solution So the least common multiple of 16 and 28 is 112. 10 Solution follows…

Lesson Least Common Multiples 3. 4. 5 Example 3 Find the LCM and GCF of 12 and 44. . Solution So the least common multiple of 12 and 44 is: 12 × 44 ÷ 4 = 132 11 Solution follows…

Lesson 3. 4. 5 Least Common Multiples Guided Practice Find the least common multiple and greatest common factor. 1. 4, 40 2. 15, 50 3. 12, 9 4. 10, 25 12 Solution follows…

Lesson 3. 4. 5 Least Common Multiples Independent Practice Find the LCM and GCF. 7. 30, 45 8. 4, 12 9. 14, 21 10. 28, 30 13 Solution follows…

LCM and GCF: Fractions with Different Denominators 14

Lesson LCM and GCF 3. 4. 5 Example 1 1 1 What is + ? 3 5 Solution: 1 1 5 3 5 + 3 8 + = = = + 3 5 15 15 15

Lesson LCM and GCF 3. 4. 5 Example 2 3 5 What is - ? 40 16 16

Lesson 3. 4. 5 Example LCM and GCF 3 What is 2 ½ + 3 ¼ = 17

Lesson 3. 4. 5 Least Common Multiples Guided Practice Use factor trees to find the GCF and LCM. Solve the equations once they have the same denominator. 1. 13 9 = + 10 15 3. 1 5 = + 6 10 39 18 57 19 + = = 30 30 30 10 5 15 20 2 + = = 30 30 30 3 2. 4 5= 8 + + 9 6 18 4. 5 1 = 20 – 3 = 17 – 6 8 24 24 24 15 23 = 18 18 18 Solution follows…

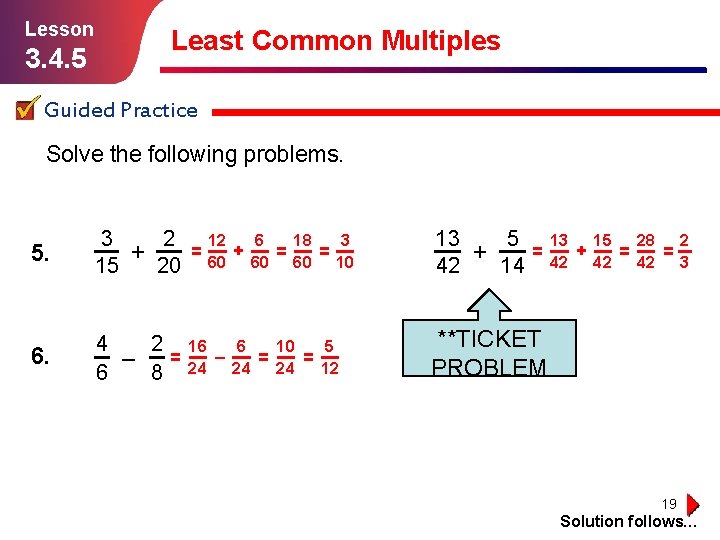
Lesson 3. 4. 5 Least Common Multiples Guided Practice Solve the following problems. 5. 3 2 = + 15 20 6. 4 2 = – 6 8 12 6 18 3 + = = 60 60 60 10 16 6 10 5 – = = 24 24 24 12 13 5 = + 42 14 13 15 28 2 + = = 42 42 42 3 **TICKET PROBLEM 19 Solution follows…

Lesson 3. 4. 5 Least Common Multiples Independent Practice Find the LCM and GCF for problems 7 -15 by making factor trees. Then add or subtract the fractions. 2 1 – 3 4 3 1 – 4 2 5 12 8. 10. 2 + 15 10 25 4 5 11. 8 – 5 9 6 8 18 + 11 44 25 22 14. 7. 13 12 + 15 18 1 2 + 9 7 1 4 9. 1 18 12. 13 – 3 12 4 23 15 15. 9 9 – 10 14 25 63 1 3 9 35 20 Solution follows…

Lesson 3. 4. 5 Least Common Multiples Independent Practice Work out the sums and differences in Exercises 26– 31. Give your answers in their simplest form. 26. 7 15 + 75 35 29. 10 + 6 49 21 274 525 27. 4 – 1 27 45 24 49 30. 7 1 + 9 30 17 135 28. 1 + 15 24 56 13 42 73 90 31. 31 – 10 42 56 47 84 21 Solution follows…

Lesson 3. 4. 5 Least Common Multiples Round Up Pausing for a second to find the least common multiple before trying to add or subtract two fractions with different denominators is a good way to avoid having to deal with really big numbers. Smaller numbers also make simplifying at the end easier. 22