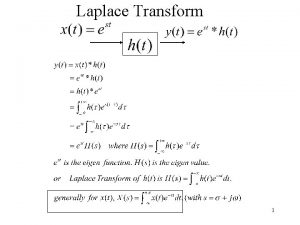Unit 2 Relations and Functions Introduction to Relation















































































![i) gof solution: gof(x)=g[f(x)] =g[x+2] =x+2 -2 =x ii) fog solution: f[g(x)] =f[x-2] = i) gof solution: gof(x)=g[f(x)] =g[x+2] =x+2 -2 =x ii) fog solution: f[g(x)] =f[x-2] =](https://slidetodoc.com/presentation_image_h/8a66645ac8ba0c1a1af07d91bf3a5844/image-100.jpg)
![iii) gog solution: gog(x) =g[x-2] =x-2 -2 =x-4 iv) fof solution: fof(x) = f[x+2] iii) gog solution: gog(x) =g[x-2] =x-2 -2 =x-4 iv) fof solution: fof(x) = f[x+2]](https://slidetodoc.com/presentation_image_h/8a66645ac8ba0c1a1af07d91bf3a5844/image-101.jpg)
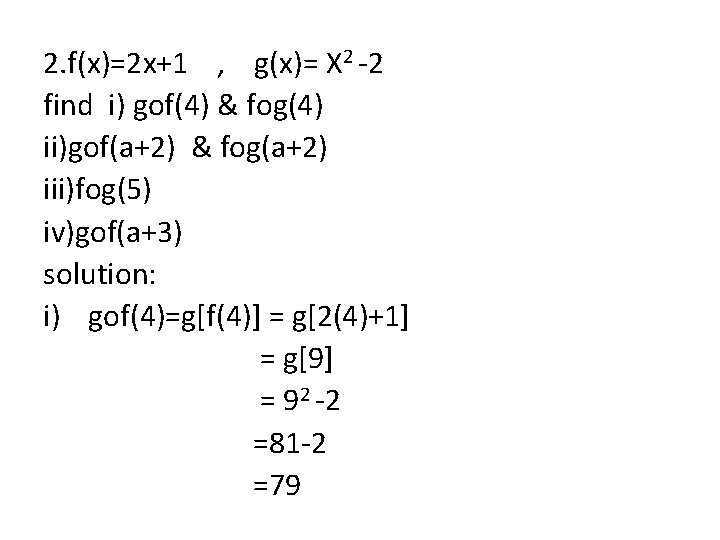




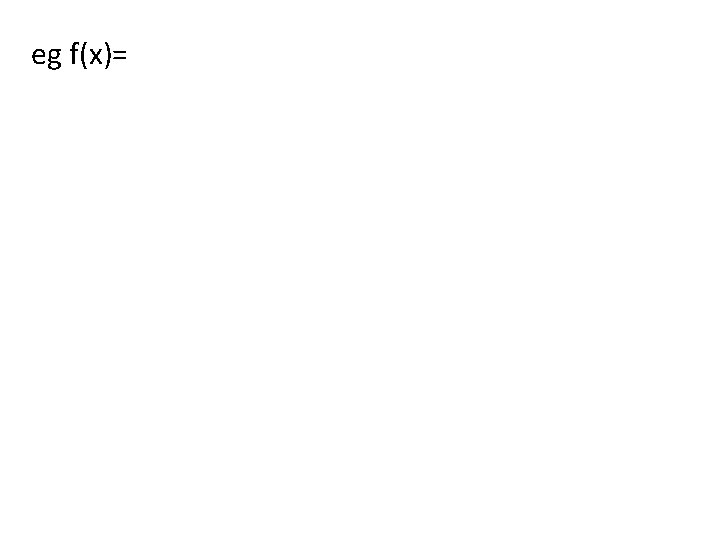


- Slides: 109

Unit 2 Relations and Functions

Introduction to Relation • A relation is a type of association that exists between two or more elements. • Consider the eg. 1. x is father of y. 2. x was born in the city y in the year z. 3. The number x is greater than number y. • In general one can have relation with ‘n’ objects. (where n is positive integer) • In describing the relation, it is necessary not only to specify the objects but also the order in which they appear.

Necessary ordering of objects • An ordered n- tuple, for n>0, is a sequence of objects , denoted by (a 1 , a 2, -----an). • If n=2, the ordered n-tuple is called an ordered pair. • If n=3, the ordered n-tuple is called an ordered triple and so on.

Application of relation • We can describe languages (e. g. , compiler grammar, a universal Turing machine) using sets and set relations. • Graph traversal requires sets to track node visits. • Data structures are inherently set-based. • Relational databases are entirely premised on set theory insofar as table operations are concerned.

Product set (cartesian product) • Let A & B be non empty sets. we define the product set (AXB)as. AXB = {(a, b)| a ε A and b ε B} If A= Ø or B= Ø, then AXB= Ø Eg. Let A={a, b, c}, B={1, 2} then AXB=? Solution: AXB: {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)} • The product set is not commutative i. e. AXB ≠ BXA

• following theorem establishes certain important properties of the product operation Theorem: If A, B, C are sets then 1. Ax(B U C)= (AXB) U (AXC) 2. AX(B ᴒ C) = (AXB) ᴒ (AXC) 3. (A U B)XC=(AXC) U (BXC) 4. (A ᴒ B)XC = (AXC) ᴒ (BXC)

• Theorem: If A and B are finite sets with cardinalities m, n resp. then |Ax. B|=m. n Proof: since |A|=m Let A={a 1 , a 2, -----am}, Similarly , |B|=n Let B={b 1 , b 2, -----bn} Now AXB={(ai, bj)|1<=i<=m, 1<=j<=n} Since for each element ai in A there exist a corresponding element bj in B in ordered pair (ai , bj), the set AXB consists of exactly m. n elements hence |AXB|=m. n Is proved Eg. If A={n ∈ N|1<=n<=100} , B={n ∈N|1<=n<=50} Then AXB = 100 X 50= 5000


• Empty relation: if R= Ø, then that relation is called empty or void relation. • If R=A 1 XA 2 XA 3 X-----An, then R is called the universal relation. • If R=1, 2 or 3 then R is called unary, binary or ternary relation. • Eg. 1 Let A={1, 2, 5, 6} and let R be relation characterized by the property “x is less than y” then R={(1, 2), (1, 5), (1, 6), (2, 5), (2, 6), (5, 6)} where R is binary. Eg 2. Let A={1, 2, 3} and R be the relation characterized by the property “x+y is less than equal to z” then R is{(1, 2, 3)} is ternary.

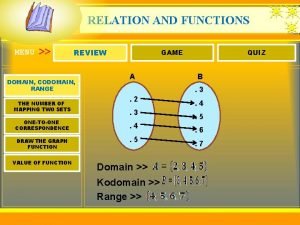
Binary Relation • Let A and B are non empty sets. Then binary relation R from A to B is subset of AXB, i. e. R c AXB. • The Domain of R is denoted by D(R), is the set of elements in A that are related to some elements in B i. e. D(R)= {a ε A|for some b ε B, (a, b) ε R} • The range of R denoted by Rn (R) is the set of elements in B that are related to some element in A i. e. Rn (R)={b ε B|for some a ε A, (a, b) ε R} Clearly we can say D(R) c A and Rn (R) c B

Eg. Let A={2, 3, 4, 5} and let R be the relation on A defined as a. Rb iff a<b find D(R) & Rn (R) Solution: R={(2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)} Then D(R)={2, 3, 4} , Rn (R) ={3, 4, 5}

Complement of relation (R ) • A relation as a set has its complement, which is defined below • The complement of relation R, denoted by R , is defined as. R ={(a, b)|(a, b) ∉ R} i. e. a. Rb iff a. Rb Eg. Let A ={1, 2, 3, 4} and B={a, b, c} Let R ={(1, a)(1, b), (2, c), (3, a), (4, b)} & S={(1, b), (1, c), (2, a), (3, b), (4, b)} Find 1. R and S 2. verify Demorgan’s law for R and S

1. R and S =? Solution: AXB={(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c), (4, a), (4, b), (4, c)} R = {(1, c), (2, a), (2, b), (3, c), (4, a), (4, c)} S = {(1, a), (2, b), (2, c), (3, a), (3, c), (4, a), (4, c)} 2. Demorgan’s law states that – RUS =RᴒS R U S ={(1, a), (1, b), (1, c), (2, a), (2, c), (3, a), (3, b), (4, b)} R U S ={(2, b), (3, c), (4, a), (4, c)} R ᴒ S ={(2, b), (3, c), (4, a), (4, c)} Therefore R U S = R ᴒ S

Eg. R ᴒ S = R U S

Converse of Relation (Rc) • Given a relation from A to B one may define a relation from B to A as follows. Let R be a relation from A to B then the converse of R, denoted by Rc is the relation form B to A defined as. Rc = {(b, a)|(a, b) ∈ R} Clearly we can say Rc c BXA. If A=N the set of natural number and R is the relation <, then Rc is the relation >. The converse relation is also called as the inverse relation and is denoted by R-1.

• Following theorem gives important properties of the converse relation • Let R , S be the relations from A to B then – i) (Rc )c =R ii) (RUS) c = R c U S c iii) (R ᴒ S) c = R c ᴒ S c Eg. Let A ={1, 2, 3, 4} and B={a, b, c} Let R={(1, a), (3, c)} Find i) R c ii) D(R c ) iii) Rn (R c)

i) R c ={(a, 1), (a, 3), (c, 3)} ii) D(R c )= {(a, c)} = Rn (R) iii) Rn (R c)={(1, 3)} = D(R)

Composition of binary relation (R 1. R 2) • Relations that are formed from an existing sequence of relation. They are called as composite relation. • The concept of composite relation plays an important role in the execution of program where a sequence of data conversion takes place from decimal to binary and from binary to floating point. • Definition- Let R 1 is a relation from A to B and R 2 be the relation from B to C. The composite relation from A to C denoted by R 1. R 2 or (R 1 R 2) is defined as-

R 1. R 2= {(a, c)|a ε A ᴒ c ε C ᴒ ⱻ b[b ε B ᴒ (a, b) ε R 1 ᴒ (b, c) ε R 2]} • If R 1 is a relation from A to B and R 2 is the relation from C to D, R 1. R 2 is not defined unless B=C. • The operation of composite relation is not commutative. i. e. R 1. R 2 ≠ R 2. R 1 Eg. Let A={a, b, c, d} where R 1={(a, a), (a, b), (b, d)} and R 2={(a, d), (b, c), (b, d), (c, b)} Find R 1. R 2=? , R 2. R 1=? , R 2 2 =?

1. R 2 = {(a, d), (a, c)} 2. R 1 = {(c, d)} 3. R 2 2 = {(b, b), (c, c), (c, d)} Eg 2. Let A={2, 3, 4, 5, 6} and let R 1. R 2 be the relations on A such that. R 1={(a, b)|a-b=2} and R 2={(a, b)|a+1=b or a=2 b} find composite relation i)R 1. R 2 ii)R 2. R 1 iii) R 1 2

Solution: R 1={(4, 2), (5, 3), (6, 4)} R 2={(2, 3), (3, 4), (4, 5), (5, 6), (4, 2), (6, 3)} i)R 1. R 2 ={(4, 3), (5, 4), (6, 5), (6, 2)} ii)R 2. R 1={(3, 2), (5, 4), (4, 3)} iii) 2 =? R 1

Matrix representation of a relation(MR ) • Let A={a 1, a 2, ----am } and B={b 1, b 2, ----- bn} be finite sets containing resp. m & n elements. • Let R be the relation from A to B by definition R c AXB , hence we can represent R by a m. Xn matrix MR=[mij], which is defined as follows mij = 1 if (ai, bj)ε R =0 if (ai, bj) ∉ R

eg. 1 Let A={a, b, c, d} and B={1, 2, 3} Let R={(a, 1), (a, 2), (b, 1), (c, 2), (d, 1)} find the relation matrix Solution: MR will have 4 rows and 3 column MR = 1 1 0 1 0 0 0 0 Eg. 2 Let A={1, 2, 3, 4, 8} , B={1, 4, 6, 9} let a. Rb iff b/a find the relation matrix

Solution: R={(1, 1), (1, 4), (1, 6), (1, 9), (2, 4), (2, 6), (3, 9), (4, 4)} MR = 1 0 0 1 1 1 0 0 Eg. Let A = {a, b, c, d} and let MR = Find R 1 0 0 1 1 1 0

Relation Matrix operation • A relation matrix has entries which are either one or zero, such a matrix is called Boolean matrix. • Let A= [aij] and B= [bij] be mxn Boolean matrix we define. A+B =[ cij] where cij = 1 if aij = 1 or bij = 1 = 0 if aij & bij are both zero similarly if A= [aij] is an mxn boolean matrix and B= [bij] is an nxr matrix then A. B = [dij] an mxr matrix. where dij = 1 if aij = bij =1 = 0 if aij = 0 or bij =0

eg A= 1 0 1 1 0 then A+ B= 1 1 1 0 and B= 1 0 0 1 A. B = 1 1 0 1 1 • Properties of Relation matrix: Let R 1 be a relation from A to B, R 2 from B to C. Then the relation metrices satisfy the following properties. 1. MR 1. R 2 = MR 1 x MR 2 2. MRc = transpose of MR

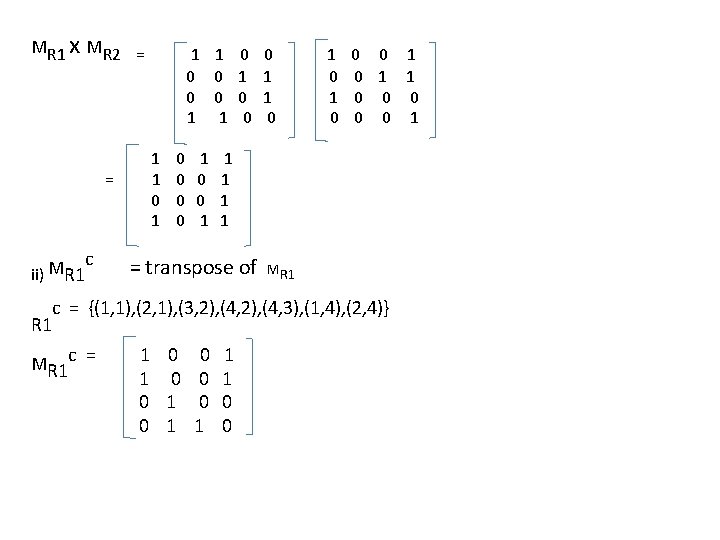
eg. 1 Let A= {1, 2, 3, 4} and let R 1={(1, 1), (1, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 2)} R 2={(3, 1), (4, 4), (2, 3), (2, 4), (1, 1), (1, 4)} verify i) MR 1. R 2 = MR 1 x MR 2 solution: MR 1 = 1 1 0 0 0 1 1 0 MR 2 = 1 0 0 0 0 1 1 0 1 R 1. R 2 = {(1, 1), (1, 4), (1, 3), (2, 1), (2, 4), (3, 4), (4, 1), (4, 3)} MR 1. R 2 = 1 0 1 1 1 0 0 0 1 1

MR 1 x MR 2 = = c M ii) R 1 1 1 0 0 1 1 0 0 0 0 1 1 0 0 0 1 1 1 = transpose of MR 1 c = {(1, 1), (2, 1), (3, 2), (4, 3), (1, 4), (2, 4)} MR 1 c = 1 0 0 0 1 1 0 0

Graphical representation of a relation • If A is a finite set and R is a relation on A, it is possible to represent R pictorically by means of a graph • The element of A are represented by points or circles called as nodes or vertices. • if a. Rb , this is indicated by drawing an arc from a to b with an arrow head pointing in the direction a b • If a. Ra , this is shown by drawing a loop around a. • These arcs or loop are called as edges of the graph. • The resulting graph is called a directed graph of diagraph of R.

eg. Let A={2, 3, 4, 5} and let R={(2, 3), (3, 2), (3, 4), (3, 5), (4, 3), (4, 4), (4, 5)} draw its diagraph Solution:

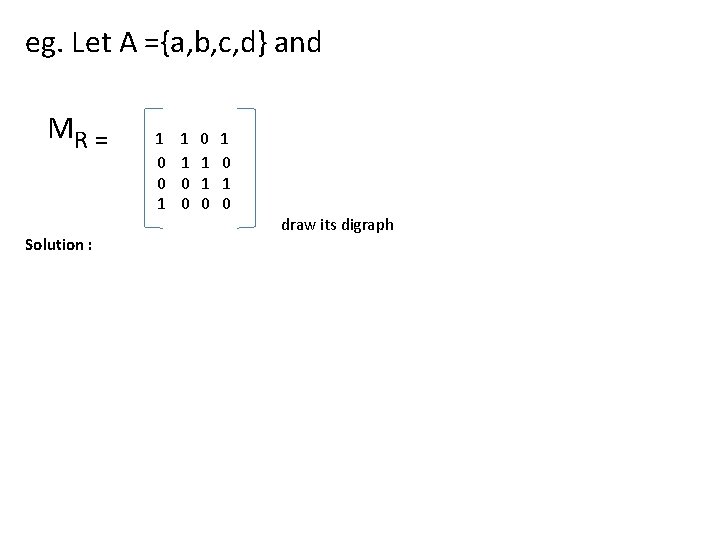
eg. Let A ={a, b, c, d} and MR = Solution : 1 0 0 1 1 1 0 0 0 1 1 0 1 0 draw its digraph

Special properties of binary relation • Let R be a relation on a set A 1. Reflexive relation(a. Ra) R is reflexive if for every element a ∈ A, a. Ra i. e. (a, a) ∈ R Eg. Let A={a, b} and let R={(a, a), (a, b), (b, b)} then R is reflexive 2. Irreflexive relation (a. Ra) R is said to be irreflexive if for every element a ∈ A, a. Ra i. e. (a, a) ∉ R eg. Let A={1, 2} and let R ={(1, 2), (2, 1)}then R is irreflexive since (1, 1), (2, 2) ∉ R

eg. Let A={1, 2} and let R ={(1, 2), (2, 2)} then R is not irreflexive since (2, 2) ∈ R note: R is not reflexive either since (1, 1) ∉ R • If R is reflexive, the corresponding relation matrix(MR) will have its diagonal entries as one. • If R is irreflexive, the diagonal elements will be zero. • Diagraph of reflexive relation:

3. Symmetric relation: (a. Rb then b. Ra) R is said to be symmetric, if whenever a. Rb , then b. Ra. eg 1 Let A be the set of people let a. Rb if a is a friend of b, then obviously b is related to a , hence the relation of being friend is symmetric relation. Diagraph of symmetric relation:

4. Asymmetric relation: R is said to be asymmetric if whenever a. Rb then b. Ra. Eg. 1 Let A=R , the set of real number and let R be the relation “<“ then a<b b<a hence < is asymmetric. 5. Antisymmetric relation: (a. Rb and b. Ra then a=b) R is antisymmetric if whenever , a. Rb and b. Ra then a=b. eg Let A=R and let R be the relation “<=“ then a<=b and b<=a a=b. hence “<=“ is an antisymmetric relation.

6. Transitive relation: (a to b to c ) R is said to be transitive , if whenever a. Rb and b. Rc, then a. Rc. eg. Let A = set of triangles and let R be the relation of being congruent, then for triangle a, b, c ∈ A and a. Rb and b. Rc a. Rc. Diagraph of transitive relation

Equivalence relation • A binary relation R on a set A is called as equivalence relation if it is reflexive, symmetric and transitive. eg. 1 Let A=R and R be equality of number eg. 2 A is a set of triangles and R is similarity of triangles • Diagraph of an equivalence relation will have the following characteristics • Every vertex will have loop. • if there is an arc from a to b there should be an arc from b to a. • If there is an arc from a to b and one from b to c there should be an arc from a to c.

eg 2. Let A={a, b, c, d} R={(a, a), (b, b), (c, c), (d, d), (d, c)} determine whether R is equivalence relation? solution: R is reflexive since (a, a), (b, b), (c, c) and (d, d) ∈ R But R is not symmetric since (b, a) ∈ R but (a, b) ∉ R hence R is not an equivalence relation. eg. 3 Let A ={a, b, c} and let MR = 1 0 0 0 1 1 determine whether R is an equivalence relation?

Solution: R={(a, a), (b, b), (b, c), (c, b), (c, c)} R is reflexive since (a, a), (b, b)and (c, c) ∈ R R is symmetric since (b, c) ∈ R (c, b) ∈ R R is transitive since (b, b)and (b, c) ∈ R (b, c) and (c, b) ∈ R (b, c) and (c, c) ∈ R (b, c) ∈ R (c, b) and(b, b) ∈ R (c, b) and(b, c) ∈ R (c, c) ∈ R hence R is an equivalence relation.

• If R 1 and R 2 are equivalence relation on a set A then R 1 ᴒ R 2 is an equivalence relation • If R 1 and R 2 are equivalence relation on a set A then R 1 U R 2 is an equivalence relation Equivalence class: Let R be the equivalence relation on a set A, for every a ∈ A, let [a]R denote the set { x ∈ A |x R a} then [a]R is called as the equivalence class of a with respect to R. The rank of R is number of distinct equivalence classes of R if the number of classes is finite otherwise the rank is said to be infinite We can simply denote equivalence class as [a].

eg. 1 Let A={a, b, c} and let R={(a, a), (b, b), (c, c), (a, b), (b, a)} where R is clearly an equivalence relation find equivalence class. solution: The equivalence classes of elements of A are(element [a] is related with (a, a), (a, b)) [a]={a, b} [b]={b, a} [c]={c} The rank of R is 2

eg. 2. Let A={1, 2, 3, 4} and let R={(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (3, 1), (2, 3), (3, 2), (3, 3), (4, 4)} show that R is an equivalence relation and determine equivalence classes and hence find rank of R.

Partition(Π) • A partition of a non empty set A is a collection of sets {A 1, A 2, A 3 ------An} such that – A= i=1 UA I Ai ᴒ Aj = Φ for i not equal to j • We denote partition by Π. • An element of partition is called a block. • The rank of partition is number of blocks of Π eg. Let A={1, 2, 3} then Π 1= {{1, 2}, {3}} Π 2={{1, 3}, {2}} Π 3= {{1}, {2}, {3}}

eg. Let A={a, b, c, d}, Π ={{a, b}, {c}, {d}} find the equivalence relation induced by Π and construct its diagraph solution: R={(a, a), (a, b), (b, a), (b, b), (c, c), (d, d)} the diagraph of R is

Eg. 2 Let A ={1, 2, 3, 4, 5} and Π={{1, 2}, {3}, {4, 5}}find equivalence relation determined by Π and draw its diagraph. Solution: R ={(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 4), (4, 5), (5, 4), (5, 5)} diagraph of R

Compatible relation • A relation R on set A is said to be compatible if it is reflexive and symmetric eg. 1. All equivalence are compatible relations. eg. 2 The relation of “being friend of” is compatible relation.

Closure of relation • Depending upon nature of relations, there are 3 types of closure of relations. 1. Reflexive closure (R 1 = R U Δ) 2. Symmetric closure(R 1 = R U R-1) 3. Transitive closure(R* = R 1 U R 2 U R 3 U----- Rn) 1. Reflexive closure (R 1 = R U Δ): Let R be the relation on a set A which is not reflexive relation. A relation R 1 = R U Δ is called the reflexive closure of R if R U Δ is the smallest reflexive relation containing R. A={a, b, c, d} then Δ ={(a, a), (b, b), (c, c), (d, d)}

eg. Let A={1, 2, 3} R 1, R 2, R 3 are relations on set A. find reflexive closure of R 1, R 2, R 3. where R 1={(1, 1), (2, 1)} R 2={(1, 1), (2, 2), (3, 3)} R 3={(3, 1), (1, 3), (2, 3)} solution: we have A={1, 2, 3} therefore Δ ={(1, 1), (2, 2), (3, 3)} then i)reflexive closure of R 1 is. R=R 1 U Δ therefore R={(1, 1), (2, 2), (3, 3)} ii)The reflexive closure of R 2 is. R=R 2 U Δ therefore R={(1, 1), (2, 2), (3, 3)}

iii)The reflexive closure of R 3 is. R=R 3 U Δ therefore R={(3, 1), (1, 3), (2, 3), (1, 1), (2, 2), (3, 3)} 2. Symmetric closure(R 1 = R U R-1) Let R be the relation on a set A and R is not symmetric relation. A relation R 1= R U R-1 is called symmetric closure of R if R U R-1 is smallest symmetric relation containing R. eg. Find the symmetric closure of following relation on A={1, 2, 3} where R 1={(1, 1), (2, 1)} R 2={(1, 2), (2, 1), (3, 2)(2, 2)} R 3={(1, 1), (2, 2), (3, 3)} solution: given that A={1, 2, 3} i) R 1 -1 ={(1, 1), (1, 2)} R=R 1 U R 1 -1 R={(1, 1, ), (2, 1), (1, 2)} is a symmetric closure.

ii) R 2 -1 ={(2, 1), (1, 2), (2, 3), (2, 2)} R=R 2 U R 2 -1 R={(1, 2), (2, 1), (3, 2), (2, 3)} iii)R 3 is symmetric relation therefore R 3 itself is symmetric closure

Transitive closure(R* ) • Let R be the relation on set A which is not transitive relation. The transitive closure of a relation R is the smallest transitive relation containing R. It is denoted by R*. • Theorem: |A|=n , R be the relation on A then transitive closure (R* )= R 1 U R 2 U R 3 U----- Rn Eg. 1 If A={1, 2, 3, 4, 5} and R={(1, 2), (3, 4), (4, 5), (4, 1), (1, 1)} find its transitive closure Solution: Let R* be the transitive closure of given relation R. therefore R* = R 1 U R 2 U R 3 U R 4 U R 5 now R 2 = R. R ={(3, 5), (3, 1), (4, 2), (1, 1)} R 3 = R 2. R= {(3, 2), (3, 1), (4, 2), (4, 1), (1, 2), (1, 1)} R 4 = R 3. R= {(3, 2), (3, 1), (4, 2), (4, 1), (1, 2), (1, 1)= R 3 R 5 = R 4. R={(3, 2), (3, 1), (4, 2), (4, 1), (1, 2), (1, 1)}= R 4

therefore R* = R 1 U R 2 U R 3 U R 4 U R 5 R* ={(1, 2), (3, 4), (4, 5), (4, 1), (1, 1), (3, 5), (3, 1), (4, 2), (3, 2)} eg. 2 Let A={1, 2, 3, 4}and R ={(1, 2), (2, 3), (3, 4)} be a relation on Set A find R* and draw its diagraph.

Warshall’s Algorithm • Let S be the finite set {v 1, v 2, v 3 ------vn}, R is a relation on S. The adjacency matrix A of R is an nxn Boolean matrix defined by – Aij = 1 if the diagraph D has an edge from vi to vj. = 0 if the diagraph D has no edge from vi to vj. • Warshall’s Algorithm: It is an efficient method of finding the adjacency matrix of the transitive closure of relation R on a finite set S. It uses properties of diagraph D, in a particular walk of various lengths in D.

• Warshall’s algorithm to find transitive closure: eg 1. Find the transitive closure of the relation R on set A A={1, 2, 3, 4} defined by. R={(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (3, 4), (3, 2), (4, 3)} solution: Step 1 - we have |A|=4 thus we have to find warshall’s sets - w 0 w 1 w 2 w 3 w 4 The first set w 0 = MR = Step 2: To find w 1 from w 0 we consider the first column and first row

In C 1, 1 is present at R 2 In R 1 , 1 is present at c 2, c 3, c 4 Thus add new entries in w 1 at (R 2, C 2), (R 2, C 3), (R 2, C 4) which is given beloww 1= Step 3 - To find w 2 from w 1 we consider 2 nd column and 2 nd row In C 2 , 1 is present at R 1, R 2, R 3, R 4 In R 2 , 1 is present at C 1, C 2, C 3, C 4 thus we add new entries in w 2 at (R 1, C 1), (R 1, C 2), (R 1, C 3), (R 1, C 4), (R 2, C 1), (R 2, C 2), (R 2, C 3), (R 2, C 4), (R 3, C 1), (R 3, C 2), (R 3, C 3), (R 3, C 4), (R 4, C 1), (R 4, C 2), (R 4, C 3), (R 4, C 4) which is given below

w 2 = All entries in w 2 are 1 Hence w 2 is relation matrix of transitive closure of R and R*={(1, 1), (1, 2)(1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}

eg 2. Use warshall’s algorithm to find transitive closure of R where MR = and A={1, 2, 3}. solution: step 1 -We have|A|=3 thus we have to find warshall’s set w 0 w 1 w 2 w 3. The first set is – w 0 = MR = Step 2 –To find w 1 from w 0 we consider the first column and the first row In C 1, 1 is present at R 1, R 3. In R 1, 1 is present at C 1, C 3. thus add new entries in w 1 at (R 1, C 1), (R 1, C 3), (R 3, C 1), (R 3, C 3).

w 1 = Step 3 : To find w 2 from w 1 we consider 2 nd column and 2 nd row In R 2, 1 is present at C 2 In C 2, 1 present at R 2, R 3 thus add new entries in w 2 at (C 2, R 2), (C 2, R 3) which is given below w 2 = = w 1

Step 4: To find w 3. from w 2 we consider 3 rd column and 3 rd row In C 3, 1 is present at R 1, R 3 In R 3, 1 is present at C 1, C 2, C 3 Thus add new entries in w 3 at (R 1, C 1), (R 1, C 2), (R 1, C 3), (R 3, C 1), (R 3, C 2), (R 3, C 3) which is given below w 3 = Hence w 3 is the relation matrix of R* and R* ={{1, 1), (1, 2), (1, 3), (2, 2), (3, 1), (3, 2), (3, 3)}

eg 3. Let R ={(a, d), (b, a), (b, d), (c, b), (c, d), (d, c)} use warshall’s algorithm to find the matrix of transitive closure where A={a, b, c, d}

Partial ordering relation(POSET) • A binary relation R on a non empty set A is a partial order if R is reflexive, antisymmetric and transitive. • An ordered relation is a transitive relation on a set by means of which we can compare elements of a set. • The ordered pair (A, R) is called a partially ordered set or poset. • If the two objects are always related in a poset it is called a total order or linear order or simple order. Eg. (Z, <=) is a poset. In this case either a<=b or b<=a so two things are always related hence <= is a total order and (Z, <=) is a chain.

Hasse diagram • The poset can be represented by diagraph however more econonical way to describe poset is hasse diagram. • It is useful tool which completely describes the associated partially ordered relation. • A diagram which is drawing by considering comparable and non comparable elements is called hasse diagram. Therefore while drawing hasse diagram following points must be followed. 1. The element of a relation R are called vertices and denoted by points. 2. All loops are omited as relation is reflexive on poset.

3. If a. Rb or a<=b then join a to b by a straight line called an edge, the vertex b appears above the level of vertex a. therefore the arrows may be omitted from the edges in hasse diagram. 4. If a<= b and b<=a i. e. a and b are non comparable elements, then they lie on same level and there is no edge between a and b. 5. If a<=b and b<=c then a<=c so there is a path a b c. therefore do not join a to c directly i. e delete all edges that are implied by transitive relation.

eg. Let A ={2, 3, 4, 6} and let a. Rb if a divides b. show that R is partial order and draw its hasse diagram. solution: R={(2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)} R is reflexive since (2, 2), (3, 3), (4, 4), (6, 6) ε R, R is antisymmetric since if a. Rb , b. Ra unless a=b. R is also transitive since a. Rb and b. Rc implies a. Rc hence R is a partial order. hasse diagram for R.

eg. 2. If A={1, 2, 3, 4} R={(1, 1), (1, 2), (2, 4), (1, 3), (3, 4), (1, 4), (4, 4)} then show that R is a partial order and draw its hasse diagraph. solution: R is reflexive since (1, 1), (2, 2), (3, 3), (4, 4)εR. R is antisymmetric since (1, 2)εR but (2, 1) ∉ R. (2, 4) εR but (4, 2) ∉ R. similaraly (1, 3), (1, 4), (3, 4) εR but (3, 1), (4, 3) ∉ R. one can also similarly check that R is transitive

eg 3. Draw hasse diagram of a poset (p(s), c) where S={a, b, c}. solution: P(s)={Ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} now find the comparable and non-comparable element Ø c {a} , Ø c {b}, Ø c {c} therefore {a}, {b}, {c} lie above the level Ø. {a} c {a, b} , {b} c {b, c} , {c} c {a, c}. therefore {a, b}, {b, c}, {a, c} lie above the level of {a}, {b}, {c}. {a, b} c S , {b, c} c S {a, c} c S therefore S lie above the level of {a, b}, {a, c}, {b, c} but {a}, {b}, {c} are non comparable therefore {a}, {b}, {c} lie on same level. {a, b}, {a, c}, {b, c} are non comparable therefore lie on same level by considering the above observations the hasse diagram is


Chain and antichains • Chain: Let (A, <=) be a poset. A subset of A is called chain if every pair of elements in the subset are related. • If A iteself is a chain the poset (A, <=) is called a totally ordered set or linearly ordered set. Eg. Let A ={1, 2, 3} and let the partial order <= mean “less than or equalto” then (A, <=) is chain and its hasse diagram is • Antichain: A subset of A is called antichain if no two distinct elements in a subset are related.

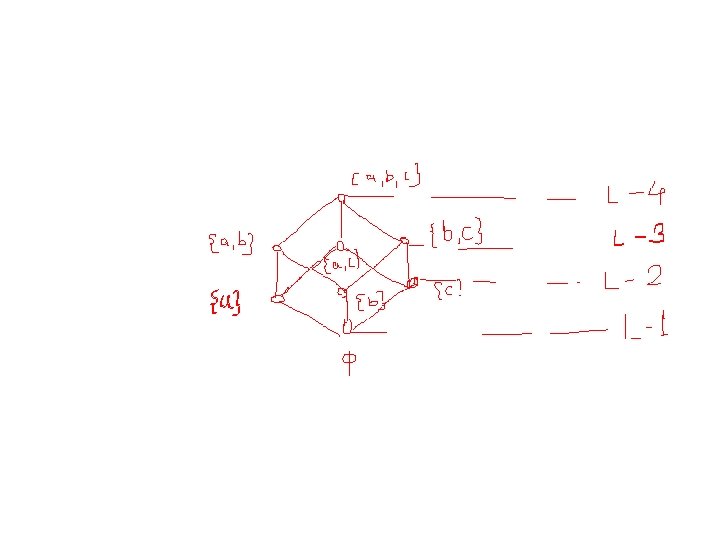
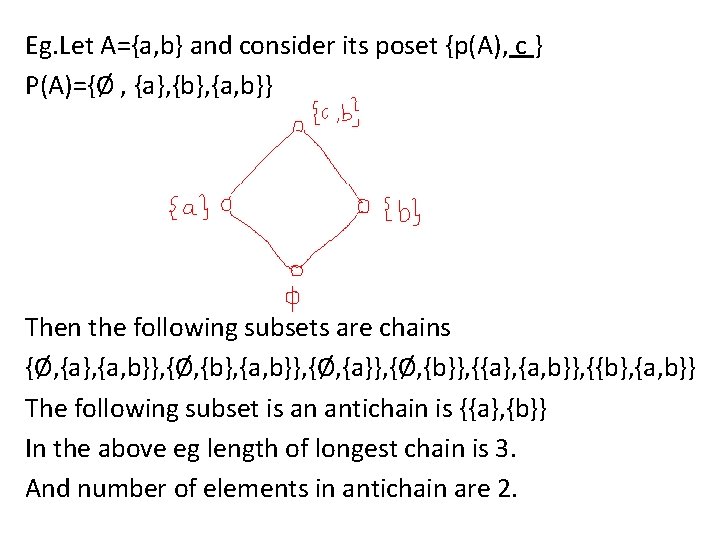
Eg. Let A={a, b} and consider its poset {p(A), c } P(A)={Ø , {a}, {b}, {a, b}} Then the following subsets are chains {Ø, {a}, {a, b}}, {Ø, {b}, {a, b}}, {Ø, {a}}, {Ø, {b}}, {{a}, {a, b}}, {{b}, {a, b}} The following subset is an antichain is {{a}, {b}} In the above eg length of longest chain is 3. And number of elements in antichain are 2.

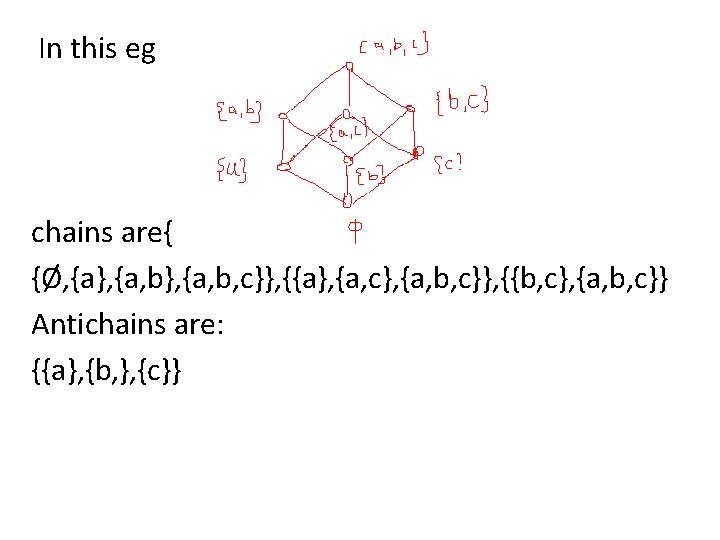
In this eg chains are{ {Ø, {a}, {a, b, c}}, {{a}, {a, c}, {a, b, c}}, {{b, c}, {a, b, c}} Antichains are: {{a}, {b, }, {c}}

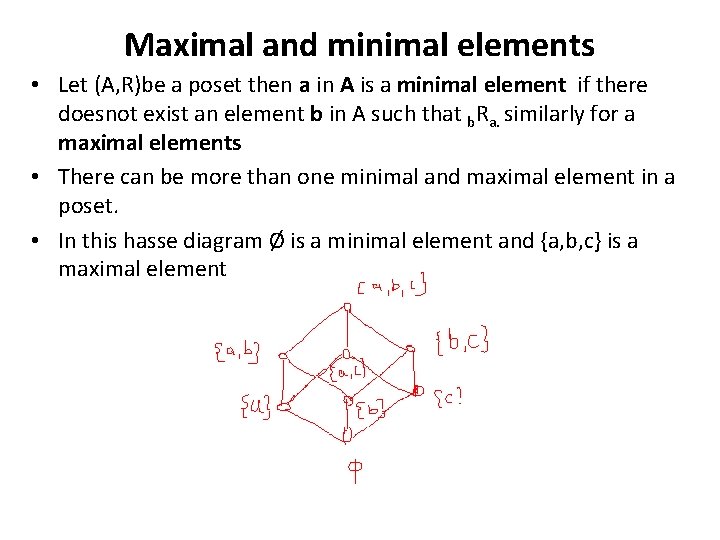
Maximal and minimal elements • Let (A, R)be a poset then a in A is a minimal element if there doesnot exist an element b in A such that b. Ra. similarly for a maximal elements • There can be more than one minimal and maximal element in a poset. • In this hasse diagram Ø is a minimal element and {a, b, c} is a maximal element

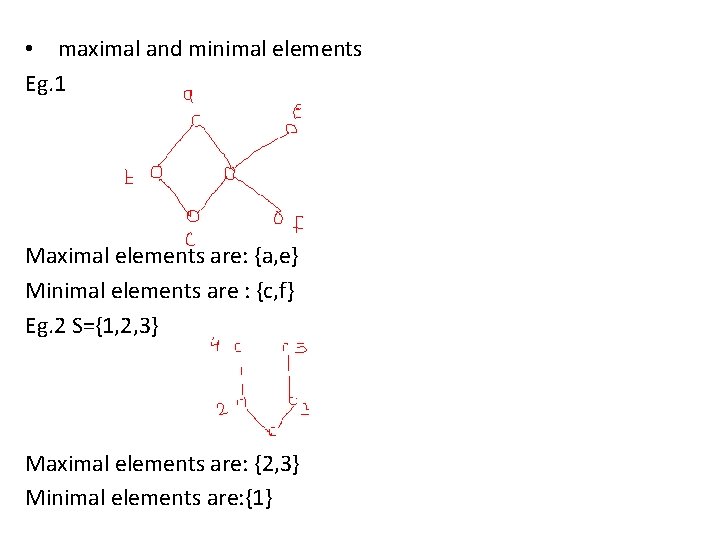
• maximal and minimal elements Eg. 1 Maximal elements are: {a, e} Minimal elements are : {c, f} Eg. 2 S={1, 2, 3} Maximal elements are: {2, 3} Minimal elements are: {1}

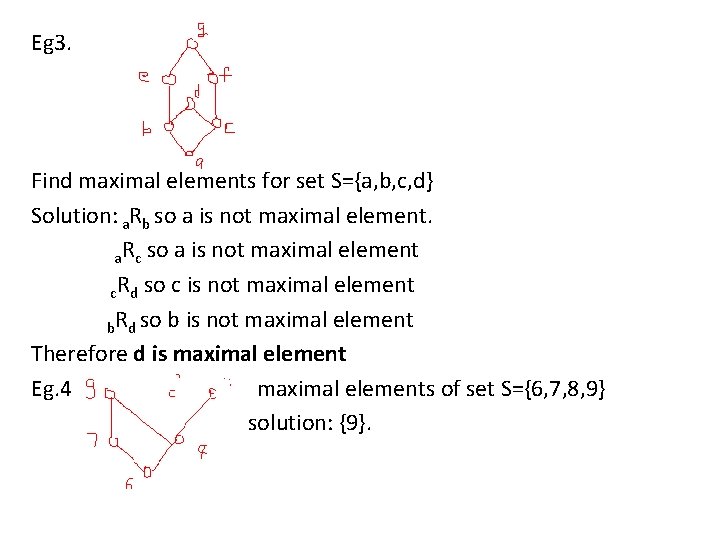
Eg 3. Find maximal elements for set S={a, b, c, d} Solution: a. Rb so a is not maximal element. a. Rc so a is not maximal element c. Rd so c is not maximal element b. Rd so b is not maximal element Therefore d is maximal element Eg. 4 maximal elements of set S={6, 7, 8, 9} solution: {9}.

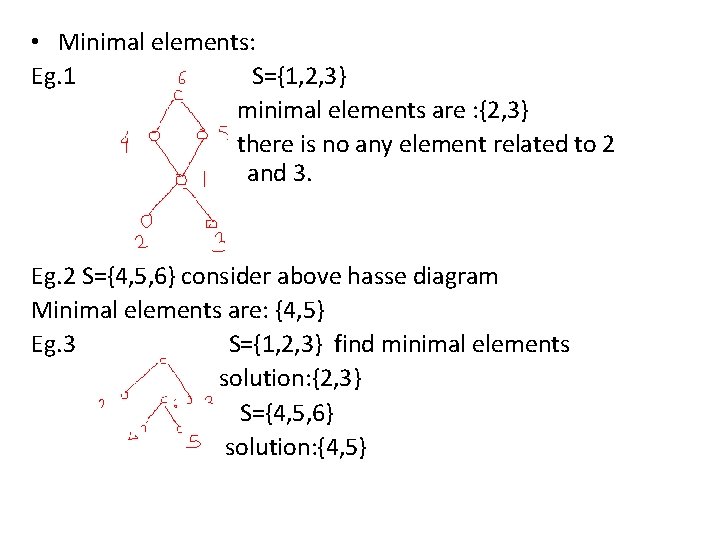
• Minimal elements: Eg. 1 S={1, 2, 3} minimal elements are : {2, 3} there is no any element related to 2 and 3. Eg. 2 S={4, 5, 6} consider above hasse diagram Minimal elements are: {4, 5} Eg. 3 S={1, 2, 3} find minimal elements solution: {2, 3} S={4, 5, 6} solution: {4, 5}

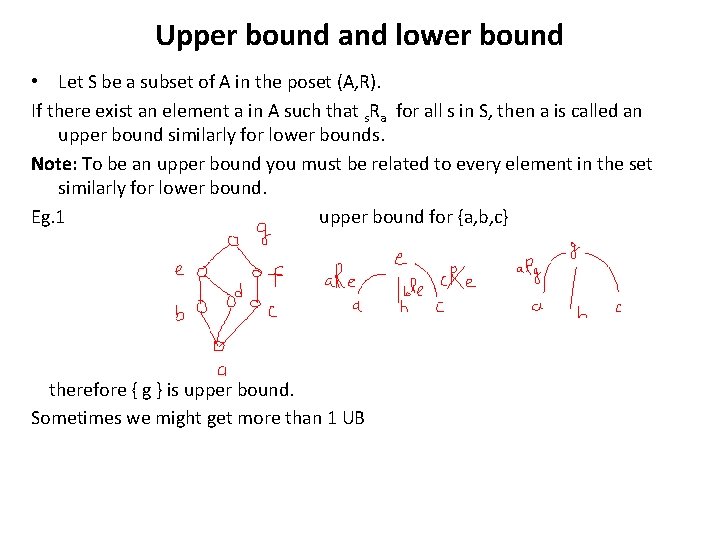
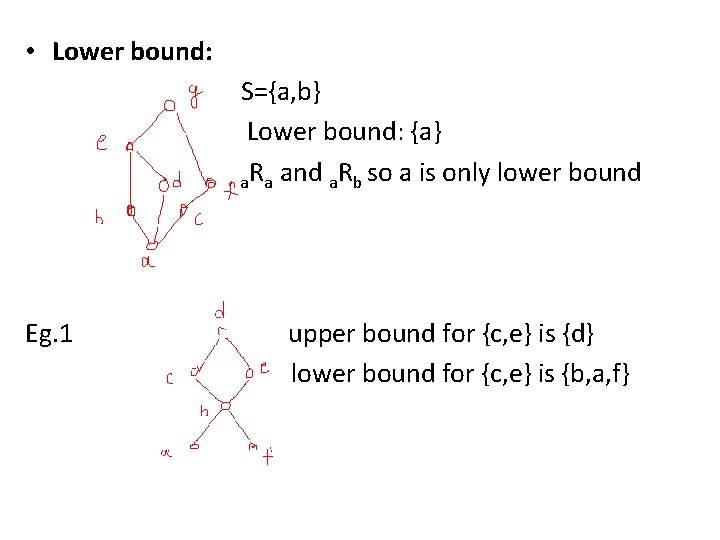
Upper bound and lower bound • Let S be a subset of A in the poset (A, R). If there exist an element a in A such that s. Ra for all s in S, then a is called an upper bound similarly for lower bounds. Note: To be an upper bound you must be related to every element in the set similarly for lower bound. Eg. 1 upper bound for {a, b, c} therefore { g } is upper bound. Sometimes we might get more than 1 UB

• Lower bound: S={a, b} Lower bound: {a} a. Ra and a. Rb so a is only lower bound Eg. 1 upper bound for {c, e} is {d} lower bound for {c, e} is {b, a, f}

Least upper bound and greatest lower bound • Let a, b be elements in a poset (A, <=) an element c is said to be an upper bound of a and b if a<=b and b<=c. • An element c is said to be a least upper bound (lub) of a and b if c is an upper bound of a and b and if there is no other upper bound d of a and b such that d<=c. • Similarly an element e is said to be a lower bound of a and b if e<=a and e<=b and e is called greatest lower bound (glb) of a and b if there is no other lower bound f of a, b such that e<=f.

Eg. 1 least upper bound(lub) of {c, e} =d greatest lower bound (glb) of {c, e}=b Upper bound of {a, f} are elements {b, c, d, e} lub{a, f}= {b} Lower bound of {a, f} : do not exist Upper bound of {b, d} is d. lub{b, d}= d lower bound for {b, d} is {b, a, f} glb{b, d}=b

Lattice • A Lattice is a poset in which every pair of elements has a least upper bound (lub)and a gretest lower bound(glb). • Let (A, <=)be a poset and a, b ε A then • lub of a & b is denoted by a v b. It is called join of a & b. i. e. a vb =lub(a, b)=join(OR). • The greatest lower bound of a and b is called the meet of a and b and it is denoted by a۸ b. therefore a۸ b = glb(a, b)=and=meet. lattice is a mathematical structure with two binary oprations v (join) and ۸ (meet) It is denoted by {L, v, ۸ }

Eg. 1 Let A={1, 2, 3}, P(A)={Ø, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} show that (P(A), c ) is a lattice Solution: The hasse diagram of the poset (P(A), c ) is Here every pair of elements of a poset has lub and glb hence (P(A), c ) is a lattice.

Eg 2. Determine which of the following posets are lattice In figure every pair of elements has lub and glb. It is a lattice. Eg. 3 Every pair of element has lub and glb. It is a lattice

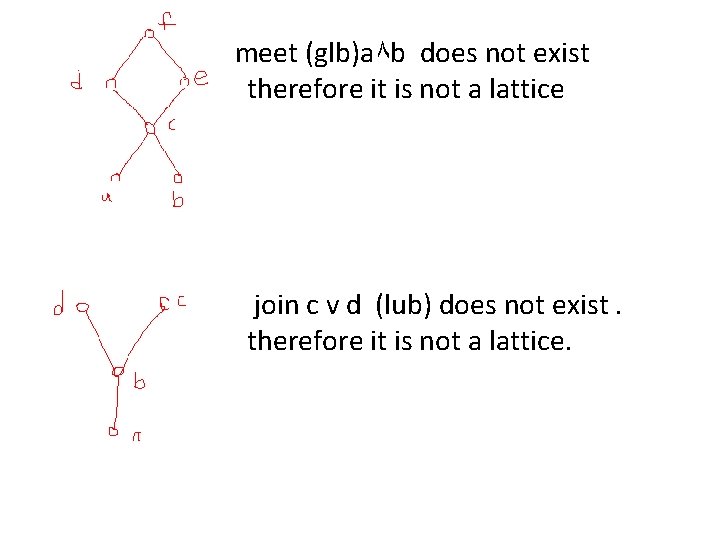
meet (glb)a۸ b does not exist therefore it is not a lattice join c v d (lub) does not exist. therefore it is not a lattice.

Properties of lattice • Let (L, ۸ , v) be a lattice and a, b, c ∉ L then L satisfies the following properties. 1. Commutative property: a۸ b=b ۸ a and avb =bva 2. Associative property: av(b۸ c)= (avb)۸ (avc) a۸ (bvc)=(a۸ b)v(a۸ c) 3. Absorption law: a۸ (a v b)=(a۸ a )v (a۸ b)=a a۸ a = a , ava =a a۸ b=a iff avb =b

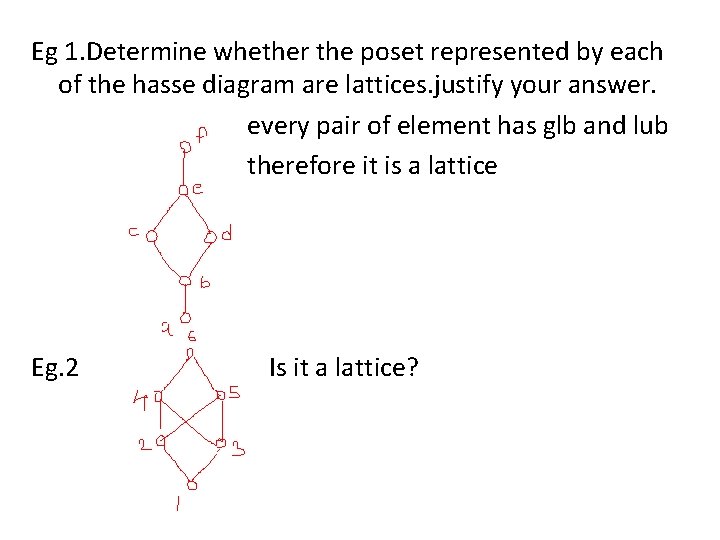
Eg 1. Determine whether the poset represented by each of the hasse diagram are lattices. justify your answer. every pair of element has glb and lub therefore it is a lattice Eg. 2 Is it a lattice?

Eg 3 Let A be the set of positive factors of 15 and R be a relation on A. R={ x. Ry |x divides y, x, y ∈ A} Draw hasse diagram and give meet and join for lattice. Solution: we have A={1, 3, 5, 15} R={(1, 1), (1, 3), (1, 5), (1, 15), (3, 15), (5, 15), (15, 15)} Hasse diagram- Every pair of element has lub and glb. therefore it is a lattice.

Function • Let A and B be the non empty set. A function “f” from A to B, denoted as f : A B , is a relation from A to B such that for every a ε A, there exists a unique b ε B such that (a, b) ε f. • Normally if (a, b) ε f , we write f(a)=b. • f is a relation with following property If f(a)=b and f(a)=c then a=c f: A B, it is read as f is a function of A to B. • Set A is known as Domain of f. • Set B is known as co-domain of f. • In function one to many relation is not allowed.

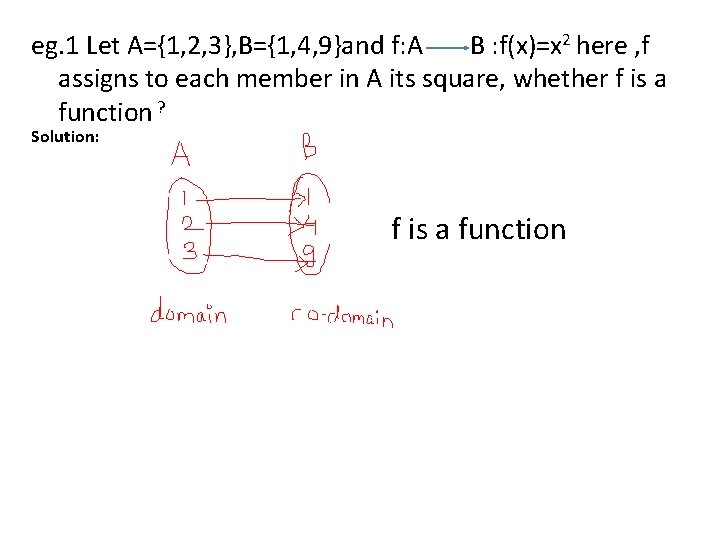
eg. 1 Let A={1, 2, 3}, B={1, 4, 9}and f: A B : f(x)=x 2 here , f assigns to each member in A its square, whether f is a function ? Solution: f is a function

eg. 2 Let A ={a, b, c} and B={1, 2, 3} then f={(a, 1), (b, 2), (a, 3), (c, 3)}. Solution: It is not a function from A to B as two elements 1 and 3 ε B are assigned to the same element a ε A It is not a function as a is mapped with 1 as well as 3

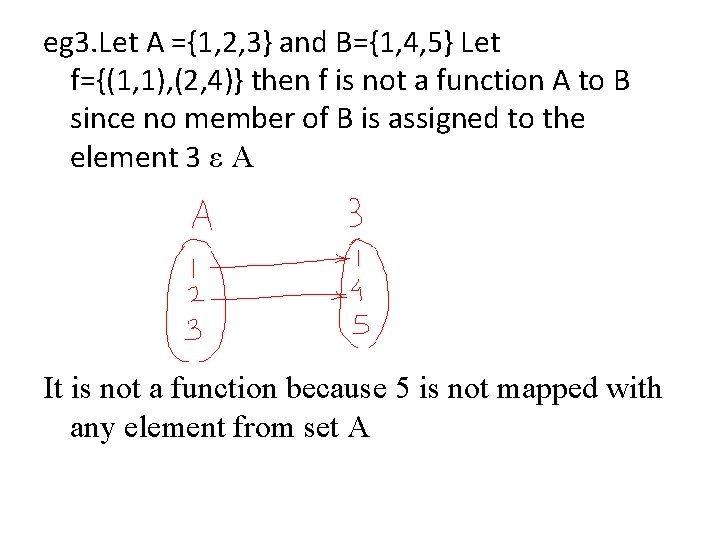
eg 3. Let A ={1, 2, 3} and B={1, 4, 5} Let f={(1, 1), (2, 4)} then f is not a function A to B since no member of B is assigned to the element 3 ε A It is not a function because 5 is not mapped with any element from set A

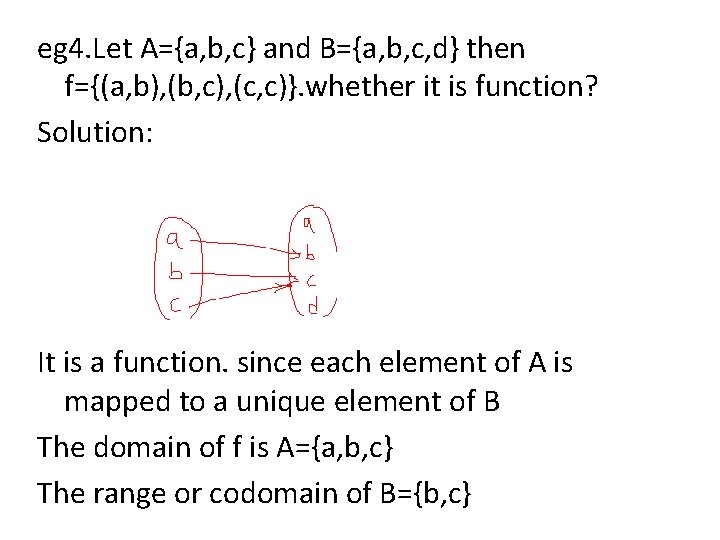
eg 4. Let A={a, b, c} and B={a, b, c, d} then f={(a, b), (b, c), (c, c)}. whether it is function?

eg 4. Let A={a, b, c} and B={a, b, c, d} then f={(a, b), (b, c), (c, c)}. whether it is function? Solution: It is a function. since each element of A is mapped to a unique element of B The domain of f is A={a, b, c} The range or codomain of B={b, c}

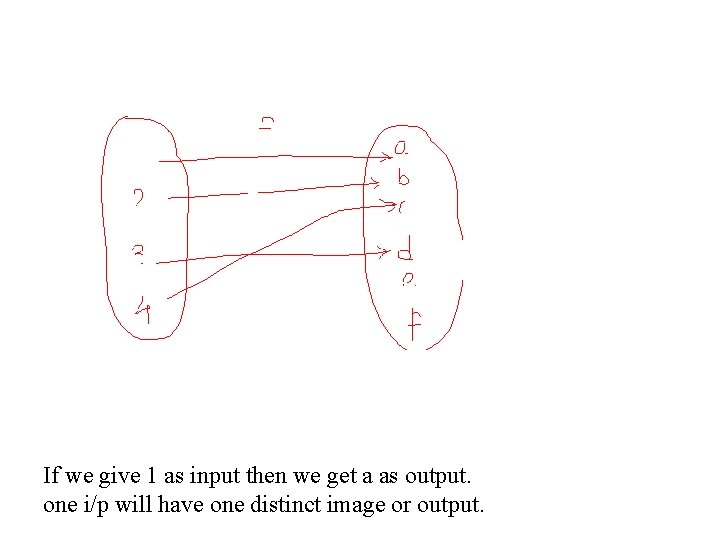
Types of functions • One-one (Injective) • onto(surjective) • one-one and onto(bijective) 1. one-one(injective): A function f : X Y is defined to be one –one or injective , if the images of distinct elements of X under f are distinct, i. e. for every x 1, x 2 ε X, f(x 1)=f(x 2) implies x 1=x 2, otherwise many one.

If we give 1 as input then we get a as output. one i/p will have one distinct image or output.

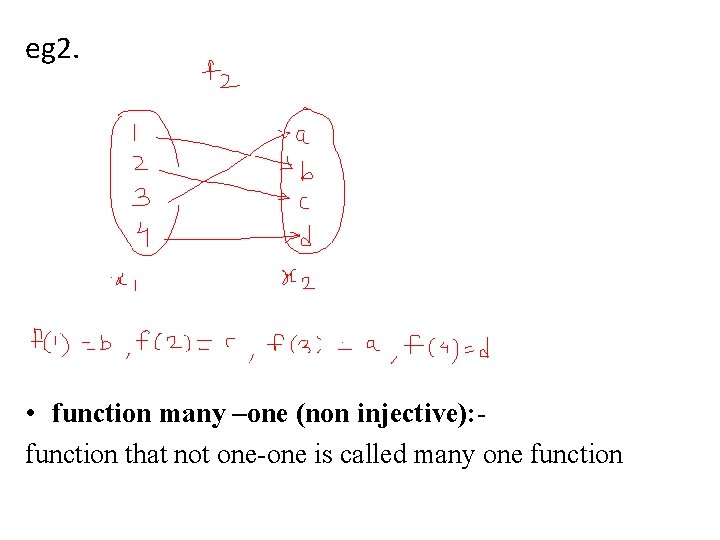
eg 2. • function many –one (non injective): function that not one-one is called many one function

• outputs are not distinct , there are 2 values 1 &2 share the same o/p. • therefore function is many one or non injective

2. onto (surjective): A function f: X Y is said to be onto(surjective) if every element of Y is the image of some element of X under f, that is for every y ε Y, there exists an element x in Xsuch that f(x)=y Every co-domain element is mapped and every element in codomain has preimage so it is onto function

Every co-domain element is mapped and every element in codomain has preimage so it is onto function

3. one-one and onto(bijective): A function f: A B is said to be bijective if f is both injective and surjective. • In other words , a function f: A B is a bijection if 1. It is one-one i. e f(x)=f(y) x=y for all x, y ε A. 2. It is onto i. e. for all y ε B there exists x εA , such that f(x)=y • If function is 1: 1 and onto then it is having special meaning i. e invetible function.

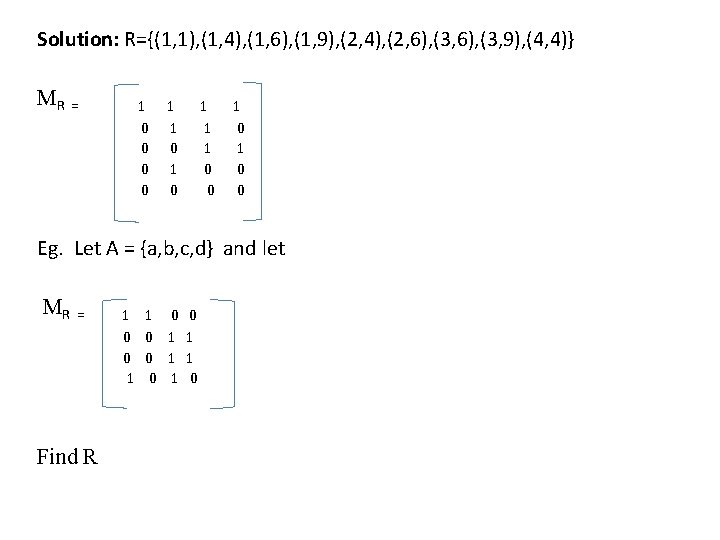
Composite function or product of function • Let f: A B & g: B C be two functions. The composite function of f and g denoted by gof : A C is a function such that gof(a)=g[f(a)] =g[b] • domain of gof is set A and codomain of gof is set B eg. 1 Let f(x)=x+2, g(x)=x-2 find i) gof ii)fog iii)gog iv) fof [May 08, Dec 12 4 M] solution: f(x)=x+2 g(x)=x-2
![i gof solution gofxgfx gx2 x2 2 x ii fog solution fgx fx2 i) gof solution: gof(x)=g[f(x)] =g[x+2] =x+2 -2 =x ii) fog solution: f[g(x)] =f[x-2] =](https://slidetodoc.com/presentation_image_h/8a66645ac8ba0c1a1af07d91bf3a5844/image-100.jpg)
i) gof solution: gof(x)=g[f(x)] =g[x+2] =x+2 -2 =x ii) fog solution: f[g(x)] =f[x-2] = x-2+2 =x
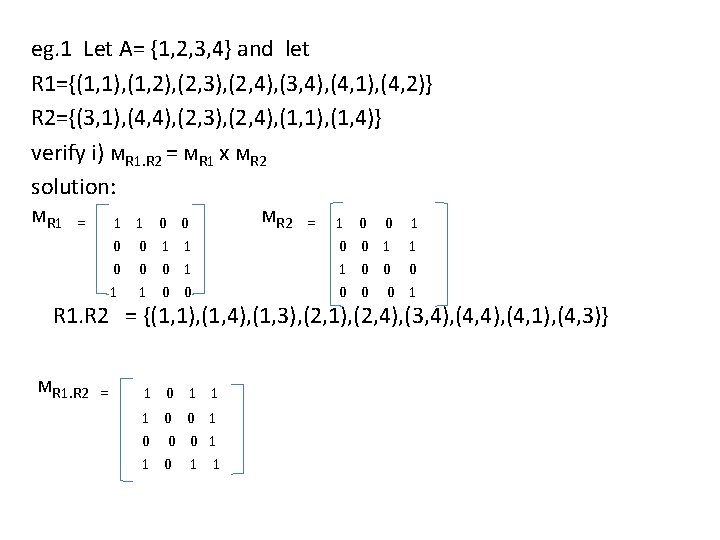
![iii gog solution gogx gx2 x2 2 x4 iv fof solution fofx fx2 iii) gog solution: gog(x) =g[x-2] =x-2 -2 =x-4 iv) fof solution: fof(x) = f[x+2]](https://slidetodoc.com/presentation_image_h/8a66645ac8ba0c1a1af07d91bf3a5844/image-101.jpg)
iii) gog solution: gog(x) =g[x-2] =x-2 -2 =x-4 iv) fof solution: fof(x) = f[x+2] =x+2+2 =x+4
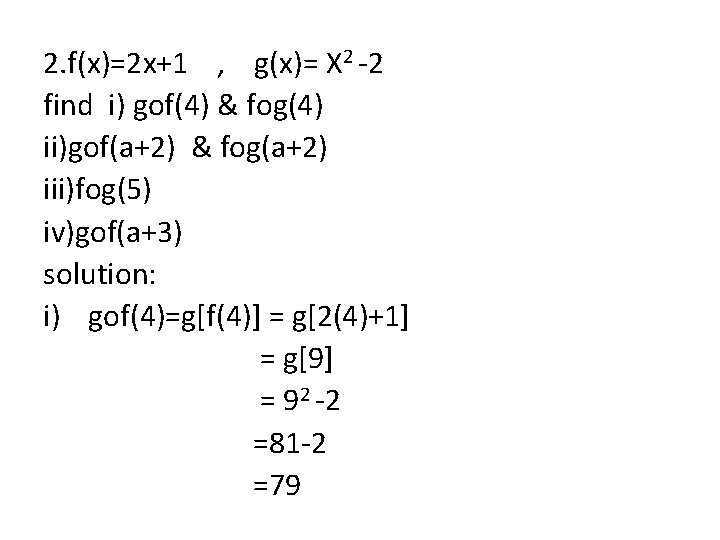
2. f(x)=2 x+1 , g(x)= X 2 -2 find i) gof(4) & fog(4) ii)gof(a+2) & fog(a+2) iii)fog(5) iv)gof(a+3) solution: i) gof(4)=g[f(4)] = g[2(4)+1] = g[9] = 92 -2 =81 -2 =79

Q-1. Given a relation whether it is a function Q-2. How many function possible from set A to B Q 2. the number of function from set A to B where |A|=m, |B|=n? The number of tasks available T 1 is mapped with a 1. T 2 will mapped with a 2 and so on. a 1 can be mapped with any value of B same with a 2, a 3 --am. The task a 1 can be mapped with m ways.

therefore Ta 1 =n ways, Ta 2 =n ways -----nm times. Tf = Ta 1 Ta 2 Tam | Tf |=| Ta 1| |Ta 2 | | Tam | = nxnxn------m times = nm eg 1. f(x)= x 2 is it a function? solution: x is mapping with x 2 i. e. x x 2 random number we take it will mapped with random number. 2 4 3 9 4 16 every number has single image. therefore it is a function

eg 2. f(x) = is it a function? domain is real solution: x mapped with every element is mapped with exactly one element R mapped with where R is real number 4 mapped with +2 or -2 therefore element have multiple images it is not real number , it is imaginary number. therefore it is not a function

How to check it is one to one function or not • image of x 1 = image of x 2 therefore f(x 1)=f(x 2) then x 1=x 2 eg 1. f(x)= X 2 is it one to one or not? R implies R(real no) Solution: f(x 1)=f(x 2) x 12 =x 2 2 = ( x 12 - x 2 2 )= 0 ( x 1 - x 2) (x 1+ x 2)=0 x 1 = x 2 or x 1 = - x 2 but we have to prove x 1=x 2 , but here another case is present so it is not one to one.
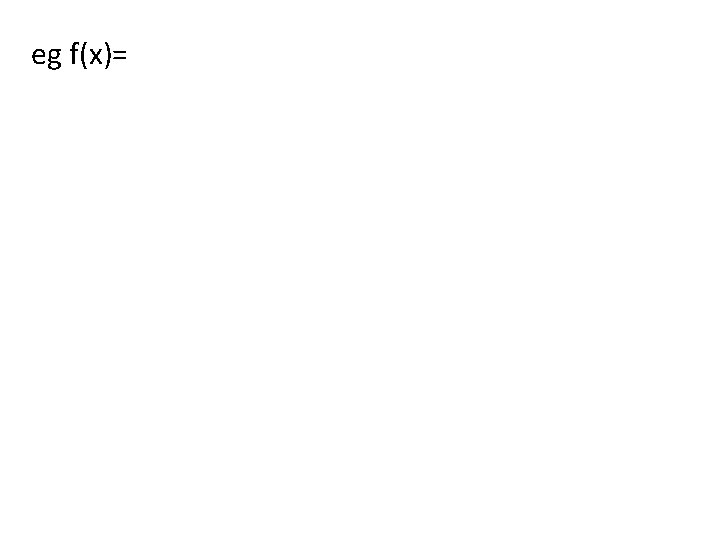
eg f(x)=

Pigeonhole principle

 Unit 5 lesson 6 formalizing relations and functions
Unit 5 lesson 6 formalizing relations and functions Unit 5 lesson 6 formalizing relations and functions
Unit 5 lesson 6 formalizing relations and functions Employee relations in public relations
Employee relations in public relations Relations and functions
Relations and functions 1-2 practice analyzing graphs of functions and relations
1-2 practice analyzing graphs of functions and relations Horizontal line test
Horizontal line test Linear relations and functions
Linear relations and functions Inverse functions notes
Inverse functions notes 6-7 inverse relations and functions
6-7 inverse relations and functions Lesson 5-2 inverses of functions
Lesson 5-2 inverses of functions 4-2 inverses of relations and functions
4-2 inverses of relations and functions 1-2 analyzing graphs of functions and relations
1-2 analyzing graphs of functions and relations 4-2 practice b inverses of relations and functions
4-2 practice b inverses of relations and functions Relations and functions equations
Relations and functions equations Analyzing graphs of functions
Analyzing graphs of functions Implicitly defined
Implicitly defined Relation vs function
Relation vs function 1-7 inverse relations and functions
1-7 inverse relations and functions Inverse relations and functions
Inverse relations and functions Function vs not a function
Function vs not a function Characteristics of relations and functions
Characteristics of relations and functions Topic 1 relations and functions
Topic 1 relations and functions Linear relations and functions
Linear relations and functions Inverse composition rule
Inverse composition rule Function vs relation
Function vs relation Unit 10, unit 10 review tests, unit 10 general test
Unit 10, unit 10 review tests, unit 10 general test Organisatuer textuel
Organisatuer textuel Emerging challenges of industrial relations in india
Emerging challenges of industrial relations in india Introduction aux relations internationales s1
Introduction aux relations internationales s1 How to evaluate function
How to evaluate function Evaluating functions and operations on functions
Evaluating functions and operations on functions Unit 8 review logarithms
Unit 8 review logarithms Examples of exponential equations
Examples of exponential equations Horizontal asymptotes rules
Horizontal asymptotes rules Algebra 2 unit 6 radical functions quiz 6-1 answers
Algebra 2 unit 6 radical functions quiz 6-1 answers Factoring patterns
Factoring patterns Unit circle
Unit circle Radical functions and rational exponents unit test
Radical functions and rational exponents unit test Absolute value piecewise function
Absolute value piecewise function Unit 1 introduction names and terms to know
Unit 1 introduction names and terms to know Unit 1 introduction to law and the legal system
Unit 1 introduction to law and the legal system Right triangle trigonometry examples
Right triangle trigonometry examples Unit process and unit operation
Unit process and unit operation Difference between unit process and unit operation
Difference between unit process and unit operation Introduction to quadratic functions
Introduction to quadratic functions Piecewise function generator
Piecewise function generator Asymptote rules
Asymptote rules Quiz 2-3 parent functions transformations graphing
Quiz 2-3 parent functions transformations graphing Introduction to functions (review game)
Introduction to functions (review game) Section 3 introduction to functions
Section 3 introduction to functions Parent function algebra
Parent function algebra Introduction to logarithmic functions
Introduction to logarithmic functions Relation between pressure and kinetic energy of gas
Relation between pressure and kinetic energy of gas Transistor ie=ib+ic
Transistor ie=ib+ic Usp solubility
Usp solubility Relation between ac and mc in economics
Relation between ac and mc in economics Bank and customer relation
Bank and customer relation Relationship between political science and economics
Relationship between political science and economics Angular quantities and linear quantities cannot be related.
Angular quantities and linear quantities cannot be related. Relation between electric field and potential
Relation between electric field and potential Intensity of pressure definition
Intensity of pressure definition Relation between sociology and political science
Relation between sociology and political science Political science and history relationship
Political science and history relationship Realeff effect in complete denture
Realeff effect in complete denture Gear wheel
Gear wheel Cylindrical coordinate grapher
Cylindrical coordinate grapher Relationship between current and capacitance
Relationship between current and capacitance Torque and slip relation
Torque and slip relation Relationship between banker and customer
Relationship between banker and customer Magnetic moment and magnetic field relation
Magnetic moment and magnetic field relation Shear and moment diagram graphical method
Shear and moment diagram graphical method Relationship between banker and customer
Relationship between banker and customer Case bank
Case bank Relation and function
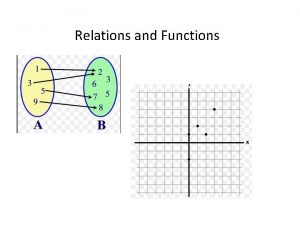
Relation and function Relation and function
Relation and function Relation between marginal utility and total utility
Relation between marginal utility and total utility Heel and toe arrangement in carding
Heel and toe arrangement in carding Quality and cost relationship
Quality and cost relationship Mathematical relationship between temperature and pressure
Mathematical relationship between temperature and pressure The expression is a
The expression is a Relation between temperature and pressure
Relation between temperature and pressure Relation between mean median and mode
Relation between mean median and mode Relationship between force and momentum
Relationship between force and momentum What is a branch in electrical circuit
What is a branch in electrical circuit What is the range of the relation
What is the range of the relation Green's theorem direction
Green's theorem direction Function or not
Function or not Uncertainty relation and natural line width
Uncertainty relation and natural line width Relation between fourier and laplace transform
Relation between fourier and laplace transform Complex refractive index
Complex refractive index Factors and multiples puzzle
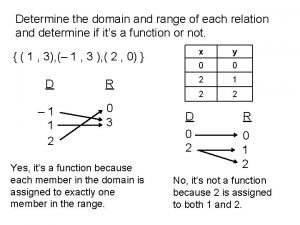
Factors and multiples puzzle Domain and range of each relation
Domain and range of each relation Current and inductance relationship
Current and inductance relationship Relation between irms and imax
Relation between irms and imax Frequency and wavelength relation
Frequency and wavelength relation How to convert rms to peak
How to convert rms to peak Impulse momentum relationship
Impulse momentum relationship Voltage and capacitance relationship
Voltage and capacitance relationship Electric potential to work
Electric potential to work Relationship between heat and energy
Relationship between heat and energy Relationship between work and energy
Relationship between work and energy Connection between language and thought
Connection between language and thought Copper chloride fire
Copper chloride fire Lambda formula
Lambda formula Vibrational partition function
Vibrational partition function Partition function in statistical mechanics
Partition function in statistical mechanics Relation between wavelength and frequency
Relation between wavelength and frequency Unit 8 rational functions homework 1
Unit 8 rational functions homework 1 Radical and rational functions
Radical and rational functions Unit 5 polynomial functions homework 1
Unit 5 polynomial functions homework 1