Gradient Methods Yaron Lipman May 2003 Preview l


































- Slides: 42

Gradient Methods Yaron Lipman May 2003

Preview l l l Background Steepest Descent Conjugate Gradient

Preview l l l Background Steepest Descent Conjugate Gradient

Background l l l Motivation The gradient notion The Wolfe Theorems

Motivation l The min(max) problem: l But we learned in calculus how to solve that kind of question!

Motivation l l Not exactly, Functions: High order polynomials: What about function that don’t have an analytic presentation: “Black Box”

Motivation l “real world” problem finding harmonic mapping l General problem: find global min(max) This lecture will concentrate on finding local minimum. l

Background l l l Motivation The gradient notion The Wolfe Theorems


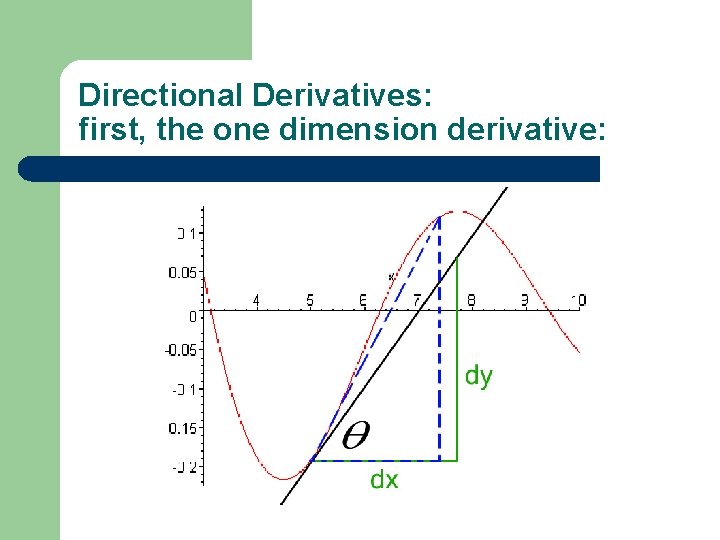
Directional Derivatives: first, the one dimension derivative:

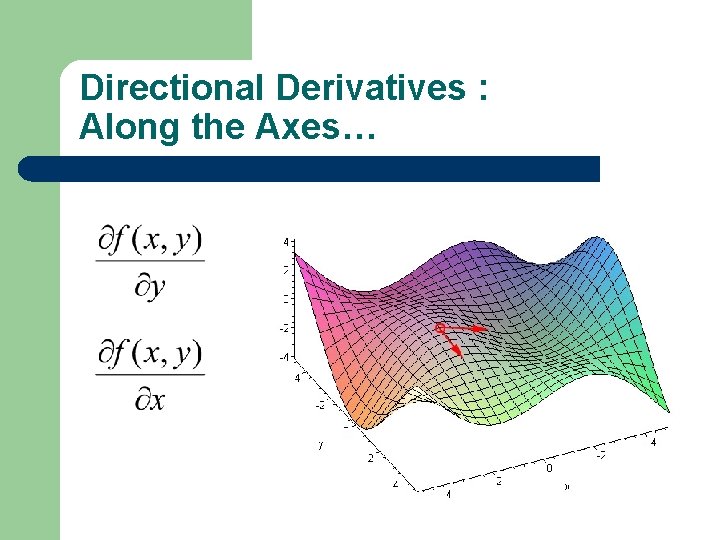
Directional Derivatives : Along the Axes…

Directional Derivatives : In general direction…

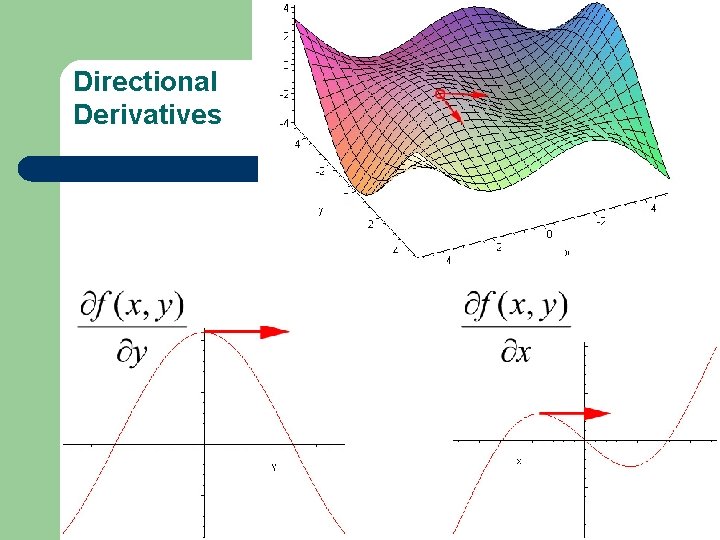
Directional Derivatives

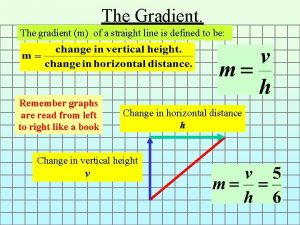
The Gradient: Definition in In the plane

The Gradient: Definition

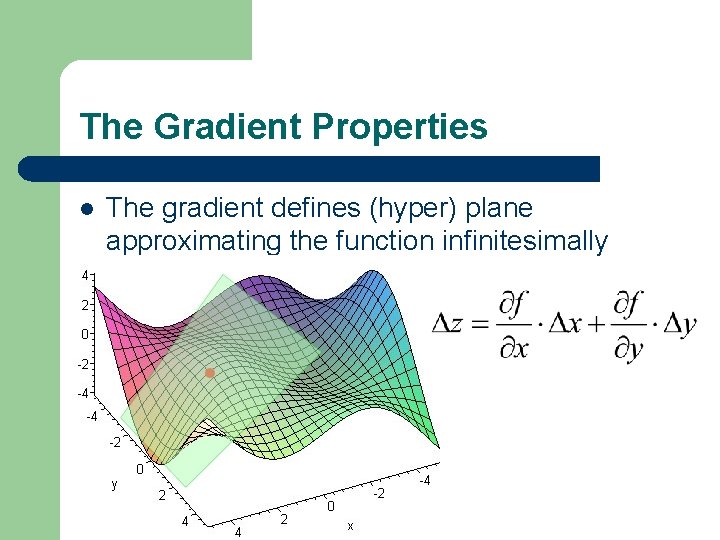
The Gradient Properties l The gradient defines (hyper) plane approximating the function infinitesimally

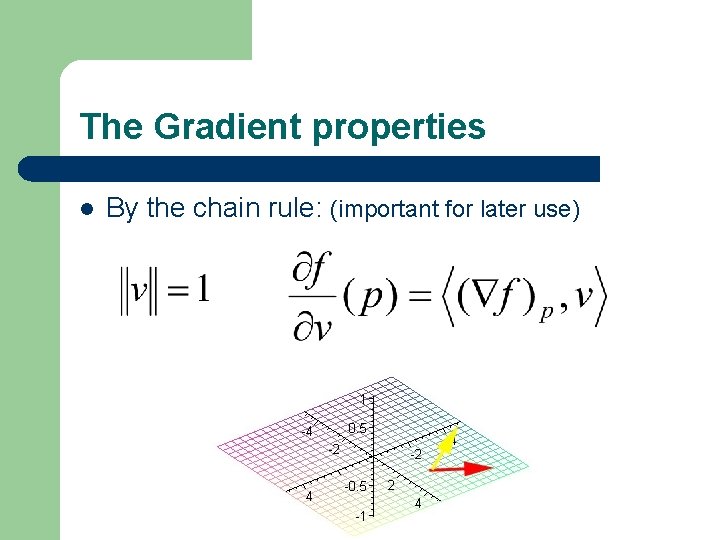
The Gradient properties l By the chain rule: (important for later use)

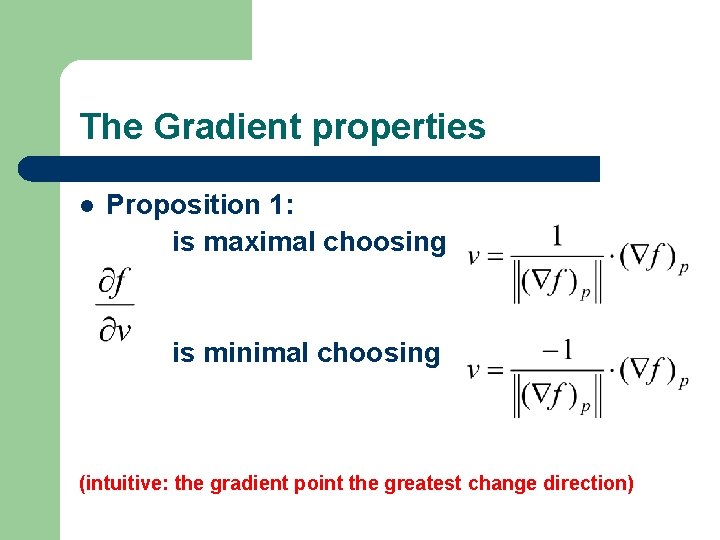
The Gradient properties l Proposition 1: is maximal choosing is minimal choosing (intuitive: the gradient point the greatest change direction)

The Gradient properties Proof: (only for minimum case) Assign: by chain rule:

The Gradient properties On the other hand for general v:

The Gradient Properties l Proposition 2: let be a smooth function around P, if f has local minimum (maximum) at p then, (Intuitive: necessary for local min(max))

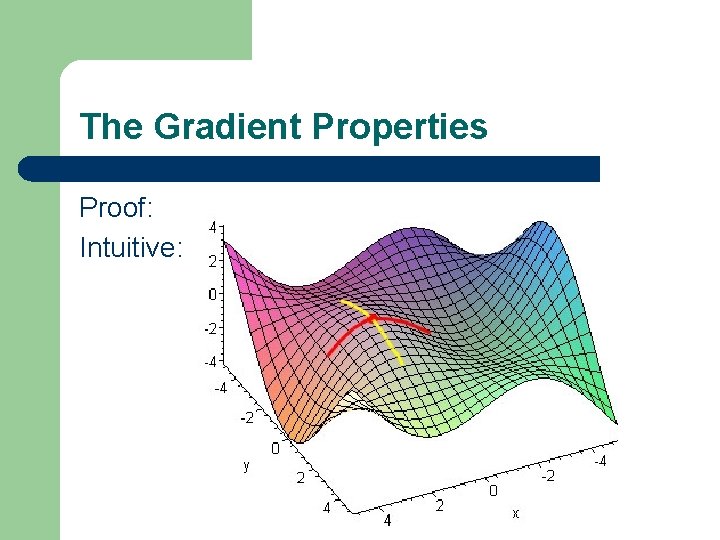
The Gradient Properties Proof: Intuitive:

The Gradient Properties Formally: for any We get:

The Gradient Properties l l l We found the best INFINITESIMAL DIRECTION at each point, Looking for minimum: “blind man” procedure How can we derive the way to the minimum using this knowledge?

Background l l l Motivation The gradient notion The Wolfe Theorems

The Wolfe Theorem l l This is the link from the previous gradient properties to the constructive algorithm. The problem:

The Wolfe Theorem We introduce a model for algorithm: Data: Step 0: set i=0 Step 1: if stop, else, compute search direction Step 2: compute the step-size l Step 3: set go to step 1

The Wolfe Theorem: suppose smooth, and exist continuous function: C 1 And, the search vectors constructed by the model algorithm satisfy:

The Wolfe Theorem And Then if is the sequence constructed by the algorithm model, then any accumulation point y of this sequence satisfy:

The Wolfe Theorem The theorem has very intuitive interpretation : Always go in decent direction.

Preview l l l Background Steepest Descent Conjugate Gradient

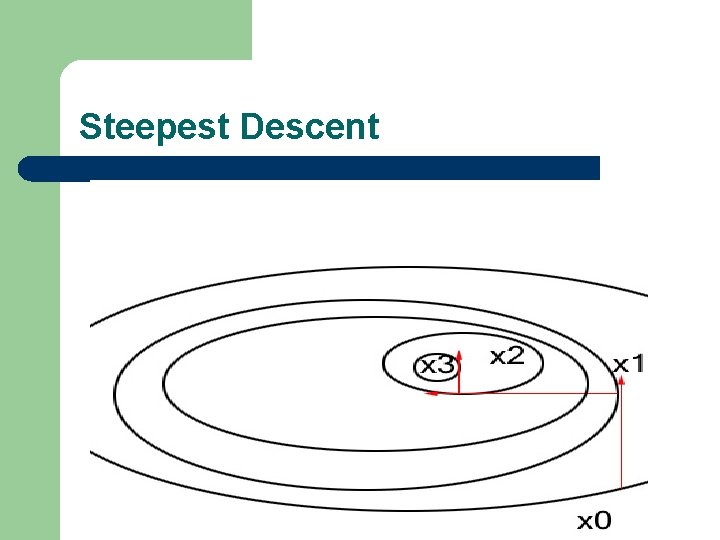
Steepest Descent l l What it mean? We now use what we have learned to implement the most basic minimization technique. First we introduce the algorithm, which is a version of the model algorithm. The problem:

Steepest Descent Steepest descent algorithm: Data: Step 0: set i=0 Step 1: if stop, else, compute search direction Step 2: compute the step-size l Step 3: set go to step 1

Steepest Descent l Theorem: if is a sequence constructed by the SD algorithm, then every accumulation point y of the sequence satisfy: Proof: from Wolfe theorem

Steepest Descent l From the chain rule: l Therefore the method of steepest descent looks like this:

Steepest Descent

Steepest Descent l l The steepest descent find critical point and local minimum. Implicit step-size rule Actually we reduced the problem to finding minimum: There are extensions that gives the step size rule in discrete sense. (Armijo)

Preview l l l Background Steepest Descent Conjugate Gradient

Conjugate Gradient l l Modern optimization methods : “conjugate direction” methods. A method to solve quadratic function minimization: (H is symmetric and positive definite)

Conjugate Gradient l Originally aimed to solve linear problems: l Later extended to general functions under rational of quadratic approximation to a function is quite accurate.

Conjugate Gradient l l l The basic idea: decompose the n-dimensional quadratic problem into n problems of 1 dimension This is done by exploring the function in “conjugate directions”. Definition: H-conjugate vectors:

Conjugate Gradient l If there is an H-conjugate basis then: l N problems in 1 -dimension (simple smiling quadratic) The global minimizer is calculated sequentially starting from x 0: l
 2017 apush exam
2017 apush exam Chap lipman
Chap lipman Yaron ernst
Yaron ernst Yaron shohat
Yaron shohat Disadvantages of realistic job preview
Disadvantages of realistic job preview Sccm technical preview
Sccm technical preview Verbal intercultural communication
Verbal intercultural communication Skimming newspaper
Skimming newspaper The selection preview
The selection preview Nnn preview
Nnn preview Tams sat score
Tams sat score Test prep preview
Test prep preview Line between pada perintah column digunakan untuk membuat
Line between pada perintah column digunakan untuk membuat Preview statement speech example
Preview statement speech example Nnn image preview
Nnn image preview 1984 book preview
1984 book preview Thesis examples
Thesis examples Test prep preview
Test prep preview Test prep preview
Test prep preview Preview of main points
Preview of main points Review and preview
Review and preview Classic trio' of selection techniques
Classic trio' of selection techniques What is a preview statement
What is a preview statement Menu collections pane di windows movie maker berguna untuk
Menu collections pane di windows movie maker berguna untuk Yandex.ru video
Yandex.ru video Thesis and preview statement example
Thesis and preview statement example The four agreements preview
The four agreements preview Test prep preview
Test prep preview Preview speech
Preview speech Benefits of hr forecasting
Benefits of hr forecasting Test prep preview
Test prep preview Test prep preview
Test prep preview Nút lệnh print preview nằm ở đâu
Nút lệnh print preview nằm ở đâu Test prep preview
Test prep preview Test prep preview
Test prep preview A-wax pattern recognition
A-wax pattern recognition Hci patterns
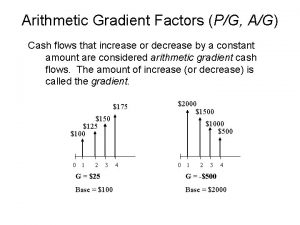
Hci patterns Arithmetic gradient formula
Arithmetic gradient formula Boardworks ltd 2011
Boardworks ltd 2011 Normal abg values
Normal abg values Coriolis force
Coriolis force Vector calculus examples
Vector calculus examples Vanishing gradient
Vanishing gradient