Goodness of Fit Test 1 State the null

Goodness of Fit Test 1. State the null and alternative hypotheses. 2. Select a random sample and record observed frequency fi for the ith category (k categories). 3. Compute expected frequency ei for the ith category: 4. Compute the value of the test statistic. if ei > 5, this has a chi-square distribution 5. Reject H 0 if df = k – 1

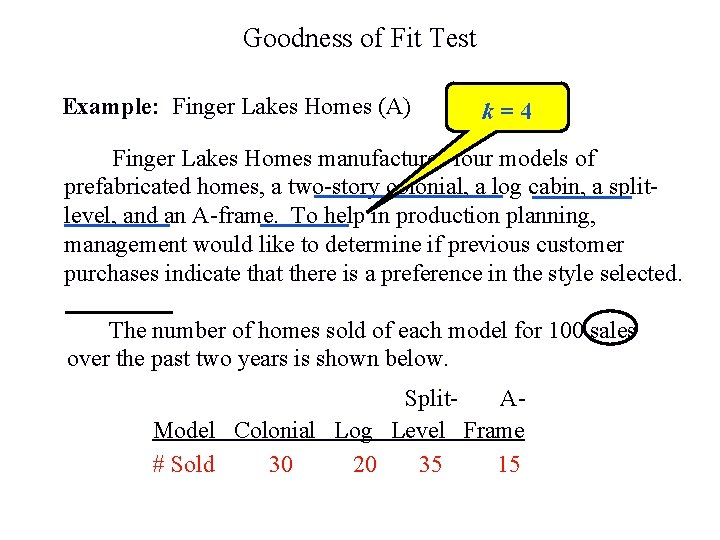
Goodness of Fit Test Example: Finger Lakes Homes (A) k=4 Finger Lakes Homes manufactures four models of prefabricated homes, a two-story colonial, a log cabin, a splitlevel, and an A-frame. To help in production planning, management would like to determine if previous customer purchases indicate that there is a preference in the style selected. The number of homes sold of each model for 100 sales over the past two years is shown below. Split. AModel Colonial Log Level Frame # Sold 30 20 35 15

Goodness of Fit Test ei = (n)(pi) Hypotheses 1/4 H 0: p. C = p. L = p. S = p. A =. 25 Ha: customers prefer a particular style i. e. , there is at least one proportion much greater than. 25 Expected frequencies e 1 = (0. 25)(100) = 25 e 2 = (0. 25)(100) = 25 e 3 = (0. 25)(100) = 25 e 4 = (0. 25)(100) = 25

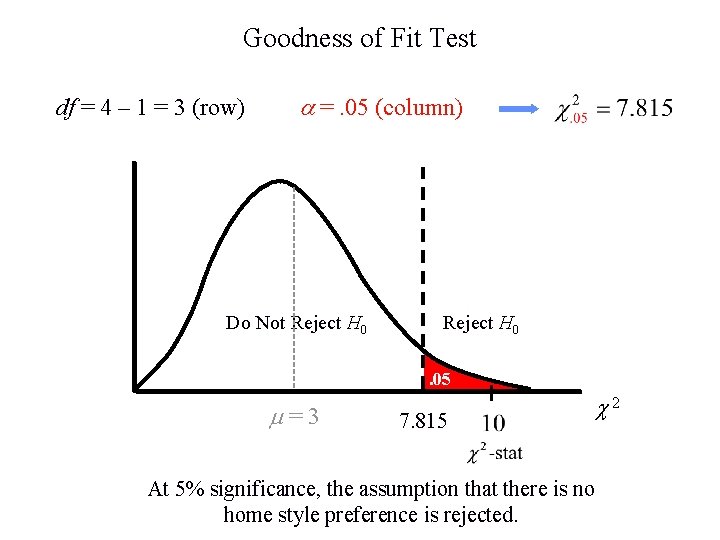
Goodness of Fit Test df = 4 – 1 = 3 (row) =. 05 (column) Do Not Reject H 0. 05 =3 7. 815 At 5% significance, the assumption that there is no home style preference is rejected. 2

Independence Test 1. State the null and alternative hypotheses. 2. Select a random sample and record observed frequency fi for each cell of the contingency table. 3. Compute expected frequency eij for each cell 4. Compute the test statistic. if ei > 5, this has a chi-square distribution 5. Reject H 0 if df = (m - 1)(k - 1)

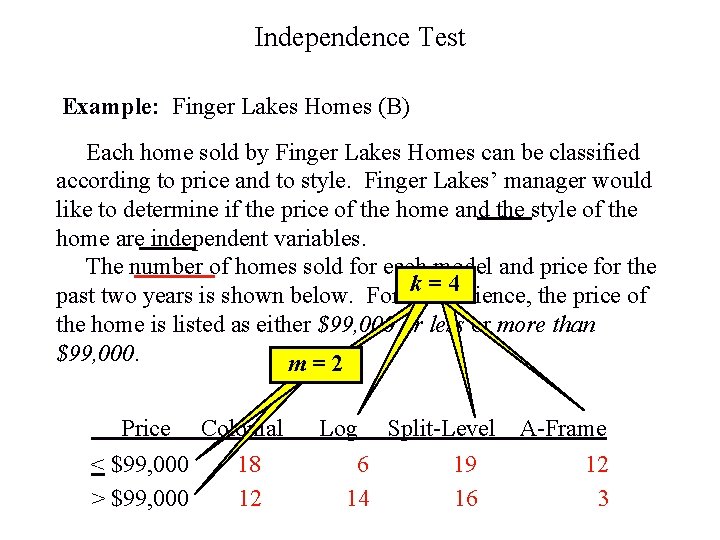
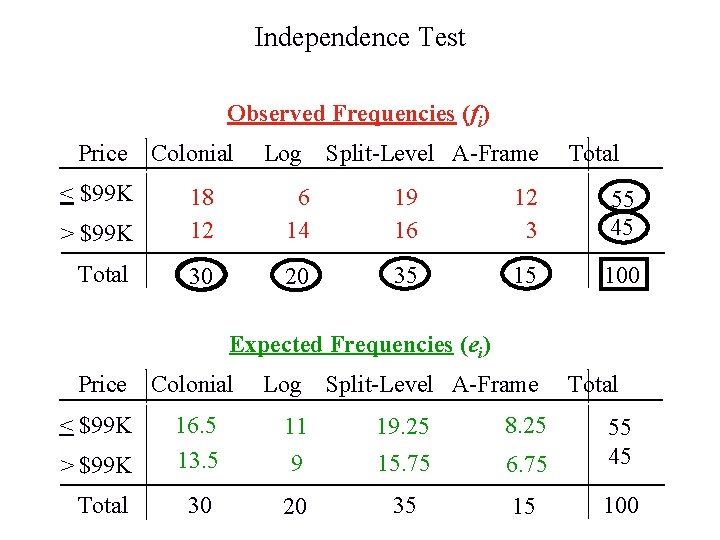
Independence Test Example: Finger Lakes Homes (B) Each home sold by Finger Lakes Homes can be classified according to price and to style. Finger Lakes’ manager would like to determine if the price of the home and the style of the home are independent variables. The number of homes sold for each model and price for the k=4 past two years is shown below. For convenience, the price of the home is listed as either $99, 000 or less or more than $99, 000. m=2 Price Colonial < $99, 000 18 > $99, 000 12 Log Split-Level 6 19 14 16 A-Frame 12 3

Independence Test Observed Frequencies (fi) Price < $99 K Colonial Log Split-Level A-Frame Total > $99 K 18 12 6 14 19 16 12 3 55 45 Total 30 20 35 15 100 Expected Frequencies (ei) Price Colonial Log Split-Level A-Frame Total < $99 K 11 19. 25 8. 25 > $99 K 16. 5 13. 5 9 15. 75 6. 75 55 45 Total 30 20 35 15 100

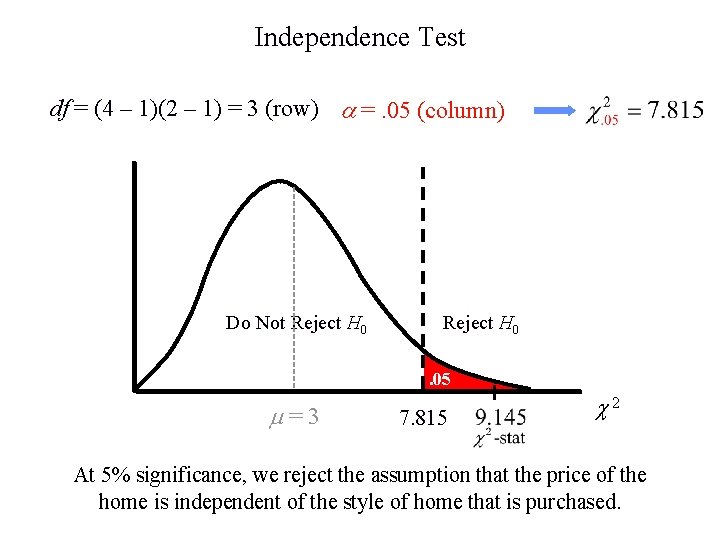
Independence Test Hypotheses H 0: Price of the home is independent of the style of the home that is purchased Ha: Price of the home is not independent of the style of the home that is purchased Compute test statistic

Independence Test df = (4 – 1)(2 – 1) = 3 (row) =. 05 (column) Do Not Reject H 0. 05 =3 7. 815 2 At 5% significance, we reject the assumption that the price of the home is independent of the style of home that is purchased.

Goodness of Fit Test: Poisson Distribution 1. Set up the null and alternative hypotheses. 2. Select a random sample and a. Record observed frequencies b. Estimate mean number of occurrences 3. Compute expected frequency of occurrences ei for each value of the Poisson random variable. 4. Compute the value of the test statistic. 5. Reject H 0 if df = k – p – 1

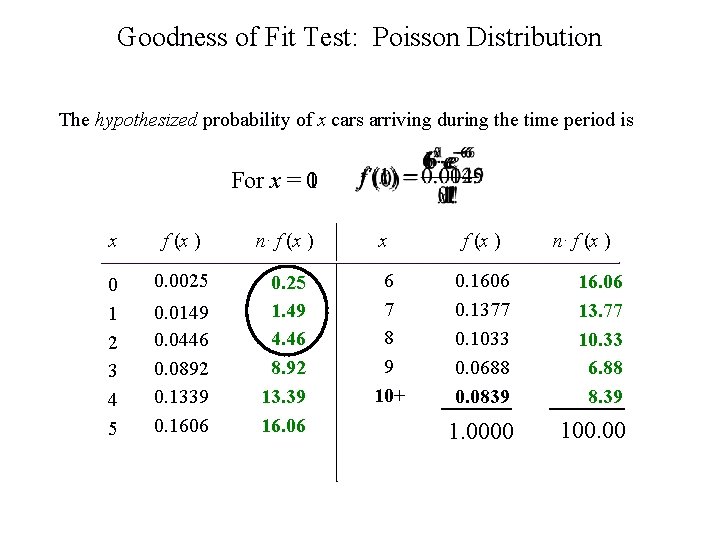
Goodness of Fit Test: Poisson Distribution Example: Troy Parking Garage In studying the need for an additional entrance to a city parking garage, a consultant has recommended an analysis approach that is applicable only in situations where the number of cars entering during a specified time period follows a Poisson distribution. A random sample of n = 100 one-minute time intervals resulted in the customer arrivals listed below. A statistical test must be conducted to see if the assumption of a Poisson distribution is reasonable. # of Arrivals 0 1 2 Frequency 1 4 10 14 20 12 12 9 0 3 4 5 6 7 8 otal Arrivals = 0(0) + 1(1) + 2(4) + 3(10) +. 9 10 11 12 8 6 3 1 . . + 12(1) = 600 Total one-minute intervals = n = 0 + 1 + 4 + 10 +. . . + 1 = 100 Estimate of = 600/100 = 6

Goodness of Fit Test: Poisson Distribution The hypothesized probability of x cars arriving during the time period is For x = 01 x f (x ) n∙ f (x ) x f (x ) 0 1 2 3 4 5 0. 0025 0. 25 1. 49 4. 46 8. 92 13. 39 16. 06 6 7 8 9 10+ 0. 1606 0. 1377 0. 1033 0. 0688 0. 0839 16. 06 13. 77 10. 33 6. 88 8. 39 1. 0000 100. 00 0. 0149 0. 0446 0. 0892 0. 1339 0. 1606 n∙ f (x )

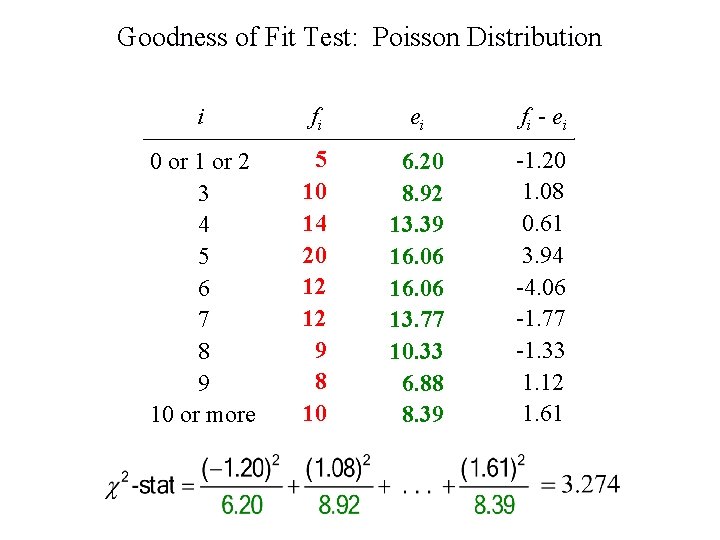
Goodness of Fit Test: Poisson Distribution i fi ei fi - ei 0 or 1 or 2 3 4 5 6 7 8 9 10 or more 5 10 14 20 12 12 9 8 10 6. 20 8. 92 13. 39 16. 06 13. 77 10. 33 6. 88 8. 39 -1. 20 1. 08 0. 61 3. 94 -4. 06 -1. 77 -1. 33 1. 12 1. 61

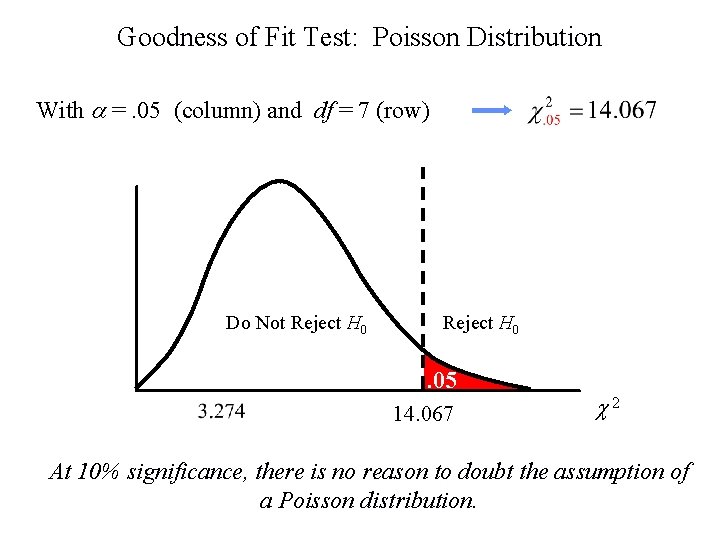
Goodness of Fit Test: Poisson Distribution With =. 05 (column) and df = 7 (row) Do Not Reject H 0 . 05 14. 067 2 At 10% significance, there is no reason to doubt the assumption of a Poisson distribution.

Goodness of Fit Test: Normal Distribution 1. State the null and alternative hypotheses. 2. Select a random sample and a. Compute the mean and standard deviation (p = 2). b. Define intervals so that ei > 5 is in the ith interval c. For each interval, record observed frequencies fi 3. Compute ei for each interval. 4. Compute the value of the test statistic. if ei > 5, this has a chi-square distribution 5. Reject H 0 if df = k – p – 1

Goodness of Fit Test: Normal Distribution Example: IQ Computers (one better than HP? ) manufactures and sells a general purpose microcomputer. As part of a study to evaluate sales personnel, management wants to determine, at a 5% significance level, if the annual sales volume (number of units sold by a salesperson) follows a normal probability distribution. A simple random sample of 33 of the salespeople was taken and their numbers of units sold are below. 33 64 83 43 65 84 44 66 85 45 68 86 52 70 91 52 72 92 56 73 94 58 63 63 64 73 74 74 75 98 101 102 105 n = 33, x = 71. 76, s = 18. 47

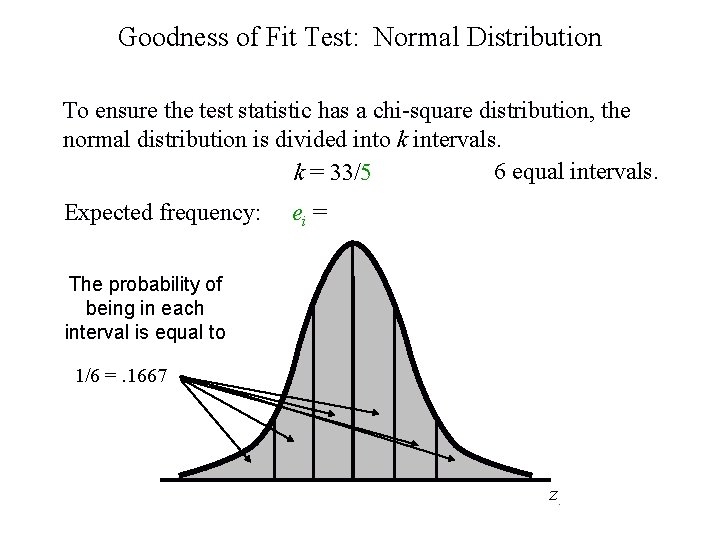
Goodness of Fit Test: Normal Distribution To ensure the test statistic has a chi-square distribution, the normal distribution is divided into k intervals. 6 equal intervals. k = 33/5 = 6. 6 Expected frequency: ei = 33/6 = 5. 5 The probability of being in each interval is equal to 1/6 =. 1667 z.

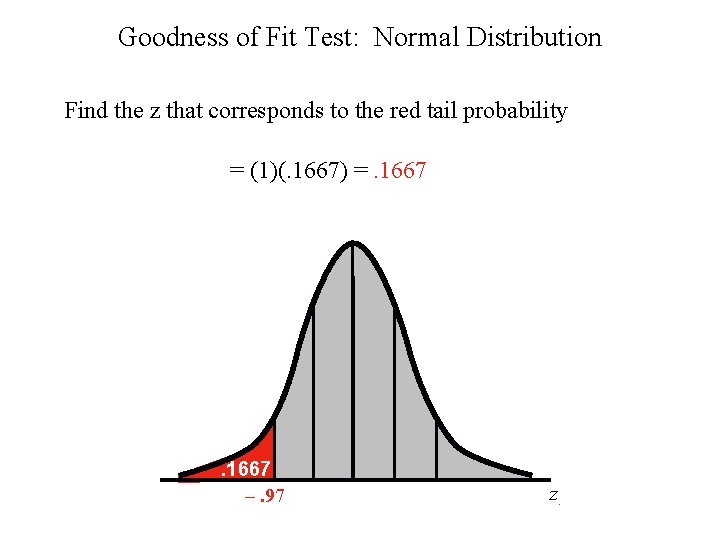
Goodness of Fit Test: Normal Distribution Find the z that corresponds to the red tail probability = (1)(. 1667) =. 1667 –. 97 z.

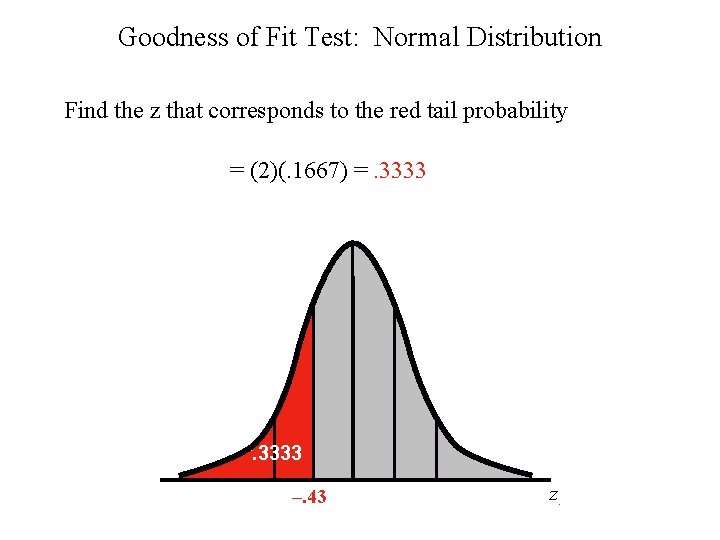
Goodness of Fit Test: Normal Distribution Find the z that corresponds to the red tail probability = (2)(. 1667) =. 3333 –. 43 z.

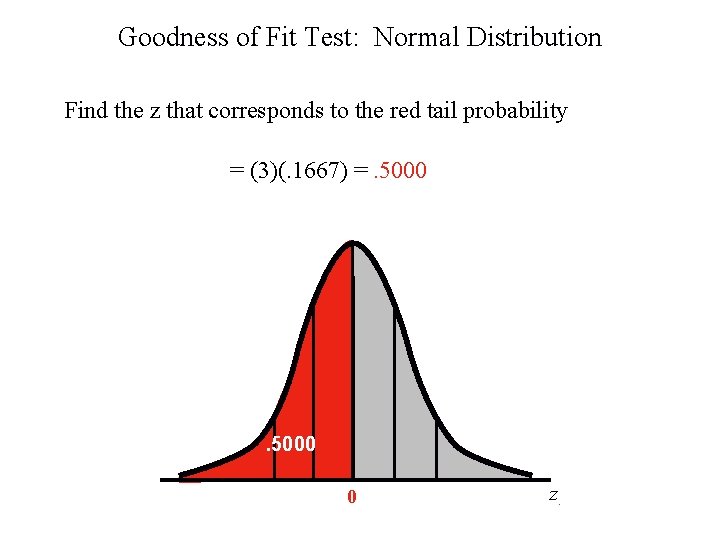
Goodness of Fit Test: Normal Distribution Find the z that corresponds to the red tail probability = (3)(. 1667) =. 5000 0 z.

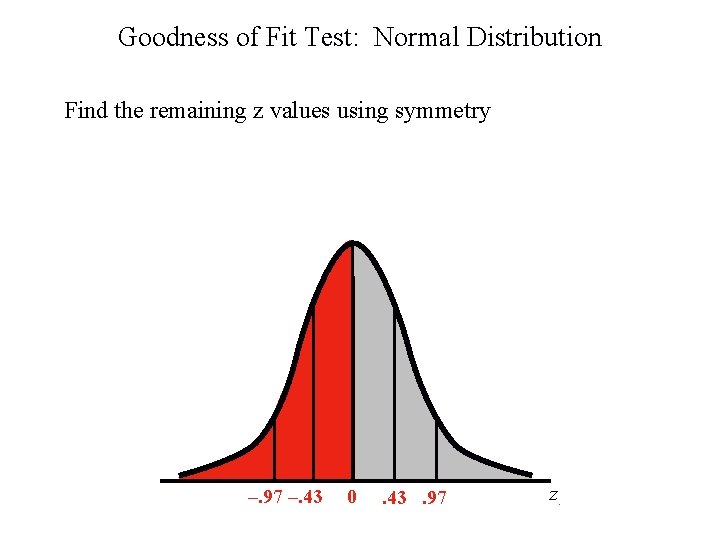
Goodness of Fit Test: Normal Distribution Find the remaining z values using symmetry –. 97 –. 43 0 . 43. 97 z.

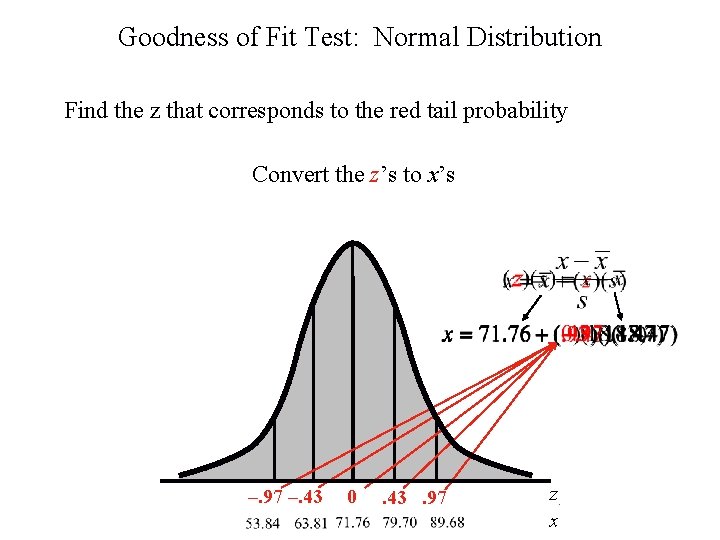
Goodness of Fit Test: Normal Distribution Find the z that corresponds to the red tail probability Convert the z’s to x’s –. 97 –. 43 0 . 43. 97 z. x

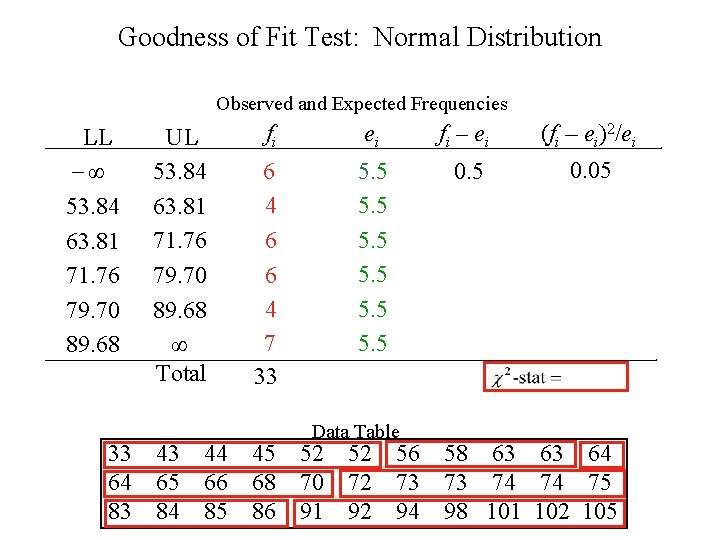
Goodness of Fit Test: Normal Distribution Observed and Expected Frequencies LL -∞ 53. 84 63. 81 71. 76 79. 70 89. 68 33 64 83 UL 53. 84 63. 81 71. 76 79. 70 89. 68 ∞ Total 43 65 84 44 66 85 fi ei fi – ei (fi – ei)2/ei 6 4 6 6 4 7 33 5. 5 5. 5 33 0. 5 -1. 5 0. 05 0. 41 1. 36 45 68 86 Data Table 52 70 91 52 72 92 56 73 94 58 63 63 64 73 74 74 75 98 101 102 105

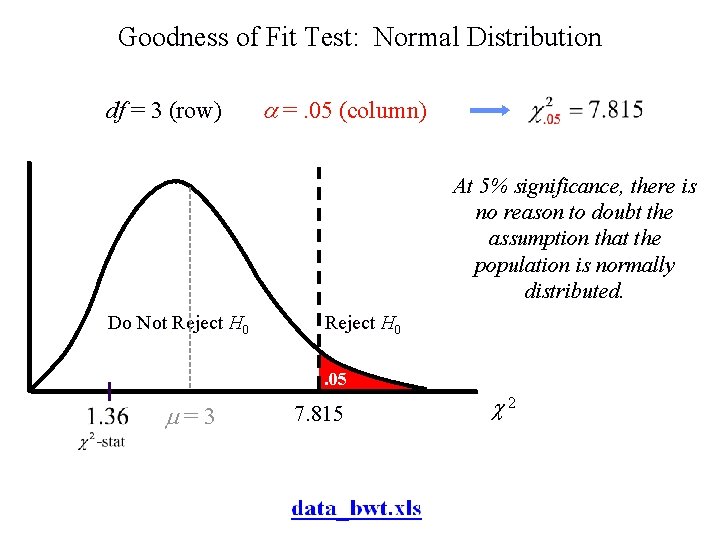
Goodness of Fit Test: Normal Distribution df = 3 (row) =. 05 (column) At 5% significance, there is no reason to doubt the assumption that the population is normally distributed. Do Not Reject H 0. 05 =3 7. 815 2