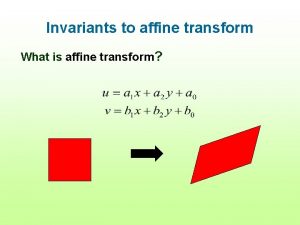
Geometria euclidea affine e proiettiva Anno accademico 200809

Geometria euclidea, affine e proiettiva Anno accademico 2008/09 Presentazione del corso g. e. a. p. 08/09 1

Quante geometrie? Felix Klein, 1872, “Programma di Erlangen” S, insieme di punti G, gruppo di trasformazioni di S una teoria geometrica di S consiste nello studio delle proprietà delle figure di S che sono invarianti rispetto alle trasformazioni del gruppo G g. e. a. p. 08/09 1

Figure equivalenti rispetto a G Dati • F, F’ sottoinsiemi di S, figure • φ Є G, φ: S → S bigettiva (trasformazione) diremo che • F è equivalente a F’ rispetto a G , F G F’ se F = φ(F’) Esercizio • La relazione G è riflessiva, simmetrica, transitiva g. e. a. p. 08/09 1

Dal programma di Klein segue: se la geometria dello spazio S dotato del gruppo G è la ricerca e lo studio delle proprietà delle figure di S che sono invarianti rispetto alle trasformazioni del gruppo G, allora figure equivalenti rispetto a G hanno le stesse proprietà geometriche. g. e. a. p. 08/09 1

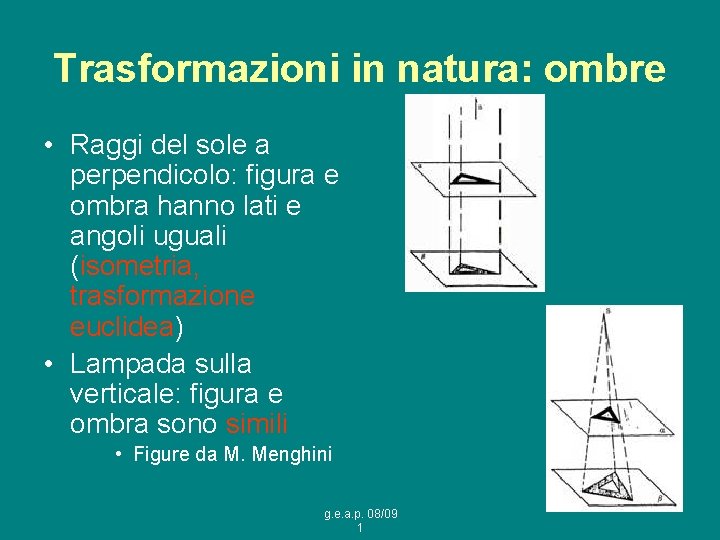
Trasformazioni in natura: ombre • Raggi del sole a perpendicolo: figura e ombra hanno lati e angoli uguali (isometria, trasformazione euclidea) • Lampada sulla verticale: figura e ombra sono simili • Figure da M. Menghini g. e. a. p. 08/09 1

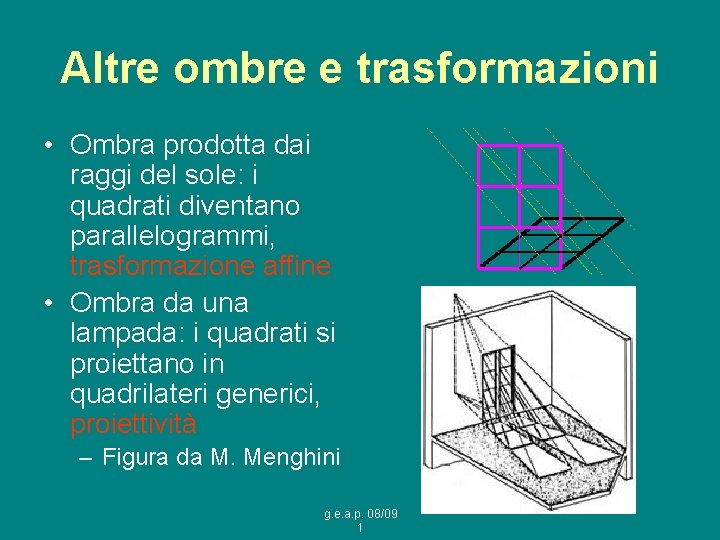
Altre ombre e trasformazioni • Ombra prodotta dai raggi del sole: i quadrati diventano parallelogrammi, trasformazione affine • Ombra da una lampada: i quadrati si proiettano in quadrilateri generici, proiettività – Figura da M. Menghini g. e. a. p. 08/09 1

Perché la geometria proiettiva? E’ il modello matematico che spiega l’insieme delle tecniche – la prospettiva trovate dai pittori del Rinascimento – Leon Battista Alberti, De pictura, 1435 – Piero della Francesca, De prospectiva pingendi, 1482 – Albrecht Dürer, L’arte della misura, 1525 g. e. a. p. 08/09 1

Pittura e geometria poiché la geometria è il giusto fondamento di ogni pittura, ho deciso di insegnare i suoi rudimenti e principi a tutti i giovani che vogliono apprendere l’arte. . . (A. Dürer) • Dürer è in Italia, dove, a Venezia nel 1505 viene stampata Ottica, di Euclide • Gli studi sulla prospettiva trovano compimento nell’opera di Desargues, La prospettiva, 1636 – http: //www-groups. dcs. stand. ac. uk/~history/Hist. Topics/Art. html g. e. a. p. 08/09 1

Che cosa è la prospettiva? • Per farcene un’idea, cominciamo osservando alcuni quadri • Molte fra le immagini che seguono sono tratte dal CD allegato al testo “Le geometrie della visione” di Catastini. Ghione • Per i disegni, è stato usato un software di geometria g. e. a. p. 08/09 1

Confrontate questo dipinto… Duccio da Boninsegna (ca. 1255 -1319) Nozze di Canaan g. e. a. p. 08/09 1

…con questo dipinto Raffaello Sanzio (1483 -1520) Sposalizio della vergine g. e. a. p. 08/09 1

g. e. a. p. 08/09 1

g. e. a. p. 08/09 1

Il modello della piramide visiva (figura da E. Danti, 1536 -1586) g. e. a. p. 08/09 1

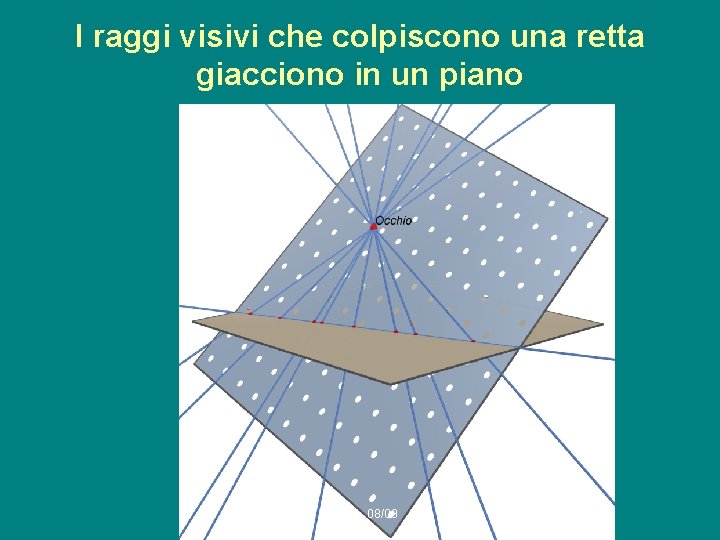
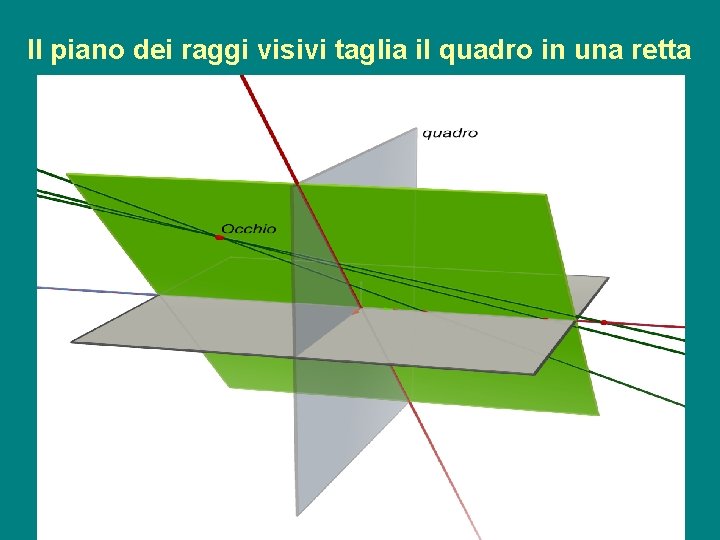
I raggi visivi che colpiscono una retta giacciono in un piano g. e. a. p. 08/09 1

Il piano dei raggi visivi taglia il quadro in una retta g. e. a. p. 08/09 1

Corrispondenza tra retta osservata e retta immagine • Supponiamo che l’occhio segua un punto P che si muove lungo una retta… • C: Documents and Settingsdaprile 1Documentigeap 0809rett aguardata. fig • La corrispondenza P P’ è una bigezione tra le due rette? g. e. a. p. 08/09 1

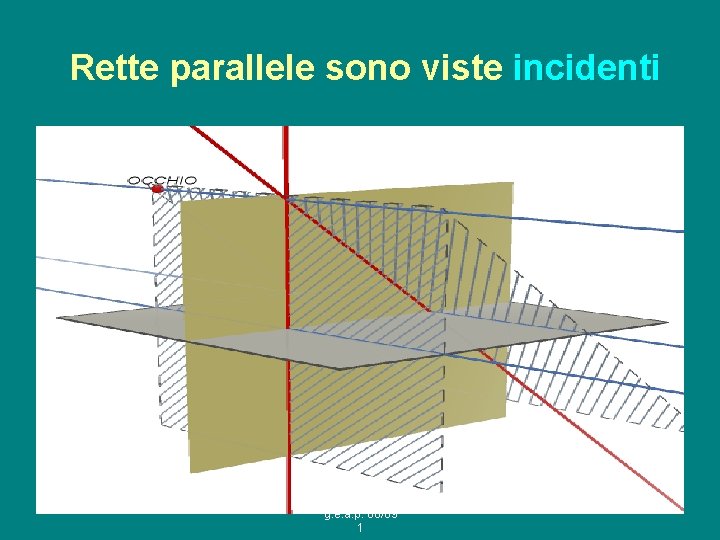
Ci sono delle eccezioni • C’è un punto I sulla retta guardata che non ha corrispondente sul quadro e c’è un punto J sul quadro che non è immagine di nessun punto sulla retta osservata. • Le eccezioni sono dovute all’esistenza di rette parallele. • Come vengono viste nel quadro due rette parallele del pavimento? g. e. a. p. 08/09 1

Rette parallele sono viste incidenti g. e. a. p. 08/09 1

Il punto di fuga g. e. a. p. 08/09 1

Punti all’infinito • Le immagini di due rette parallele si intersecano in un punto, il punto di fuga • che si può pensare come immagine di un punto lontano, dove convergono le due rette parallele, il punto all’infinito delle due rette • La proiezione dall’occhio, corrispondenza quasi biunivoca tra una retta e la sua immagine, diviene bijettiva con l’introduzione dei punti all’infinito g. e. a. p. 08/09 1

In linguaggio simbolico Siano: • r la retta osservata dall’occhio O • r’ la retta sezione del piano del quadro con il piano di O ed r • nel fascio di centro O, p la retta parallela ad r, p’ la parallela ad r’ • I = r p’, J =r’ p • R il punto all’infinito di r • R’ il punto all’infinito di r’. g. e. a. p. 08/09 1

Proiezione di centro O È l’applicazione O: r r’, definita come segue • se P r, P I, P R , O(P) = P’ , tale che O, P, P’ siano allineati • se P = I, O(P) = R’ • se P = R , O(P)= J O è una bijezione g. e. a. p. 08/09 1

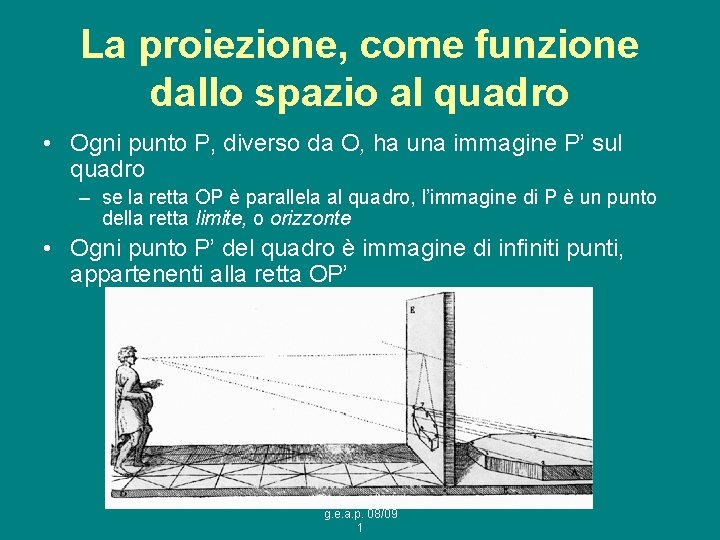
La proiezione, come funzione dallo spazio al quadro • Ogni punto P, diverso da O, ha una immagine P’ sul quadro – se la retta OP è parallela al quadro, l’immagine di P è un punto della retta limite, o orizzonte • Ogni punto P’ del quadro è immagine di infiniti punti, appartenenti alla retta OP’ g. e. a. p. 08/09 1

Da un’applicazione non iniettiva… Siano: S lo spazio, il piano del quadro, un piano che non passi per O. L’applicazione non iniettiva “proiezione da O” O: S induce un’applicazione O| : , che è iniettiva se ai due piani si aggiungono i punti impropri g. e. a. p. 08/09 1

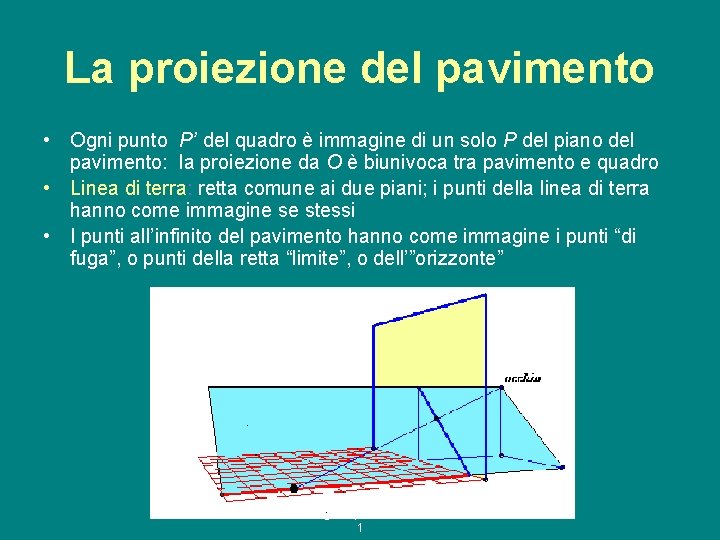
La proiezione del pavimento • Ogni punto P’ del quadro è immagine di un solo P del piano del pavimento: la proiezione da O è biunivoca tra pavimento e quadro • Linea di terra: retta comune ai due piani; i punti della linea di terra hanno come immagine se stessi • I punti all’infinito del pavimento hanno come immagine i punti “di fuga”, o punti della retta “limite”, o dell’”orizzonte” g. e. a. p. 08/09 1

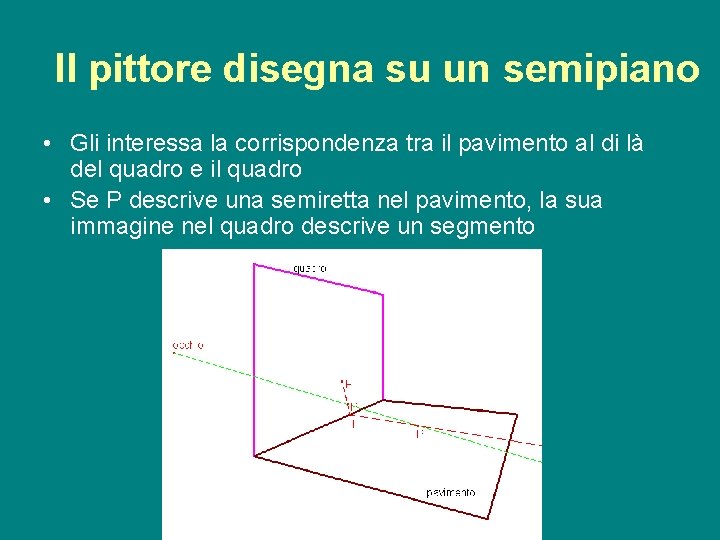
Il pittore disegna su un semipiano • Gli interessa la corrispondenza tra il pavimento al di là del quadro e il quadro • Se P descrive una semiretta nel pavimento, la sua immagine nel quadro descrive un segmento g. e. a. p. 08/09 1

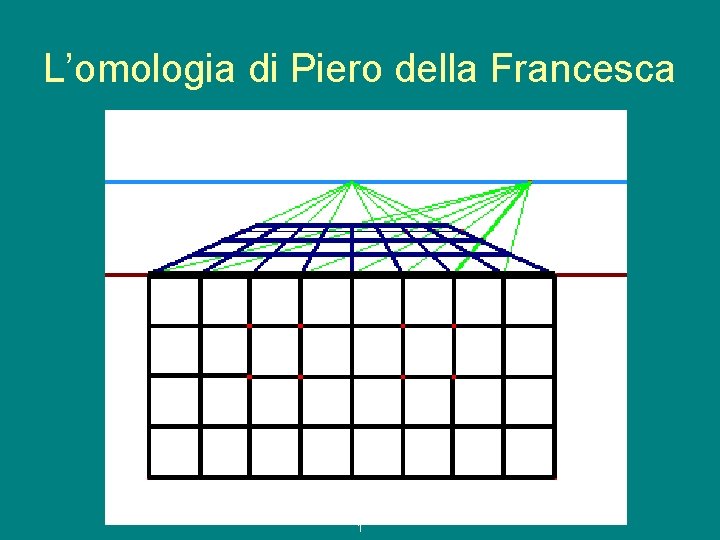
Iniziare dal pavimento • La raffigurazione del pavimento è un espediente per dare la sensazione di profondità • Alle tecniche empiriche usate nelle botteghe del suo tempo, Piero della Francesca sostituisce una tecnica basata sullo studio di una trasformazione della geometria proiettiva, detta “omologia” g. e. a. p. 08/09 1

L’omologia di Piero della Francesca g. e. a. p. 08/09 1

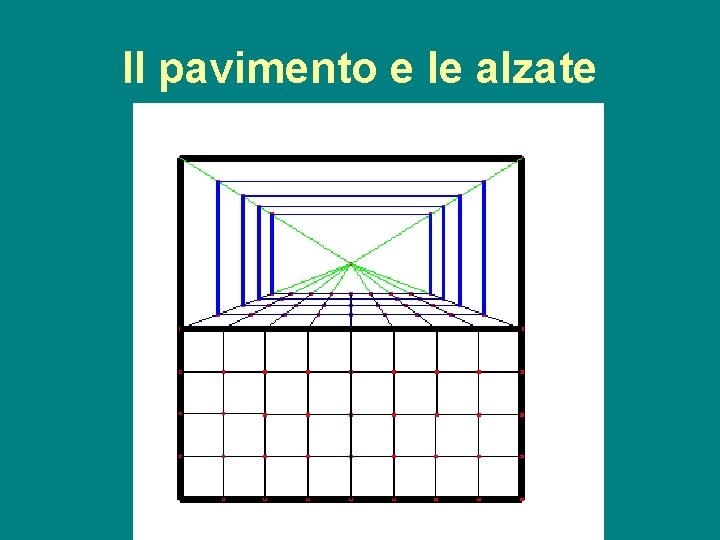
Il pavimento e le alzate g. e. a. p. 08/09 1

Il pavimento a piastrelle di Fra Lippi g. e. a. p. 08/09 1

La città ideale (scuola di Piero della Francesca o L. B. Alberti ? ) g. e. a. p. 08/09 1

Scopo del corso • Conoscere i fondamenti della geometria proiettiva • Classificare le trasformazioni del piano proiettivo in sé, riconoscendo tra queste l’omologia di Piero • Studiare le geometrie affine ed euclidea come sottogeometrie della geometria proiettiva • Costruire le classificazioni proiettiva, affine, metrica delle curve piane del secondo ordine (coniche) g. e. a. p. 08/09 1

Indice indicativo • Il piano proiettivo come ampliamento del piano della geometria elementare • Costruzioni grafiche: birapporto, prospettività, proiettività tra rette • Spazi proiettivi, dualità • Proiettività del piano, omologia • Affinità, isometrie • Polarità, coniche e quadriche – Classificazioni proiettive e affini g. e. a. p. 08/09 1

Prequisiti al corso • Geometria analitica elementare: – equazioni cartesiane e parametriche di rette e coniche nel piano, – di rette, piani, cilindri, sfere nello spazio. • Sistemi lineari: – il teorema di Rouché-Capelli, autosoluzioni di un sistema lineare omogeneo. • Algebra lineare: – spazi vettoriali, sottospazi, dimensioni, formula di Grassmann, – applicazioni lineari e matrici associate, nucleo e immagine di un’applicazione lineare, relazione tra rango della matrice e dimensioni del nucleo e dell’immagine dell’applicazione associata alla matrice; – autovalori e autovettori g. e. a. p. 08/09 1

Testi • Beltrametti, Carletti, Gallarati, Monti Bragadin, Lezioni di geometria analitica e proiettiva, Bollati Boringhieri, Torino, 2002 • Catastini-Ghione, Le geometrie della visione, Springer, 2003, http: //www. mat. uniroma 2. it/mep • Sernesi, Geometria 1, Bollati Boringhieri, Torino, 1989 • Stillwell, The four pillars of geometry, Springer, New York, 2005 g. e. a. p. 08/09 1

Siti utili • Siti di storia: – http: //www-groups. dcs. stand. ac. uk/~history/Hist. Topics/Art. html – http: //www-history. mcs. standrews. ac. uk/Hist. Topics/Architecture. html • Altri siti di geometria – www. treccani. it/site/Scuola/Zoom/prospettiva/scuola_zo om. htm • Appunti ed esercizi del corso e altri materiali http: //www. mat. unical. it/%7 Edaprile/Materiali. htm g. e. a. p. 08/09 1

Aiuti allo studio • Un compito a casa ogni settimana (per sette volte, possibilmente) • esercitazione scritta a metà corso influiscono sul voto finale Proposta, basata sull’esperienza dell’anno scorso: indicato con v il voto della prova intermedia, • Se v < 18 , non ha nessun effetto sul voto finale • Se 18 v 26 , viene aggiunto 1 punto al voto finale • Se 27 v 30 con lode , vengono aggiunti 2 punti al voto finale. • A chi consegna almeno la metà dei compiti , viene aggiunto un punto • Se invece almeno quattro compiti a casa erano corretti, due punti g. e. a. p. 08/09 1

Aiuti allo studio Ricevimento lunedì dalle 14. 30 alle 16, sesto piano (livello ponte carrabile) per appuntamento: tel. 0984/496452, posta el. m. daprile@unical. it • • Esame scritto e orale sugli argomenti svolti nelle lezioni. E’ obbligatoria la prenotazione https: //didattica. unical. it/ Tutor? g. e. a. p. 08/09 1