Gears Introduction A gear is a wheel with























- Slides: 34

Gears

Introduction • A gear is a wheel with teeth on its outer edge. • Gears rotate on a central axis. • The teeth of one gear mesh with or engage the teeth of another gear - transmitting rotary motion. • Gears are used to change the torque, speed, and direction of rotation.

Driver and Driven Direction of Rotation • Two meshed gears always rotate in opposite directions. • The driver (or input) gear would be the gear that is moved by a crank handle or motor. • The driver’s teeth engage the teeth of the driven (or output) gear, causing it to rotate.

Gear Ratio • A gear ratio is the ratio used to determine the angular speed and torque of a geared system. Number of driven teeth : Number of driver teeth Also written as: Driven teeth Driver teeth • If a set of gears has a driver and driven gearof the same size. The gear ratio would be 1: 1. • This causes a change in the direction of the motion with no change to speed or torque.

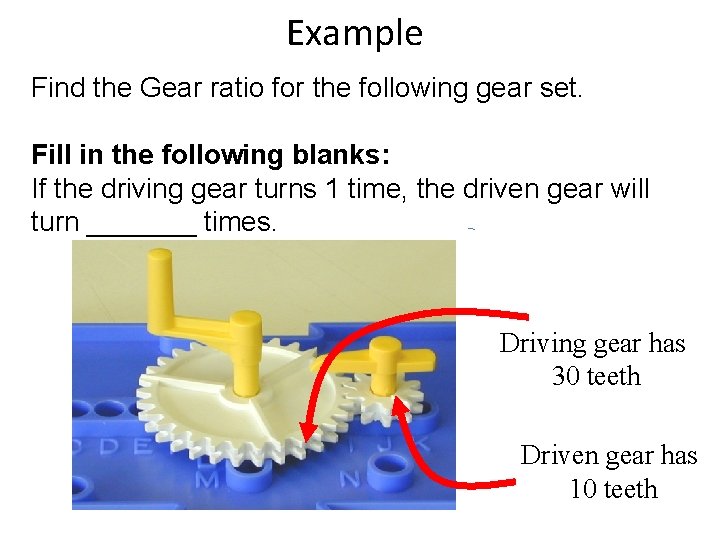
Example Find the Gear ratio for the following gear set. Fill in the following blanks: If the driving gear turns 1 time, the driven gear will turn _______ times. Driving gear has 30 teeth Driven gear has 10 teeth

Gear Ratio Practice Find the Gear Ratios for these examples: 1. A 5 -tooth gear driving a 45 -tooth gear. 9/1 or 9: 1 2. A 3 -tooth gear driving a 12 -tooth gear. 4/1 or 4: 1 3. A 12 -tooth gear driving a 3 -tooth gear. 1/4 or 1: 4

Gearing Up: Need for Speed • To increase the speed the driver should be larger than the driven gear. • Example: The driver gear has 60 teeth and the driven gear is 30 teeth. • Gear ratio = 30/60 = ½ or 1: 2 • This means that for every 1 turn of the driver gear, the driven will rotate 2 times.

Gearing Up: Need for Speed • With this 1: 2 ratio, the speed of the driven gear is 2 times greater than the input. Why Gear Up? • Using the top gear on your bike, you can make the back wheel spin faster than you can pedal. • A fan’s blades can whir at a greater speed than the electric motor that drives it.

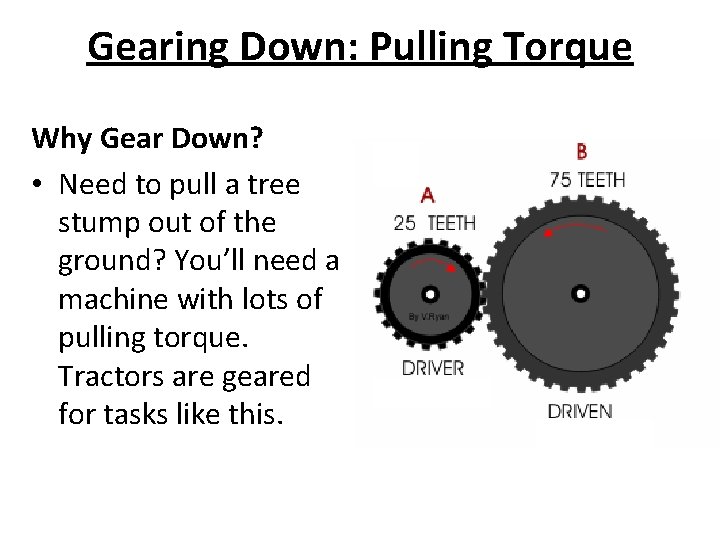
Gearing Down: Pulling Torque • To increase the torque the driver should be smaller than the driven. • The force translated from the driver gear to the driven gear is the same. • However, the driven gear has a longer lever arm, therefore the torque is larger for the driven gear. • Example: The driven torque is multiplied by the gear ratio which is 3/1. Therefore, the torque of the driven gear is 3 times greater than the torque of the driver gear. Gear ratio = 75/25 = 3/1

Gearing Down: Pulling Torque Why Gear Down? • Need to pull a tree stump out of the ground? You’ll need a machine with lots of pulling torque. Tractors are geared for tasks like this.

Speed and Torque • Torque and speed are inversely proportional. • 1 A. This gearing increases the speed but decreases the torque. • 1 B. This gearing increases the torque, but decreases the speed.

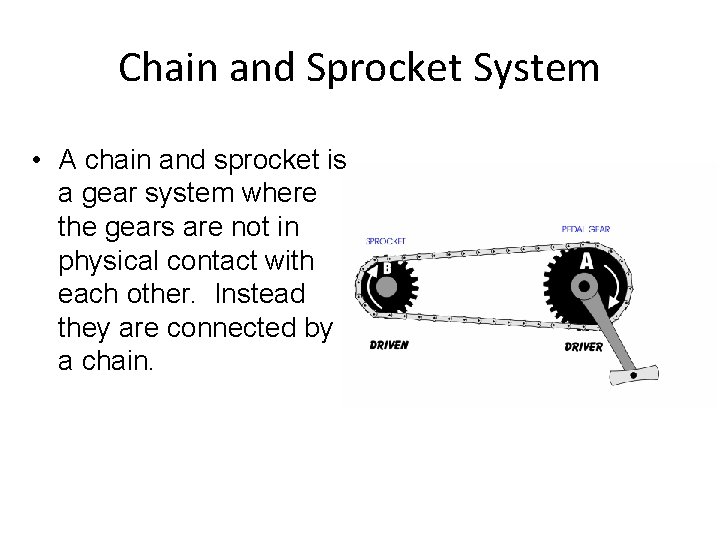
Chain and Sprocket System • A chain and sprocket is a gear system where the gears are not in physical contact with each other. Instead they are connected by a chain.

• The same principle of gear ratio applies to chain and sprocket systems.

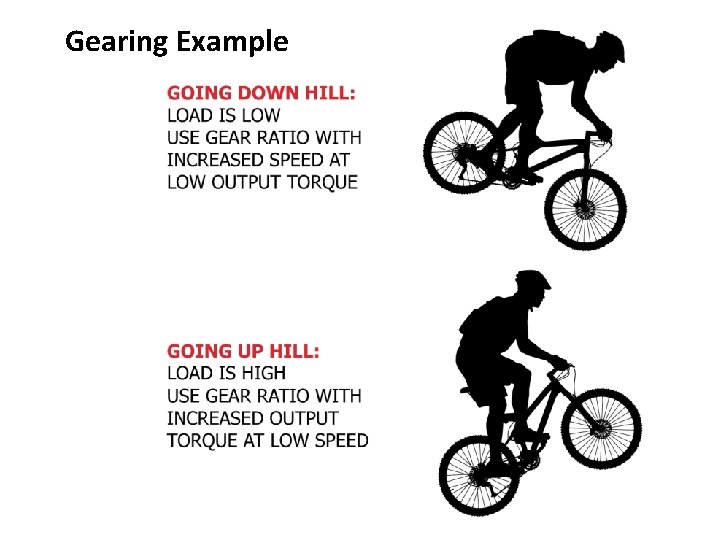
Gearing Example

Review You can calculate Gear Ratio by dividing the number of teeth on the Driven Gear by the number of teeth on the Driving Gear Ratio = # teeth on Driven Gear # teeth on Driving Gear

Gears Are Like People Little Ones Have To Move Faster To Keep Up with The Big Ones

Possible VEX gear ratios

Gear Trains • Sometimes the driver and follower must rotate the same direction. • Inserting an idler gear between the driver and follower is the simplest way to achieve this.

Gear Ratio of Gear Trains • In gear trains the ratio will change from set to set. Multiplying the gear ratio for each set of gears will give you the net gear ratio for the train. • In a gear train with each gear on a separate axle the idler gears can be ignored. Therefore the net gear ratio can still be found by: Driven teeth Driver teeth

Example: • The driving gear has 30 teeth, the idler gear has 90 teeth and the driven gear has 15 teeth. – The ratio for A: B is 3/1; the ratio for B: C is 1/6. Net gear ratio = 3/1 x 1/6 = 1/2. – Ignoring the idler gears results in the same gear ratio. A: C = 15/30 = 1/2

Gear Ratio of Gear Trains • In a gear train in which some gears share the same axle the gear ratio must be found by multiplying each individual gear ratio.

Example: • Find the ratios for each set of gears. – A: B is 40/120 = 1/3 – C: D is 20/80 = 1/4 – The net gear ratio = 1/3 x 1/4 = 1/12.

Gear Ratios and Calculating Speed

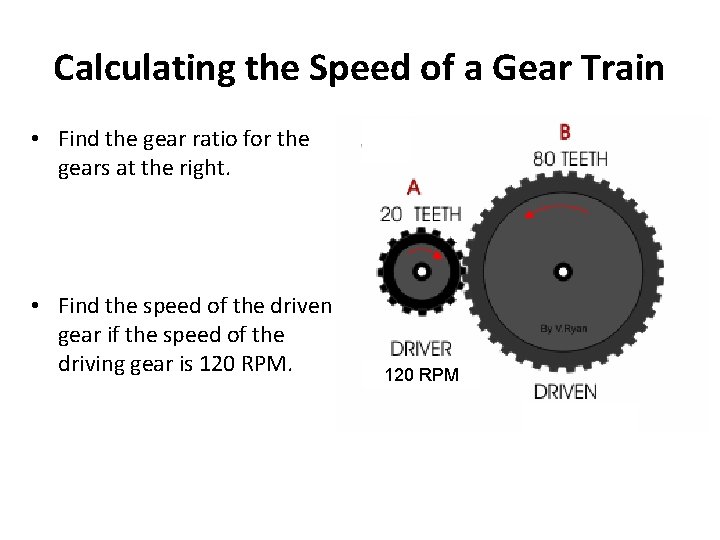
Calculating the Speed of a Gear Train • Use the gear ratio to determine the speed of the driven gear. • Rotational speed is given in revolutions per minute (RPM). • In the example to the right the gear ratio is ½ or 1: 2. 60 RPM

Calculating the Speed of a Gear Train • A 1: 2 gear ratio means that every 1 turn of the driver gear causes the driven gear to rotate 2 times. • If the driver turns at 60 RPM then the driven gear must turn at 2 x 60 RPM = 120 RPM • Large gears driving small gears speed them up. 60 RPM

Calculating the Speed of a Gear Train • In this example the gear ratio is 3: 1 or 3/1 which means for every 3 turns of the driver gear the driven gear turns 1 time. • If the driver turns at 60 RPM then the driven gear must turn at 60 RPM / 3 = 20 RPM • Small gears driving large gears slow them down. 60 RPM

Calculating the Speed of a Gear Train • Find the gear ratio for the gears at the right. • Find the speed of the driven gear if the speed of the driving gear is 120 RPM

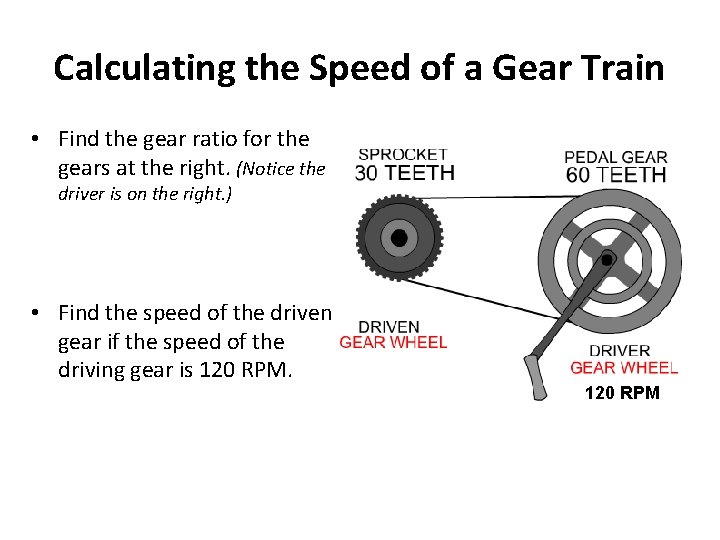
Calculating the Speed of a Gear Train • Find the gear ratio for the gears at the right. (Notice the driver is on the right. ) • Find the speed of the driven gear if the speed of the driving gear is 120 RPM

Gear Ratios and Calculating Torque

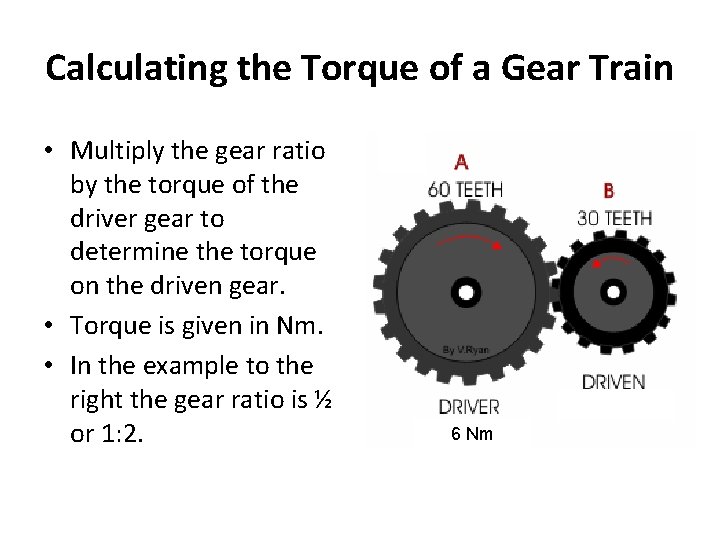
Calculating the Torque of a Gear Train • Multiply the gear ratio by the torque of the driver gear to determine the torque on the driven gear. • Torque is given in Nm. • In the example to the right the gear ratio is ½ or 1: 2. 6 Nm

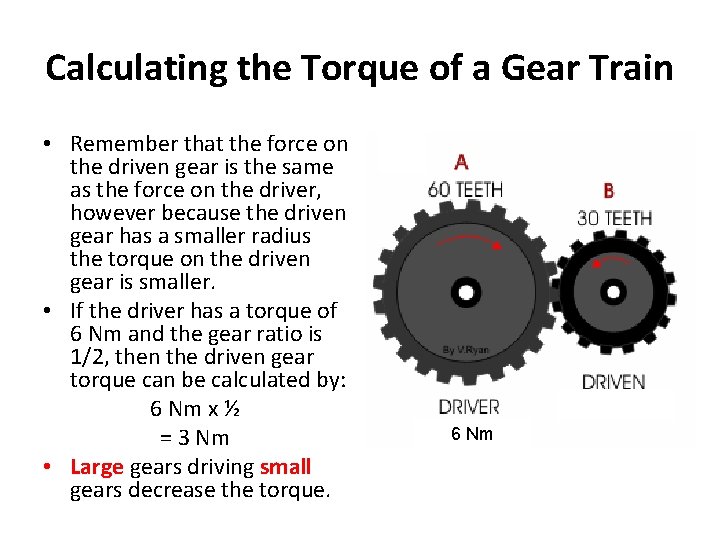
Calculating the Torque of a Gear Train • Remember that the force on the driven gear is the same as the force on the driver, however because the driven gear has a smaller radius the torque on the driven gear is smaller. • If the driver has a torque of 6 Nm and the gear ratio is 1/2, then the driven gear torque can be calculated by: 6 Nm x ½ = 3 Nm • Large gears driving small gears decrease the torque. 6 Nm

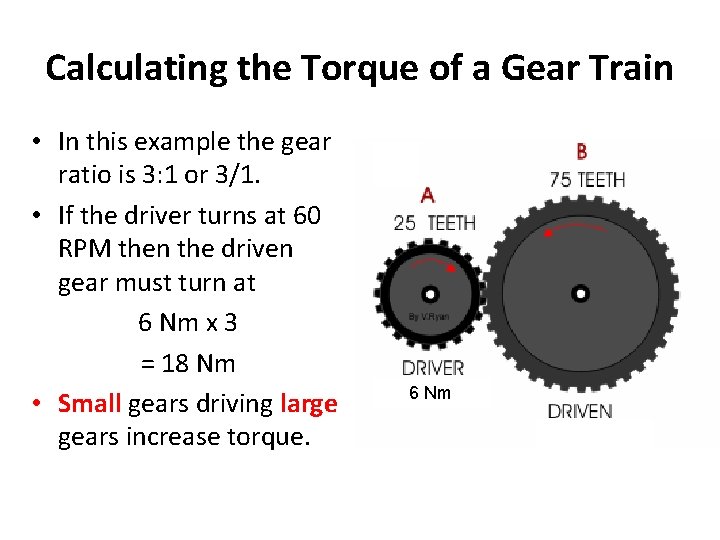
Calculating the Torque of a Gear Train • In this example the gear ratio is 3: 1 or 3/1. • If the driver turns at 60 RPM then the driven gear must turn at 6 Nm x 3 = 18 Nm • Small gears driving large gears increase torque. 6 Nm

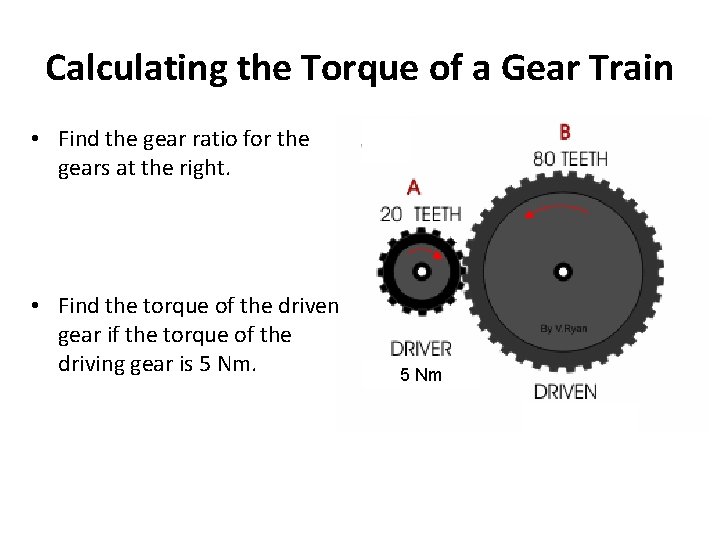
Calculating the Torque of a Gear Train • Find the gear ratio for the gears at the right. • Find the torque of the driven gear if the torque of the driving gear is 5 Nm

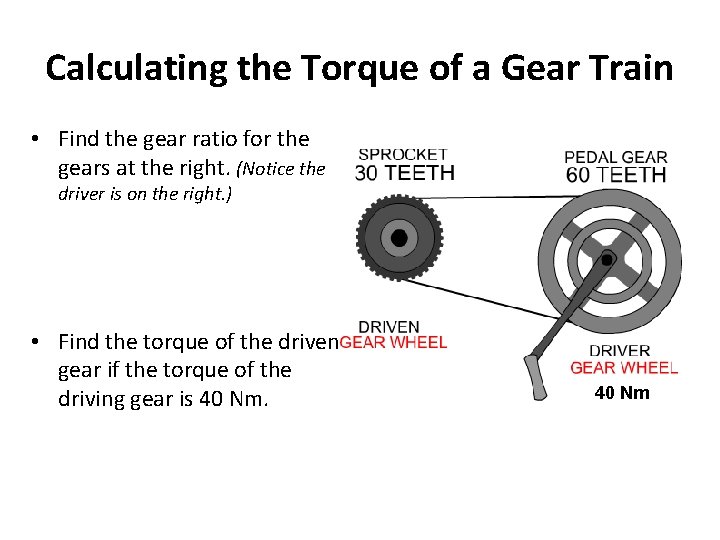
Calculating the Torque of a Gear Train • Find the gear ratio for the gears at the right. (Notice the driver is on the right. ) • Find the torque of the driven gear if the torque of the driving gear is 40 Nm
 Clean spreaders and check wheel-driven gears
Clean spreaders and check wheel-driven gears Wheel and axle lever
Wheel and axle lever Driver and driven gear
Driver and driven gear External gear pump vs internal gear pump
External gear pump vs internal gear pump The curves that satisfy fundamental law of gearing are,
The curves that satisfy fundamental law of gearing are, Chapter 74 ase questions
Chapter 74 ase questions Tire wheel and wheel bearing fundamentals
Tire wheel and wheel bearing fundamentals A slender tool attached to the needle clamp
A slender tool attached to the needle clamp Gear simple machine
Gear simple machine Evolution of fishing gears
Evolution of fishing gears Vex gear ratio
Vex gear ratio Compound machine with 3 simple machines
Compound machine with 3 simple machines Wounding gear
Wounding gear A bicycle chain fits tightly
A bicycle chain fits tightly Are gears wheels
Are gears wheels Which shaft turns fastest
Which shaft turns fastest Falling gears
Falling gears Charlie chaplin gears
Charlie chaplin gears Gears pulleys and levers
Gears pulleys and levers Ima of gears
Ima of gears Plain milling can be otherwise called as
Plain milling can be otherwise called as Gears sprockets pulleys
Gears sprockets pulleys Cpp depend
Cpp depend When equal bevel gears connect two shafts
When equal bevel gears connect two shafts Law of gearing
Law of gearing How many type of gear
How many type of gear Vex iq gear ratio simulator
Vex iq gear ratio simulator Types of gears
Types of gears Mahindra cie automotive ltd gear division
Mahindra cie automotive ltd gear division Spur gear force analysis
Spur gear force analysis Vex simple gear train with idler
Vex simple gear train with idler Bevel gear steering mechanism
Bevel gear steering mechanism Trident switchgear
Trident switchgear Screw pump vs gear pump
Screw pump vs gear pump Open gear grease spray
Open gear grease spray