From instantons to spontaneous fission rates P Jachimowicz

![Γ= A(T) exp[-S(T)] S S(T)= S(T) – action; x(tau) - a motion in the Γ= A(T) exp[-S(T)] S S(T)= S(T) – action; x(tau) - a motion in the](https://slidetodoc.com/presentation_image_h2/f79ecb0894bbfe4f1509aa7c233e81b4/image-2.jpg)


![G. S. configuration: P: 11/2+ [6 1 5] N: 13/2 - [7 1 6] G. S. configuration: P: 11/2+ [6 1 5] N: 13/2 - [7 1 6]](https://slidetodoc.com/presentation_image_h2/f79ecb0894bbfe4f1509aa7c233e81b4/image-7.jpg)









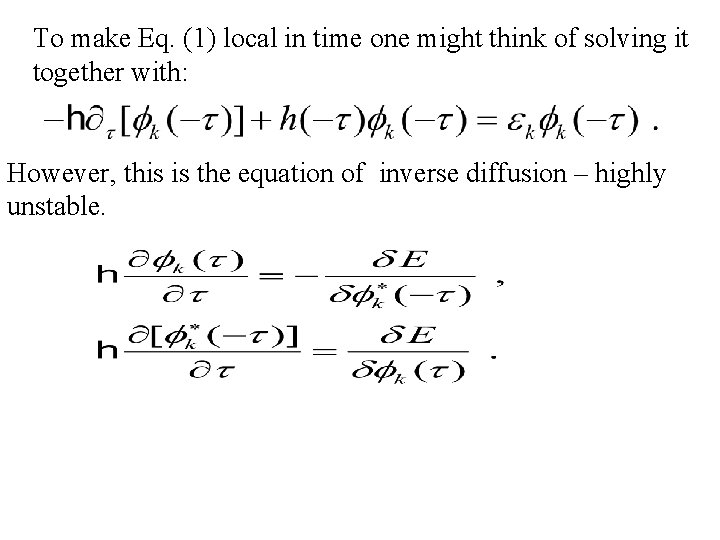










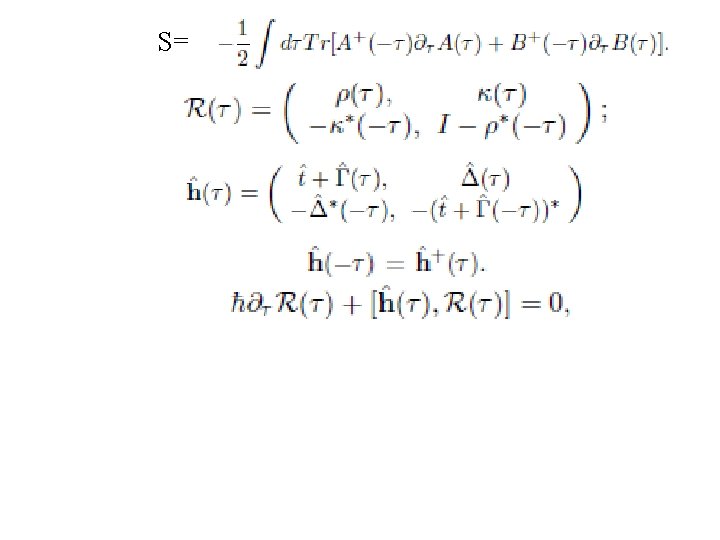



- Slides: 38

From instantons to spontaneous fission rates P. Jachimowicz (UZ) W. Brodziński, M. Kowal, J. Skalski (NCBJ) - Special interest: treating fission of odd & odd-odd nuclei and high-K isomers. - A difficulty in calculating action for odd-A nuclei or isomers – a breakdown of the adiabatic approximation. - Instanton-motivated selfconsistent (or non-selfconsistent) approach a) nonselfconsistent potential - h. o. model b) simple selfconsistent h. o. model c) non-selfconsistent model with pairing – varying delta
![Γ AT expST S ST ST action xtau a motion in the Γ= A(T) exp[-S(T)] S S(T)= S(T) – action; x(tau) - a motion in the](https://slidetodoc.com/presentation_image_h2/f79ecb0894bbfe4f1509aa7c233e81b4/image-2.jpg)
Γ= A(T) exp[-S(T)] S S(T)= S(T) – action; x(tau) - a motion in the imaginary time – with a negative kinetic energy or in the inverted potential. For a nucleus, enters the position-dependent mass. figures from E. Chudnovsky and J. Tejada, ” Macroscopic Quant. Tunneling of the Magnetic Moment”


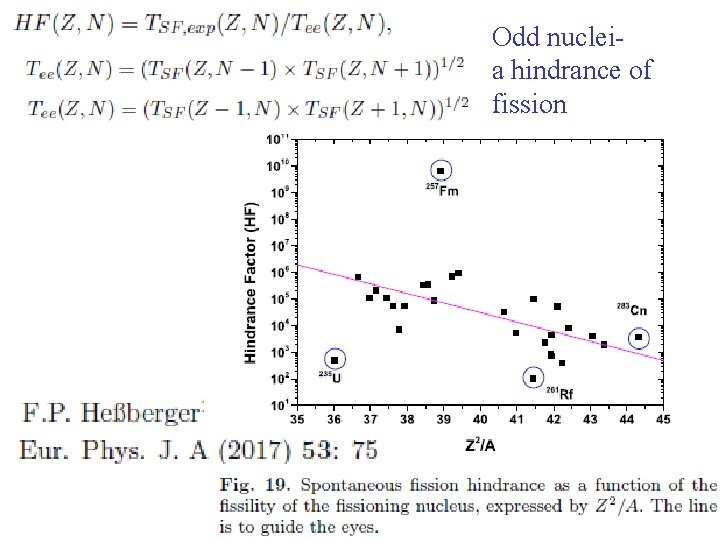
Odd nucleia hindrance of fission

Invoked reasons for Tsf increase: -for odd-Z or odd-N (vs. even), a smaller pairing gap causes an increase in the fission barrier and in the mass parameter (as given by a cranking expression); - blocking a specific configuration additionally rises the barrier (provided it is conserved in fission) – specialization. In calculations: the effect of keeping high-K number may be huge; if one does not suppress it, it seems the resulting half-lives in odd-A nuclei must come out too large.

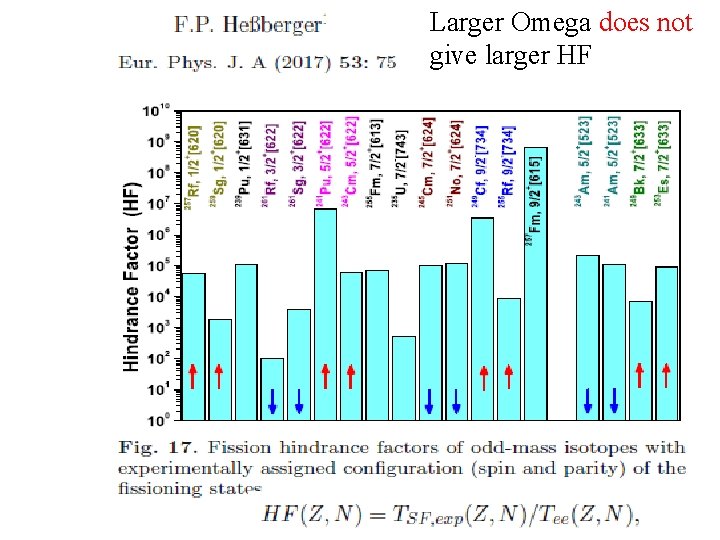
Larger Omega does not give larger HF
![G S configuration P 112 6 1 5 N 132 7 1 6 G. S. configuration: P: 11/2+ [6 1 5] N: 13/2 - [7 1 6]](https://slidetodoc.com/presentation_image_h2/f79ecb0894bbfe4f1509aa7c233e81b4/image-7.jpg)
G. S. configuration: P: 11/2+ [6 1 5] N: 13/2 - [7 1 6] Fixing the g. s. configuration rises the barrier by 6 Me. V. Even if configuration is not completely conserved, a substantial increase in fission half-life is expected.

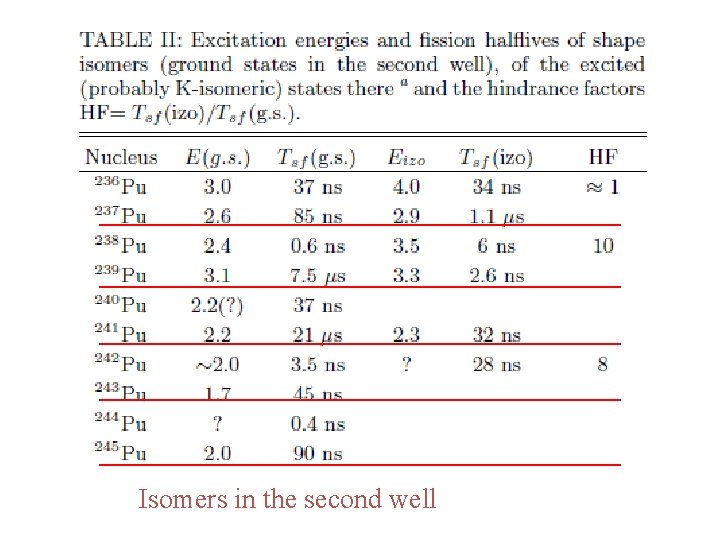
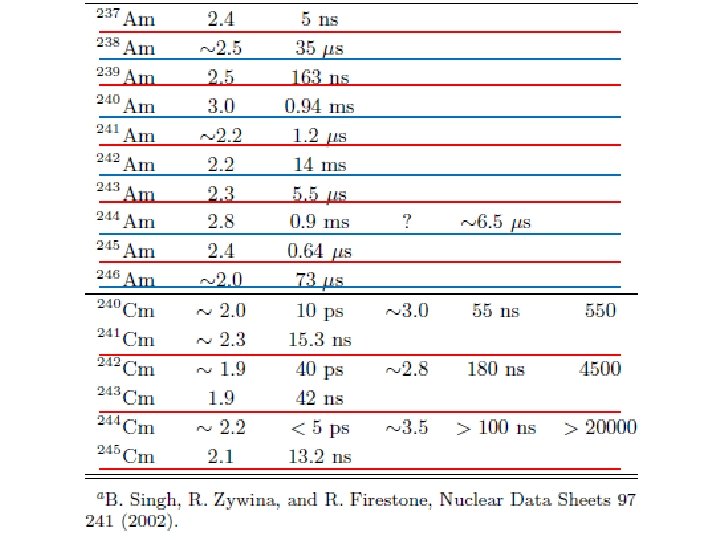
Isomers in the second well


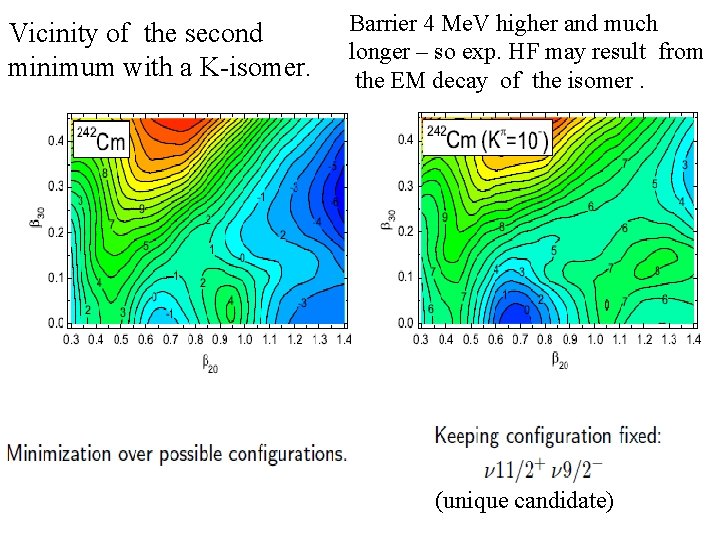
Vicinity of the second minimum with a K-isomer. Barrier 4 Me. V higher and much longer – so exp. HF may result from the EM decay of the isomer. (unique candidate)

Ideas: -Partial release of K quantum number – first barriers are often triaxial; -Consider the minimization of S allowing the pairing gap to vary freely [L. G. Moretto and R. P. Babinet Phys. Lett. 49 B, 147 (1974)]. A. Staszczak, A. Baran, Pomorski & K. Boning found that this decreases the action in Phys. Lett. 161, 227 (1985). Then Yu. A. Lazarev showed in a simple model [Phys. Scripta 35, 255 (1987)] that the action minimization with respect to the gap would reduce (a desired outcome) fission hindrance for odd-A nuclei and isomers. Caveats: -The cranking inertia was used in S; - The gap is related to the Hamiltonian and should be determined by the dynamics before the action is calculated.

Inertia parameter


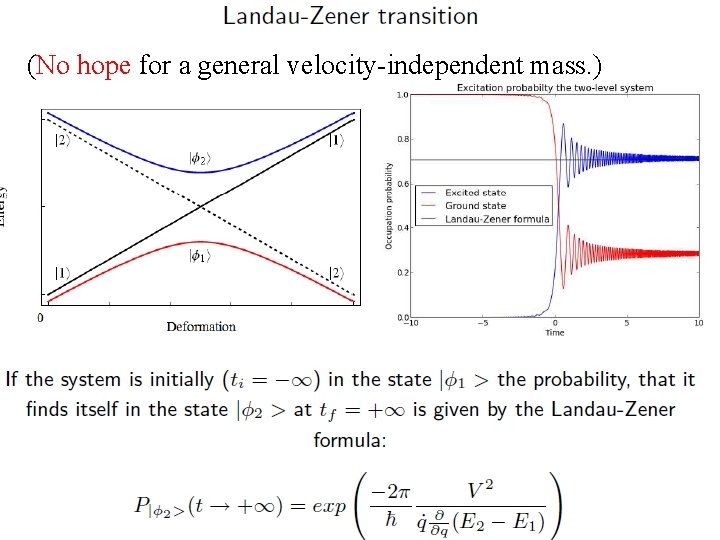
(No hope for a general velocity-independent mass. )

Instanton method In field theory: S. Coleman, Phys. Rev. D 15 (1977) 2929 In nuclear mean-field theory: S. Levit, J. W. Negele and Z. Paltiel, Phys. Rev. C 22 (1980) 1979 • Some simple problems solved: • G. Puddu and J. W. Negele, Phys. Rev. C 35 (1987) 1007 • J. W. Negele, Nucl. Phys. A 502 (1989) 371 c • J. A. Freire, D. P. Arrovas and H. Levine, Phys. Rev. Lett. 79 • (1997) 5054 • J. A. Freire and D. P. Arrovas, Phys. Rev. A 59 (1999) 1461 • J. Skalski, Phys. Rev. A 65 (2002) 033626 Reformulation & Connection to other approaches to the Large Amplitude Collective Motion: J. Skalski, PRC 77, 064610 (2008). The main idea: even if there is no mass, there is action.


Gamow method: motion with imaginary momentum. Formally: In general: the stationary phase approximation to the path-integral expression for the propagator TD variational principle Decay rate proportional to: with S action for the periodic instanton called bounce.


The Eq. (1) without the r. h. s. conserves E and The full Eq. (1) preserves diagonal overlaps, the offdiagonal are equal to zero if they were zero initially. The boundary conditions: This + periodicity: Decay exponent:

Antihermitean part of h = Thouless-Valatin term. Within the density functional method the generic contribution to the antihermitean part of h comes from the current j: (note that: and this differs by a factor (-i) with respect to the real-time TDHF). As a result, the related time-odd contribution to the mean field becomes: and appears as soon as the real parts of start to differ.
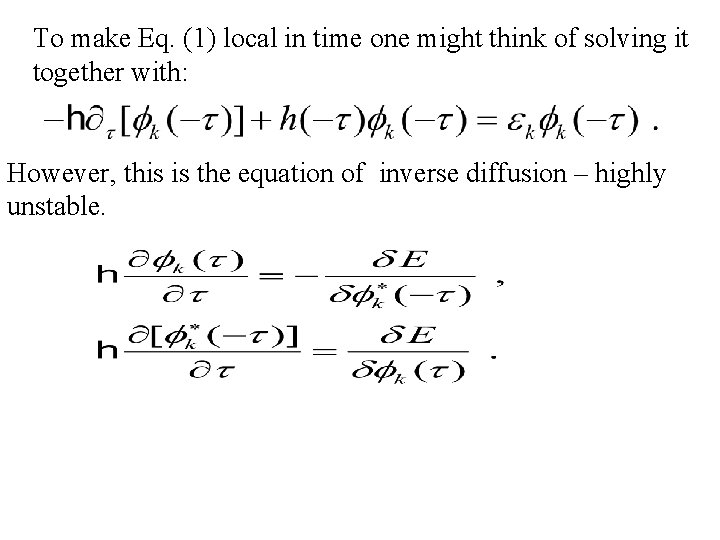
To make Eq. (1) local in time one might think of solving it together with: However, this is the equation of inverse diffusion – highly unstable.

A miracle, by which energy can be constant: there are two sets of Slater determinants: GCM energy kernel on [0, T/2]
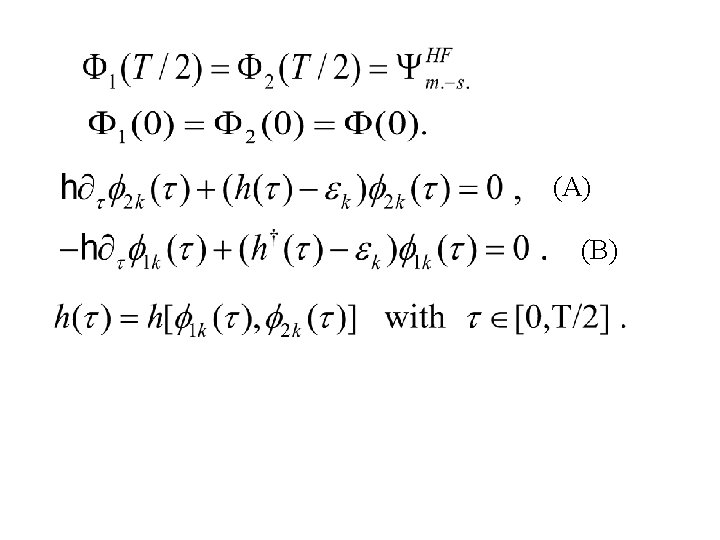

Time-even coordinates and time-odd momenta:

Some similarity to cranking, but the self-consistency changes a lot. Expression for current (time-odd density):

Another representation & adiabatic limit: The analogue of density matrix: but there is no density operator for instanton.

Example: harmonic oscillator with a TD frequency




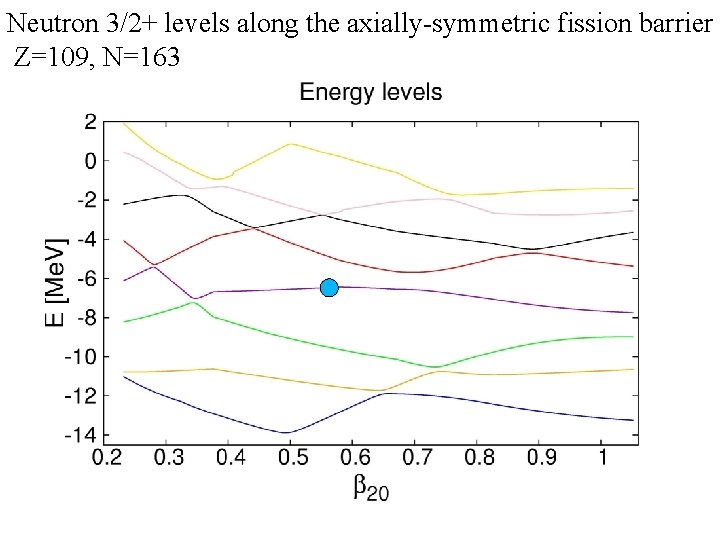
Neutron 3/2+ levels along the axially-symmetric fission barrier Z=109, N=163


Pairing is important → Im. TDHFB; instanton with the smallest action defines the decay rate.

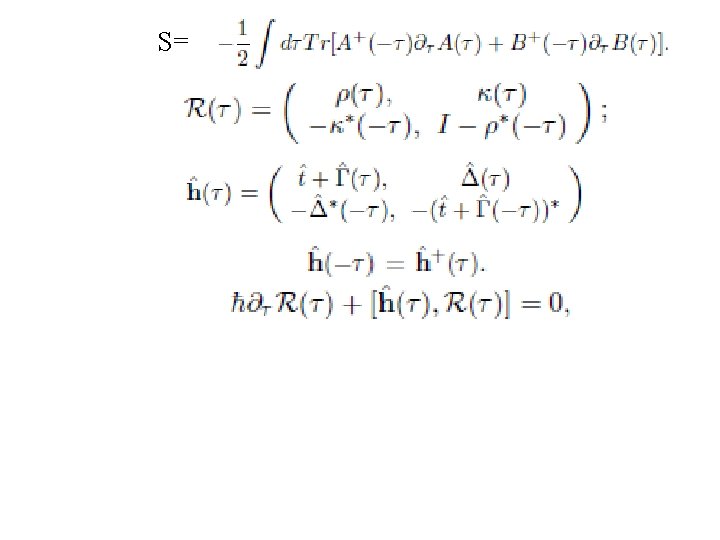
S=

Non-selfconsistent case: if one takes s. p. energies for t+Γ and diagonal ∆ (typical pairing gap), then including time-evolution of the adiabatic basis one has to solve iteratively, self-adjusting ∆ as a function on [-T/2, T/2].

Thus, there is a consistent dynamical equation which determines both pairing delta and action.

Conclusions - Experimental data suggest a mechanism for fission hindrance in both odd-A nuclei and isomers. - Such states can have longer fission half-lives in the SHN region – K may be larger since higher shells are occupied. - The pairing + specialization energy (configuration – preserving) mechanism seems too strong. - The description of fission for odd-A nuclei and isomers is unsatisfactory – it lacks a sound principle. -The instanton method adapted to the mean-field formalism may provide a basis for the minimization of action. - The preliminary, non-selfconsistent studies indicate that the action is well defined for an arbitrary path. - Calculations on paired systems are under way. - Inclusion of the selfconsistency lies ahead.
 Spontaneous fission definition
Spontaneous fission definition Qft
Qft Magdalena jachimowicz
Magdalena jachimowicz Magdalena jachimowicz
Magdalena jachimowicz Piotr jachimowicz
Piotr jachimowicz Unit rate vocabulary
Unit rate vocabulary Ratios guided notes
Ratios guided notes Ratios rates and unit rates
Ratios rates and unit rates Ratios rates and unit rates
Ratios rates and unit rates Who discovered uranium
Who discovered uranium Uranium nuclear fission
Uranium nuclear fission Fission
Fission Nuclear fission formula
Nuclear fission formula Protozoa invertebrates
Protozoa invertebrates Advantage of binary fission
Advantage of binary fission Binary fission vs conjugation
Binary fission vs conjugation A uranium nucleus at rest undergoes fission
A uranium nucleus at rest undergoes fission Fission reactor nuclearcraft
Fission reactor nuclearcraft Nuclear fusion radiation
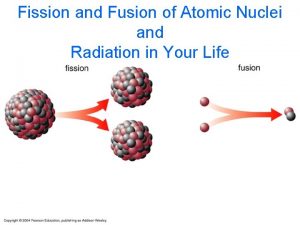
Nuclear fusion radiation Fission vs fusion
Fission vs fusion Fission vs fusion nuclear
Fission vs fusion nuclear Nuclear fission lise meitner
Nuclear fission lise meitner Fission equation
Fission equation Fission definition
Fission definition Fusion or fission
Fusion or fission Spallation neutron source
Spallation neutron source Fission vs fusion energy output
Fission vs fusion energy output Nuclear fission explanation
Nuclear fission explanation Is the sun fusion or fission
Is the sun fusion or fission Betasönderfall
Betasönderfall Nuclear fission and fusion similarities
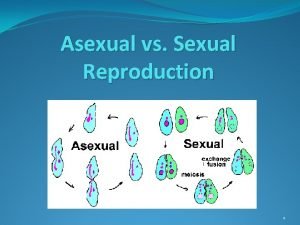
Nuclear fission and fusion similarities Asexual reproduction cell division
Asexual reproduction cell division Uranium atomic mass
Uranium atomic mass Fission equation
Fission equation Geiger counter
Geiger counter Nuclear fission and fusion similarities
Nuclear fission and fusion similarities Fission binaire et mitose
Fission binaire et mitose Advantages of binary fission
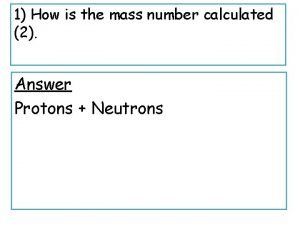
Advantages of binary fission How is mass number calculated
How is mass number calculated