Fractional Statistics of Quantum Particles D P Arovas

Fractional Statistics of Quantum Particles D. P. Arovas, UCSD 7 Pines meeting, Stillwater MN, May 6 -10 2009 Collaborators: Major ideas: Texts: J. R. Schrieffer, F. Wilczek, A. Zee, T. Einarsson, S. L. Sondhi, S. M. Girvin, S. B. Isakov, J. Myrheim, A. P. Polychronakos J. M. Leinaas, J. Myrheim, R. Jackiw, F. Wilczek, M. V. Berry, Y-S. Wu, B. I. Halperin, R. Laughlin, F. D. M. Haldane, N. Read, G. Moore Geometric Phases in Physics Fractional Statistics and Anyon Superconductivity (both World Scientific Press)

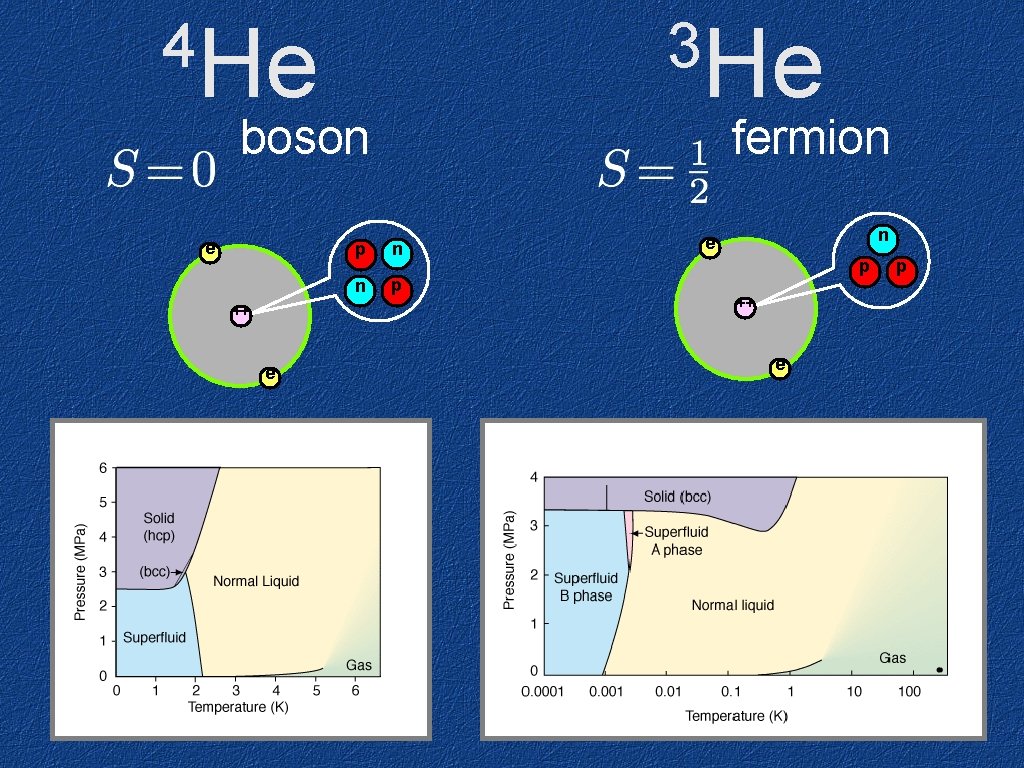
Two classes of quantum particles: bosons gauge matter fermions quarks leptons - symmetric wavefunctions - antisymmetric wavefunctions - real or complex quantum fields - Grassmann quantum fields - condensation - must pair to condense - classical limit: breaks U(1) - no classical analog:

4 He 3 He boson e ++ e fermion p n e p ++ e p

Quantum Mechanics of Identical Particles Is that you, Gertrude? Hamiltonian invariant under label exchange: i. e. where Eigenfunctions of H classified by unitary representations of SN : Only two one-dimensional representations of SN : Bose: Fermi:

Path integral description QM propagator: (manifold) Paths on M are classified by homotopy : and homotopic if YES with { NO smoothly deformable

Path composition ⇒ group structure : π1(M) = “fundamental group” The propagator is expressed as a sum over homotopy classes μ : weight for class μ In order that the composition rule be preserved, the weights χ(μ) must form a unitary representation of π1(M) : Think about the Aharonov-Bohm effect :

Laidlaw and De. Witt (1971) : quantum statistics and path integrals one-particle “base space” configuration space for N distinguishable particles ? for indistinguishables? But. . . not a manifold! how to fix : Then : : disconnected : simply connected : multiply connected N-string braid group Y-S. Wu (1984)

: generated by = = - unitary one-dimensional representations of : - topological phase : change in relative angle - absorb into Lagrangian: with

Charged particle - flux tube composites : (Wilczek, 1982) exchange phase Particles see each other as a source of geometric flux : physical Gauge transformation : statistical multi-valued single-valued Anyon wavefunction :

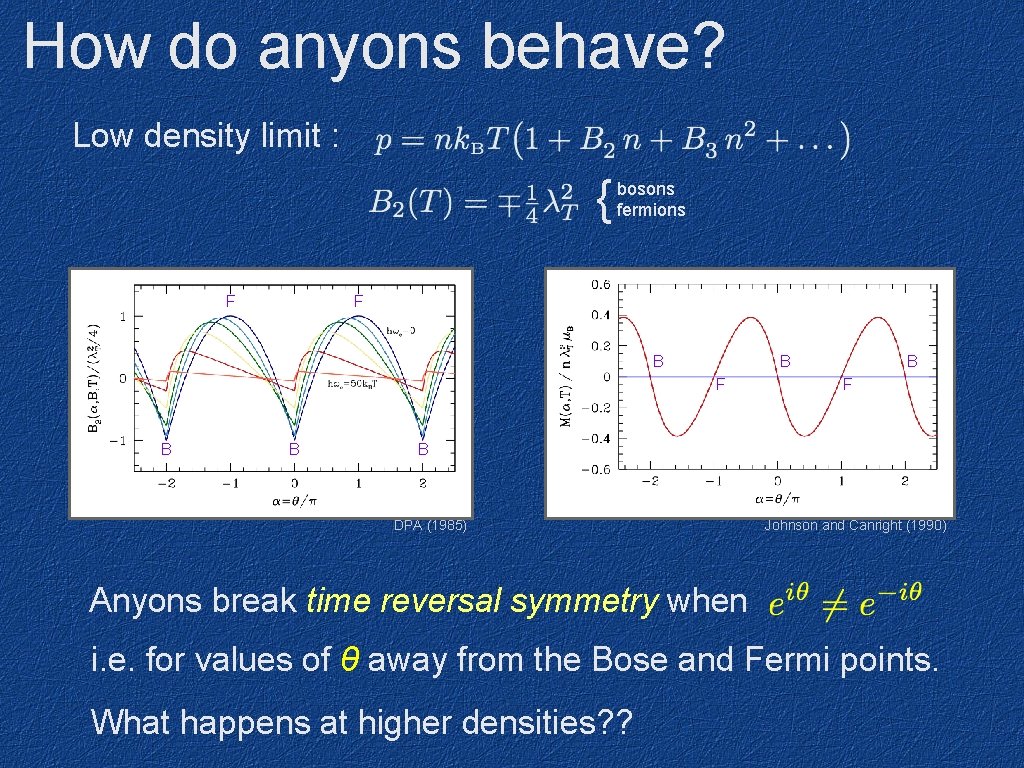
How do anyons behave? Low density limit : { F bosons fermions F B B B F B DPA (1985) Johnson and Canright (1990) Anyons break time reversal symmetry when i. e. for values of θ away from the Bose and Fermi points. What happens at higher densities? ?

Chern-Simons Field Theory and Statistical Transmutation lazy HEP convention: metric Given any theory with a conserved particle current, we can transmute statistics: minimal coupling Chern-Simons term Examples: ordinary matter, skyrmions in O(3) nonlinear σ-model, etc. Integrate out the statistical gauge field via equations of motion: ⇒ linking statistical b-field So we obtain an effective action, Wilczek and Zee (1983) particle density

Anyon Superconductivity fermions plus residual statistical interaction The many body anyon Hamiltonian contains only statistical interactions: The magnetic field experienced by fermion i is Mean field Ansatz : ⇒ Landau levels : filling fraction ⇒ Total energy filled Landau levels ⇒ sound mode : But absence of low-lying particle-hole excitations ⇒ superfluidity! (? )

Anyons in an external magnetic field : Y. Chen et al. (1989) + nth Landau level partially empty + (n+1)th Landau level partially filled system prefers B=0 Meissner effect confirmed by RPA calculations ⇒ A. Fetter et al. (1989)

Signatures of anyon superconductivity Y. Chen et al. (1989) - Zero field Hall effect - reflection of polarized light - local orbital currents - charge inhomogeneities at vortices Unresolved issues Wen and Zee (1989) (not much work since early 1990’s) - route to anyon SC doesn’t hinge on broken U(1) symmetry “spontaneous violation of fact” (Chen et al. ) q even duality treatments of Fisher, Lee, Kane statistics of parent q odd - Pairing? BCS physics? Josephson effect? p even p odd B/F B B/F F

Fractional Quantum Hall Effect Laughlin state at : (1983) Quasihole excitations: Quasihole charge deduced from plasma analogy The Hierarchy - Haldane / Halperin (1983 / 1984) - condensation of quasiholes/quasiparticles - Halperin : “pseudo-wavefunction” satisfying fractional statistics

Geometric phases M. V. Berry (1984) Adiabatic evolution solution to SE (projected) Complete path : adiabatic WF where Evolution of degenerate levels ➙ nonabelian structure : Path : where Wilczek and Zee (1984)

Adiabatic quasihole statistics DPA, Schrieffer, Wilczek (1984) - Compute parameters in adiabatic effective Lagrangian quasihole charge from Aharonov-Bohm phase : This establishes in agreement with Laughlin For statistics, examine two quasiholes: ⇒ Exchange phase is then

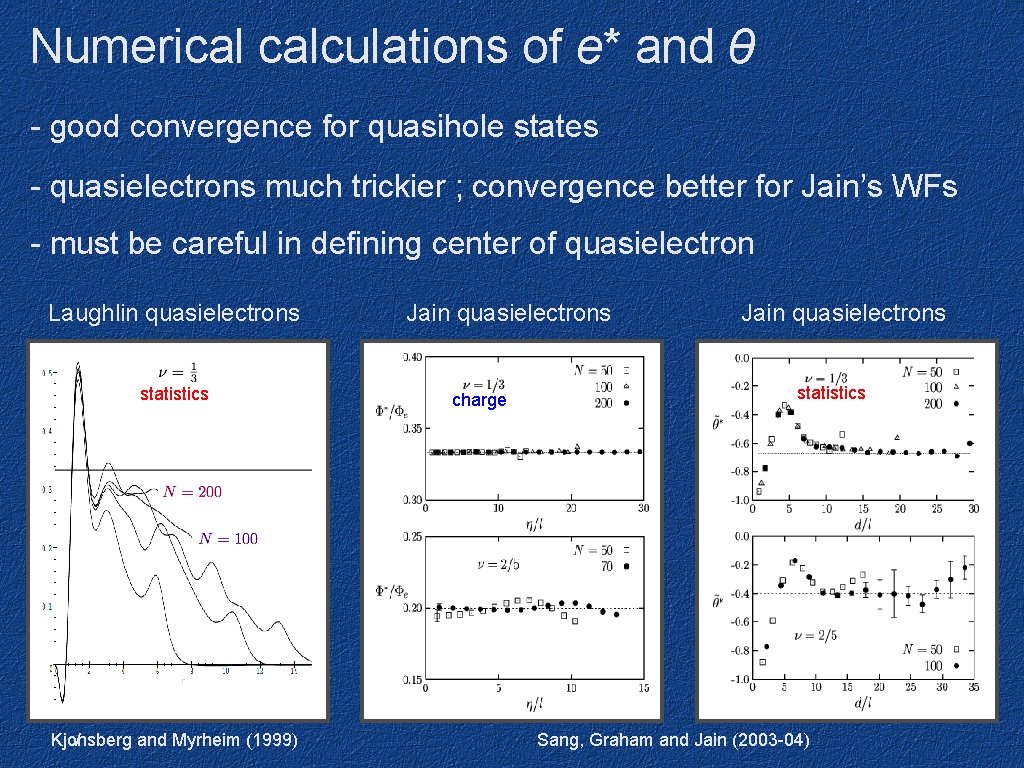
Numerical calculations of e* and θ - good convergence for quasihole states - quasielectrons much trickier ; convergence better for Jain’s WFs - must be careful in defining center of quasielectron Laughlin quasielectrons statistics Kjo nsberg and Myrheim (1999) Jain quasielectrons charge Jain quasielectrons statistics Sang, Graham and Jain (2003 -04)

Effective field theory for the FQHE Girvin and Mac. Donald (1987) ; Zhang, Hansson, and Kivelson (1989) ; Read (1989) Basic idea : fermions = bosons + Extremize the action : Solution : , , incompressible quantum liquid with

Quasiparticle statistics in the CSGL theory - quasiparticles are vortices in the bosonic field , - ‘duality’ transformation to quasiparticle variables reveals fractional statistics with new CS term!

Statistics and interferometry : Stern (2008) Fabry-Perot relative phase : D S changing B will nucleate bulk quasiholes, resulting in detectable phase interference Mach-Zehnder D relative phase : phase interference depends on number of quasiparticles which previously tunneled S - dependence ⇒ fractional statistics

Nonabelions Moore and Read (1991) Nayak and Wilczek (1996) Read and Green (2000) Ivanov (2001) quasihole creator - For M Laughlin quasiholes, one state : - At , there are states with quasiholes : with - This leads to a very rich braiding structure, involving higher-dimensional representations of the braid group - The degrees of freedom are essentially nonlocal, and are associated with Majorana fermions - There is a remarkable connection with vortices in (px+ipy)-wave superconductors - These states hold promise for fault-tolerant quantum computation

Exclusion statistics Haldane (1991) = # of quasiparticles of species = # of states available to qp Model for exclusion statistics : FQHE quasiparticles obey fractional exclusion statistics :

Key Points ✸ In d=2, a one-parameter (θ) family of quantum statistics exists between Bose (θ=0) and Fermi (θ=π), with broken T in between ✸ Anyons behave as charge-flux composites (phases from A-B effect) ✸ Two equivalent descriptions : (i) bosons or fermions with statistical vector potential (ii) multi-valued wavefunctions with no statistical interaction ✸ Beautiful effective field theory description via Chern-Simons term ✸ The anyon gas at is believed to be a superconductor ✸ FQHE quasiparticles have fractional charge and statistics ✸ Exotic nonabelian statistics at ✸ Related to exclusion statistics (Haldane), but phases essential