Fractional Cascading Fractional Cascading I A Data Structuring

Fractional Cascading • Fractional Cascading I: A Data Structuring Technique • Fractional Cascading II: Applications [Chazaelle & Guibas 1986] • Dynamic Fractional Cascading [Mellhorn & Naher 1990] Elik Etzion January 2002

Agenda Preview Formal problem definition & Final results Example Application Intersecting a polygonal path with a line Data structure & Algorithm description Time & Space complexity analysis Dynamization

Preview The problem: Iterative search in sorted lists Examples: Look up a word in different dictionaries Geometric retrieval problems The solution: Fractional Cascading Correlate the lists in a way that every search uses the results of the previous search

Formal Definition U – an ordered set G = (V, E) – Catalog Graph undirected for each v V C(v) U catalog of v For each e E R(e) = [ l(e) , r(e) ] range of e locally bounded degree d v V and k U there at most d edges e = (v, w) with k R(e) [22, 50] [2, 7] [5, 15] [20, 27] Degree = 4 Locally bounded degree = 2

Formal Definition - operations Query Input : k U , G` = (V`, E`) connected sub-tree of G , e E` k R(e) Output for each v V` x C(v) such that x is the successor of k in C(v) Deletion given a key k C(v) and its position in C(v), delete k from C(v) Insertion given a key k U and its successor in C(v), insert k into C(v)

Results n |V| , Space: O(N + |E|) Time: Query Insert / Delete Trivial nlog. N 1 Static/Semi. Dynamic log(N + |E|) + n 1 log(N + |E|) + nloglog (N + |E|) amortized

Example application Problem Input: Polygonal path P, Arbitrary query line l Output: intersections of P & l Solution complexity Trivial Using FC space: time: O(n) O(nlogn) O((k+1)log[n/(k+1)]) k – number of intersections reported

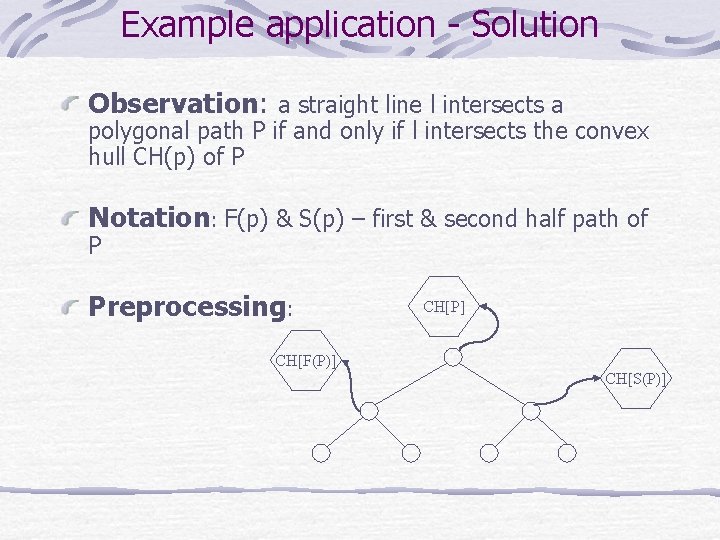
Example application - Solution Observation: a straight line l intersects a polygonal path P if and only if l intersects the convex hull CH(p) of P Notation: F(p) & S(p) – first & second half path of P Preprocessing: CH[P] CH[F(P)] CH[S(P)]

Example application - Algorithm Intersect( P , l ) { if |P| = 1 then compute P l directly else if l doesn’t intersect CH(p) then exit else { Intersect ( F(p) , l ) Intersect ( S(p) , l ) } }

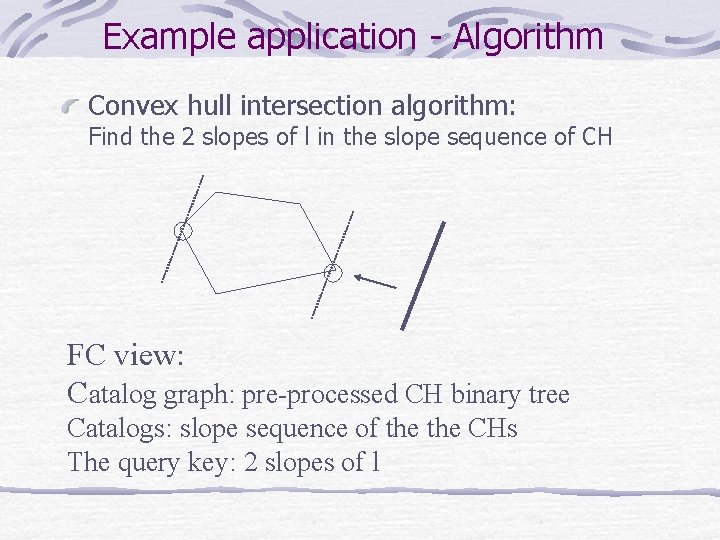
Example application - Algorithm Convex hull intersection algorithm: Find the 2 slopes of l in the slope sequence of CH FC view: Catalog graph: pre-processed CH binary tree Catalogs: slope sequence of the CHs The query key: 2 slopes of l

Example application - Complexity Space O(nlogn) - each edge participates in at most logn CHs Time (static) O(logn + size of sub tree actually visited) O((k+1)log[n/(k+1)])

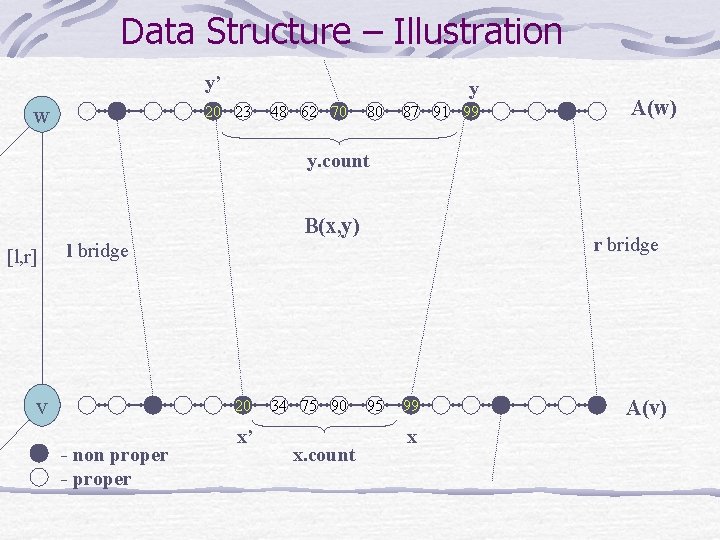
Data Structure – Illustration y’ w y 20 23 48 62 70 80 87 91 99 A(w) y. count B(x, y) [l, r] r bridge l bridge v 20 - non proper - proper x’ 34 75 90 x. count 95 99 x A(v)

Data Structure - Definitions For each node v A(v) C(v) – augmented catalog implemented as a doubly linked list of records C(v) contains proper elements A(v) – C(v) contains non-proper elements Record members: key, next, prev, kind special n. p members: target – node of G incident to v pointer – pointer to a np element in A(x. target) (the other end of the bridge) count – number of elements until the previous bridge in_S – is in a non- balanced block

Bridges & Blocks (x, y)- a bridge between nodes v & w x A(v) – C(v) y A(w) – C(w) x. pointer = y y. pointer = x x. target = w y. target = v x. key = y. key x. kind = y. kind = non-proper Every edge e(v, w) has at list 2 bridges x. key=y. key = l(e) , x. key = y. key = r(e) Block B(x, y) A(v) A(w) the elements between (x, y) bridge and its neighbor bridge between v & w |B(x, y)| = x. count + y. count

FCQuery (G, G’, k ) (V 1, V 2. . Vn) = order of nodes in G’ aug_succ = Binary. Search( A(V 1), k ) successor[1] = Find. Proper(A(V 1), aug_succ) for i = 2. . n aug_succ = FCSearch(Vi, k, succssesor[i-1]) successor[i] = Find. Proper(A(Vi), aug_succ) return successor[1. . n]

FCSearch & Find. Proper FCSearch ( w, k, x ) x’ = x while x’. target != w do x 1 = x’. next y = x’. pointer While y. pred. key k do y= y. pred return y Find. Proper in the static case implemented in O(1) time using a pointer from each non-proper element to its proper successor

Block Size Tradeoff Small blocks increase space complexity but decrease time complexity Large blocks increase time complexity but decrease space complexity Block Invariant There are tow constants a, b with a b such that for all blocks B(x, y) holds: |B(x, y)| b |B(x, y)| a or B(x, y) is the only block between A(x. target) and A(y. target)

Block Lemma Let Then |S| 3 N+12|E| Proof …

Complexity Analysis (static) Space Linear in the size of the catalog graph according to the Block Lemma Time Find. Proper O( 1 ) FCSearch O( 1 ) block size is constant Binary. Search O ( log(|A(V 1)|) ) = O ( log(N + |E|) ) FCQuery – O (log(N + |E|) + n )

Dynamization Challenges Find. Proper can’t be implemented simply by using a pointer from each non-proper element to its proper successor Insertions & Deletions violate the Block Invariant Solution Data Structure based on. Van Emde Boas Priority Queue Block rebalancing

Union- Split DS Find. Proper Input: a pointer to some item x Output: a pointer to a proper item y such that all the items between x & y are non-proper ( y is the proper successor of x) ADD Input: a pointer to some item x Effect: adds a non-proper item immediately before x Erase Input: a pointer to a non-proper item x Delete x Union Input: a pointer to a non-proper item x Effect: change the mark of x to proper Split Input: a pointer to a proper item x Effect: change the mark of x to non-proper

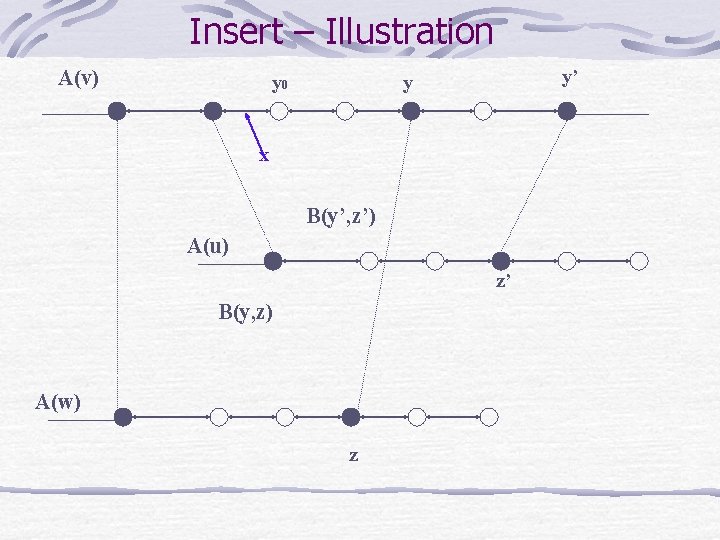
Insert – Illustration A(v) y 0 y’ y x B(y’, z’) A(u) z’ B(y, z) A(w) z

Insert Algorithm Insert (x , y 0) ADD( x , y 0 ) if x. kind = proper then UNION(x) insert x into the doubly linked list before y 0 y = y 0 , A = do b times w = y. target if ( y. kind = non-proper and w A and x. key R(v, w) ) A = A {w} y. count++ z = y. pointer if ( y. In_S = false and y. count + z. count > b) S = S {B(y, z)} y. In_s = true , z. In_S = true y = y. next

Delete Algorithm Delete (x) if x. kind = proper then SPLIT(x) DELETE(x) remove x from the doubly linked y = x. next , A = do b times w = y. target if ( y. kind = non-proper and w A and x. key R(v, w) ) A = A {w} y. count-z = y. pointer if ( y. In_S = false and y. count + z. count < a and B(z, y) isn’t the only block between v and w ) S = S {B(y, z)} y. In_s = true , z. In_S = true y = y. next

Balance Algorithm For each block B(x, y) S do l = compute the size of B(x, y) by running to the previous parallel bridge [ O(l) ] if ( l > b) divide B(x, y) into 3 l/b + 1 parts by inserting 2* 3 l/b non-proper elements [6 l/b O(INSERT) ] else if ( l < a ) concatenate B(x, y) with its right neighbor block B(x’, y’) by deleting the (x, y) bridge [O(ERASE)] check if B(x’, y’) S by scanning b elements until reaching the (x’, y’) bridge and checking x’. In_s flag [O(b)] // if not reached then B(x’, y’) S if B(x’, y’) S x’. count += x. count , y’. count += y. count if (x’. count > b) S = S {B(x’, y’)} else S = S – B(x, y)

Complexity Analysis (Dynamic) Union – Split DS for n elements complexity Space: o (n) Time : FIND, Union & split: O(loglogn) worst case ADD, Erase: O(loglogn) amortized ADD/ ERASE in semi-dynamic: O(1) FC complexity Space: Remains Linear in the size of the catalog graph because the block invariant is kept by rebalancing Time: Find. Proper: O( log(N + |E|) ) FCSearch: O( 1 ) Binary. Search O ( log(N + |E|) ) FCQuery – O (log(N + |E|) + n log(N + |E|) ) Insert/Delete - O( log(N + |E|) ) or O (1) or semidynamic Balance – O ( log(N + |E|) ) amortized (complex proof)