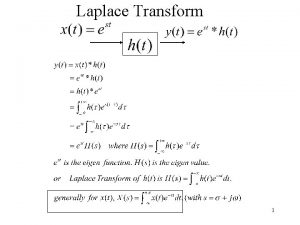Fourier Transform FT EET 206 ELECTRIC CIRCUIT II

















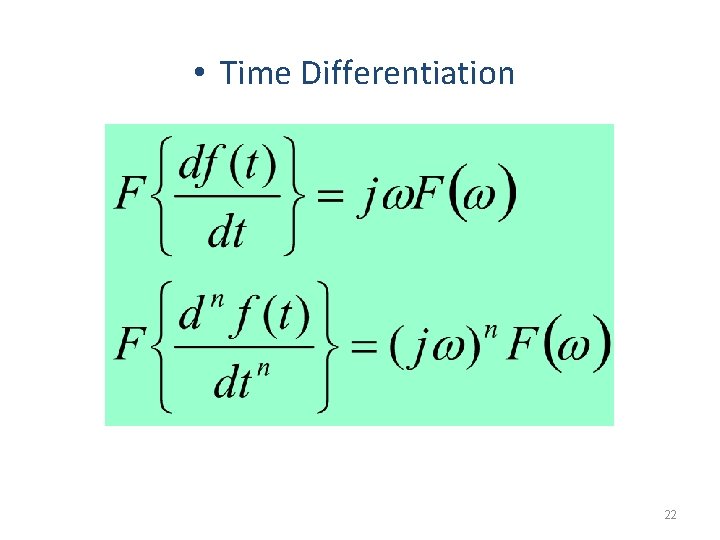


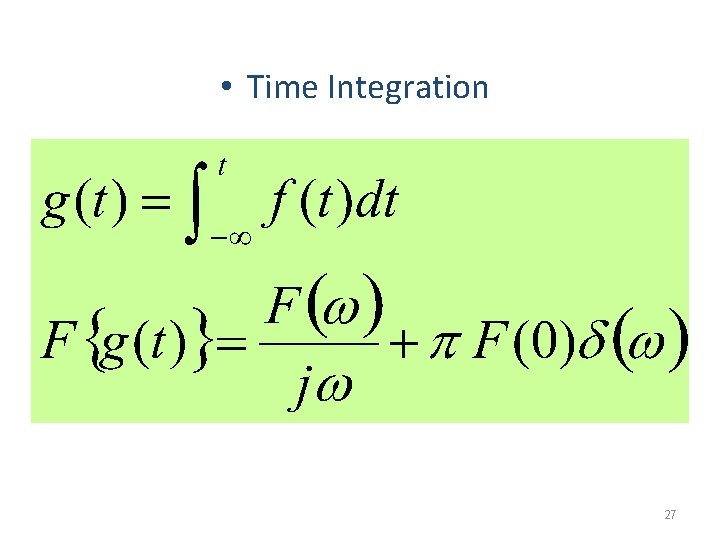








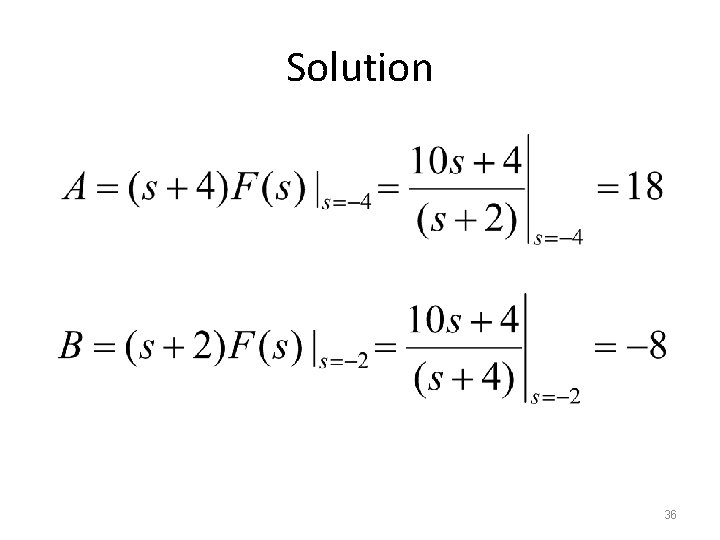

- Slides: 37

Fourier Transform (FT) EET 206 – ELECTRIC CIRCUIT II 1

CONTENTS • • • Introduction to Fourier transforms (FT) Comparison to Laplace T and Phasors Definition of Fourier Transform Fourier transforms of Basic Functions Properties of the Fourier Transforms Circuit applications using Fourier Transforms 2

Introduction To Fourier Transform Recall that: • Fourier Series enable us to represent a periodic function as a sum of sinusoids Now know that : • Fourier Transform (FT) is integral representation of a non periodic function Therefore: • In another words, FT is an integral transformation of f(t) from the time domain to the frequency domain 3

Comparison to Laplace Transform and Phasors • FT, Laplace T and phasors are all in frequency domain, where we can transform back to time domain form of the final solution by using inverse methods • Phasors is only applicable when input is sinusoidal periodic function, but FT can be used for non periodic and non sinusoidal function • Laplace only works for t > 0 with initial condition being stated, but FT can be used for t < 0 as well as for t > 0 4

Definition of Fourier Transforms 5

Inverse Fourier Transforms 6

FT of Basic Functions • We will show to obtain the FT of some basic functions using the (integral) definition of FT. • For more complex functions where the integral becomes tedious, we may temporarily replace jω by s and then replace back s with jω at the end. • The inverse transform may be obtained using partial fraction and the table as in Laplace T. 7

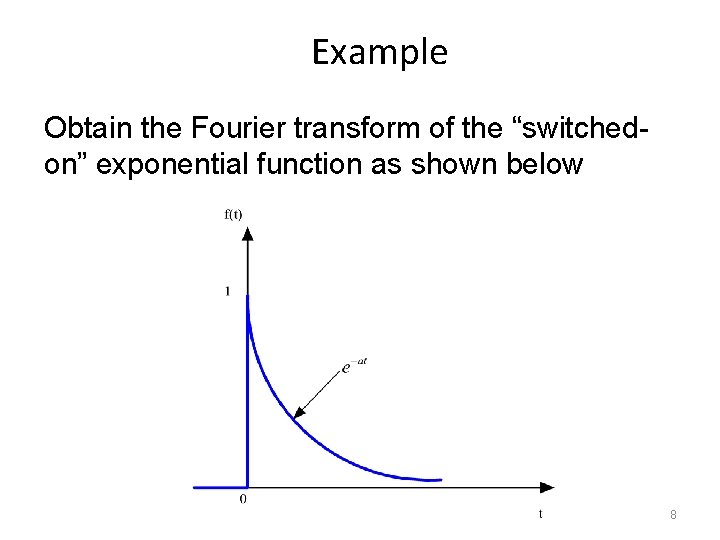
Example Obtain the Fourier transform of the “switchedon” exponential function as shown below 8

Solution: Given function is: 9

Its Fourier Transform is: 10

Example 11

Solution: 12

Example 13

Solution: 14

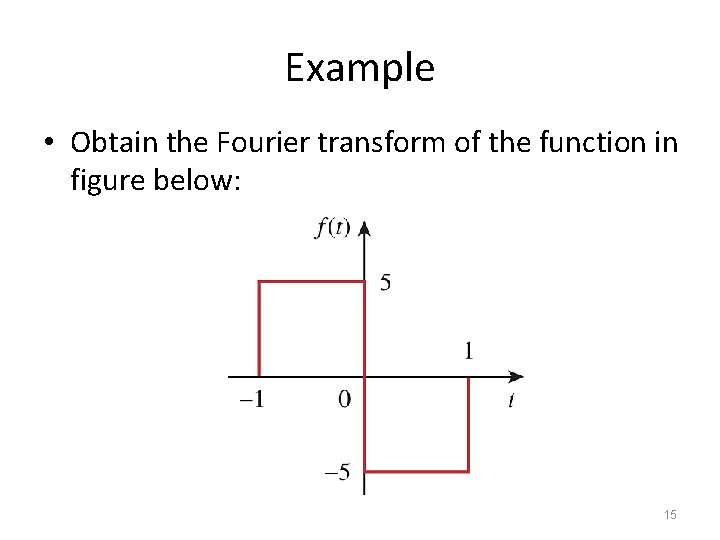
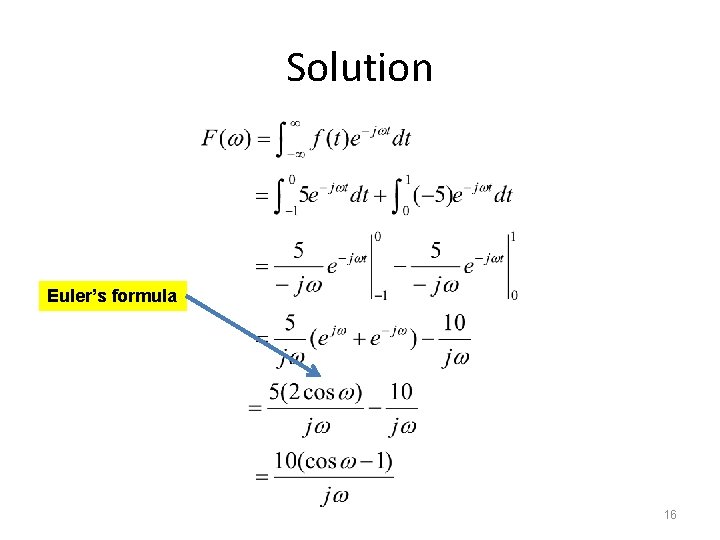
Example • Obtain the Fourier transform of the function in figure below: 15

Solution Euler’s formula 16

Example • Determine the Fourier transform of: g(t) = 4 u(t - 1) – 4 u(t - 2) • Solution: 17

Properties of Fourier Transforms 18

Properties of Fourier Transforms 19

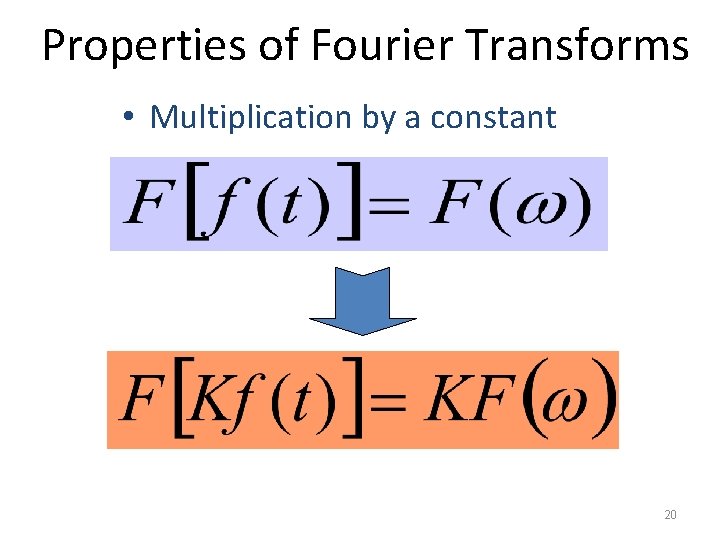
Properties of Fourier Transforms • Multiplication by a constant 20

• Addition and subtraction 21
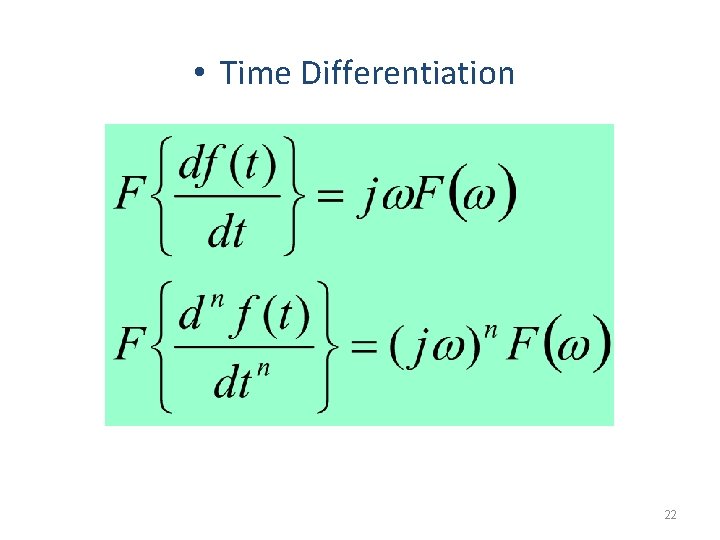
• Time Differentiation 22

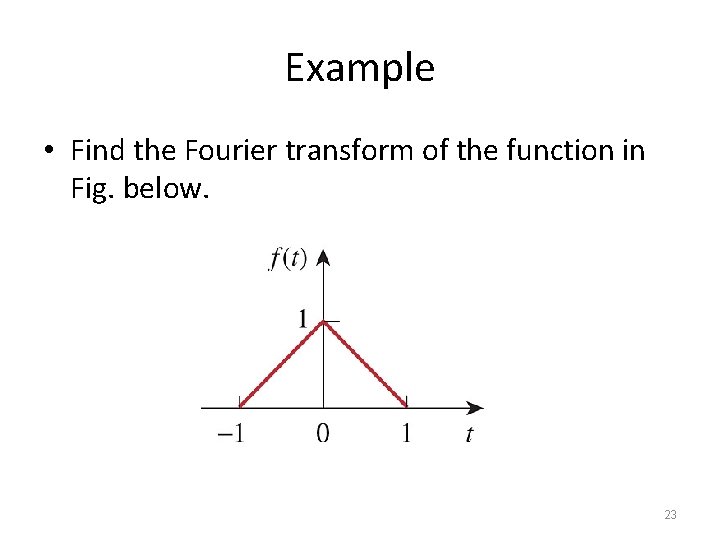
Example • Find the Fourier transform of the function in Fig. below. 23

Solution • It is much easier to find the FT using the derivative property. • The first derivative: Now: f(t) = u(t+1) – u(t) – [u(t) – u(t-1)] = u(t+1) – u(t) + u(t-1)] = u(t+1) – 2 u(t) + u(t-1)] 24

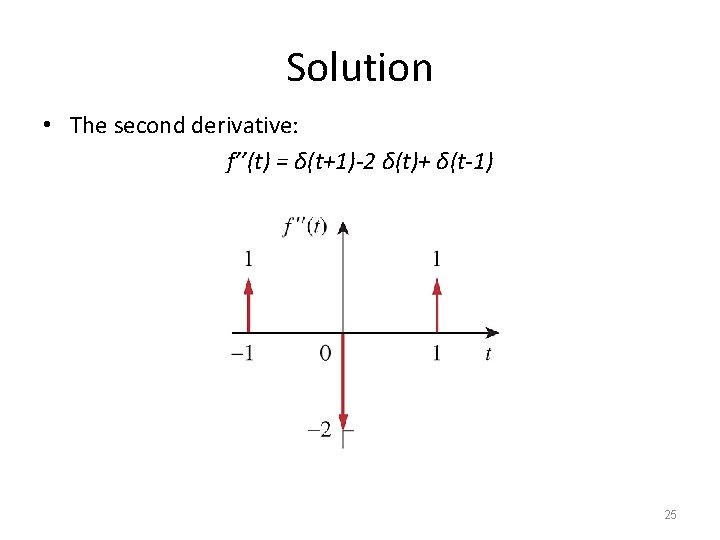
Solution • The second derivative: f’’(t) = δ(t+1)-2 δ(t)+ δ(t-1) 25

Solution • Using the time differentiation property: (jω)2 F(ω) = ejω-2+e-jω = -2+2 cosω So, F(ω) = 2(1 -cosω) ω2 26
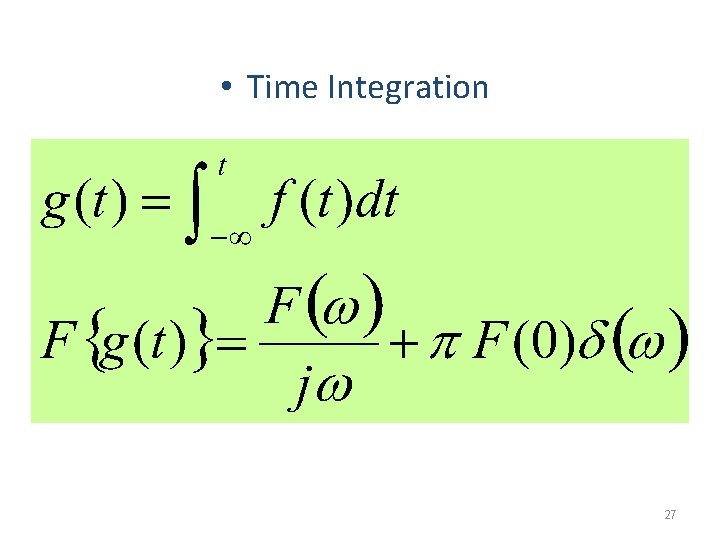
• Time Integration 27

• Time Scaling 28

• Time shifting Delay in the time domain corresponds to the phase shift in the frequency domain 29

• Frequency shifting Frequency shift in the frequency domain adds phase shift to the time domain 30

• Modulation 31

• Convolution in frequency domain: 32

• Convolution in time domain 33

Example on Finding Inverse FT: • Determine the inverse Fourier Transforms (FT) for the function below: 34

Solution To avoid complex algebra, we can replace jω with s for the moment. Using partial fraction 35
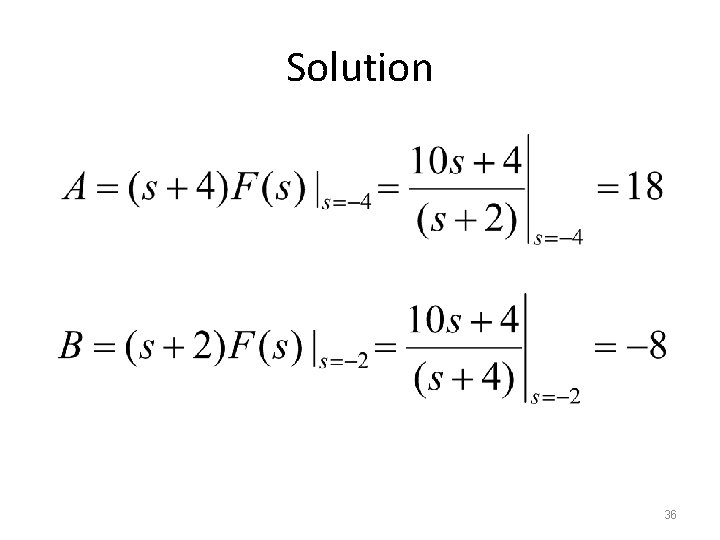
Solution 36

• A and B value: • Then replace back s = jω • Inverting the frequency domain to time domain, we get the inverse transform: 37
 Electric circuit analysis using laplace transform
Electric circuit analysis using laplace transform A suitable electric pump in an electric circuit is a
A suitable electric pump in an electric circuit is a Image processing and analysis stan birchfield pdf
Image processing and analysis stan birchfield pdf Series de fourier
Series de fourier Fourier transform in image processing
Fourier transform in image processing Inverse fourier transform
Inverse fourier transform Rect t/2
Rect t/2 Fourier transform complex analysis
Fourier transform complex analysis Fourier transform
Fourier transform Ctft properties
Ctft properties Fourier transform of gaussian
Fourier transform of gaussian Fourier transform pair
Fourier transform pair Relation between laplace and fourier transform
Relation between laplace and fourier transform Half range fourier series
Half range fourier series Inverse fisher transform
Inverse fisher transform Laplace table transform
Laplace table transform Fourier transform table
Fourier transform table Rect(t-1/2)
Rect(t-1/2) Discrete fourier transform
Discrete fourier transform Fourier transform
Fourier transform Discrete fourier transform
Discrete fourier transform Frft meaning
Frft meaning Fourier transform seismic
Fourier transform seismic 2 pi f t
2 pi f t Chirped pulse fourier transform microwave spectroscopy
Chirped pulse fourier transform microwave spectroscopy Fourier transform formula
Fourier transform formula Fast fourier transform in r
Fast fourier transform in r Delta function fourier transform
Delta function fourier transform Windowed fourier transform
Windowed fourier transform Inverse fourier transform formula
Inverse fourier transform formula Fourier transform of impulse signal
Fourier transform of impulse signal Fourier transform of ramp function
Fourier transform of ramp function Fourier transform is defined for
Fourier transform is defined for Applications of fourier transform
Applications of fourier transform Short time fourier transform
Short time fourier transform Short time fourier transform applications
Short time fourier transform applications Inverse fourier transform
Inverse fourier transform Fast fourier transform java
Fast fourier transform java