Final Review List of Logical Equivalences p T

Final Review

List of Logical Equivalences p T p; p F p Identity Laws p T T; p F F Domination Laws p p p; p p p Idempotent Laws ( p) p Double Negation Law p q q p; p q q p Commutative Laws (p q) r p (q r); (p q) r p (q r) Associative Laws

List of Equivalences p (q r) (p q) (p r) Distribution Laws (p q) ( p q) De Morgan’s Laws p p T p p F (p q) ( p q) Miscellaneous Or Tautology And Contradiction Implication Equivalence p q (p q) (q p) Biconditional Equivalence

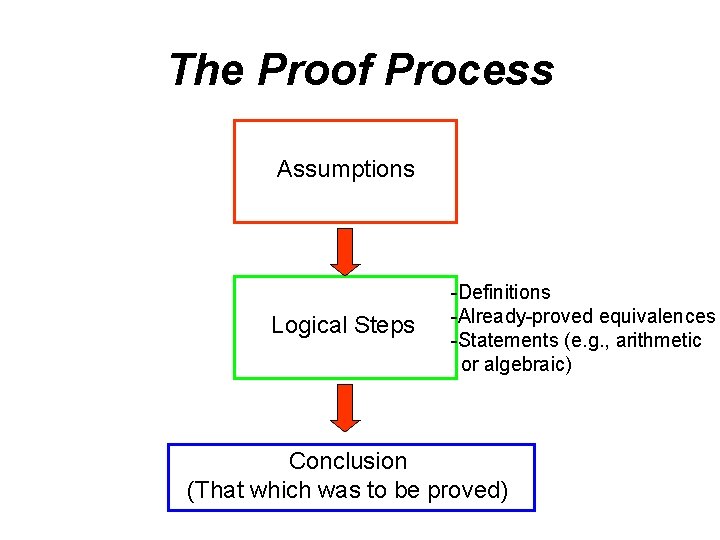
The Proof Process Assumptions Logical Steps -Definitions -Already-proved equivalences -Statements (e. g. , arithmetic or algebraic) Conclusion (That which was to be proved)

Prove: (p q) q p q (p q) q q (p q) (q p) (q q) (q p) T q p p q Left-Hand Statement Commutative Distributive Or Tautology Identity Commutative Begin with exactly the left-hand side statement End with exactly what is on the right Justify EVERY step with a logical equivalence

Predicate Calculus: Quantifiers Universe of Discourse, U: The domain of a variable in a propositional function. Universal Quantification of P(x) is the proposition: “P(x) is true for all values of x in U. ” Existential Quantification of P(x) is the proposition: “There exists an element, x, in U such that P(x) is true. ”

Universal Quantification of P(x) x. P(x) “for all x P(x)” “for every x P(x)” Defined as: P(x 0) P(x 1) P(x 2) P(x 3) . . . for all xi in U Example: Let P(x) denote x 2 x If U is x such that 0 < x < 1 then x. P(x) is false. If U is x such that 1 < x then x. P(x) is true.

Existential Quantification of P(x) x. P(x) “there is an x such that P(x)” “there is at least one x such that P(x)” “there exists at least one x such that P(x)” Defined as: P(x 0) P(x 1) P(x 2) P(x 3) . . . for all xi in U Example: Let P(x) denote x 2 x If U is x such that 0 < x 1 then x. P(x) is true. If U is x such that x < 1 then x. P(x) is true.

Quantifiers x. P(x) • True when P(x) is true for every x. • False if there is an x for which P(x) is false. x. P(x) • True if there exists an x for which P(x) is true. • False if P(x) is false for every x.

Negation (it is not the case) x. P(x) equivalent to x P(x) • True when P(x) is false for every x • False if there is an x for which P(x) is true. x. P(x) is equivalent to x P(x) • True if there exists an x for which P(x) is false. • False if P(x) is true for every x.

Examples 2 a Let T(a, b) denote the propositional function “a trusts b. ” Let U be the set of all people in the world. Everybody trusts Bob. x. T(x, Bob) Could also say: x U T(x, Bob) denotes membership Bob trusts somebody. x. T(Bob, x)

Examples 2 b Alice trusts herself. T(Alice, Alice) Alice trusts nobody. x T(Alice, x) Carol trusts everyone trusted by David. x(T(David, x) T(Carol, x)) Everyone trusts somebody. x y T(x, y)

Quantification of Two Variables (read left to right) x y. P(x, y) or y x. P(x, y) • True when P(x, y) is true for every pair x, y. • False if there is a pair x, y for which P(x, y) is false. x y. P(x, y) or y x. P(x, y) True if there is a pair x, y for which P(x, y) is true. False if P(x, y) is false for every pair x, y.

Quantification of Two Variables x y. P(x, y) • True when for every x there is a y for which P(x, y) is true. (in this case y can depend on x) • False if there is an x such that P(x, y) is false for every y. y x. P(x, y) • True if there is a y for which P(x, y) is true for every x. (i. e. , true for a particular y regardless (or independent) of x) • False if for every y there is an x for which P(x, y) is false. Note that order matters here In particular, if y x. P(x, y) is true, then x y. P(x, y) is true. However, if x y. P(x, y) is true, it is not necessary that y x. P(x, y) is true.

Examples 3 a Let L(x, y) be the statement “x loves y” where U for both x and y is the set of all people in the world. Everybody loves Jerry. x. L(x, Jerry) Everybody loves somebody. x y. L(x, y) There is somebody whom everybody loves. y x. L(x, y)

Examples 3 b 1 There is somebody whom Lydia does not love. x L(Lydia, x) Nobody loves everybody. (For each person there is at least one person they do not love. ) x y L(x, y) There is somebody (one or more) whom nobody loves y x L(x, y)

Basic Number Theory Definitions • • • from Chapter 2 Z = Set of all Integers Z+ = Set of all Positive Integers N = Set of Natural Numbers (Z+ and Zero) R = Set of Real Numbers Addition and multiplication on integers produce integers. (a, b Z) [(a+b) Z] [(ab) Z]

Number Theory Defs (cont. ) • • • = “such that” n is even is defined as k Z n = 2 k n is odd is defined as k Z n = 2 k+1 x is rational is defined as a, b Z x = a/b, b 0 x is irrational is defined as a, b Z x = a/b, b 0 or a, b Z, x a/b, b 0 p Z+ is prime means that the only positive factors of p are p and 1. If p is not prime we say it is composite.

Methods of Proof p q (Example: if n is even, then n 2 is even) • Direct proof: Assume p is true and use a series of previously proven statements to show that q is true. • Indirect proof: Show q p is true (contrapositive), using any proof technique (usually direct proof). • Proof by contradiction: Assume negation of what you are trying to prove (p q). Show that this leads to a contradiction.

Example of an Indirect Proof Prove: If n 3 is even, then n is even. Proof: The contrapositive of “If n 3 is even, then n is even” is “If n is odd, then n 3 is odd. ” If the contrapositive is true then the original statement must be true. Assume n is odd. Then k Z n = 2 k+1. It follows that n 3 = (2 k+1)3 = 8 k 3+8 k 2+4 k+1 = 2(4 k 3+4 k 2+2 k)+1. (4 k 3+4 k 2+2 k) is an integer. Therefore n 3 is 1 plus an even integer. Therefore n 3 is odd. Assumption, Definition, Arithmetic, Conclusion

Example: Proof by Contradiction Prove: The sum of an irrational number and a rational number is irrational. Proof: Let q be an irrational number and r be a rational number. Assume that their sum is rational, i. e. , q+r=s where s is a rational number. Then q = s-r. But by our previous proof the sum of two rational numbers must be rational, so we have an irrational number on the left equal to a rational number on the right. This is a contradiction. Therefore q+r can’t be rational and must be irrational.

Structure of Proof by Contradiction • Basic idea is to assume that the opposite of what you are trying to prove is true and show that it results in a violation of one of your initial assumptions. • In the previous proof we showed that assuming that the sum of a rational number and an irrational number is rational and showed that it resulted in the impossible conclusion that a number could be rational and irrational at the same time. (It can be put in a form that implies n n is true, which is a contradiction. )

Approaches to Set Proofs • Membership tables (similar to truth tables) • Convert to a problem in propositional logic, prove, then convert back • Use set identities for a tabular proof (similar to what we did for the propositional logic examples but using set identities) • Do a logical argument (similar to what we did for the number theory examples)

Prove (A B) = B (A B) = {x | x (A B)} Set builder notation = {x | x (A B)} Def of = {x | (x A x B)} Def of x 2 and Def of complement = {x | (x B x A )} Commutative x 2 = {x | (x B (x A )} Distributive = {x | (x B T } Or tautology = {x | (x B } Identity =B Set Builder notation

Prove (A B) = B (Using Set Identities) (A B) = (B A) =B (A A) =B U =B Commutative Law x 2 Distributive Law Definition of U Identity Law

Prove (A B) = B Proof: We must show that (A B) B and that B (A B). First we will show that (A B) B. Let e be an arbitrary element of (A B). Then either e (A B) or e (A B). If e (A B), then e B and e A. In either case e B.

Prove (A B) = B Now we will show that B (A B). Let e be an arbitrary element of B. Then either e A B or e A B. Since e is in one or the other, then e (A B).

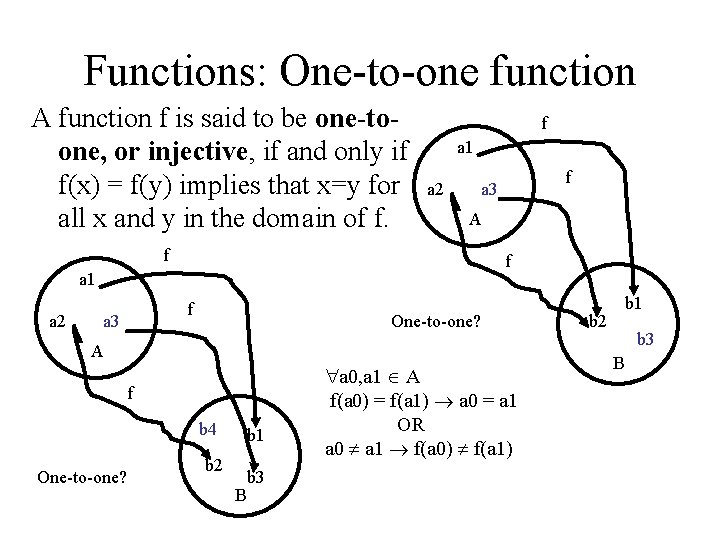
Functions: One-to-one function A function f is said to be one-toone, or injective, if and only if f(x) = f(y) implies that x=y for all x and y in the domain of f. f a 1 a 2 A f f a 1 a 2 f a 3 One-to-one? A f b 4 One-to-one? b 1 b 2 B b 3 a 0, a 1 A f(a 0) = f(a 1) a 0 = a 1 OR a 0 a 1 f(a 0) f(a 1) b 1 b 2 b 3 B

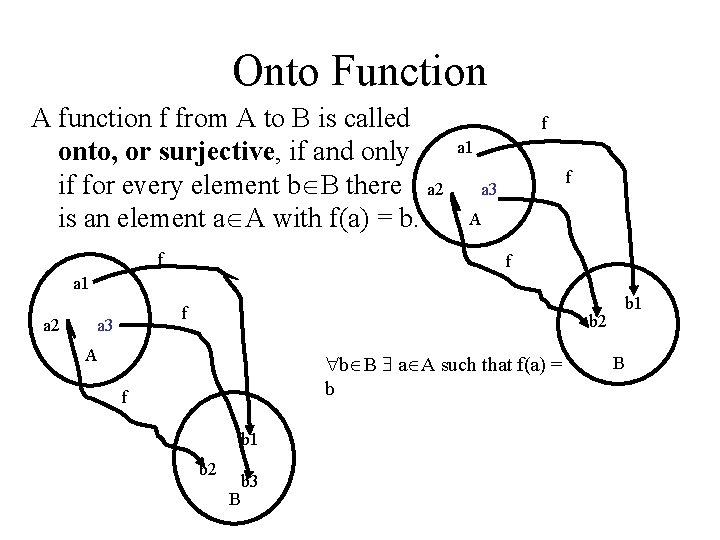
Onto Function A function f from A to B is called onto, or surjective, if and only if for every element b B there a 2 is an element a A with f(a) = b. f f a 1 f a 3 A f a 1 a 2 f a 3 b 1 b 2 A b B a A such that f(a) = b f b 1 b 2 B b 3 B

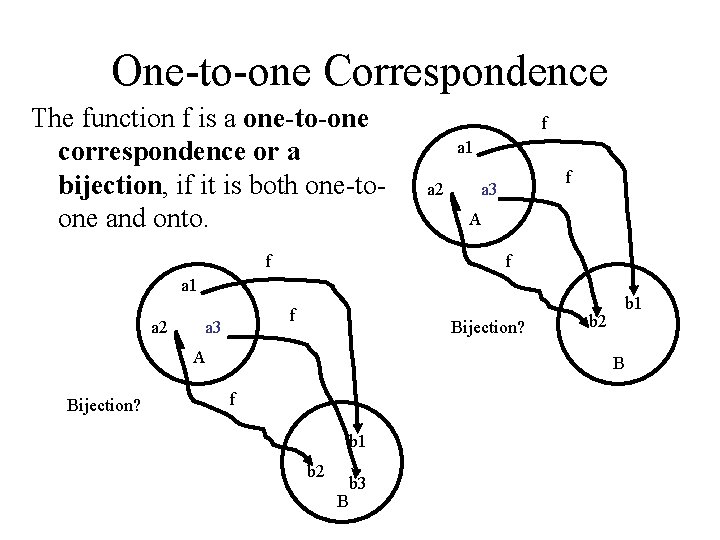
One-to-one Correspondence The function f is a one-to-one correspondence or a bijection, if it is both one-toone and onto. f f a 1 a 2 f a 3 A f a 1 a 2 f a 3 Bijection? A Bijection? b 1 b 2 B f b 1 b 2 B b 3

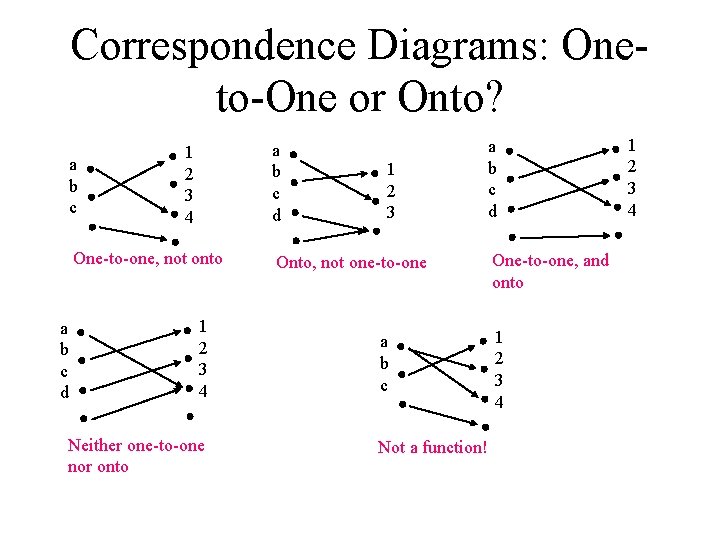
Correspondence Diagrams: Oneto-One or Onto? a b c d 1 2 3 4 One-to-one, not onto a b c d 1 2 3 4 Neither one-to-one nor onto 1 2 3 Onto, not one-to-one a b c Not a function! a b c d One-to-one, and onto 1 2 3 4

Inverse Function, f-1 Let f be a one-to-one correspondence from the set A to the set B. The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that if f(a) = b, then f-1(b) = a. Example: f b a f(a) = 3(a-1) f-1(b) = (b/3)+1 f-1

Examples Is each of the following (on the real numbers): a function? one-to-one? Onto? Invertible? f(x) = 1/x not a function f(0) undefined f(x) = x not a function since not defined for x<0 f(x) = x 2 is a function, not 1 -to-1 (-2, 2 both go to 4), not onto since no way to get to the negative numbers, not invertible

Sequence • A sequence is a discrete structure used to represent an ordered list. • A sequence is a function from a subset of the set of integers (usually either the set {0, 1, 2, . . . } or {1, 2, 3, . . . }to a set S. • We use the notation an to denote the image of the integer n. We call an a term of the sequence. • Notation to represent sequence is {an}

Examples • {1, 1/2, 1/3, 1/4, . . . } or the sequence {an} where an = 1/n, n Z+. • {1, 2, 4, 8, 16, . . . } = {an} where an = 2 n, n N. • {12, 22, 32, 42, . . . } = {an} where an = n 2, n Z+

Summations • Notation for describing the sum of the terms am+1, . . . , an from the sequence, {an} a m, n am+am+1+. . . + an = aj j=m • j is the index of summation (dummy variable) • The index of summation runs through all integers from its lower limit, m, to its upper limit, n.

Summations follow all the rules of multiplication and addition! c(1+2+…+n) = c + 2 c +…+ nc

Telescoping Sums Example

Closed Form Solutions A simple formula that can be used to calculate a sum without doing all the additions. Example: Proof: First we note that k 2 - (k-1)2 = k 2 - (k 2 -2 k+1) = 2 k-1. Since k 2 -(k-1)2 = 2 k-1, then we can sum each side from k=1 to k=n

Proof (cont. )

Big-O Notation • Let f and g be functions from the set of integers or the set of real numbers to the set of real numbers. We say that f(x) is O(g(x)) if there are constants C N and k R such that |f(x)| C|g(x)| whenever x > k. • We say “f(x) is big-oh of g(x)”. • The intuitive meaning is that as x gets large, the values of f(x) are no larger than a constant time the values of g(x), or f(x) is growing no faster than g(x). • The supposition is that x gets large, it will approach a simplified limit.

Show that 3 2 3 x +2 x +7 x+9 is O(x 3) Proof: We must show that constants C N and k R such that |3 x 3+2 x 2+7 x+9| C|x 3| whenever x > k. Choose k = 1 then 3 x 3+2 x 2+7 x+9 3 x 3+2 x 3+7 x 3+9 x 3 = 21 x 3 So let C = 21. Then 3 x 3+2 x 2+7 x+9 21 x 3 when x 1.

Show that n! is O(nn) Proof: We must show that constants C N and k R such that |n!| C|nn| whenever n > k. n! = n(n-1)(n-2)(n-3)…(3)(2)(1) n(n)(n)(n)…(n)(n)(n) n times =nn So choose k = 0 and C = 1

General Rules • Multiplication by a constant does not change the rate of growth. If f(n) = kg(n) where k is a constant, then f is O(g) and g is O(f). • The above means that there an infinite number of pairs C, k that satisfy the Big-O definition. • Addition of smaller terms does not change the rate of growth. If f(n) = g(n) + smaller order terms, then f is O(g) and g is O(f). Ex. : f(n) = 4 n 6 + 3 n 5 + 100 n 2 + 2 is O(n 6).

General Rules (cont. ) • If f 1(x) is O(g 1(x)) and f 2(x) is O(g 2(x)), then f 1(x)f 2(x) is O(g 1(x)g 2(x)). • Examples: 10 xlog 2 x is O(xlog 2 x) n!6 n 3 is O(n!n 3) =O(nn+3)

Example: Big-Oh Not Symmetric • Order matters in big-oh. Sometimes f is O(g) and g is O(f), but in general big-oh is not symmetric. Consider f(n) = 4 n and g(n) = n 2. f is O(g). • Can we prove that g is O(f)? Formally, constants C N and k R such that |n 2| C|4 n| whenever n > k? • No. To show this, we must prove that negation is true for all C and k. C N, k R, n>k such that n 2 > C|4 n|.

C N, k R, n>k such that n 2 > 4 n. C. • To prove that negation is true, start with arbitrary C and k. Must show/construct an n>k such that n 2 > 4 n. C • Easy to satisfy n > k, then • To satisfy n 2>4 n. C, divide both sides by n to get n>4 C. Pick n = max(4 C+1, k+1), which proves the negation.