Propositional Equivalences CSAPMA 202 Spring 2005 Rosen section

Propositional Equivalences CS/APMA 202, Spring 2005 Rosen, section 1. 2 Aaron Bloomfield 1

Tautology and Contradiction A tautology is a statement that is always true n p ¬p will always be true (Negation Law) A contradiction is a statement that is always false n p ¬p will always be false p T F p ¬p T T (Negation Law) p ¬p F F 2

Logical Equivalence A logical equivalence means that the two sides always have the same truth values n Symbol is ≡ or (we’ll use ≡) 3

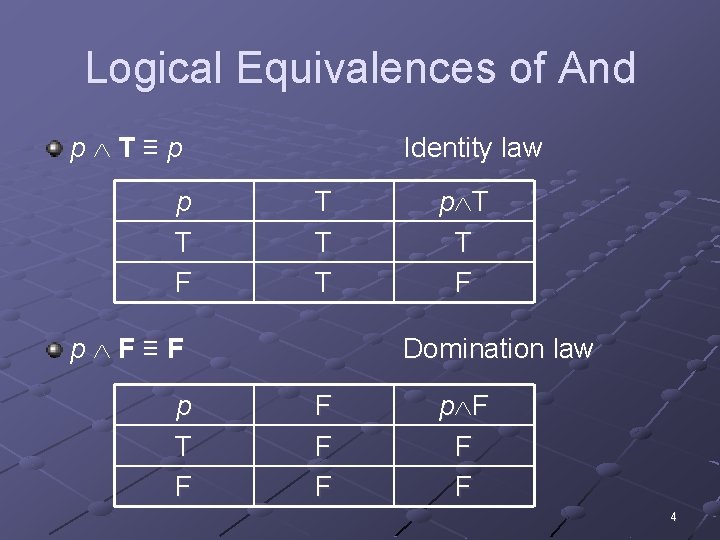
Logical Equivalences of And p T≡p p T F Identity law T T T p F≡F p T T F Domination law F F F p F F F 4

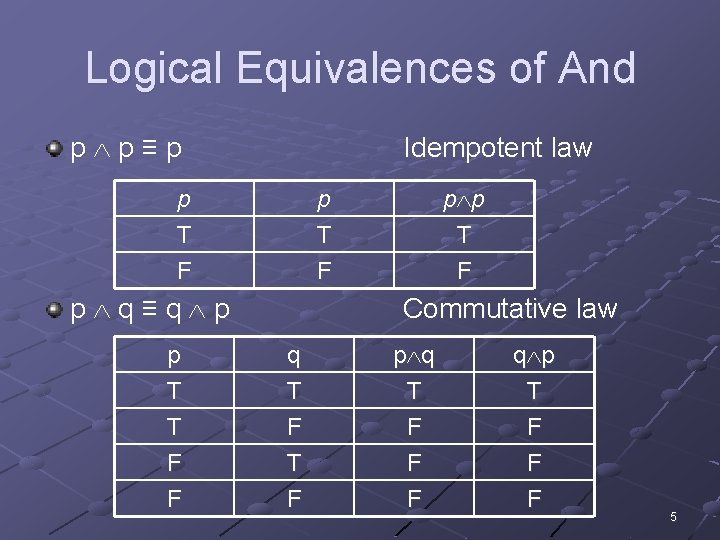
Logical Equivalences of And p p≡p Idempotent law p T F p q≡q p Commutative law p T T F q T F T p q T F F q p T F F F 5

Logical Equivalences of And (p q) r ≡ p (q r) Associative law p q (p q) r q r p (q r) T T T T T F T F F F F T T F F F F F F p q r 6

Logical Equivalences of Or p T≡T p F≡p p p≡p p q≡q p (p q) r ≡ p (q r) Identity law Domination law Idempotent law Commutative law Associative law 7

Corollary of the Associative Law (p q) r ≡ p q r Similar to (3+4)+5 = 3+4+5 Only works if ALL the operators are the same! 8

Logical Equivalences of Not ¬(¬p) ≡ p p ¬p ≡ T p ¬p ≡ F Double negation law Negation law 9

Sidewalk chalk guy n Source: http: //www. gprime. net/images/sidewalkchalkguy/ 10

De. Morgan’s Law Probably the most important logical equivalence To negate p q (or p q), you “flip” the sign, and negate BOTH p and q n n Thus, ¬(p q) ≡ ¬p ¬q p q p q (p q) p q TT F F T F T T T F F FT T F F T T T F F FF T T 11

Yet more equivalences Distributive: p (q r) ≡ (p q) (p r) Absorption p (p q) ≡ p 12

How to prove two propositions are equivalent? Two methods: n Using truth tables Not good for long formula In this course, only allowed if specifically stated! n Using the logical equivalences The preferred method Example: Rosen question 23, page 27 n Show that: 13

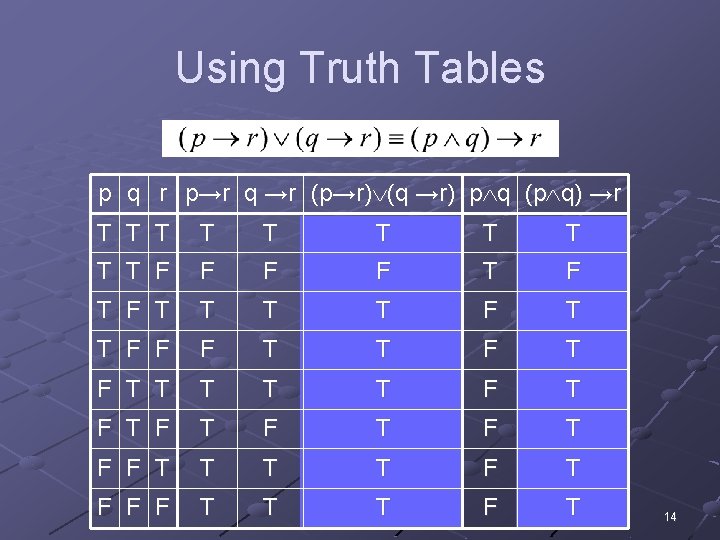
Using Truth Tables p q r p→r q →r (p→r) (q →r) p q (p q) →r T T T T T F F T F T T F F F T T T F T F T F F T T F T F F F T T T F T 14

Using Logical Equivalences Original statement Definition of implication De. Morgan’s Law Associativity of Or Re-arranging Idempotent Law 15

Quick survey n a) b) c) d) I understood the logical equivalences on the last slide Very well Okay Not really Not at all 16

Logical Thinking At a trial: n n n Bill says: “Sue is guilty and Fred is innocent. ” Sue says: “If Bill is guilty, then so is Fred. ” Fred says: “I am innocent, but at least one of the others is guilty. ” Let b = Bill is innocent, f = Fred is innocent, and s = Sue is innocent Statements are: n n n ¬s f ¬b → ¬f f (¬b ¬s) 18

Can all of their statements be true? Show: (¬s f) (¬b → ¬f) (f (¬b ¬s)) b f s ¬b ¬f ¬s ¬s f ¬b→¬f ¬b ¬s f (¬b ¬s) T T T F F T T F F F T T T F T F F F T T T F F T T F T F T T F F T T T F 19

Are all of their statements true? Show values for s, b, and f such that the equation is true Original statement Definition of implication Associativity of AND Re-arranging Idempotent law Re-arranging Absorption law Re-arranging Distributive law Negation law Domination law Associativity of AND 20

What if it weren’t possible to assign such values to s, b, and f? Original statement Definition of implication. . . (same as previous slide) Domination law Re-arranging Negation law Domination law Contradiction! 21

Quick survey n a) b) c) d) I feel I can prove a logical equivalence myself Absolutely With a bit more practice Not really Not at all 22

Logic Puzzles Rosen, page 20, questions 51 -55 Knights always tell the truth, knaves always lie A says “At least one of us is a knave” and B says nothing A says “The two of us are both knights” and B says “A is a knave” A says “I am a knave or B is a knight” and B says nothing Both A and B say “I am a knight” A says “We are both knaves” and B says nothing 23

Sand Castles 24

Functional completeness is discussed on page 27 (questions 37 -39) of the text All the “extended” operators have equivalences using only the 3 basic operators (and, or, not) n The extended operators: nand, nor, xor, conditional, bi -conditional Given a limited set of operators, can you write an equivalence of the 3 basic operators? n If so, then that group of operators is functionally complete 25

Rosen, § 1. 2 question 46 Show that | (NAND) is functionally complete Equivalence of NOT: n n n p | p ≡ p (p p ) ≡ p (p ) ≡ p Equivalence of NAND Idempotent law 26

Rosen, § 1. 2 question 46 Equivalence of AND: n n n p q ≡ (p | q ) p|p (p | q ) | ( p | q ) Definition of nand How to do a not using nands Negation of (p | q) Equivalence of OR: n n p q ≡ ( p q ) De. Morgan’s equivalence of OR As we can do AND and OR with NANDs, we can thus do ORs with NANDs Thus, NAND is functionally complete 27

Quick survey n a) b) c) d) I felt I understood the material in this slide set… Very well With some review, I’ll be good Not really Not at all 28

Quick survey n a) b) c) d) The pace of the lecture for this slide set was… Fast About right A little slow Too slow 29