Logical Form and Logical Equivalence Lecture 1 Section

Logical Form and Logical Equivalence Lecture 1 Section 1. 1 Thu, Jan 19, 2006

Statements A statement is a sentence that is either true or false, but not both. ¢ These are statements: ¢ It is raining. l I am carrying an umbrella. l ¢ These are not statements: Hello. l Are you there? l Go away! l

Logical Operators ¢ Binary operators l l ¢ Unary operator l ¢ Conjunction – “and”. Disjunction – “or”. Negation – “not”. Other operators l l l XOR – “exclusive or” NAND – “not both” NOR – “neither”

Logical Symbols Statements are represented by letters: p, q, r, etc. ¢ means “and”. ¢ means “or”. ¢ means “not”. ¢

Examples ¢ Basic statements l l ¢ p = “It is raining. ” q = “I am carrying an umbrella. ” Compound statements l l l p q = “It is raining and I am carrying an umbrella. ” p q = “ It is raining or I am carrying an umbrella. ” p = “It is not raining. ”

False Negations ¢ Statement l ¢ False negation l ¢ Everyone likes me. Everyone does not like me. True negation l Someone does not like me.

False Negations ¢ Statement l ¢ False negation l ¢ Someone likes me. Someone does not like me. True negation l No one likes me.

Truth Table of an Expression Make a column for every variable. ¢ List every possible combination of truth values of the variables. ¢ Make one more column for the expression. ¢ Write the truth value of the expression for each combination of truth values of the variables. ¢

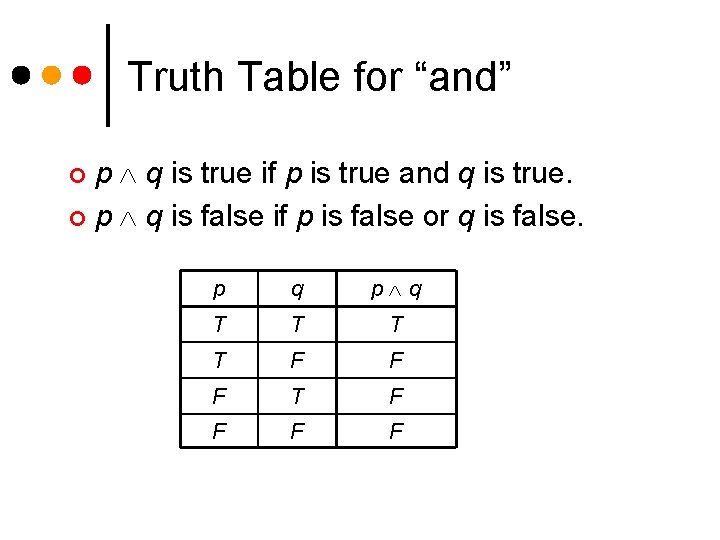
Truth Table for “and” p q is true if p is true and q is true. ¢ p q is false if p is false or q is false. ¢ p q T T F F F T F F

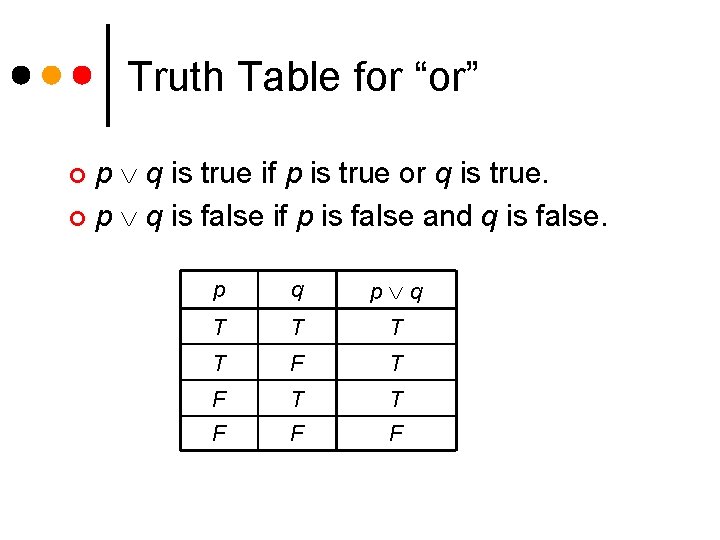
Truth Table for “or” p q is true if p is true or q is true. ¢ p q is false if p is false and q is false. ¢ p q T T F F F

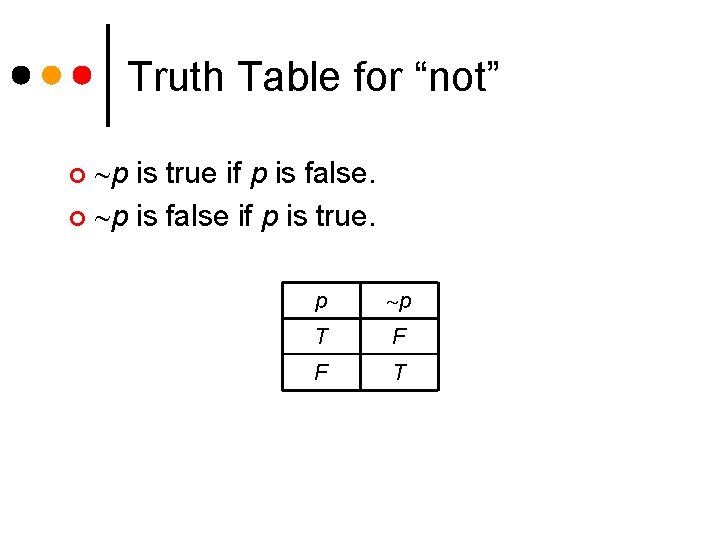
Truth Table for “not” p is true if p is false. ¢ p is false if p is true. ¢ p p T F F T

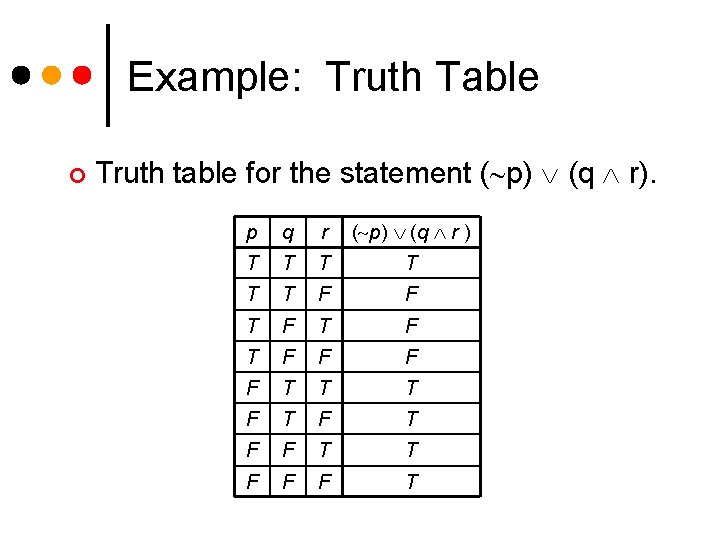
Example: Truth Table ¢ Truth table for the statement ( p) (q r). p q r ( p) (q r ) T T T F F T F T F F T T F F F T

Logical Equivalence ¢ Two statements are logically equivalent if they have the same truth values for all combinations of truth values of their variables.

Example: Logical Equivalence ¢ (p q) ( p q) p q (p q) ( p q) T T T F F F F T T

De. Morgan’s Laws: (p q) ( p) ( q) ¢ If it is not true that ¢ i < size && value != array[i] then it is true that i >= size || value == array[i] ¢ If it is not true that x 5 or x 10, then it is true that x > 5 and x < 10.

Tautologies and Contradictions ¢ ¢ ¢ A tautology is a statement that is logically equivalent to T. A contradiction is a statement that is logically equivalent to F. Some tautologies: l l ¢ p p p q ( p q) Some contradictions: l l p p p q ( p q)