Proofs Using Logical Equivalences Rosen 1 2 List

Proofs Using Logical Equivalences Rosen 1. 2

List of Logical Equivalences p T p; p F p Identity Laws p T T; p F F Domination Laws p p p; p p p Idempotent Laws ( p) p Double Negation Law p q q p; p q q p Commutative Laws (p q) r p (q r); (p q) r p (q r) Associative Laws

List of Equivalences p (q r) (p q) (p r) Distribution Laws (p q) ( p q) De Morgan’s Laws p p T p p F (p q) ( p q) Miscellaneous Or Tautology And Contradiction Implication Equivalence p q (p q) (q p) Biconditional Equivalence

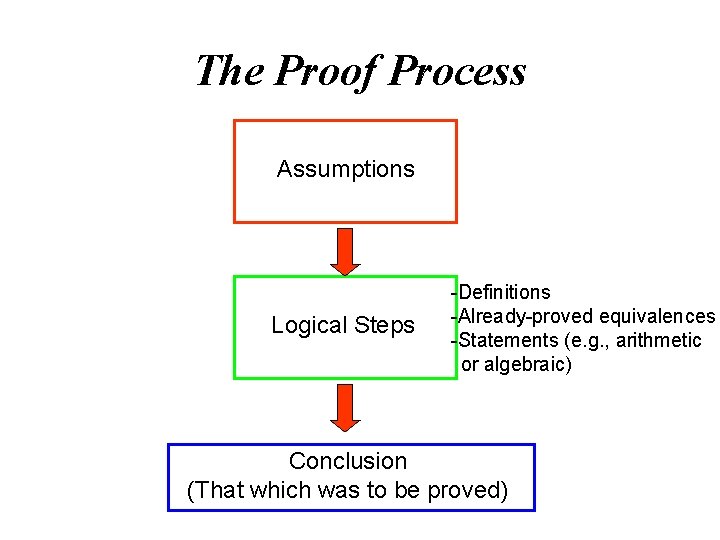
The Proof Process Assumptions Logical Steps -Definitions -Already-proved equivalences -Statements (e. g. , arithmetic or algebraic) Conclusion (That which was to be proved)

Prove: (p q) q p q (p q) q q (p q) (q p) (q q) (q p) T q p p q Left-Hand Statement Commutative Distributive Or Tautology Identity Commutative Begin with exactly the left-hand side statement End with exactly what is on the right Justify EVERY step with a logical equivalence

Prove: (p q) q p q (p q) q Left-Hand Statement q (p q) Commutative (q p) (q q) Distributive Why did we need this step? Our logical equivalence specified that is distributive on the right. This does not guarantee the equivalence works on the left! Ex. : Matrix multiplication is not always commutative (Note that whether or not is distributive on the left is not the point here. )

Prove: p q q p p q p q q p ( q) p q p Contrapositive Implication Equivalence Commutative Double Negation Implication Equivalence

Prove: p p q is a tautology Must show that the statement is true for any value of p, q. p p q p (p q) Implication Equivalence ( p p) q Associative (p p) q Commutative T q Or Tautology q T Commutative T Domination This tautology is called the addition rule of inference.

Why do I have to justify everything? • Note that your operation must have the same order of operands as the rule you quote unless you have already proven (and cite the proof) that order is not important. • 3+4 = 4+3 • 3/4 4/3 • A*B B*A for everything (for example, matrix multiplication)

Prove: (p q) p is a tautology (p q) p ( q p) p q ( p p) q (p p) q T T Implication Equivalence De. Morgan’s Commutative Associative Commutative Or Tautology Domination

Prove or Disprove p q ? ? ? To prove that something is not true it is enough to provide one counter-example. (Something that is true must be true in every case. ) p q p q FT T F The statements are not logically equivalent

Prove: p q ( p q) (q p) ( p q) ( q p) (p q) p q Biconditional Equivalence Implication Equivalence (x 2) Double Negation Commutative Double Negation Implication Equivalence (x 2) Biconditional Equivalence