Extremes in a Varied Climate Chris Ferro Climate














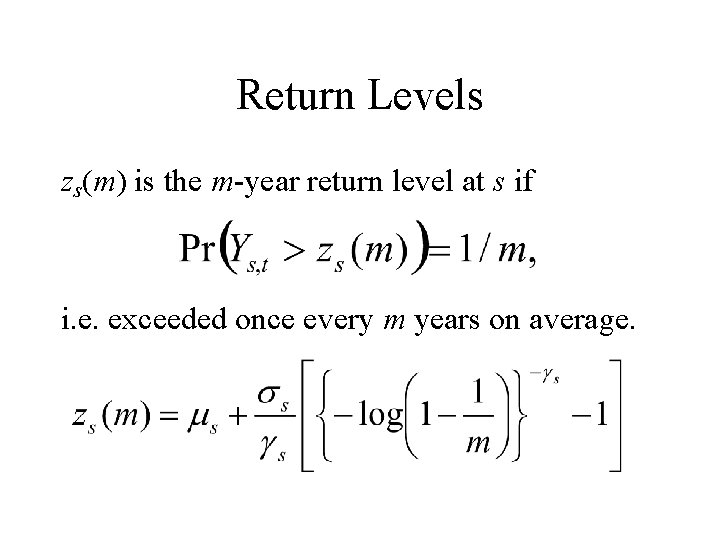








- Slides: 35

Extremes in a Varied Climate Chris Ferro Climate Analysis Group Department of Meteorology University of Reading 1. Significance of distributional changes 2. Extreme-value analysis of gridded data

Significance of Changes Compare daily data at single grid point in Assume X 1, …, Xn have same distribution Assume Y 1, …, Yn have same distribution

Quantiles xp is the p-quantile of the control if An estimate of xp is where are the order statistics.

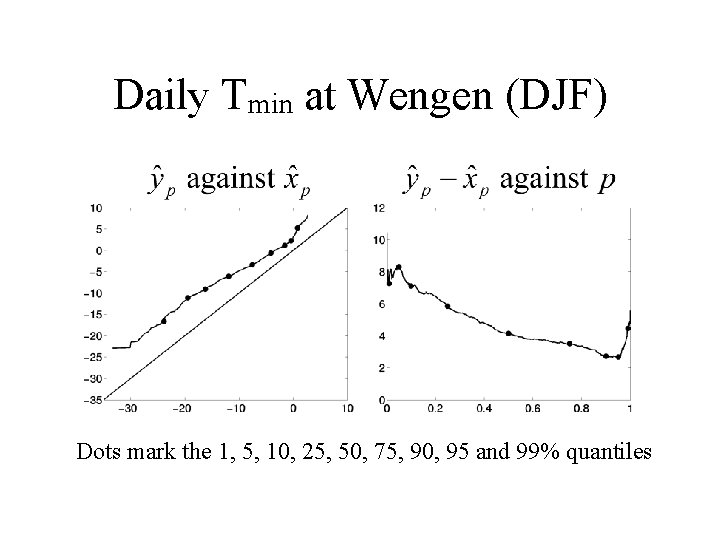
Daily Tmin at Wengen (DJF) Dots mark the 1, 5, 10, 25, 50, 75, 90, 95 and 99% quantiles

Confidence Intervals Quantify the uncertainty due to finite samples. A (1 – α)-confidence interval for is (Lp, Up) if

Resampling Replicating the experiment would reveal sampling variation of the estimate. Mimic replication by resampling from data. Must preserve any dependence – time (e. g. pre-whitening, blocking) – space (e. g. pairing)

Bootstrapping 1 For b = 1, …, B (large) resample {X 1*, …, Xn*} and {Y 1*, …, Yn*} compute Then

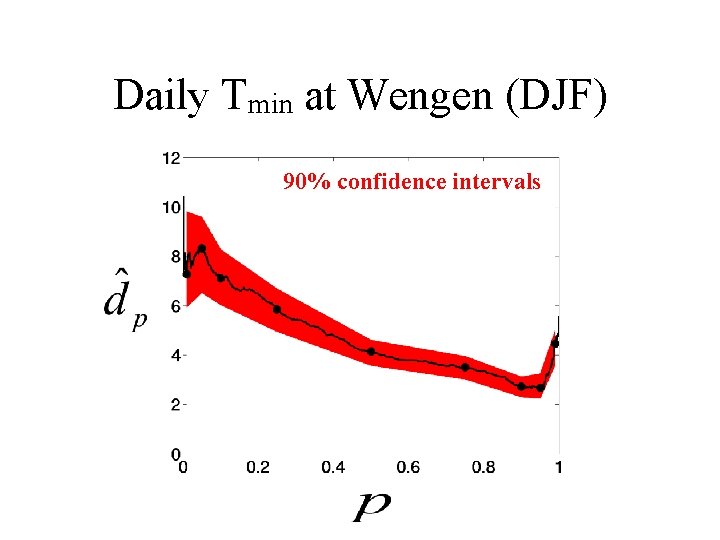
Daily Tmin at Wengen (DJF) 90% confidence intervals

Descriptive Hypotheses 1. No change: Y X dp = 0 for all p reject unless 2. Location change: Y X + m for some m dp = m for some m and all p reject unless 3. Location-scale change: Y s. X + m 4. Scale change (if natural origin): Y s. X

Simultaneous Intervals Simultaneous (1 – α)-confidence intervals for dp 1, …, dpm are (Lp 1, Up 1), …, (Lpm, Upm) if Wider than pointwise intervals, e. g.

Bootstrapping 2 For each p bootstrap set with k chosen to give correct confidence level: estimate level by proportion of the B sets with at least one point outside the intervals.

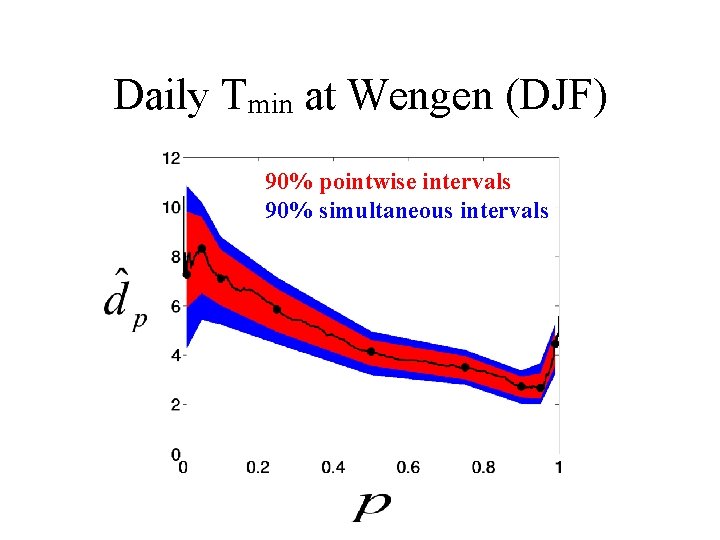
Daily Tmin at Wengen (DJF) 90% pointwise intervals 90% simultaneous intervals

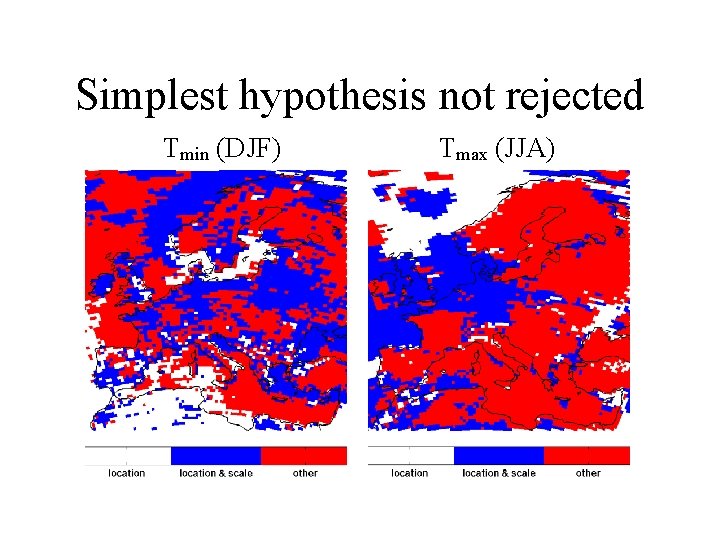
Simplest hypothesis not rejected Tmin (DJF) Tmax (JJA)

Other issues • Interpretation tricky when distributions change within samples: adjust for trends • Bootstrapping quantiles is difficult: more sophisticated bootstrap methods • Field significance • Computational cost

Conclusions • Quantiles describe entire distribution • Confidence intervals quantify uncertainty • Bootstrapping can account for dependence

Extreme-value Analysis • Summarise extremes at each grid point • Estimate return levels and other quantities • Framework for quantifying uncertainty • Summarise model output • Validate and compare models • Downscale model output

Annual Maxima Let Ys, t be the largest daily precipitation value at grid point s in year t. s = 1, …, 11766 grid points t = 1, …, 31 years Assume Ys, 1, …, Ys, 31 are independent and have the same distribution.

GEV Distribution Probability theory suggests the generalised extreme-value distribution for annual maxima: with parameters
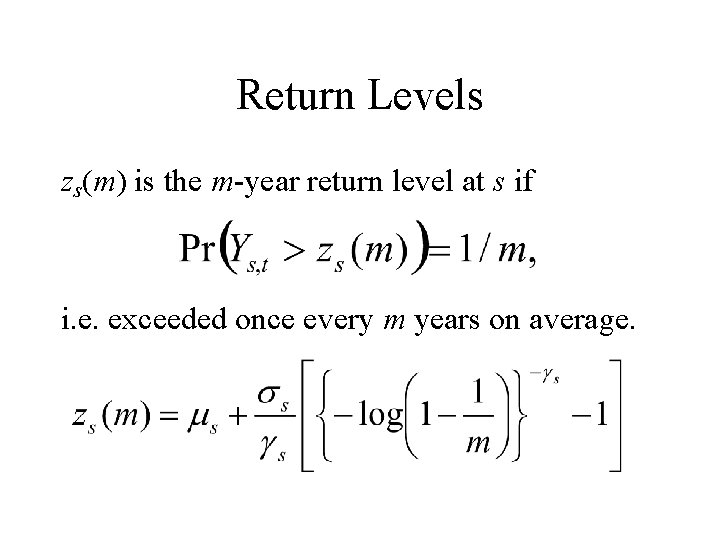
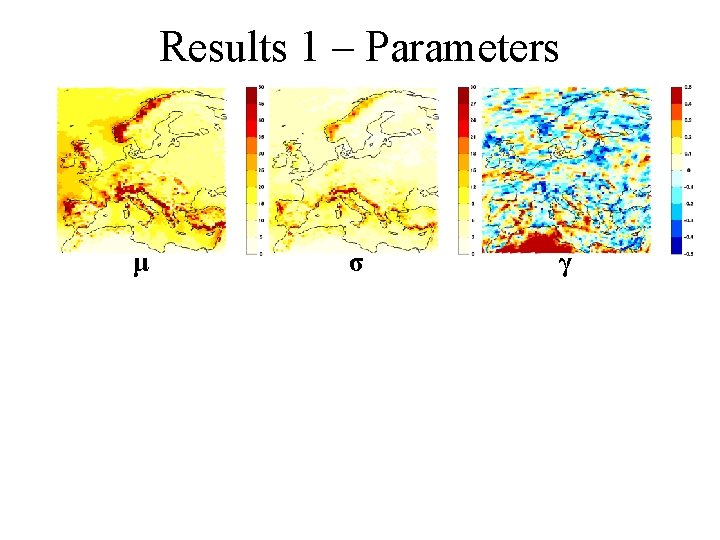
Return Levels zs(m) is the m-year return level at s if i. e. exceeded once every m years on average.

Fitting the GEV Find to maximise likelihood: Estimate has variance is obtained from

Results 1 – Parameters μ σ γ

Results 1 – Return Levels z(100) % standard error

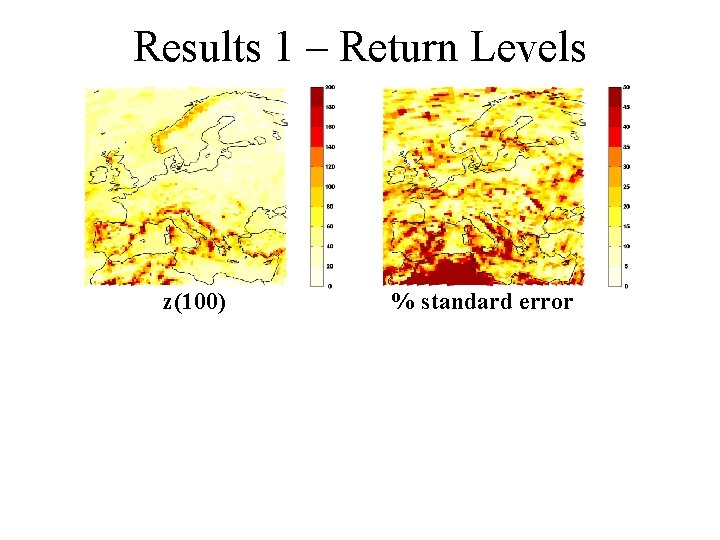
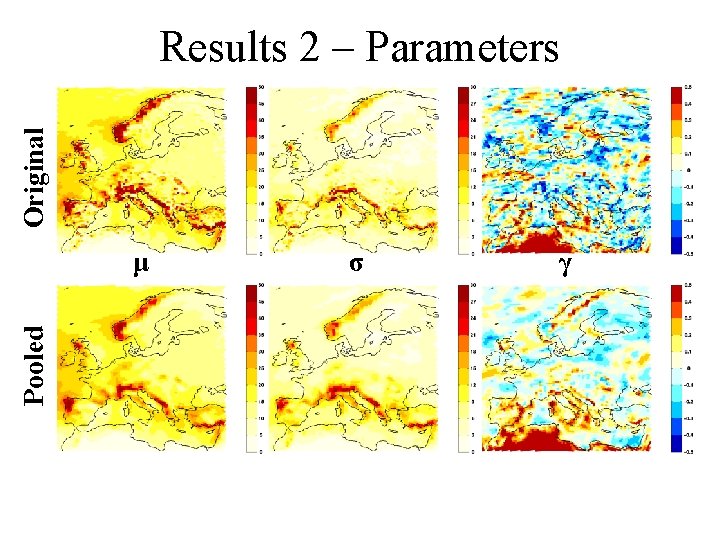
Pooling Grid Points Often if r is close to s. Assume if r is a neighbour (r ~ s). Maximise Using 9 × 31 observations increases precision.

Standard Errors Taylor expansion yields Independence of grid points implies H = V, leaving For dependence, estimate V using variance of

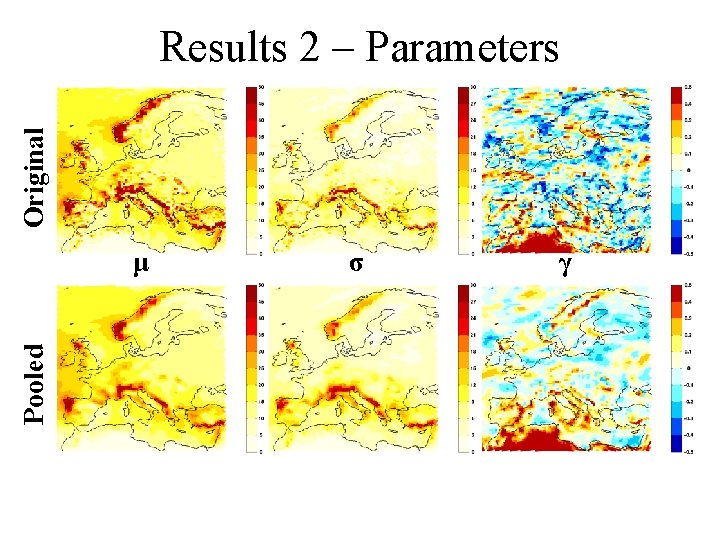
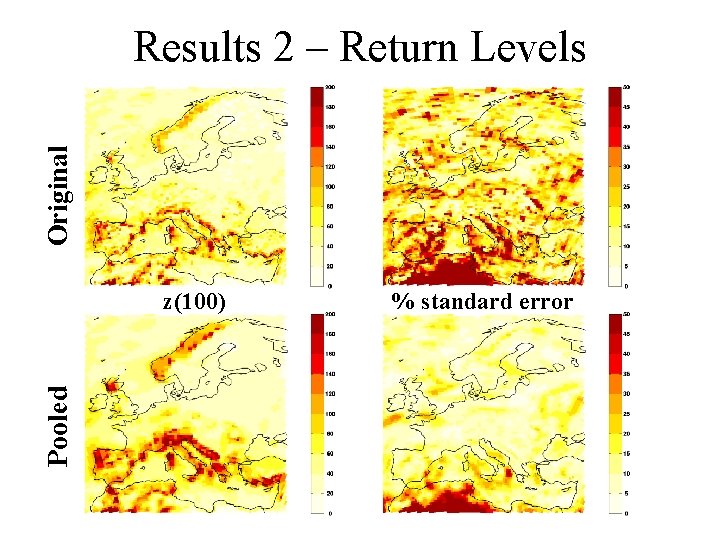
Original Results 2 – Parameters Pooled μ σ γ

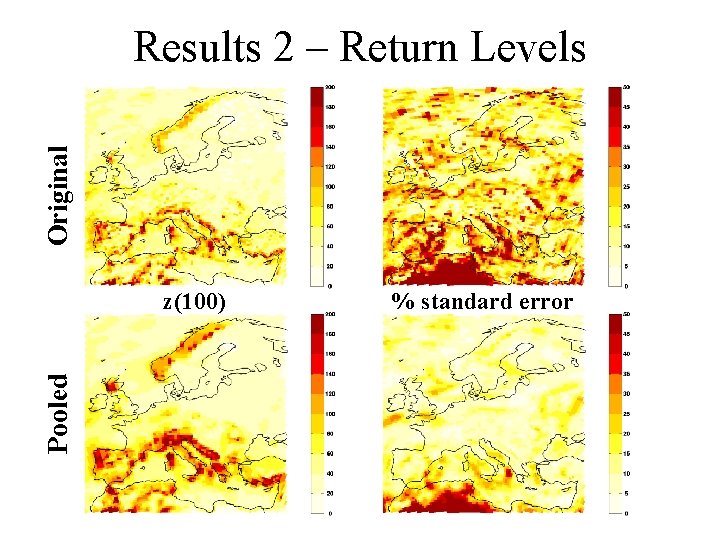
Original Results 2 – Return Levels Pooled z(100) % standard error

Local Variations Potential bias if for r ~ s. Reduce bias by modelling, e. g. Should exploit physical knowledge.

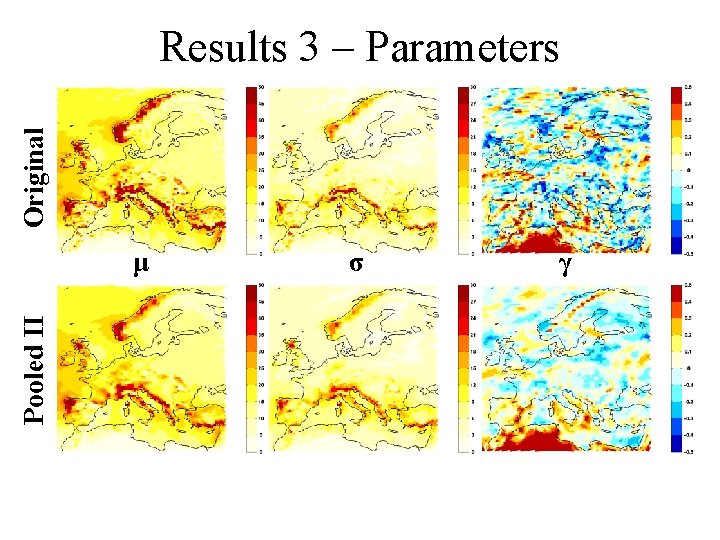
Original Results 3 – Parameters Pooled II μ σ γ

Original Results 2 – Parameters Pooled μ σ γ

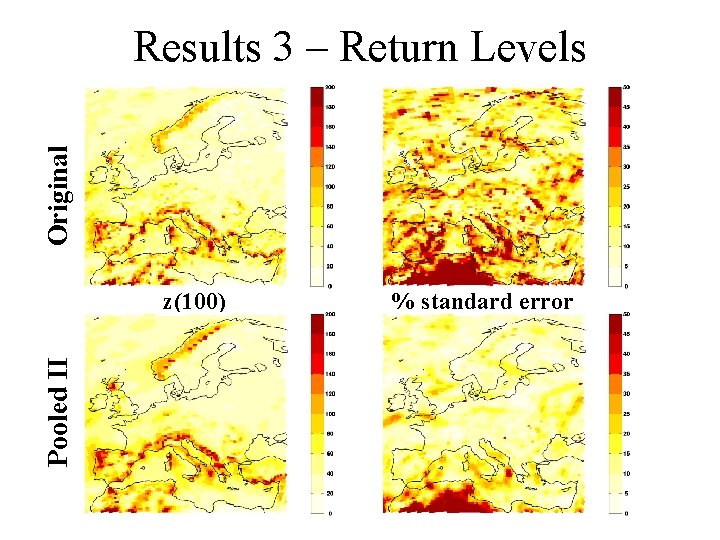
Original Results 3 – Return Levels Pooled II z(100) % standard error

Original Results 2 – Return Levels Pooled z(100) % standard error

Conclusions • Pooling can clarify extremal behaviour increase precision introduce bias • Careful modelling can reduce bias

Future Directions • • Diagnostics for adequacy of GEV model Threshold exceedances; k-largest maxima Size and shape of neighbourhoods Less weight on more distant grid points More accurate standard error estimates Model any changes through time Clustering of extremes in space and time

References • Davison & Hinkley (1997) Bootstrap Methods and their Application. Cambridge University Press. • Davison & Ramesh (2000) Local likelihood smoothing of sample extremes. J. Royal Statistical Soc. B, 62, 191– 208. • Smith (1990) Regional estimation from spatially dependent data. www. unc. edu/depts/statistics/faculty/rsmith. html • Wilks (1997) Resampling hypothesis tests for autocorrelated fields. J. Climate, 10, 65 – 82. c. a. t. ferro@reading. ac. uk www. met. rdg. ac. uk/~sws 02 caf

Commentary Annual maximum at grid point s is GEV. 1. Estimate using data at s. 2. Estimate using data in neighbourhood of s. Bias can occur if 3. Allow for local variation in parameters.
 Varied climate
Varied climate Extremes of a proportion
Extremes of a proportion Box and whisker plots worksheet
Box and whisker plots worksheet Avoid extremes
Avoid extremes Means and extremes of proportions
Means and extremes of proportions Means extremes ratio theorem
Means extremes ratio theorem Equal ratio theorem
Equal ratio theorem Means and extremes examples
Means and extremes examples Means and extremes
Means and extremes Mental quality consisting of the ability to learn
Mental quality consisting of the ability to learn Bicultural couples tend to demonstrate extremes in
Bicultural couples tend to demonstrate extremes in Means and extremes
Means and extremes Means-extremes property of proportion
Means-extremes property of proportion Varied sentence starters
Varied sentence starters Outline vs contour lines
Outline vs contour lines Serving size examples
Serving size examples Process choice is driven
Process choice is driven Different sentence openers
Different sentence openers Varied expertise
Varied expertise Varying sentence structure
Varying sentence structure What does varied fluency mean
What does varied fluency mean Climate change 2014 mitigation of climate change
Climate change 2014 mitigation of climate change Una pallina di ferro da 30 g viene lasciata cadere
Una pallina di ferro da 30 g viene lasciata cadere Cubilot
Cubilot Ferro de passar
Ferro de passar Enrico ferro
Enrico ferro Ferro fundido
Ferro fundido Classificação do ferro fundido
Classificação do ferro fundido Omnibus ferro militis perterritis
Omnibus ferro militis perterritis Ferro fundido
Ferro fundido Calor latente de condensação
Calor latente de condensação Ossido di ferro marte
Ossido di ferro marte Ferro fundido
Ferro fundido Aço e ferro fundido
Aço e ferro fundido Ledeburite trasformata
Ledeburite trasformata Fei duas barras sendo uma de ferro e outra de aluminio
Fei duas barras sendo uma de ferro e outra de aluminio


























































