8 1 Ratio and Proportion Objective After studying

8. 1 Ratio and Proportion Objective: After studying this section, you will be able to recognize and work with ratios and proportions. You will be able to apply the product and ratio theorems and calculate geometric means.

Definition A ratio is a quotient of two numbers Ratios can be written in the following ways the ratio of 5 meters to 3 meters 5: 3 5 to 3 Unless otherwise specified, a ratio is given in lowest terms.

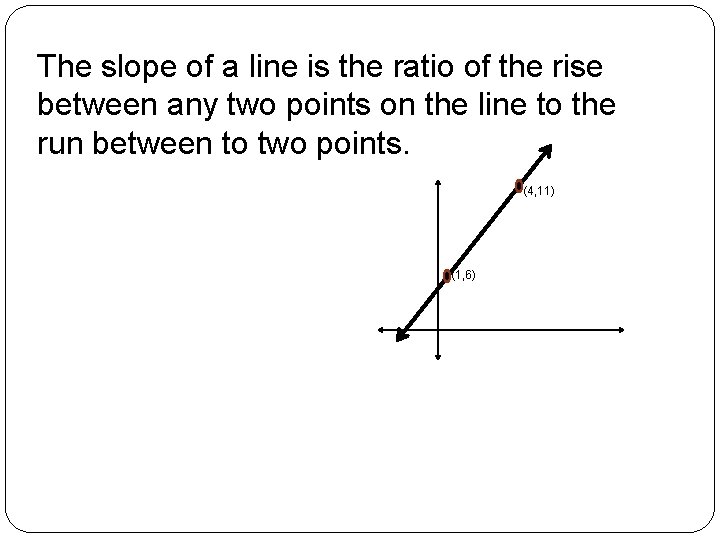
The slope of a line is the ratio of the rise between any two points on the line to the run between to two points. (4, 11) (1, 6)

Definition A proportion is an equation stating that two or more ratios are equal. 5: 15 = 15: 45 Most proportions will contain only two ratios and will be written in one of the following equivalent forms.

In both of these forms, a is called the first term b is called the second term c is called the third term d is called the fourth term The Product and Ratio Theorem In a proportion containing four terms. The first and fourth terms are called the extremes The second and third terms are called the means Theorem In a proportion, the product of the means is equal to the product of the extremes. (Means-Extremes Product Theorem)

Theorem If the product of a pair of nonzero numbers is equal to the product of another pair of nonzero numbers, then either pair of numbers may be made the extremes, and the other pair the means, of a proportion. (Means-Extremes Ratio Theorem)

What did that theorem say? ? pq = rs can be written as any of the following:

The Geometric Mean In a mean proportion, the means are the same. 4 is the geometric mean between 1 and 16 in the first example and r is the geometric mean between a and q in the second example. Definition If the means in a proportion are equal, either mean is called a geometric means, or mean proportional, between the extremes.

The Arithmetic Mean The arithmetic mean is the average between two numbers. Find the geometric and arithmetic means between 3 and 27

1. Solve for x 2. Find the fourth term (sometimes called the fourth proportional) of a proportion if the first three terms are 2, 3, and 4. 3. Find the mean proportional(s) between 4 and 16

4. If 3 x = 4 y, find the ratio of x to y. 5. 6.

Summary: Show that if then Homework: worksheet ,