Chapter 7 Proportions and Similarity 7 1 Proportions

Chapter 7: Proportions and Similarity

7. 1 - Proportions n Make a Frayer foldable 7. 1 Ratio and Proportion

Ratio n A comparison of two quantities using division n 3 ways to write a ratio: n a to b n n a: b

Proportion n An equation stating that two ratios are equal n Example: n Cross products: means and extremes n Example: a and d = extremes b and c = means ad = bc

n. There are 480 sophomores and 520 juniors in a high school. Find the ratio of juniors to sophomores.

Your Turn: solve these examples Ex:

Your Turn: solve this example n The ratios of the measures of three angles of a triangle are 5: 7: 8. Find the angle measures. A strip of wood molding that is 33 inches long is cut into two pieces whose lengths are in the ratio of 7: 4. What are the lengths of the two pieces?

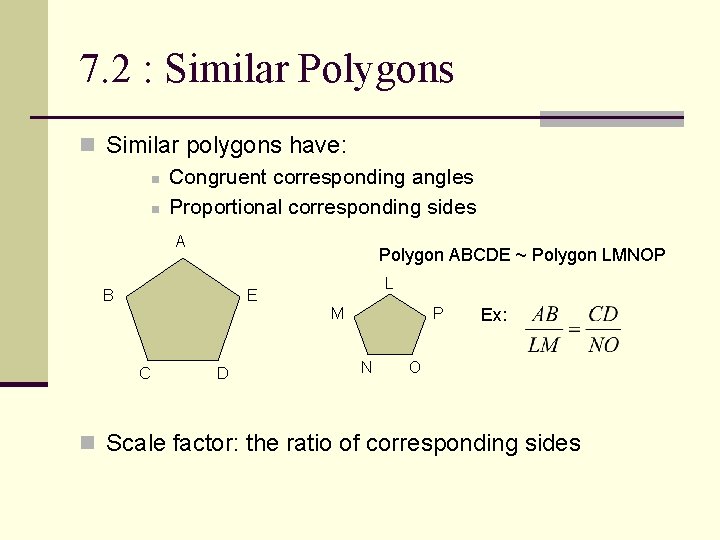
7. 2 : Similar Polygons n Similar polygons have: n Congruent corresponding angles n Proportional corresponding sides A Polygon ABCDE ~ Polygon LMNOP B L E M C D P N Ex: O n Scale factor: the ratio of corresponding sides

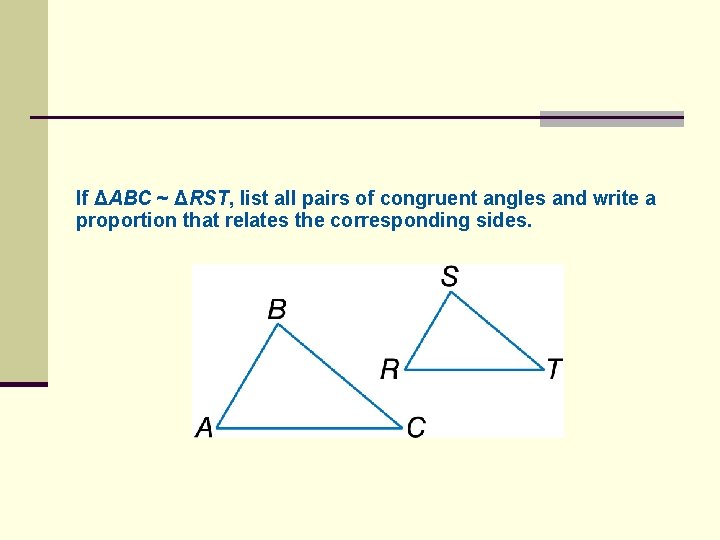
If ΔABC ~ ΔRST, list all pairs of congruent angles and write a proportion that relates the corresponding sides.

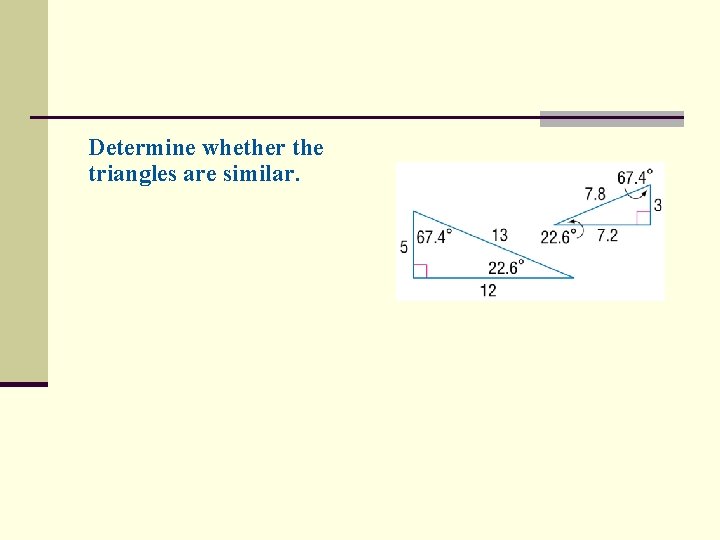
Determine whether the triangles are similar.

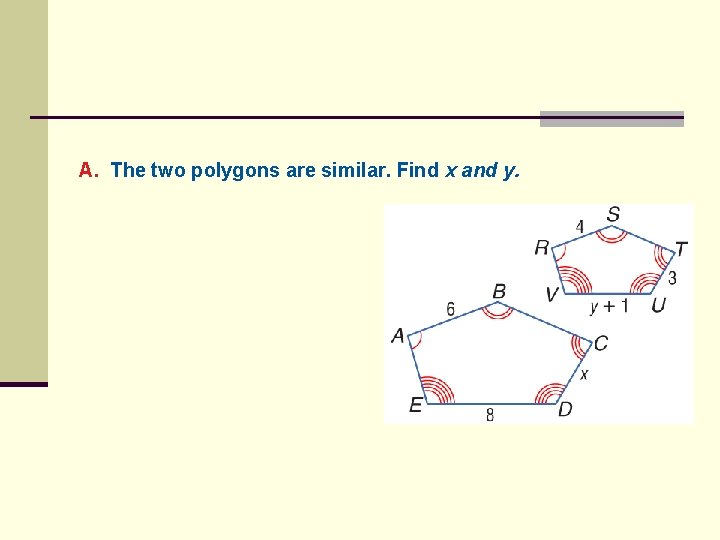
A. The two polygons are similar. Find x and y.

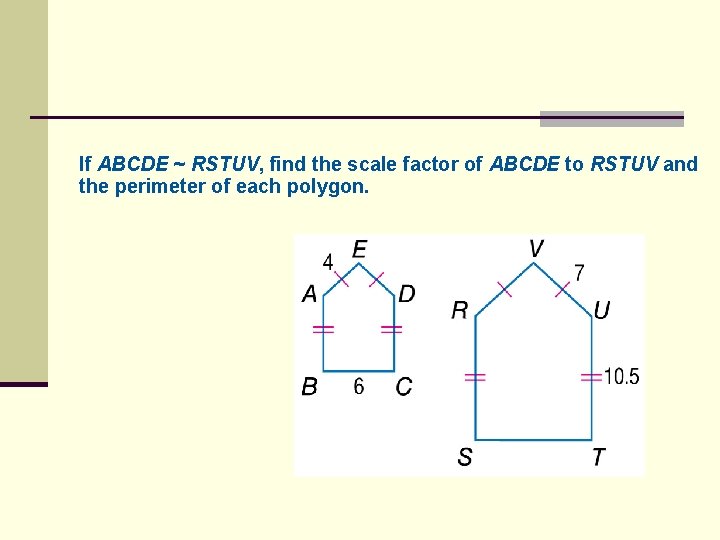
If ABCDE ~ RSTUV, find the scale factor of ABCDE to RSTUV and the perimeter of each polygon.

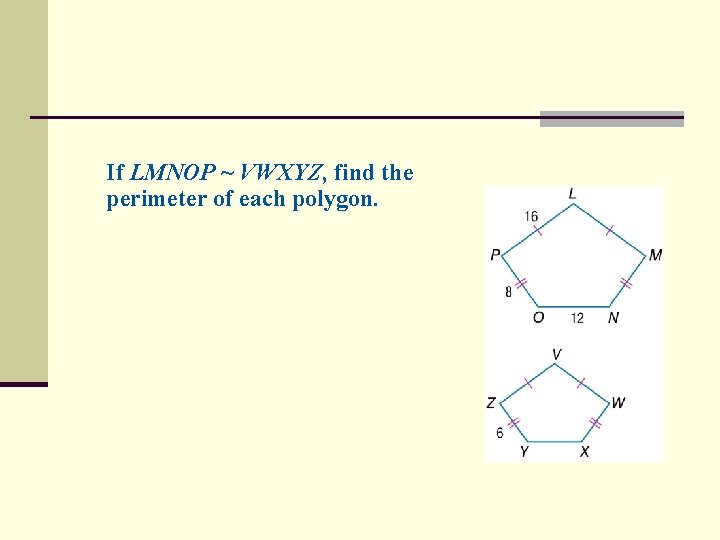
If LMNOP ~ VWXYZ, find the perimeter of each polygon.

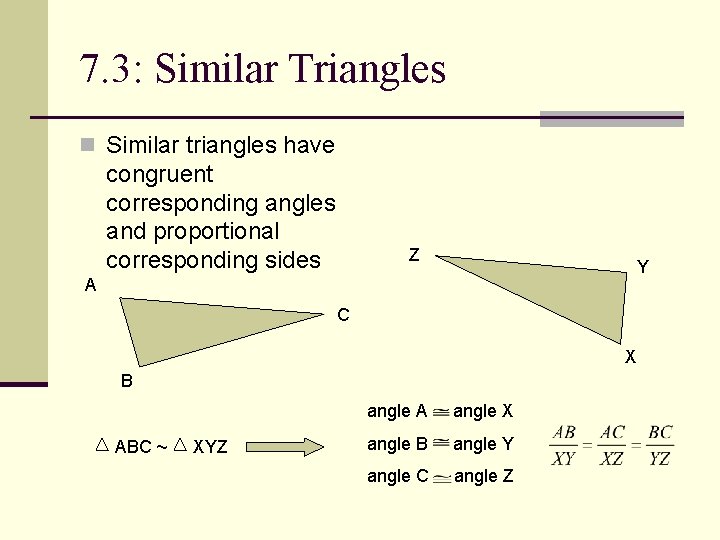
7. 3: Similar Triangles n Similar triangles have congruent corresponding angles and proportional corresponding sides Z Y A C X B ABC ~ XYZ angle A angle X angle B angle Y angle C angle Z

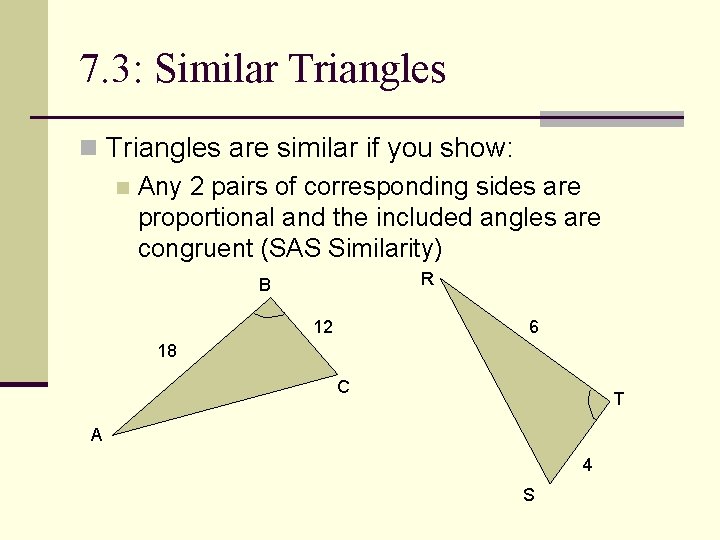
7. 3: Similar Triangles n Triangles are similar if you show: n Any 2 pairs of corresponding sides are proportional and the included angles are congruent (SAS Similarity) R B 12 6 18 C T A 4 S

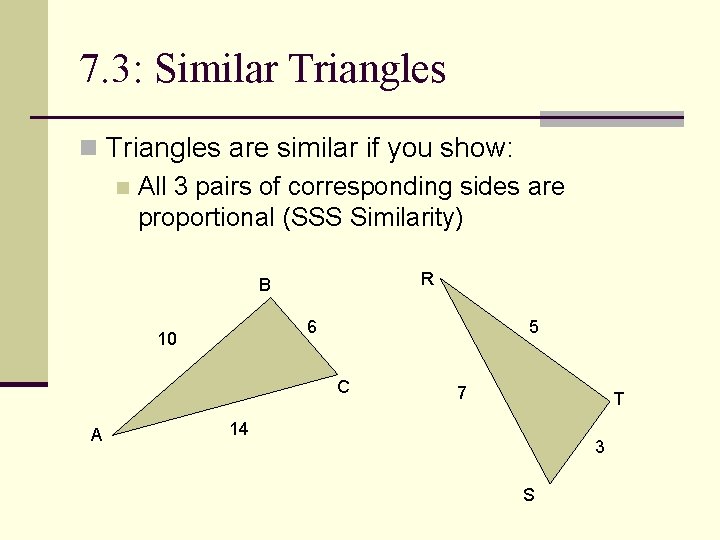
7. 3: Similar Triangles n Triangles are similar if you show: n All 3 pairs of corresponding sides are proportional (SSS Similarity) R B 6 10 5 C A 7 T 14 3 S

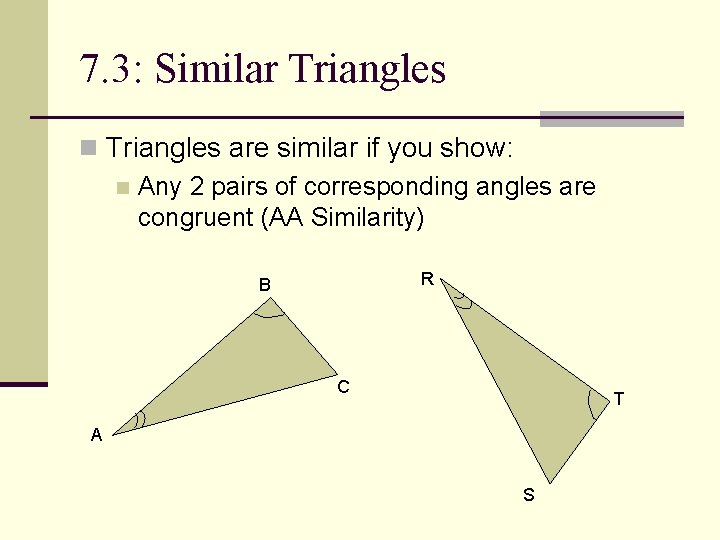
7. 3: Similar Triangles n Triangles are similar if you show: n Any 2 pairs of corresponding angles are congruent (AA Similarity) R B C T A S

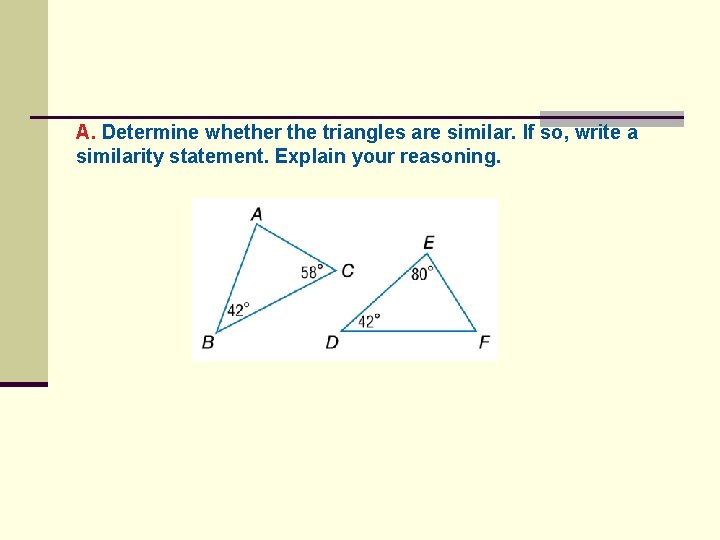
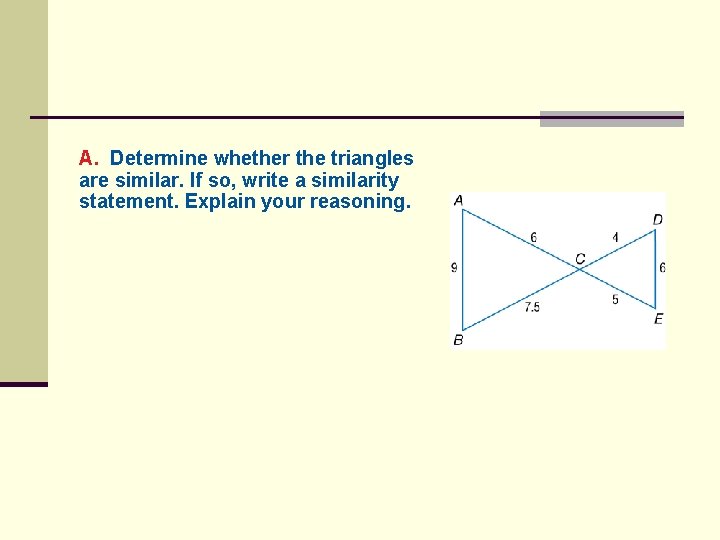
A. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

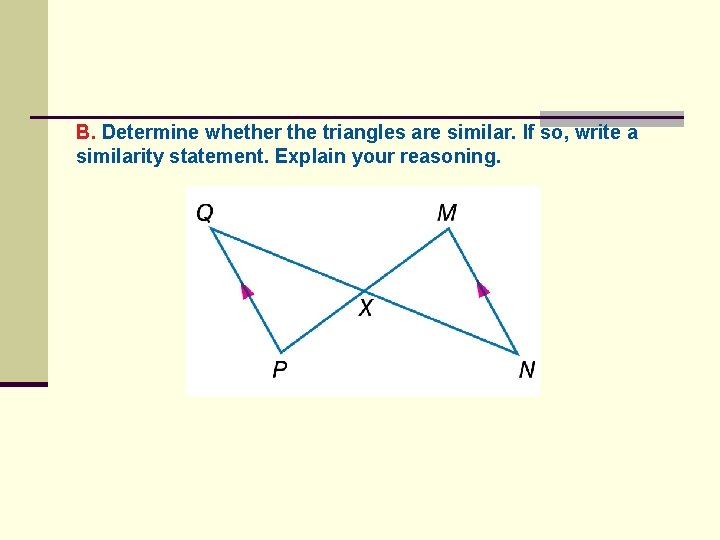
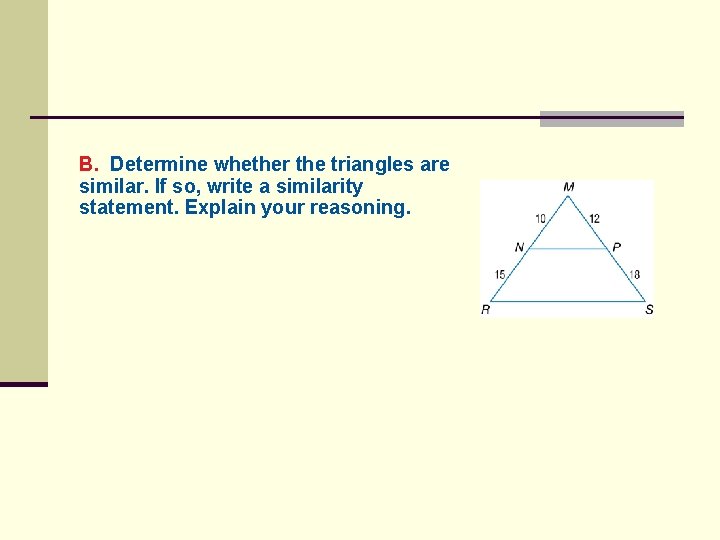
B. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

A. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

B. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

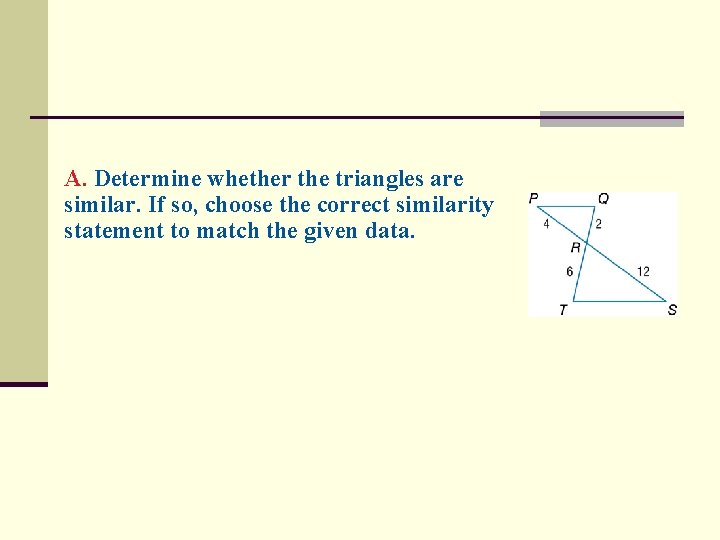
A. Determine whether the triangles are similar. If so, choose the correct similarity statement to match the given data.

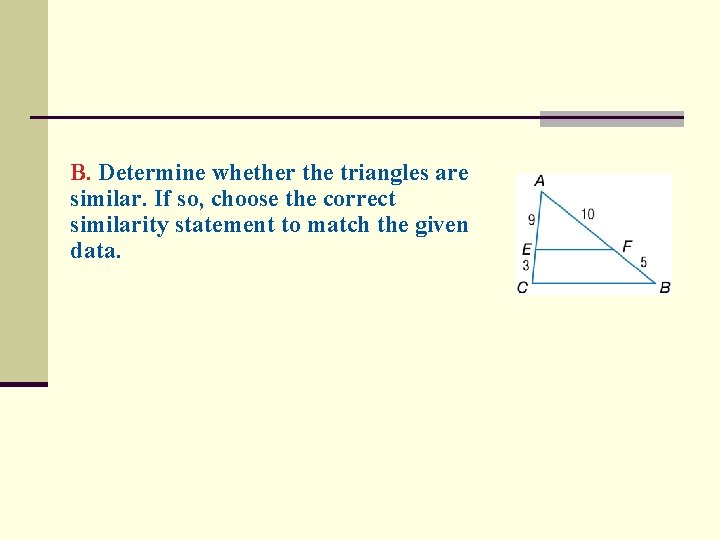
B. Determine whether the triangles are similar. If so, choose the correct similarity statement to match the given data.

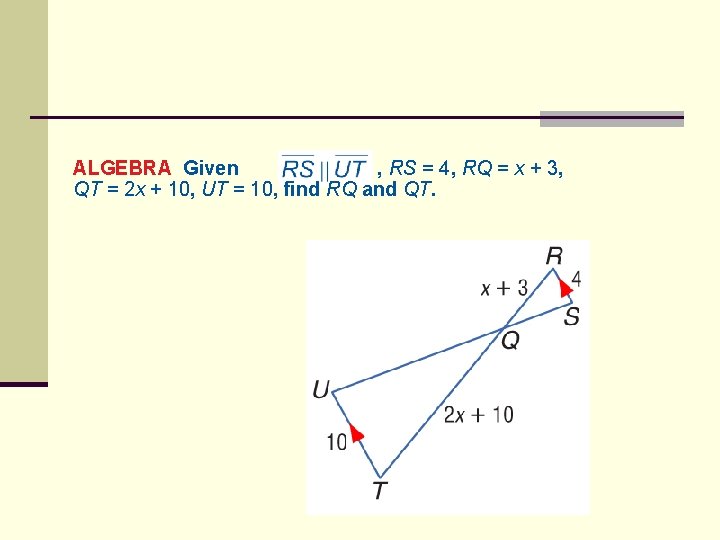
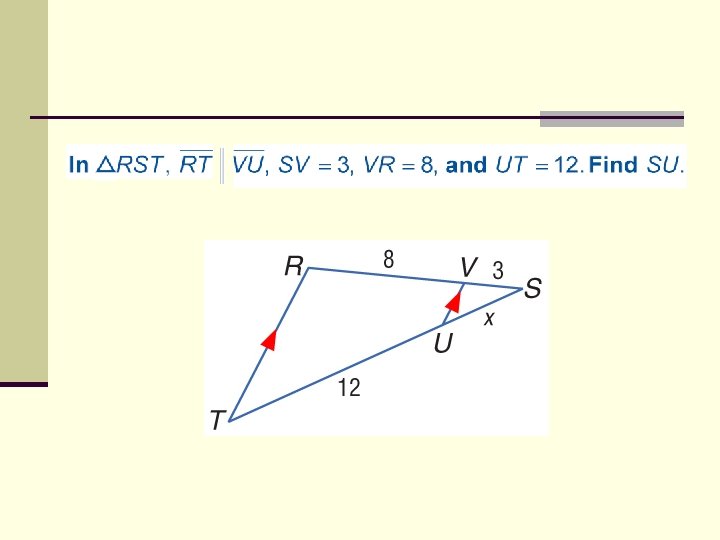
ALGEBRA Given , RS = 4, RQ = x + 3, QT = 2 x + 10, UT = 10, find RQ and QT.

SKYSCRAPERS Josh wanted to measure the height of the Sears Tower in Chicago. He used a 12 -foot light pole and measured its shadow at 1 p. m. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at the same time. What is the height of the Sears Tower?

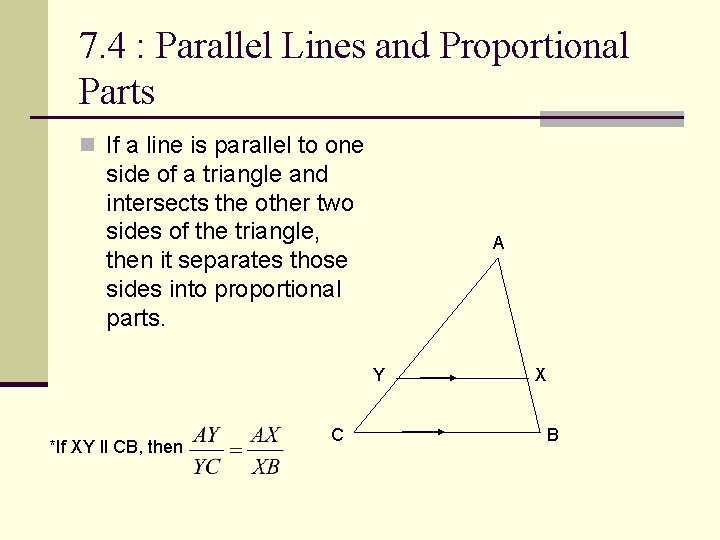
7. 4 : Parallel Lines and Proportional Parts n If a line is parallel to one side of a triangle and intersects the other two sides of the triangle, then it separates those sides into proportional parts. A Y *If XY ll CB, then C X B

7. 4 : Parallel Lines and Proportional Parts n Triangle Midsegment Theorem n A midsegment of a triangle is parallel to one side of a triangle, and its length is half of the side that it is parallel to *If E and B are the midpoints of AD and AC respectively, then EB = DC A E D B C

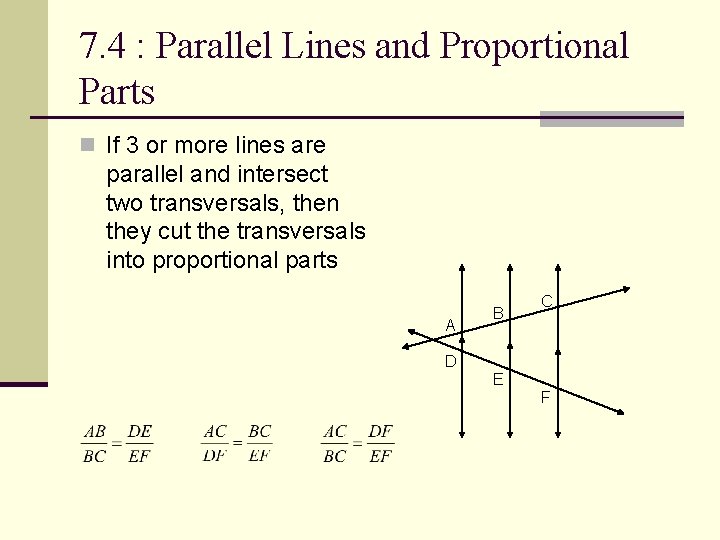
7. 4 : Parallel Lines and Proportional Parts n If 3 or more lines are parallel and intersect two transversals, then they cut the transversals into proportional parts A B C D E F

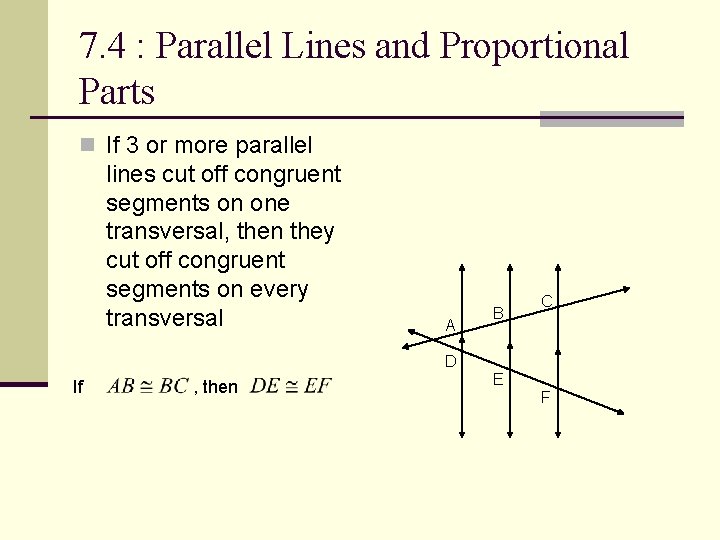
7. 4 : Parallel Lines and Proportional Parts n If 3 or more parallel lines cut off congruent segments on one transversal, then they cut off congruent segments on every transversal A B C D If , then E F

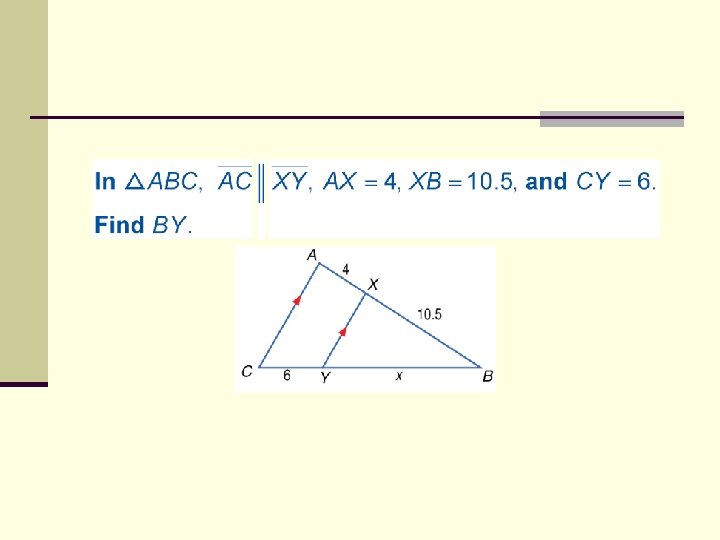
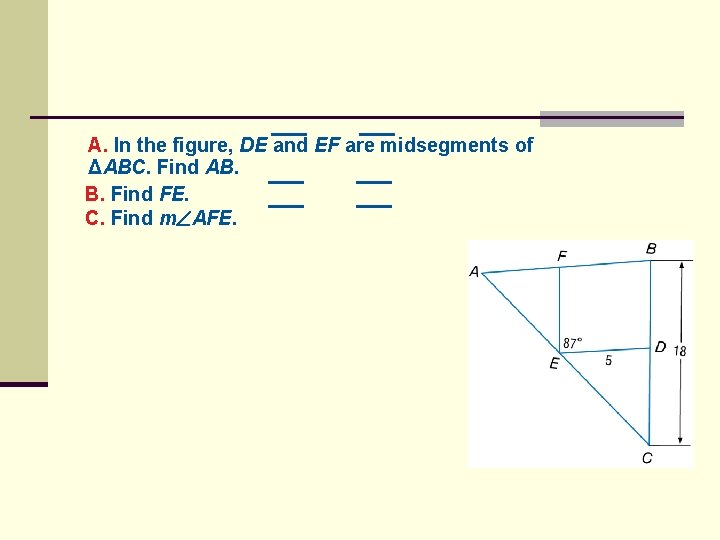
A. In the figure, DE and EF are midsegments of ΔABC. Find AB. B. Find FE. C. Find m AFE.

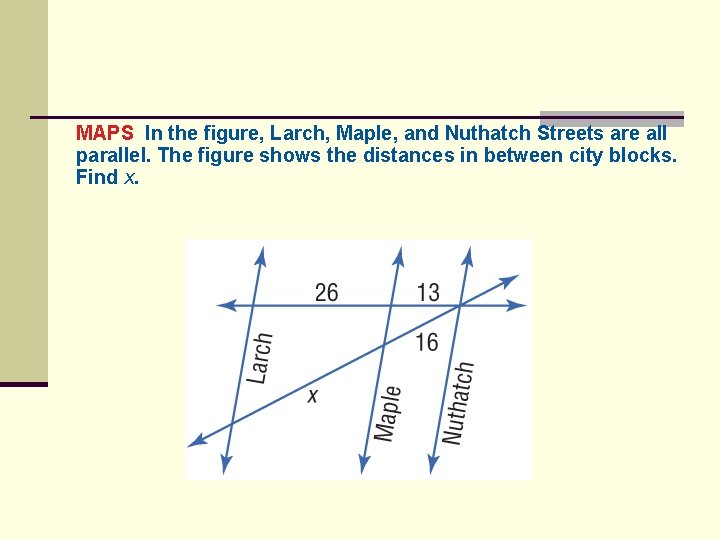
MAPS In the figure, Larch, Maple, and Nuthatch Streets are all parallel. The figure shows the distances in between city blocks. Find x.

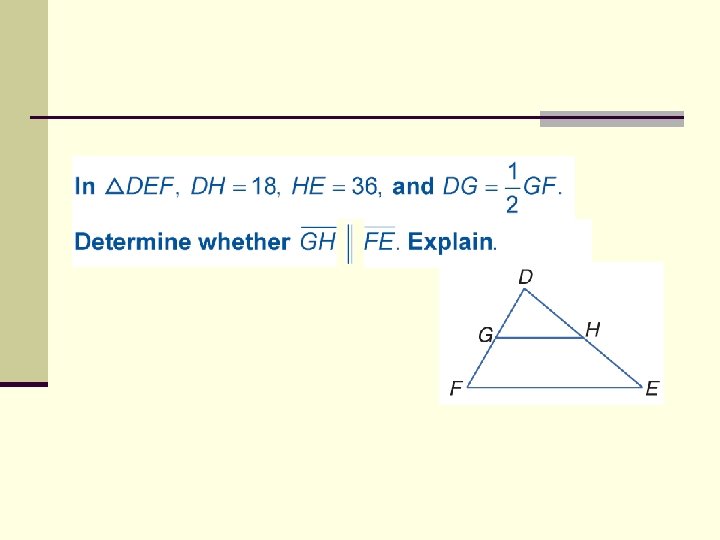
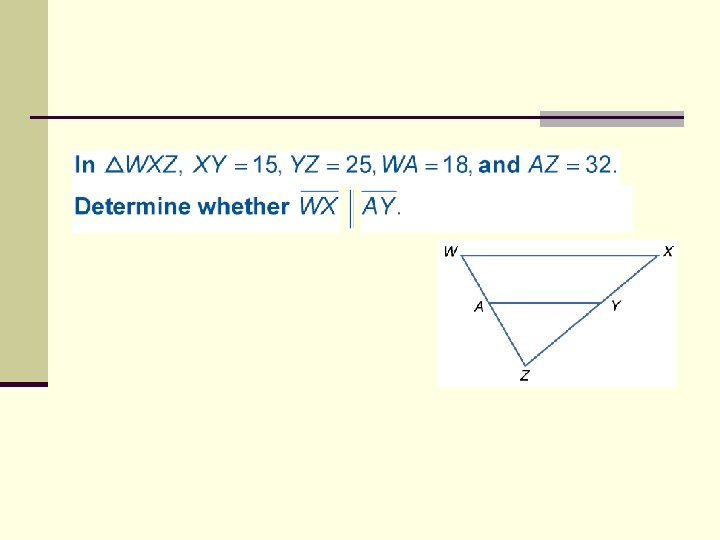
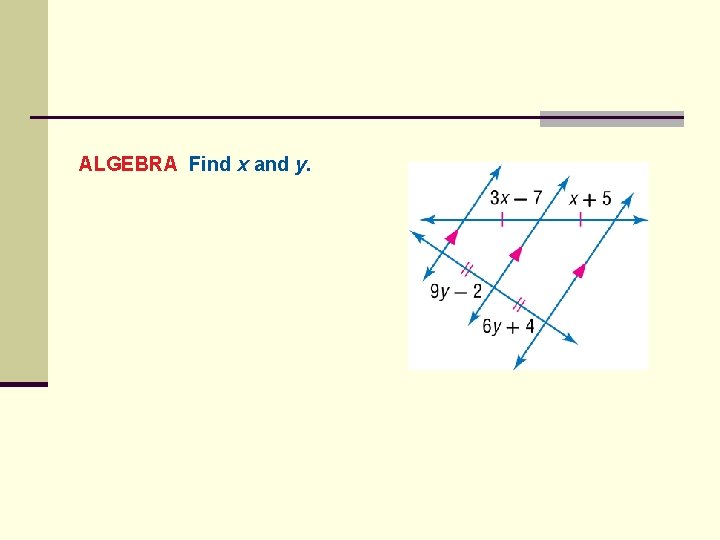
ALGEBRA Find x and y.

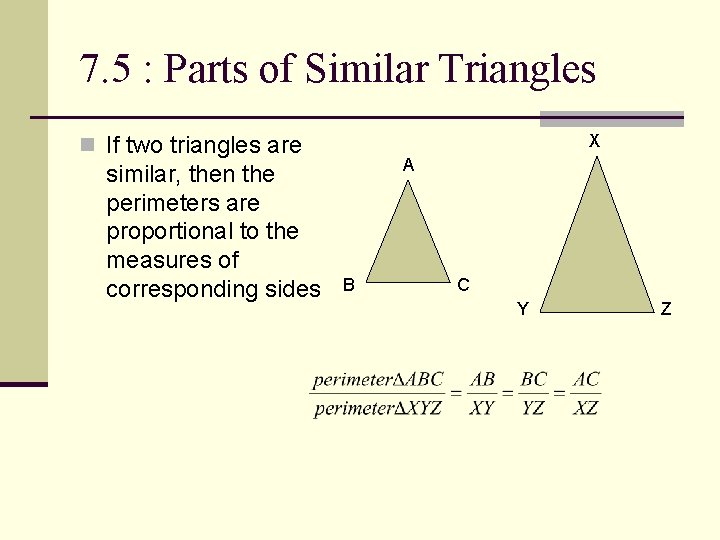
7. 5 : Parts of Similar Triangles X n If two triangles are similar, then the perimeters are proportional to the measures of corresponding sides A B C Y Z

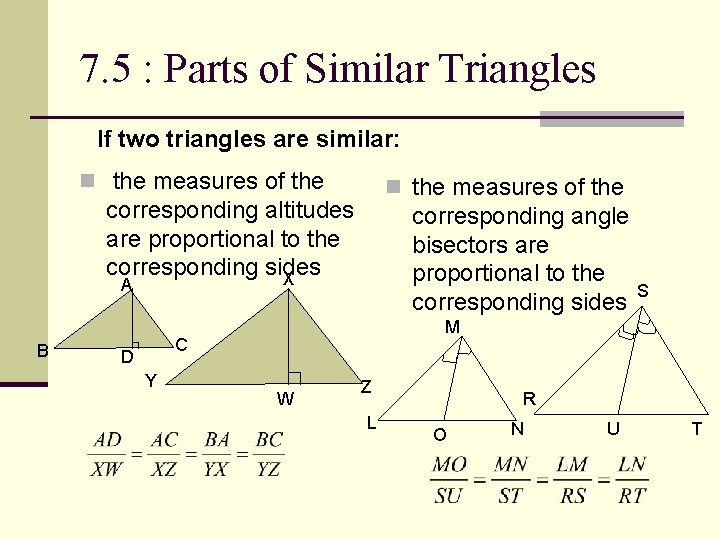
7. 5 : Parts of Similar Triangles If two triangles are similar: n the measures of the corresponding altitudes are proportional to the corresponding sides X corresponding angle bisectors are proportional to the corresponding sides A B M C D Y S W Z L R O N U T

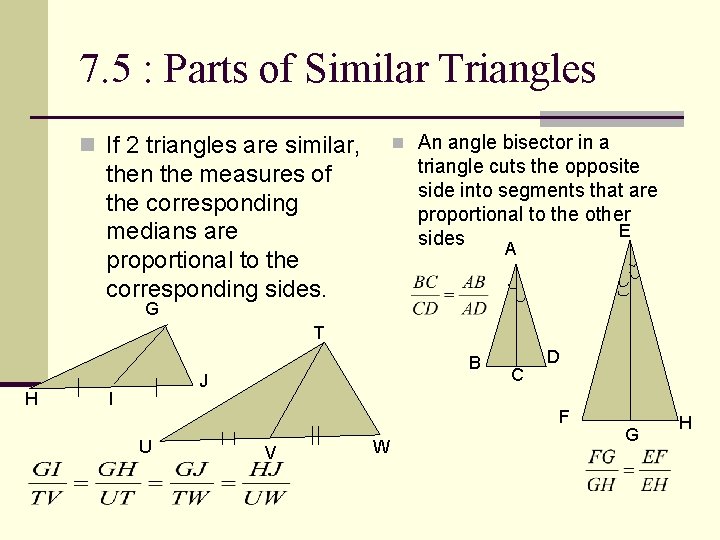
7. 5 : Parts of Similar Triangles n An angle bisector in a n If 2 triangles are similar, triangle cuts the opposite side into segments that are proportional to the other E sides then the measures of the corresponding medians are proportional to the corresponding sides. A G T H B J I C D F U V W G H

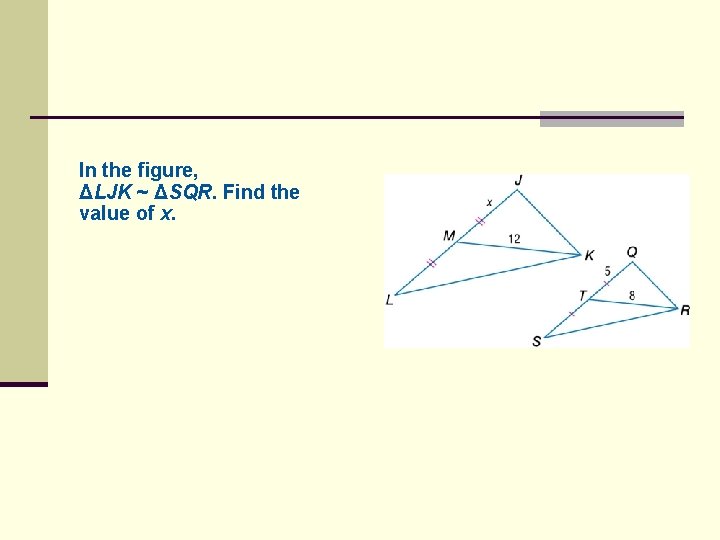
In the figure, ΔLJK ~ ΔSQR. Find the value of x.

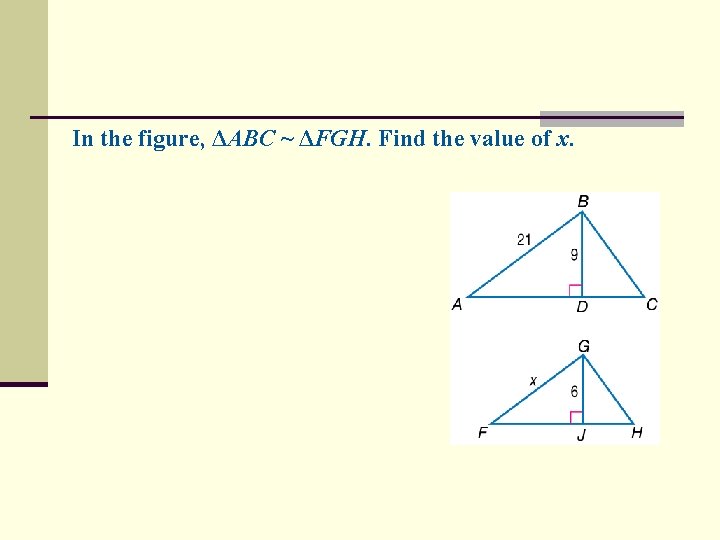
In the figure, ΔABC ~ ΔFGH. Find the value of x.

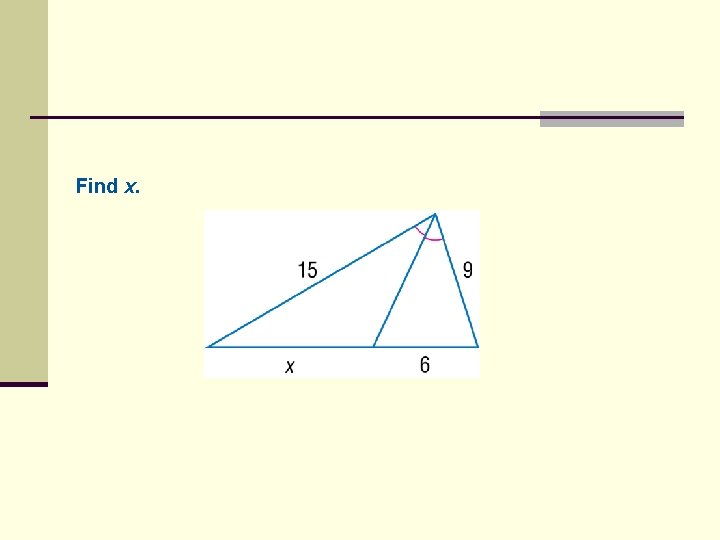
Find x.

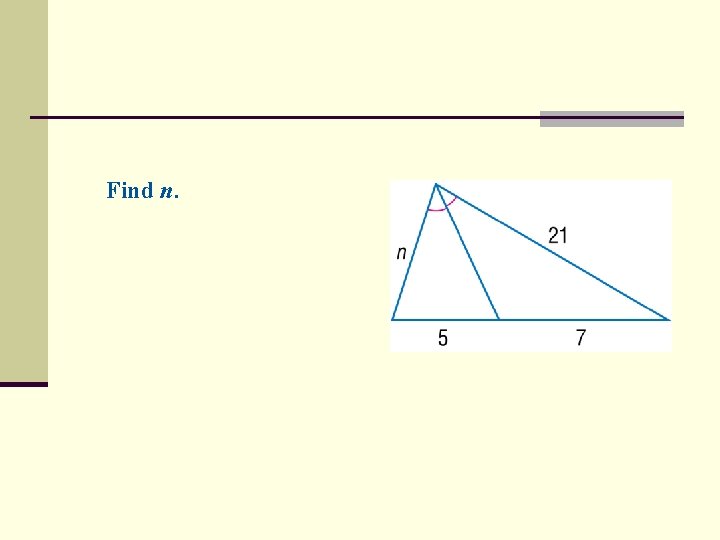
Find n.