Extensive Game with Imperfect Information Part I Strategy

Extensive Game with Imperfect Information Part I: Strategy and Nash equilibrium

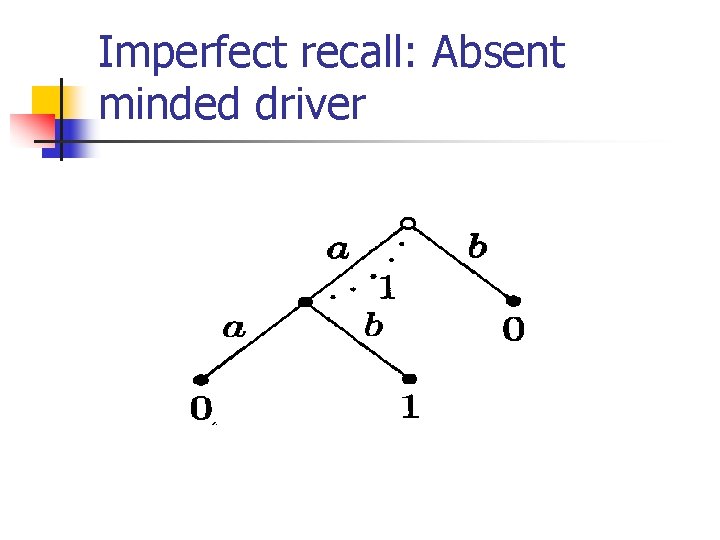
Adding new features to extensive games: n A player does not know actions taken earlier n non-observable actions taken by other players The player has imperfect recall--e. g. absent minded driver The “type” of a player is unknown to others (nature’s choice is nonobservable to other players)

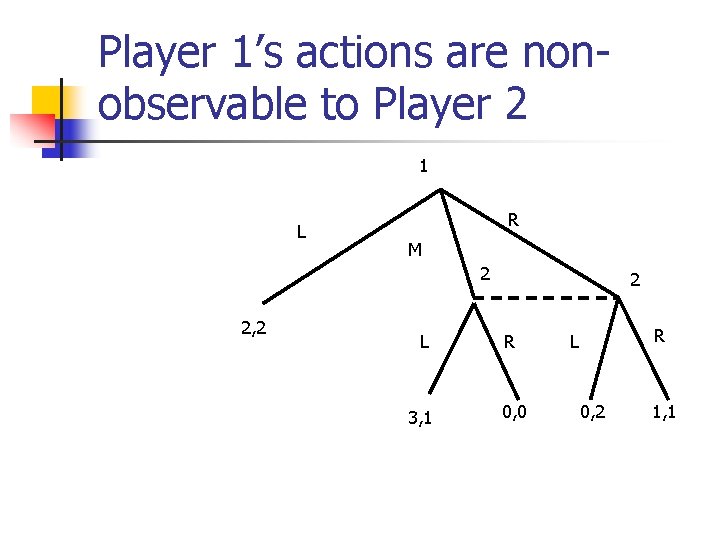
Player 1’s actions are nonobservable to Player 2 1 L R M 2 2, 2 2 L R 3, 1 0, 0 R L 0, 2 1, 1

Imperfect recall: Absent minded driver

Nature’s choice is unknown to third party 1, 1 0, -1 -2, -1 hire 1, 2 No hire 2 MBA No MBA hire No hire 2 0, -3 1/2 high c 1/2 low 2 No hire 0, 0 hire -2, 2 MBA 1 No MBA 2 No hire 0, 0

Extensive game with imperfect information and chances n Definition: An extensive game <N, H, P, fc, (Ti), (ui)> consists of n a set of players N n a set of sequences H n a function (the player function P) that assigns either a player or "chance" to every non-terminal history n A function fc that associates with every history h for which P(h)=c a probability distribution fc(. |h) on A(h), where each such probability distribution is independent of every other such distribution. n For each player i, Ti is an information partition and I i (an element of Ti) is an information set of player i. n For each i, a utility function ui.

Strategies n n DEFINITION: A (pure) strategy of player i in an extensive game is a function that assigns to each of i's information sets Ii an action in A(Ii) (the set of actions available to player i at the information set Ii). DEFINITION: A mixed strategy of player i in an extensive game is a probability distribution over the set of player i’s pure strategies.

Behavioral strategy n DEFINITION. A behavioral strategy of player i in an extensive game is a function that assigns to each of i's information sets Ii a probability distribution over the actions in A(Ii), with the property that each probability distribution is independent of every other distribution.

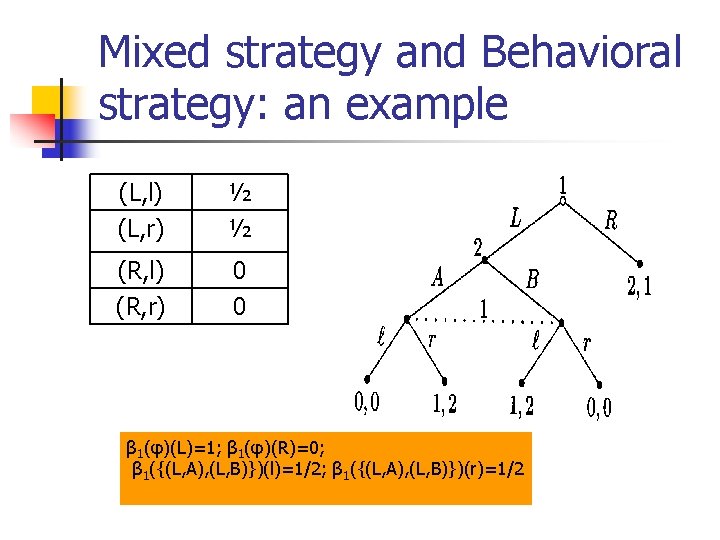
Mixed strategy and Behavioral strategy: an example (L, l) (L, r) ½ ½ (R, l) (R, r) 0 0 β 1(φ)(L)=1; β 1(φ)(R)=0; β 1({(L, A), (L, B)})(l)=1/2; β 1({(L, A), (L, B)})(r)=1/2

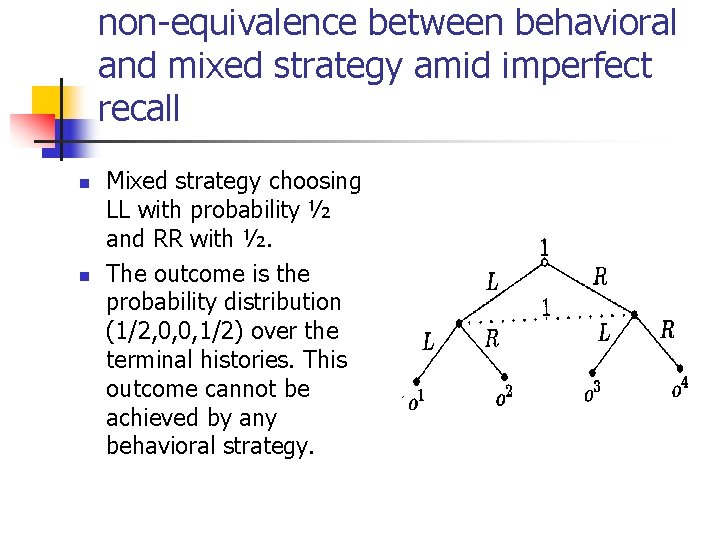
non-equivalence between behavioral and mixed strategy amid imperfect recall n n Mixed strategy choosing LL with probability ½ and RR with ½. The outcome is the probability distribution (1/2, 0, 0, 1/2) over the terminal histories. This outcome cannot be achieved by any behavioral strategy.

Equivalence between behavioral and mixed strategy amid perfect recall n Proposition. For any mixed strategy of a player in a finite extensive game with perfect recall there is an outcome-equivalent behavioral strategy.

Nash equilibrium n n DEFINITION: The Nash equilibrium in mixed strategies is a profile σ* of mixed strategies so that for each player i, ui(O(σ*-i, σ*i))≥ ui(O(σ*-i, σi)) for every σi of player i. A Nash equilibrium in behavioral strategies is defined analogously.

Part II: Belief and Sequential Equilibrium

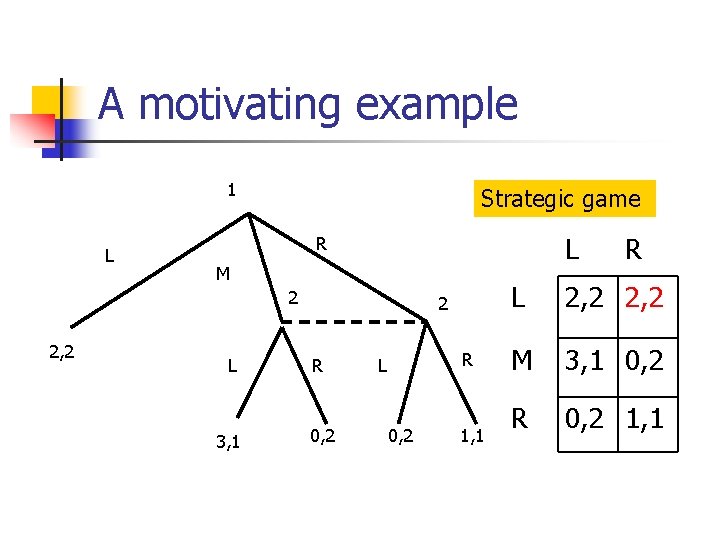
A motivating example 1 L Strategic game L R M 2 2, 2 2 L R 3, 1 0, 2 R L 0, 2 1, 1 R L 2, 2 M 3, 1 0, 2 R 0, 2 1, 1

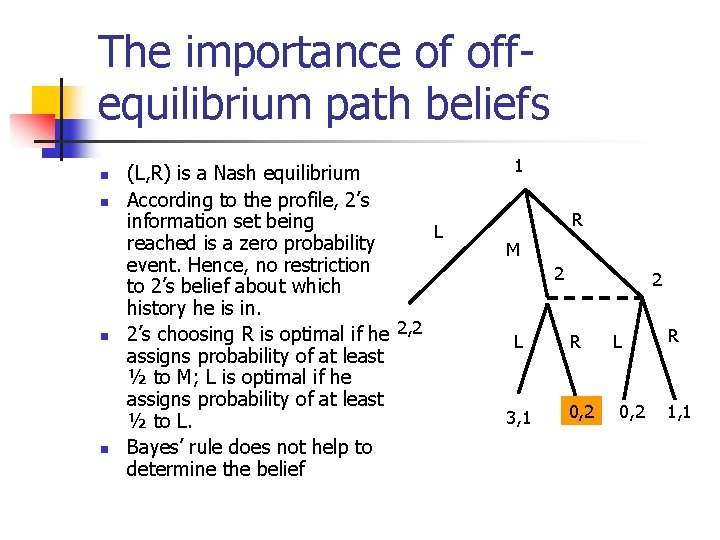
The importance of offequilibrium path beliefs n n (L, R) is a Nash equilibrium According to the profile, 2’s information set being L reached is a zero probability event. Hence, no restriction to 2’s belief about which history he is in. 2’s choosing R is optimal if he 2, 2 assigns probability of at least ½ to M; L is optimal if he assigns probability of at least ½ to L. Bayes’ rule does not help to determine the belief 1 R M 2 L 3, 1 2 R 0, 2 L 0, 2 R 1, 1

belief n n n From now on, we will restrict our attention to games with perfect recall. Thus a sensible equilibrium concept should consist of two components: strategy profile and belief system. For extensive games with imperfect information, when a player has the turn to move in a non-singleton information set, his optimal action depends on the belief he has about which history he is actually in. DEFINITION. A belief system μ in an extensive game is a function that assigns to each information set a probability distribution over the histories in that information set. DEFINITION. An assessment in an extensive game is a pair (β, μ) consisting of a profile of behavioral strategies and a belief system.

Sequential rationality and consistency n It is reasonable to require that n Sequential rationality. Each player's strategy is optimal whenever she has to move, given her belief and the other players' strategies. n Consistency of beliefs with strategies (CBS). Each player's belief is consistent with the strategy profile, i. e. , Bayes’ rule should be used as long as it is applicable.

Perfect Bayesian equilibrium n Definition: An assessment (β, μ) is a perfect Bayesian equilibrium (PBE) (a. k. a. weak sequential equilibrium) if it satisfies both sequential rationality and CBS. n n n Hence, no restrictions at all on beliefs at zeroprobability information set In EGPI, the strategy profile in any PBE is a SPE The strategy profile in any PBE is a Nash equilibrium

Sequential equilibrium n n n Definition. An assessment (β, μ) is consistent if there is a sequence ((βn, μn))n=1, … of assessments that converge to (β, μ) and has the properties that each βn is completely mixed and each μn is derived from using Bayes’ rule. Remark: Consistency implies CBS studied earlier Definition. An assessment is a sequential equilibrium of an extensive game if it is sequentially rational and consistent. n Sequential equilibrium implies PBE n Less easier to use than PBE (need to consider the sequence ((βn, μn))n=1, … )

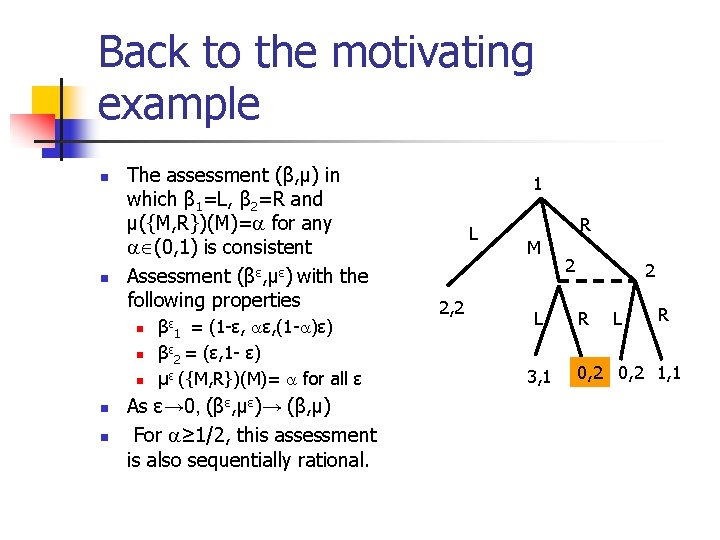
Back to the motivating example n n The assessment (β, μ) in which β 1=L, β 2=R and μ({M, R})(M)= for any (0, 1) is consistent Assessment (βε, με) with the following properties n n n βε 1 = (1 -ε, ε, (1 - )ε) βε 2 = (ε, 1 - ε) με ({M, R})(M)= for all ε As ε→ 0, (βε, με)→ (β, μ) For ≥ 1/2, this assessment is also sequentially rational. 1 L 2, 2 R M L 3, 1 2 2 R L R 0, 2 1, 1

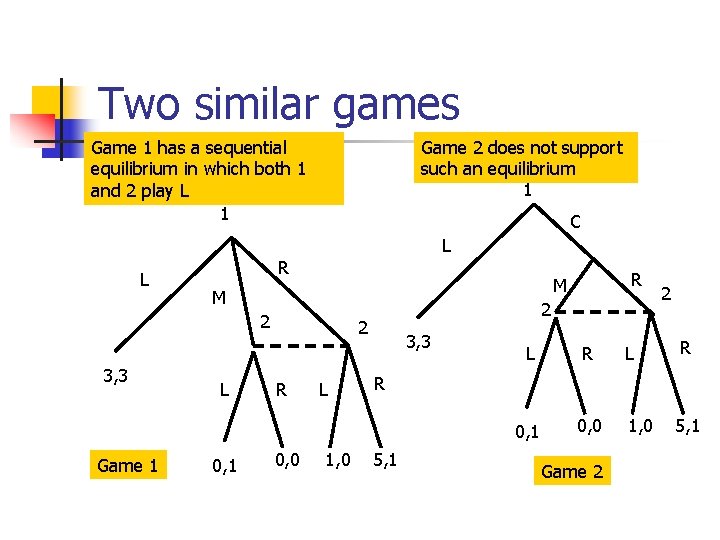
Two similar games Game 1 has a sequential equilibrium in which both 1 and 2 play L 1 L Game 2 does not support such an equilibrium 1 C L R M 2 3, 3 Game 1 L 0, 1 2 2 R 0, 0 R M L 1, 0 3, 3 2 L R 0, 1 0, 0 1, 0 5, 1 R 5, 1 Game 2

Structural consistency n n n Definition. The belief system in an extensive game is structurally consistent if for each information set I there is a strategic profile with the properties that I is reached with positive probability under and is derived from using Bayes’ rule. Remark: Note that different strategy profiles may be needed to justify the beliefs at different information sets. Remark: There is no straightforward relationship between consistency and structural consistency. (β, μ) being consistent is neither sufficient nor necessary for μ to be structurally consistent.

Signaling games n n n A signaling game is an extensive game with the following simple form. Two players, a “sender’ and a “receiver. ” The sender knows the value of an uncertain parameter and then chooses an action m (message) The receiver observes the message (but not the value of ) and takes an action a. Each player’s payoff depends upon the value of , the message m, and the action a taken by the receiver.

Signaling games n Two types n n Signals are (directly) costly Signals are directly not costly – cheap talk game

Spence’s education game n n n Players: worker (1) and firm (2) 1 has two types: high ability H with probability p H and low ability L with probability p L. The two types of worker choose education level e H and e L (messages). The firm also choose a wage w equal to the expectation of the ability The worker’s payoff is w – e/

Pooling equilibrium n n n e H = e L = e* L p. H ( H - L) w* = p. H H + p. L L Belief: he who chooses a different e is thought with probability one as a low type Then no type will find it beneficial to deviate. Hence, a continuum of perfect Bayesian equilibria

Separating equilibrium n n n e L= 0 H ( H - L) ≥ e H ≥ L ( H - L) w H = H and w L = L Belief: he who chooses a different e is thought with probability one as a low type Again, a continuum of perfect Bayesian equilibria Remark: all these (pooling and separating) perfect Bayesian equilibria are sequential equilibria as well.

When does signaling work? n n The signal is costly Single crossing condition holds (i. e. , signal is more costly for the low-type than for the hightype)

Refinement of sequential equilibrium n n There are too many sequential equilibria in the education game. Are some more appealing than others? Cho-Kreps intuitive criterion n A refinement of sequential equilibrium —not every sequential equilibrium satisfies this criterion

An example where a sequential equilibrium is unreasonable n n n Two sequential equilibria with outcomes: (R, R) and (L, L), respectively (L, L) is supported by belief that, in case 2’s information set is reached, with high probability 1 chose M. If 2’s information set is reached, 2 may think “since M is strictly dominated by L, it is not rational for 1 to choose M and hence 1 must have chosen R. ” 1 L 2, 2 R M L 1, 3 2 2 R 0, 0 L 0, 0 R 5, 1

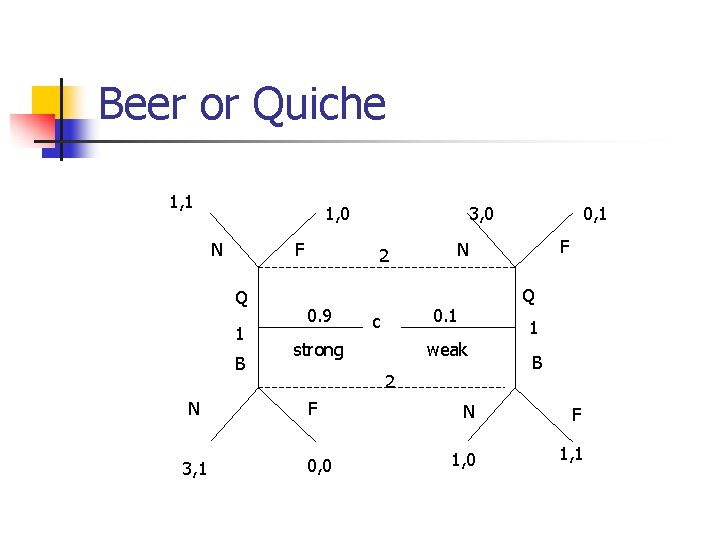
Beer or Quiche 1, 1 1, 0 N F Q 1 B N 3, 1 3, 0 2 0. 9 strong Q 1 weak 2 F 0, 0 F N 0. 1 c 0, 1 B N F 1, 0 1, 1

Why the second equilibrium is not reasonable? n n n If player 1 is weak she should realize that the choice for B is worse for her than following the equilibrium, whatever the response of player 2. If player 1 is strong and if player 2 correctly concludes from player 1 choosing B that she is strong and hence chooses N, then player 1 is indeed better than she is in the equilibrium. Hence player 2’s belief is unreasonable and the equilibrium is not appealing under scrutiny. 1, 1 1, 0 N F Q 1 B 3, 0 2 0. 9 c strong F 3, 1 0, 0 F N 0. 1 weak 2 N 0, 1 Q 1 B N F 1, 0 1, 1

Spence’s education game n n n All the pooling equilibria are eliminated by the Cho-Kreps intuitive criterion. Let e satisfy w* – e*/ L > H – e/ L and w* – e*/ H > H – e/ L (such a value of e clearly exists. ) If a high type work deviates and chooses e and is correctly viewed as a good type, then she is better off than under the pooling equilibrium If a low type work deviates and successfully convinces the firm that she is a high type, still she is worse off than under the pooling equilibrium. Hence, according to the intuitive criterion, the firm’s belief upon such a deviation should construe that the deviator is a high type rather than a low type. The pooling equilibrium break down!

Spence’s education game n n n Only one separating equilibrium survives the Cho. Kreps Intuitive criterion, namely: e L = 0 and e H = L ( H - L) Why a separating equilibrium is killed where e L = 0 and e H > L ( H - L)? A high type worker after choosing an e slightly smaller will benefit from it if she is correctly construed as a high type. A low type worker cannot benefit from it however. Hence, this separating equilibrium does not survive Cho-Kreps intuitive criterion.