EQUAZIONI ESPONENZIALI Una equazione in cui lincognita compare











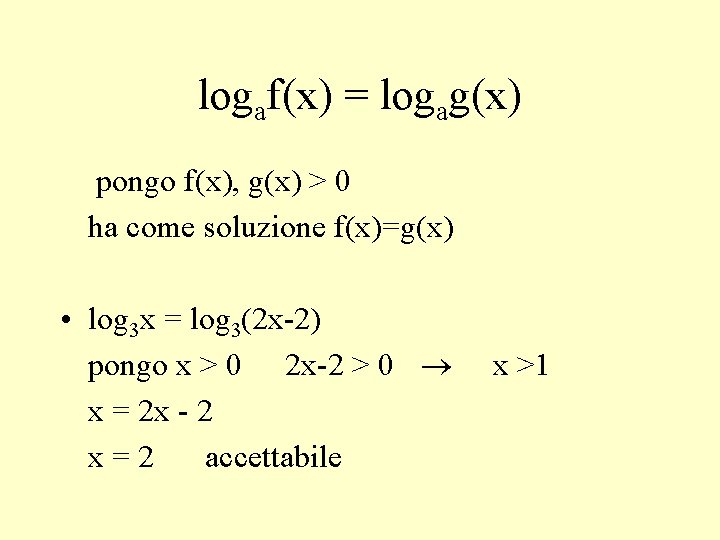


- Slides: 15

EQUAZIONI ESPONENZIALI • Una equazione in cui l’incognita compare all’esponente di almeno un numero reale positivo e diverso da 1. • Vediamo i principali tipi di equazioni esponenziali.

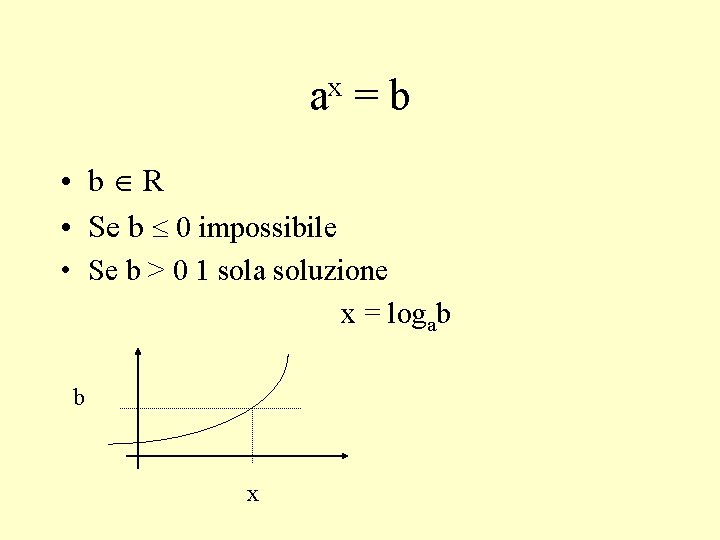
x a =b • b R • Se b 0 impossibile • Se b > 0 1 sola soluzione x = logab b x

ESEMPI • 3 x = 8 x = log 38 • 2 x = 5 x = log 25

ALTRI CASI • af(x)=ag(x) ha come soluzione f(x)=g(x) Esempi: • 2 x = 4 2 x = 22 x=2

ESEMPI • 4 x = 32 22 x = 25 x = 5/2 • 5 x = 0. 04 5 x = 4/100 5 x = 1/25 5 x = 5 -2 x = -2

x f(a )=0 si pone ax = t si risolve f(t) = 0 supponiamo che le soluzioni, se esistono, siano t 1, … , tn si risolvono le equazioni: ax = t 1 , …, ax = tn

ESEMPI • 9 x = 2· 3 x 32 x = 2 · 3 x 3 x= t t 2 = 2 ·t t(t - 2) = 0 t = 0, t = 2 3 x = 0 mai 3 x = 2 x = log 32

af(x) = bg(x) ci si riconduce al caso precedente scrivendo: E quindi, eguagliando gli esponenti: f(x)=g(x)loga(b)

ESEMPI 52 x = 23 x+1 2 x = log 52(3 x + 1) 2 x = (3 x + 1)log 52 x (2 - 3 log 52) = log 52 x = log 52 / (2 - 3 log 52)

EQUAZIONI LOGARITMICHE • Una equazione in cui l’incognita compare nell’argomento di un logaritmo. • Vediamo i principali tipi di equazioni logaritmiche.

logax = b x>0 b R x = ab • Esempio: log 3 x = 2 x>0 x = 32 = 9 accettabile

logaf(x) = b pongo f(x) > 0 f(x) = ab • Esempio: log 2 (4 x) = 2 pongo 4 x > 0 x>0 4 x = 22 x = 1 accettabile
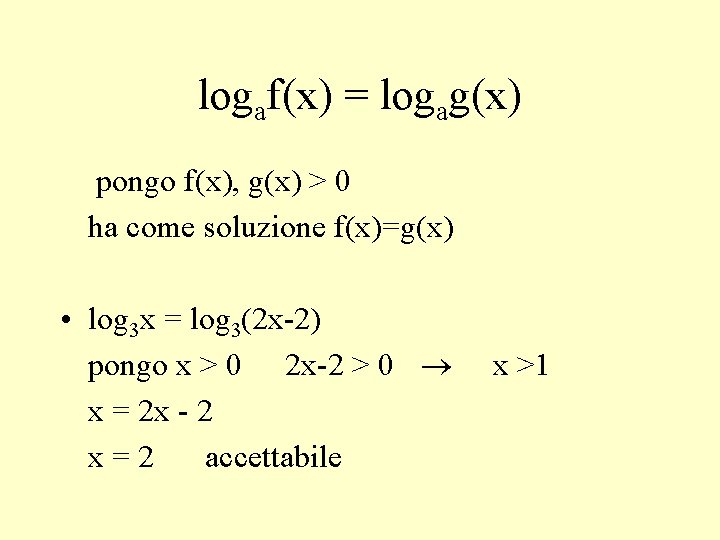
logaf(x) = logag(x) pongo f(x), g(x) > 0 ha come soluzione f(x)=g(x) • log 3 x = log 3(2 x-2) pongo x > 0 2 x-2 > 0 x = 2 x - 2 x=2 accettabile x >1

f( loga(x) )=0 si pone loga(x) = t si risolve f(t) = 0 supponiamo che le soluzioni, se esistono, siano t 1, … , tn si risolvono le equazioni: loga(x) = t 1 , …, loga(x) = tn

ESEMPI • ln 2(x) – 2 ln(x) - 3 = 0 x>0 pongo ln(x) = t t 2 – 2 t – 3 = 0 t 1 = 3 t 2 = - 1 ln(x) = 3 x = e 3 accettabile ln(x) = - 1 x = e-1 accettabile
 Esercizi sui logaritmi zanichelli
Esercizi sui logaritmi zanichelli Funzione esponenziale esercizi
Funzione esponenziale esercizi Esponente reale
Esponente reale Disequazioni esponenziali
Disequazioni esponenziali Mappa rette parallele e perpendicolari
Mappa rette parallele e perpendicolari Piano cartesiano mappa concettuale
Piano cartesiano mappa concettuale Swt eclipse
Swt eclipse Gui tui
Gui tui Cui//sp-prvcy
Cui//sp-prvcy Chestermere recycling depot
Chestermere recycling depot Teng cui
Teng cui Lisa cui
Lisa cui I due rami in cui si biforca la trachea
I due rami in cui si biforca la trachea Eruzione peleeana
Eruzione peleeana Interoperability in healthcare
Interoperability in healthcare Executive order 13556
Executive order 13556