Electronic Instrumentation Experiment 2 Part A Intro to











































- Slides: 61

Electronic Instrumentation Experiment 2 * Part A: Intro to Transfer Functions and AC Sweeps * Part B: Phasors, Transfer Functions and Filters * Part C : Using Transfer Functions and RLC Circuits * Part D: Equivalent Impedance and DC Sweeps

Part A Introduction to Transfer Functions and Phasors w Complex Polar Coordinates w Complex Impedance (Z) w AC Sweeps w

Transfer Functions w The transfer function describes the behavior of a circuit at Vout for all possible Vin.

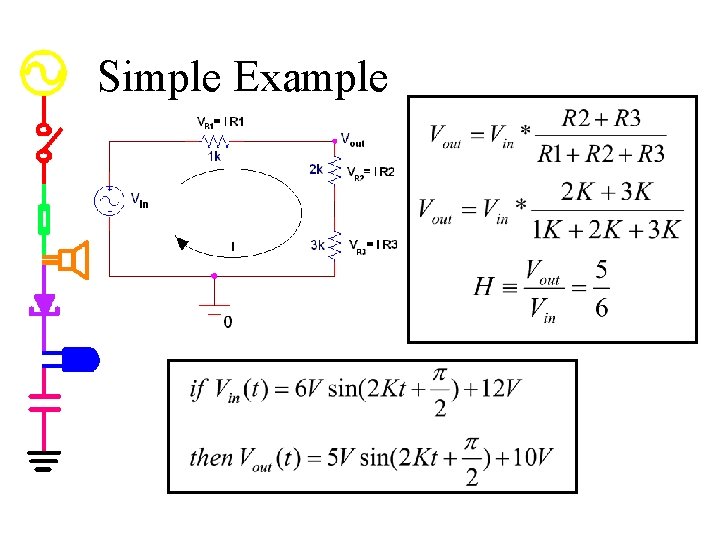
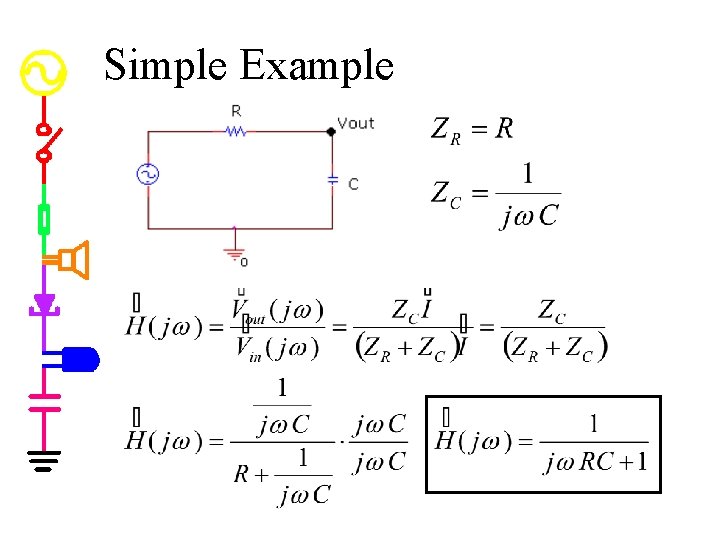
Simple Example

More Complicated Example What is H now? w H now depends upon the input frequency (w = 2 pf) because the capacitor and inductor make the voltages change with the change in current.

How do we model H? We want a way to combine the effect of the components in terms of their influence on the amplitude and the phase. w We can only do this because the signals are sinusoids w • cycle in time • derivatives and integrals are just phase shifts and amplitude changes

We will define Phasors A phasor is a function of the amplitude and phase of a sinusoidal signal w Phasors allow us to manipulate sinusoids in terms of amplitude and phase changes. w Phasors are based on complex polar coordinates. w Using phasors and complex numbers we will be able to find transfer functions for circuits. w

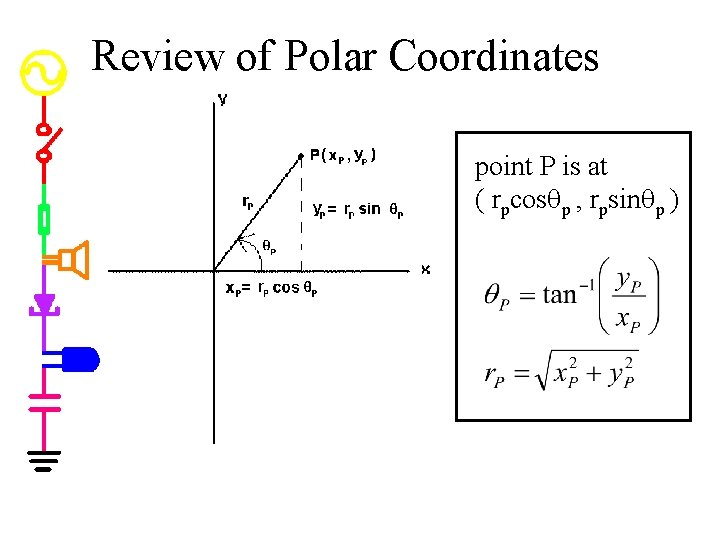
Review of Polar Coordinates point P is at ( rpcosqp , rpsinqp )

Review of Complex Numbers zp is a single number represented by two numbers w zp has a “real” part (xp) and an “imaginary” part (yp) w

Complex Polar Coordinates z = x+jy where x is A cosf and y is A sinf w wt cycles once around the origin once for each cycle of the sinusoidal wave (w=2 pf) w

Now we can define Phasors The real part is our signal. w The two parts allow us to determine the influence of the phase and amplitude changes mathematically. w After we manipulate the numbers, we discard the imaginary part. w

The “V=IR” of Phasors The influence of each component is given by Z, its complex impedance w Once we have Z, we can use phasors to analyze circuits in much the same way that we analyze resistive circuits – except we will be using the complex polar representation. w

Magnitude and Phase w Phasors have a magnitude and a phase derived from polar coordinates rules.

Influence of Resistor on Circuit Resistor modifies the amplitude of the signal by R w Resistor has no effect on the phase w

Influence of Inductor on Circuit Note: cosq=sin(q+p/2) Inductor modifies the amplitude of the signal by w. L w Inductor shifts the phase by +p/2 w

Influence of Capacitor on Circuit Capacitor modifies the amplitude of the signal by 1/w. C w Capacitor shifts the phase by -p/2 w

Understanding the influence of Phase

Complex Impedance w Z defines the influence of a component on the amplitude and phase of a circuit • Resistors: ZR = R • change the amplitude by R • Capacitors: ZC=1/jw. C • change the amplitude by 1/w. C • shift the phase -90 (1/j=-j) • Inductors: ZL=jw. L • change the amplitude by w. L • shift the phase +90 (j)

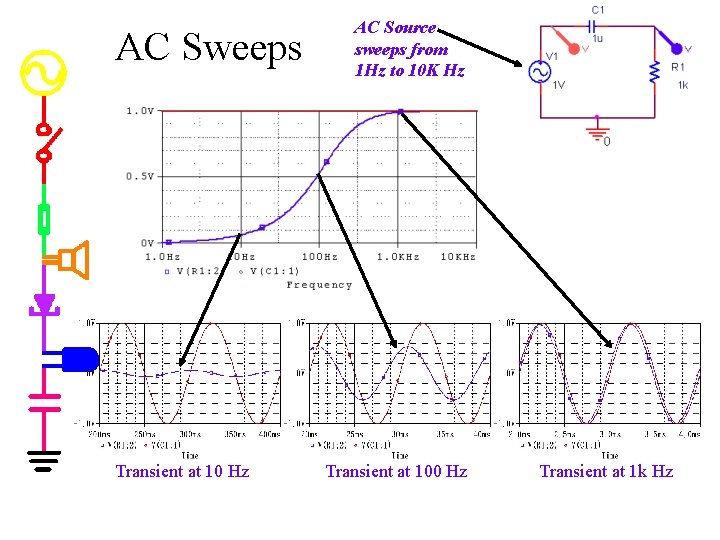
AC Sweeps Transient at 10 Hz AC Source sweeps from 1 Hz to 10 K Hz Transient at 100 Hz Transient at 1 k Hz

Notes on Logarithmic Scales

Capture/PSpice Notes w Showing the real and imaginary part of the signal • in Capture: PSpice->Markers->Advanced • ->Real Part of Voltage • ->Imaginary Part of Voltage • in PSpice: Add Trace • real part: R( ) • imaginary part: IMG( ) w Showing the phase of the signal • in Capture: • PSpice->Markers->Advanced->Phase of Voltage • in PSPice: Add Trace • phase: P( )

Part B Phasors w Complex Transfer Functions w Filters w

Definition of a Phasor The real part is our signal. w The two parts allow us to determine the influence of the phase and amplitude changes mathematically. w After we manipulate the numbers, we discard the imaginary part. w

Phasor References http: //ccrmawww. stanford. edu/~jos/filters/Phasor_Notat ion. html w http: //www. ligo. caltech. edu/~vsanni/ph 3/Ex p. ACCircuits/ACCircuits. pdf w http: //ptolemy. eecs. berkeley. edu/eecs 20/ber keley/phasors/demo/phasors. html w

Phasor Applet

Adding Phasors & Other Applets

Magnitude and Phase w Phasors have a magnitude and a phase derived from polar coordinates rules.

Euler’s Formula

Manipulating Phasors (1) w Note wt is eliminated by the ratio • This gives the phase change between signal 1 and signal 2

Manipulating Phasors (2)

Complex Transfer Functions If we use phasors, we can define H for all circuits in this way. w If we use complex impedances, we can combine all components the way we combine resistors. w H and V are now functions of j and w w

Complex Impedance w Z defines the influence of a component on the amplitude and phase of a circuit • Resistors: ZR = R • Capacitors: ZC=1/jw. C • Inductors: ZL=jw. L w We can use the rules for resistors to analyze circuits with capacitors and inductors if we use phasors and complex impedance.

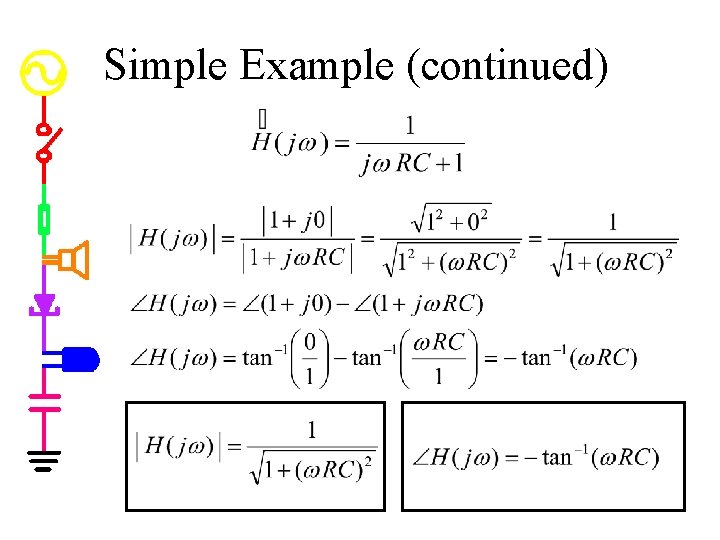
Simple Example

Simple Example (continued)

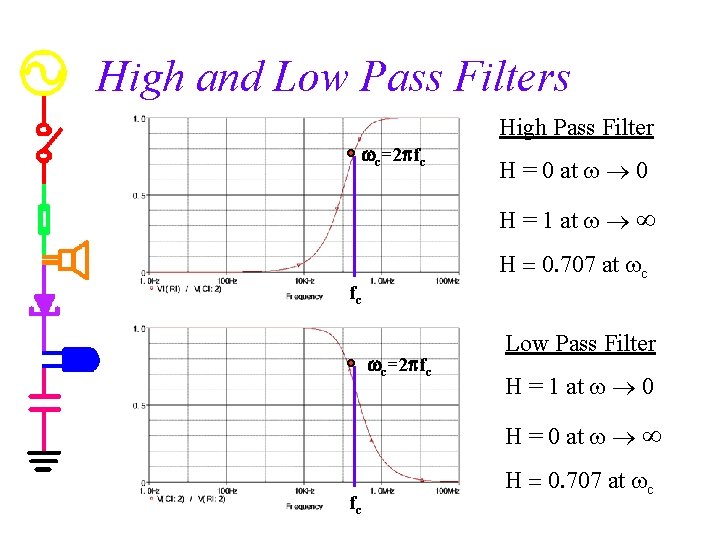
High and Low Pass Filters High Pass Filter wc=2 pfc H = 0 at w ® 0 H = 1 at w ® ¥ H = 0. 707 at wc fc wc=2 pfc Low Pass Filter H = 1 at w ® 0 H = 0 at w ® ¥ fc H = 0. 707 at wc

Corner Frequency The corner frequency of an RC or RL circuit tells us where it transitions from low to high or visa versa. w We define it as the place where w w For RC circuits: w For RL circuits:

Corner Frequency of our example

H(jw), wc, and filters We can use the transfer function, H(jw), and the corner frequency, wc, to easily determine the characteristics of a filter. w If we consider the behavior of the transfer function as w approaches 0 and infinity and look for when H nears 0 and 1, we can identify high and low pass filters. w The corner frequency gives us the point where the filter changes: w

Taking limits w At low frequencies, (ie. w=10 -3), lowest power of w dominates w At high frequencies (ie. w =10+3), highest power of w dominates

Taking limits -- Example w At low frequencies, (lowest power) w At high frequencies, (highest power)

Our example at low frequencies

Our example at high frequencies

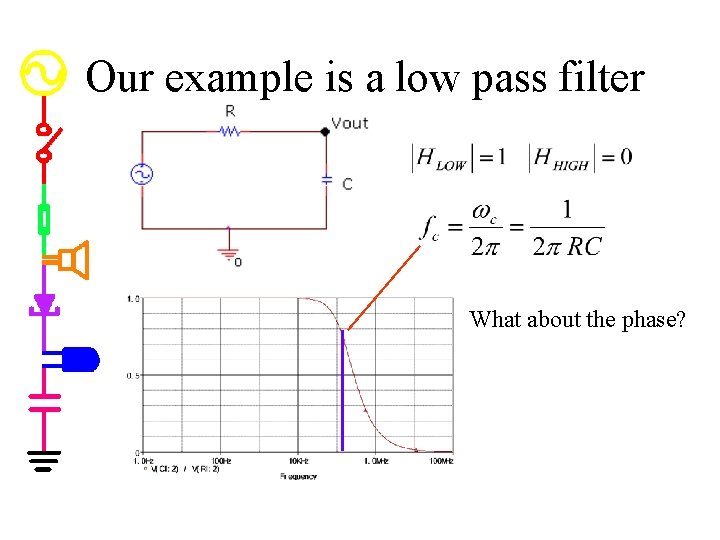
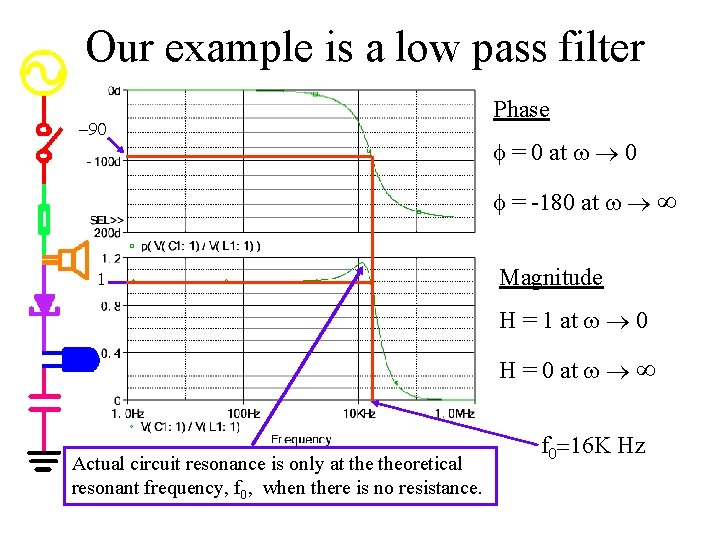
Our example is a low pass filter What about the phase?

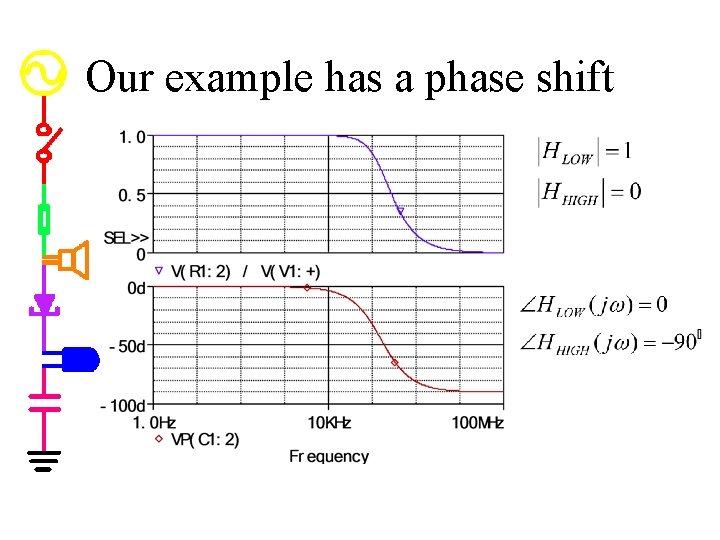
Our example has a phase shift

Part C Using Transfer Functions w Capacitor Impedance Proof w More Filters w Transfer Functions of RLC Circuits w

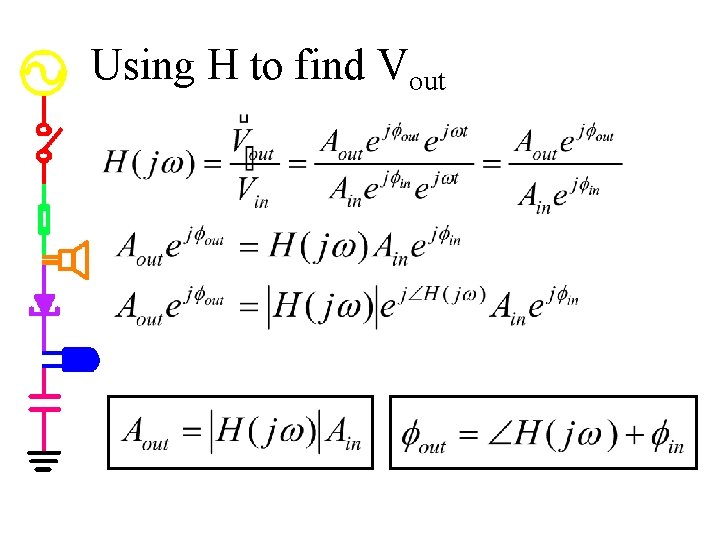
Using H to find Vout

Simple Example (with numbers)

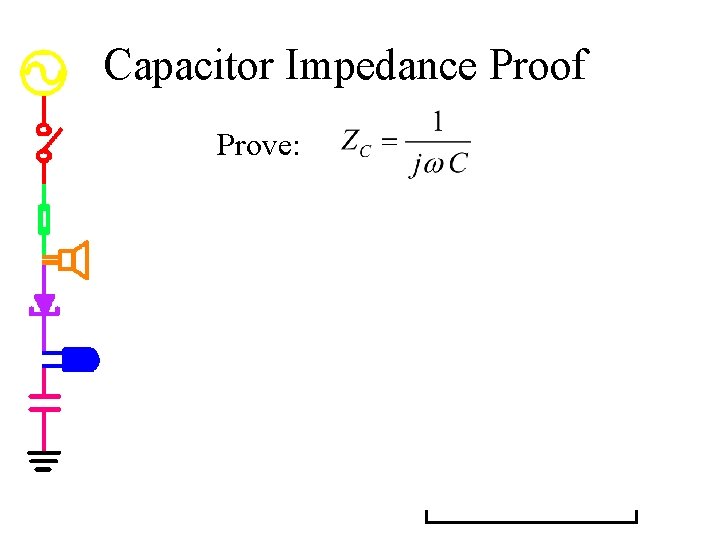
Capacitor Impedance Proof Prove:

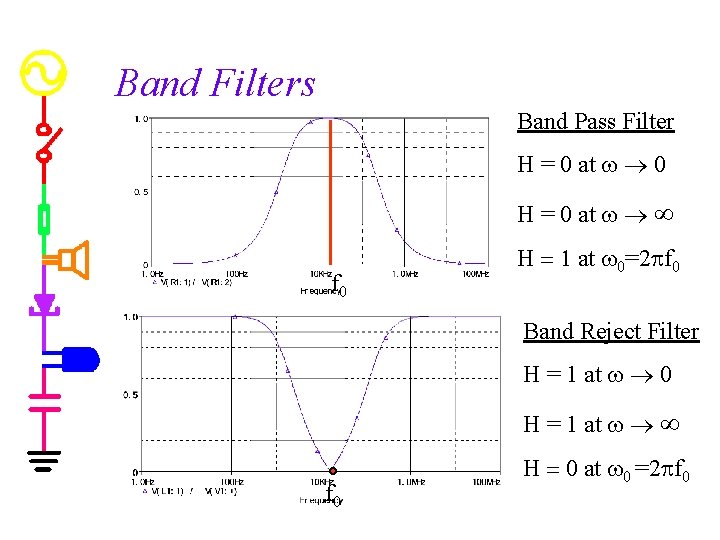
Band Filters Band Pass Filter H = 0 at w ® 0 H = 0 at w ® ¥ f 0 H = 1 at w 0=2 pf 0 Band Reject Filter H = 1 at w ® 0 H = 1 at w ® ¥ f 0 H = 0 at w 0 =2 pf 0

Resonant Frequency The resonant frequency of an RLC circuit tells us where it reaches a maximum or minimum. w This can define the center of the band (on a band filter) or the location of the transition (on a high or low pass filter). w The equation for the resonant frequency of an RLC circuit is: w

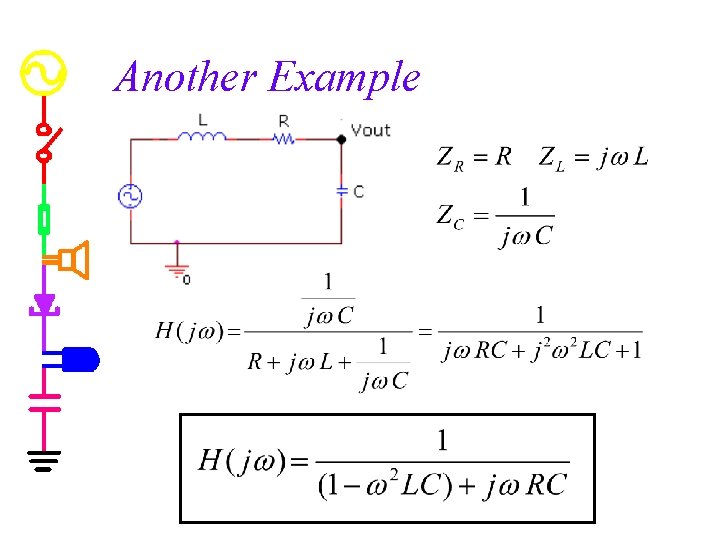
Another Example

At Very Low Frequencies At Very High Frequencies

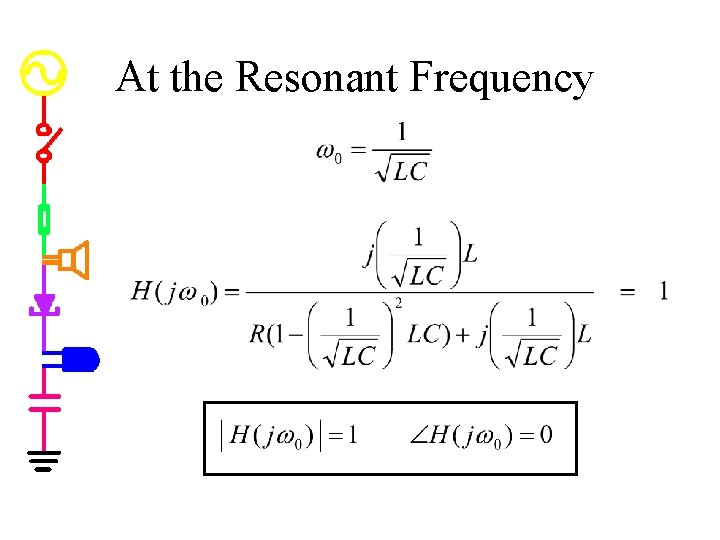
At the Resonant Frequency if L=1 m. H, C=0. 1 u. F and R=100 W w 0=100 K rad/sec f 0=16 K Hz |H 0|=1

Our example is a low pass filter -90 Phase f = 0 at w ® 0 f = -180 at w ® ¥ 1 Magnitude H = 1 at w ® 0 H = 0 at w ® ¥ Actual circuit resonance is only at theoretical resonant frequency, f 0, when there is no resistance. f 0=16 K Hz

Part D Equivalent Impedance w Transfer Functions of More Complex Circuits w

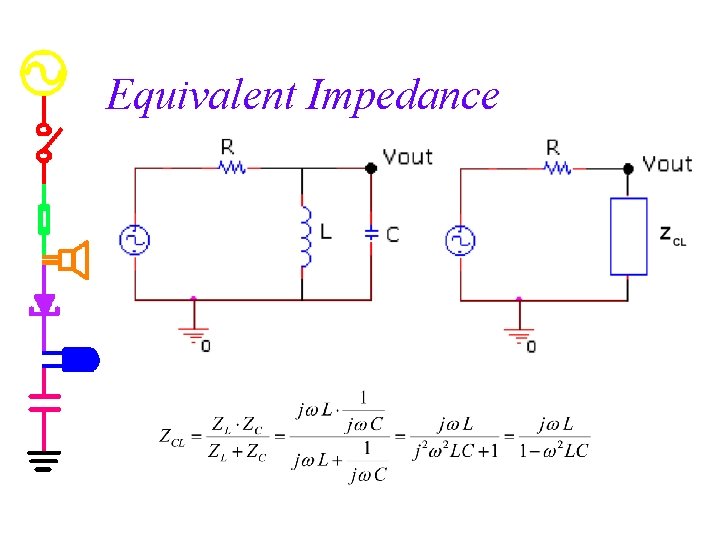
Equivalent Impedance Even though this filter has parallel components, we can still handle it. w We can combine complex impedances like resistors to find the equivalent impedance of the components combined. w

Equivalent Impedance

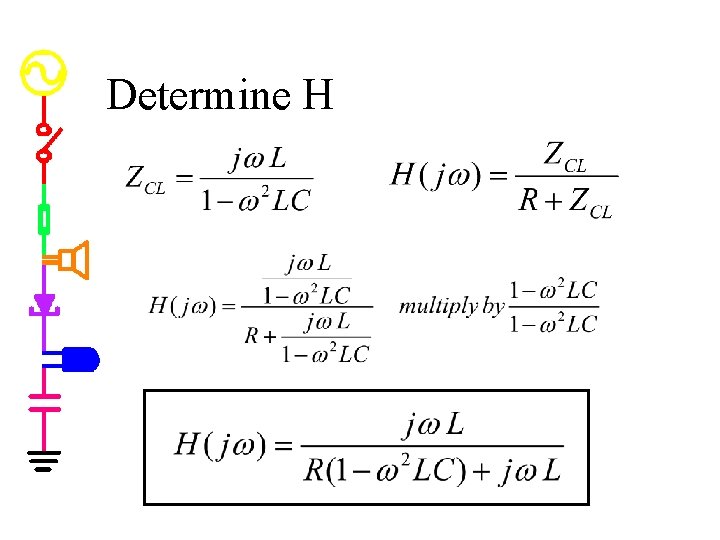
Determine H

At Very Low Frequencies At Very High Frequencies

At the Resonant Frequency

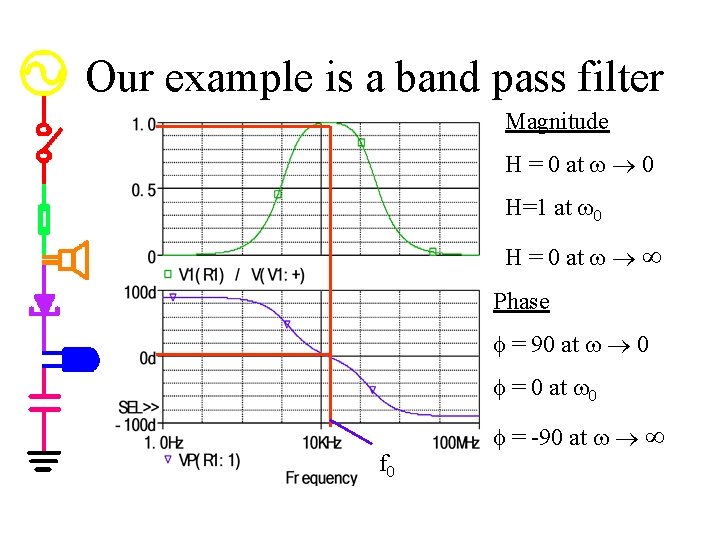
Our example is a band pass filter Magnitude H = 0 at w ® 0 H=1 at w 0 H = 0 at w ® ¥ Phase f = 90 at w ® 0 f = 0 at w 0 f = -90 at w ® ¥
 Instrumentation amplifier experiment
Instrumentation amplifier experiment Electronic instrumentation rpi
Electronic instrumentation rpi Rpi electronic instrumentation
Rpi electronic instrumentation Stepper motor full step sequence
Stepper motor full step sequence Is the electronic exchange of money or scrip
Is the electronic exchange of money or scrip Electronic field production
Electronic field production Part whole model subtraction
Part whole model subtraction Part to part ratio definition
Part to part ratio definition Part part whole
Part part whole What is a technical description?
What is a technical description? Function of under bar
Function of under bar The part of a shadow surrounding the darkest part
The part of a shadow surrounding the darkest part Two way anova minitab 17
Two way anova minitab 17 Schlosshotel weikersdorf
Schlosshotel weikersdorf Process instrumentation in project management
Process instrumentation in project management Health concerns
Health concerns Pfd boiler
Pfd boiler Process control instrumentation technology
Process control instrumentation technology General principles of instrumentation
General principles of instrumentation Gas turbine controls
Gas turbine controls Measurement and instrumentation ppt
Measurement and instrumentation ppt Pin instrumentation
Pin instrumentation P&id notation
P&id notation Power supply for nim instrumentation
Power supply for nim instrumentation Near infrared spectroscopy instrumentation
Near infrared spectroscopy instrumentation Man instrument system block diagram
Man instrument system block diagram Layers of protection
Layers of protection Pen grasp
Pen grasp Threshold in instrumentation
Threshold in instrumentation Infrared spectroscopy
Infrared spectroscopy Transmitter in instrumentation
Transmitter in instrumentation Smart plant instrumentation
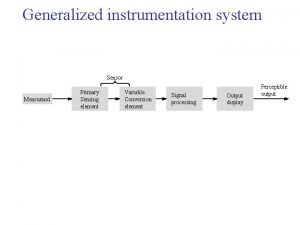
Smart plant instrumentation Generalized instrumentation system
Generalized instrumentation system Ir instrumentation
Ir instrumentation Emg instrumentation
Emg instrumentation Ee8403 measurements and instrumentation
Ee8403 measurements and instrumentation Power compensated dsc
Power compensated dsc What is data?
What is data? Chapter three research methodology
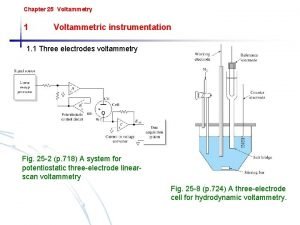
Chapter three research methodology Voltammetric instrumentation
Voltammetric instrumentation Basic concepts of measurement
Basic concepts of measurement Elements of generalized measurement system
Elements of generalized measurement system Instrumentation system
Instrumentation system Load cell amplifier circuit diagram
Load cell amplifier circuit diagram Turbine supervisory instrumentation
Turbine supervisory instrumentation Nicholas nethercote
Nicholas nethercote Special-purpose op-amp circuits
Special-purpose op-amp circuits Hydraulic structures ppt
Hydraulic structures ppt Characteristics of instrumentation amplifier
Characteristics of instrumentation amplifier Ir instrumentation
Ir instrumentation Hplc instrumentation diagram
Hplc instrumentation diagram Defense university research instrumentation program
Defense university research instrumentation program Pid diagram
Pid diagram Piping and instrumentation diagram (p&id)
Piping and instrumentation diagram (p&id) Electronique instrumentation
Electronique instrumentation Electronique instrumentation
Electronique instrumentation Instrumentation of centrifugation
Instrumentation of centrifugation Ngt the talk chapter 6
Ngt the talk chapter 6 Band pass filtering in biomedical instrumentation
Band pass filtering in biomedical instrumentation Flame photometry instrumentation
Flame photometry instrumentation Affinity chromatography instrumentation
Affinity chromatography instrumentation Electronique instrumentation
Electronique instrumentation