ECONOMETRIE II Chapitre 1 Multi colinarit et slection

ECONOMETRIE II

Chapitre 1 : Multi colinéarité et sélection du modèle optimal

I- Corrélation partielle Exemple : Un marchand de glaces, situé près de la tour Eiffel, cherche à calculer le coefficient de corrélation entre ses ventes ( ) et le nombre de touristes visitant ce monument ( ). Ces deux variables sont influencées par le climat : -Consommation des glaces est plus importante lorsqu’il fait chaud. -Les touristes hésitent à visiter un monument extérieur en cas de froid ou de pluie. -On appelle ( ) cette variable climatique.

I- Corrélation partielle Coefficient de corrélation partielle : Le coefficient de corrélation partielle mesure la liaison entre deux variables lorsque l’influence d’une troisième variable est retirée. = Coefficient de corrélation entre et = Coefficient de corrélation partielle entre l’influence de étant retirée et ,

I- Corrélation partielle Généralisation de la notion corrélation partielle : de corrélation partielle mesure la liaison entre deux Le coefficient variables lorsque l’influence d’une ou des autres variables explicatives est retirée. Soit y une variable à expliquer, et explicatives. 6 Coefficients de premier ordre : , et des variables 3 Coefficients de deuxième ordre : Plus le coefficient de corrélation partielle d’une variable est élevé, plus la contribution de cette variable est importante à l’explication globale du modèle.

I- Corrélation partielle Calcul du coefficient de corrélation partielle : Méthode 1: Du coefficient de corrélation simple -Entre le résidu de la régression de la variable à expliquer sur le sous ensemble des k-1 autres variables explicatives. - et le résidu de la régression de la variable explicative sur les k-1 variables explicatives. Exemple de calcul: Etape 1: = y–( + + Etape 2: = –( + + Etape 3: = ) )

I- Corrélation partielle Calcul du coefficient de corrélation partielle : Méthode 2: Du t de Student Dans un modèle à k variables explicatives, il existe une relation entre le coefficient de corrélation partielle et le t de Student : = + (n – k – 1) Cas particulier : Relation entre trois variables = -( (1 – )( ) – (1 ) )

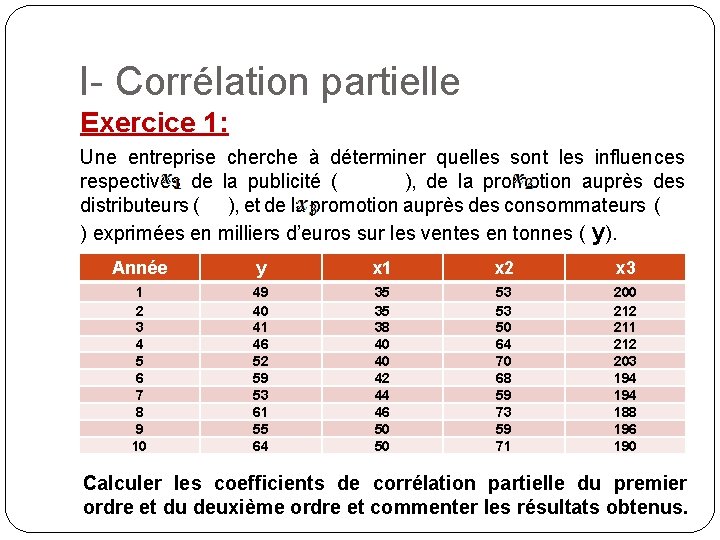
I- Corrélation partielle Exercice 1: Une entreprise cherche à déterminer quelles sont les influences respectives de la publicité ( ), de la promotion auprès des distributeurs ( ), et de la promotion auprès des consommateurs ( ) exprimées en milliers d’euros sur les ventes en tonnes ( y). Année y x 1 x 2 x 3 1 2 3 4 5 6 7 8 9 10 49 40 41 46 52 59 53 61 55 64 35 35 38 40 40 42 44 46 50 50 53 53 50 64 70 68 59 73 59 71 200 212 211 212 203 194 188 196 190 Calculer les coefficients de corrélation partielle du premier ordre et du deuxième ordre et commenter les résultats obtenus.

I- Corrélation partielle Relation entre coefficients de corrélation simple, partielle et multiple: 1– = (1 - ) = Coefficient de détermination de la régression de y sur x 1 et x 2 = Proportion du résidu expliqué par la variable x 2 seule. = Coefficient de détermination de la régression de y sur x 1

I- Corrélation partielle Exercice 2: Un économiste estime un modèle à trois variables explicatives : = 348. 4 + 56. 3 (4. 5) (8. 3) R² = n = (. ) = - 9. 5 (2. 1) + 234. 8 (4. 6) 0. 76 65 t de Student Le coefficient de corrélation linéaire entre y et x 1 est connu : = 0. 52 Calculer le coefficient de corrélation partielle

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 1 - Test de Klein Le test de Klein est fondé sur la comparaison du coefficient de détermination calculé sur le modèle à k variables et les coefficients de corrélation simple entre les variables explicatives pour i ≠ j. Si < Il y a présomption de multicoliéarité

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 1 - Test de Klein Le test de Klein est fondé sur la comparaison du coefficient de détermination calculé sur le modèle à k variables et les coefficients de corrélation simple entre les variables explicatives pour i ≠ j. Si < Il y a présomption de multicoliéarité

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 2 - Test de Farrar et Glauber La première étape consiste à calculer le déterminant de la matrice des coefficients de corrélation entre les variables explicatives. D= Lorsque la valeur du déterminant D tend vers zéro, le risque de multicolinéarité est important

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 2 - Test de Farrar et Glauber Exemple 1 : deux variables explicatives parfaitement corrélées. D= = = 0

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 2 - Test de Farrar et Glauber Exemple 2 : deux variables explicatives non corrélées. D= = = 1

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 2 - Test de Farrar et Glauber La deuxième étape consiste à effectuer un test x² selon les hypothèses suivantes : H 0 : D = 1 (les séries sont orthogonales) H 1 : D < 1 (les séries sont dépendantes) La valeur empirique du *x² calculée à partir de l’échantillon : * ²= x n = taille de l’échantillon K = k+1 nombre de variables explicatives (terme constant inclus) Ln = logarithme népérien

II- Tests de détection de multicolinéarité Test de détection d’une multicoliéarité: 2 - Test de Farrar et Glauber Règle de décision : x Si * ² ≥ dans la table à (K/2)(K-1) degrés de liberté et au x²Lu seuil L’hypothèse H 0 est rejeté, il y a donc présomption de multicolinéarité x Si * ² < x² Nous acceptons l’hypothèse d’orthogonalité

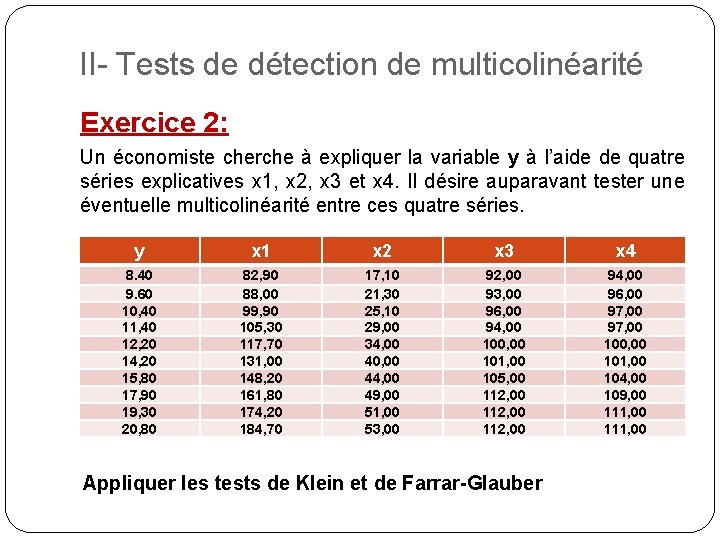
II- Tests de détection de multicolinéarité Exercice 2: Un économiste cherche à expliquer la variable y à l’aide de quatre séries explicatives x 1, x 2, x 3 et x 4. Il désire auparavant tester une éventuelle multicolinéarité entre ces quatre séries. y x 1 x 2 x 3 x 4 8. 40 9. 60 10, 40 11, 40 12, 20 14, 20 15, 80 17, 90 19, 30 20, 80 82, 90 88, 00 99, 90 105, 30 117, 70 131, 00 148, 20 161, 80 174, 20 184, 70 17, 10 21, 30 25, 10 29, 00 34, 00 40, 00 44, 00 49, 00 51, 00 53, 00 92, 00 93, 00 96, 00 94, 00 100, 00 101, 00 105, 00 112, 00 94, 00 96, 00 97, 00 100, 00 101, 00 104, 00 109, 00 111, 00 Appliquer les tests de Klein et de Farrar-Glauber

II- Tests de détection de multicolinéarité Comment remédier à la multicolinéarité ? Augmenter la taille de l’échantillon : Cette technique n’est pas efficace que si l’ajout d’observations diffère significativement de celles figurant déjà dans le modèle. La « Ridge Regression » : est une réponse purement numérique, il s’agit de transformer la matrice X’X en (X’X + c. I).

III- Choix du modèle optimal Sélection du modèle optimal Dans la pratique, l’économètre est souvent confronté aux choix de plusieurs variables explicatives x 1, x 2, …, xk candidates pour expliquer la variable y. Des procédures statistiques permettent de déterminer quelles variables retirer ou quelles variables ajouter dans un modèle. Cette démarche exclut tout raisonnement économique car elle permet d’aboutir à des modèles économétriques qui sont souvent bons sur le plan statistique mais dont l’interprétation économique s’avère nulle. Ces techniques de sélection de variables explicatives sont donc à manier avec prudence.

III- Choix du modèle optimal Sélection du modèle optimal Au problème de la sélection des variables explicatives s’joute celui du choix à effectuer entre plusieurs modèles concurrents, c’est-à-dire des modèles dont les variables sont toutes significatives mais qui ne sont pas les mêmes. La question se pose alors de sélectionner le meilleur modèle.

III- Choix du modèle optimal Sélection du modèle optimal Le critère de maximisation du R² (coefficient de détermination) consiste à retenir le modèle dont le R² est le plus élevé. Ce critère présente l’inconvénient de ne pas arbitrer entre la perte de degrés de liberté du modèle et l’ajustement qui en résulte. C’est pourquoi on préfère utiliser les critères de AKAIKE ou SCHWARZ afin de comparer des modèles impliquant un nombre différents de variables explicatives.

III- Choix du modèle optimal Sélection du modèle optimal Nous retenons le modèle qui minimise la fonction de Akaike (Akaike Information Criterion) : AIC = Ln (SCR/n) + 2 k/n Schwarz (Schwarz Criterion) : SC = Ln (SCR/n) + k. Ln(n)/n

III- Choix du modèle optimal Sélection du modèle optimal Avec : Ln = Logarithme népérien. SCR = Somme des carrés des résidus du modèle. n = nombre d’observations. k = nombre de variables explicatives. Nous allons examiner cinq méthodes qui vont nous permettre de retenir le meilleur modèle, celui qui est composé des variables qui sont : - Les plus corrélées avec la variable à expliquer. - Les moins corrélés entre elles.

III- Choix du modèle optimal Sélection du modèle optimal Toutes les régressions possibles Il s’agit de la méthode la plus simple dans son exposé : nous estimons toutes les combinaisons de régressions possibles ( possibilités, k = nombre de variables explicatives candidates). Le modèle retenu est celui dont le critère de Akaike ou de Schwartz est minimum pour un modèle comportant des variables explicatives toutes significatives. La limite d’utilisation de cette méthode est liée au nombre initial de variables explicatives candidates, par exemple si k=10, le nombre de combinaisons possibles est de 1023.

III- Choix du modèle optimal Sélection du modèle optimal L’élimination progressive ( « Backward Elimination » ) Cette procédure consiste, sur le modèle complet à k variables explicatives, à éliminer de proche en proche (c’est-à-dire en réestimant l’équation après chaque élimination) les variables explicatives dont les t de Student sont en dessous du seuil critique. Cette procédure n’est utilisable que si la première équation peut être effectivement estimée, ce qui n’est pas toujours le cas. En effet, lorsque le modèle comporte un nombre important de variables explicatives, le risque de colinéarité entre ces variables est élevé et la matrice X’X peut être singulière.

III- Choix du modèle optimal Sélection du modèle optimal La sélection progressive ( « Forward Regression» ) Dans cette procédure, on sélectionne, dans une première étape, la variable explicative dont le coefficient de corrélation simple est le plus élevé avec la variable y, soit xi cette variable. La deuxième étape consiste alors à calculer les coefficients de corrélation partielle r²yxj. xi pour j≠i et à retenir la variable explicative ayant le coefficient le plus élevé. La sélection s’arrête lorsque les t de Student des variables explicatives sont inférieurs au seuil critique.

III- Choix du modèle optimal Sélection du modèle optimal La régression pas à pas( « Stepwise Regression» ) Cette procédure est identique à la précédente, sauf qu’après avoir incorporé une nouvelle variable explicative, nous examinons les t de Student de chacune des variables explicatives préalablement sélectionnées et nous éliminons du modèle celle(s) dont le t du Student est inférieur au seuil critique.

III- Choix du modèle optimal Sélection du modèle optimal La régression par étage( « Stagewise Regression» ) C’est un processus de sélection de variables explicatives permettant de minimiser les inter corrélations entre les séries explicatives par étude du résidu. La première étape : La variable explicative dont le coefficient de corrélation simple est le plus élevé avec la variable y est sélectionnée, soit xi cette variable. La deuxième étape : Calcul du résidu de la régression de y sur xi: = y–( + ) Les coefficients de corrélation simple entre le résidu e 1 et les variables explicatives sont calculés, nous retenons la variable explicative dont le coefficient est le plus élevé. Soit xj cette variable explicative.

III- Choix du modèle optimal Sélection du modèle optimal La troisième étape : Nous calculons un nouveau résidu: = y–( + + ) Les coefficients de corrélation simple entre le résidu e 2 et les variables explicatives sont calculés, nous retenons la variables explicatives dont le coefficient est le plus élevé, e qui permet de dégager un nouveau résidu. La procédure est arrêtée lorsque les coefficients de corrélation ne sont plus significativement différents de 0.

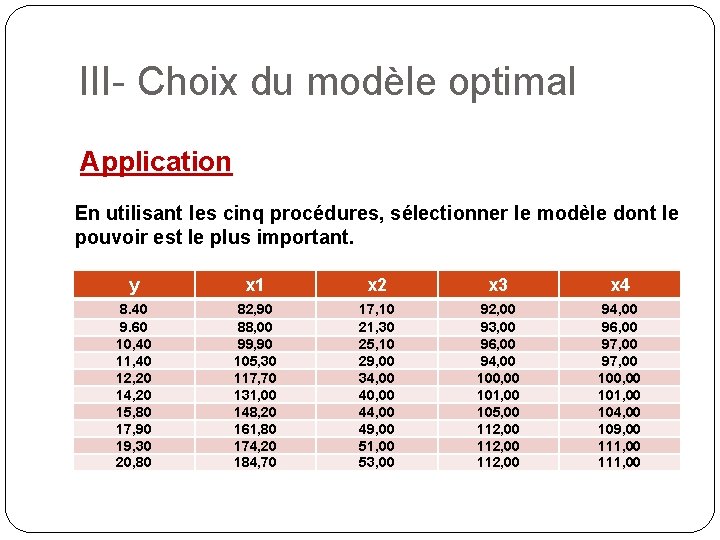
III- Choix du modèle optimal Application En utilisant les cinq procédures, sélectionner le modèle dont le pouvoir est le plus important. y x 1 x 2 x 3 x 4 8. 40 9. 60 10, 40 11, 40 12, 20 14, 20 15, 80 17, 90 19, 30 20, 80 82, 90 88, 00 99, 90 105, 30 117, 70 131, 00 148, 20 161, 80 174, 20 184, 70 17, 10 21, 30 25, 10 29, 00 34, 00 40, 00 44, 00 49, 00 51, 00 53, 00 92, 00 93, 00 96, 00 94, 00 100, 00 101, 00 105, 00 112, 00 94, 00 96, 00 97, 00 100, 00 101, 00 104, 00 109, 00 111, 00

III- Choix du modèle optimal Eviews Calcul d’un coefficient de corrélation partielle Exemple de calcul de r²yx 3. x 1 x 2 LS Y C X 1 X 2 GENR E 1 = RESID LS X 3 C X 1 X 2 GENR E 2 = RESID scalar rau = @cor(E 1, E 2)

III- Choix du modèle optimal Eviews Test de Klein Programme scalar test 1 = 0 ‘test un indicateur de colinéarité égal à 1 en cas de risque equation eqt. ls y c x 1 x 2 x 3 x 4 scalar cr = @r 2 for !i = 1 to 4 for !j = 1 to 4 if !i <> !j then scalar cp!i!j = @cor(x!i, x!j)^2 if cp!i!j > cr then test 1 = 1 endif next

III- Choix du modèle optimal Eviews Test de Farrar et Glauber Programme ls y c x 1 x 2 x 3 x 4 matrix(4, 4) mar for !i = 1 to 4 for !j = 1 to 4 mar(!i, !j) = @cor(x!i, x!j) next scalar dt = @det(mar) scalar chie = -(@regobs-1 -(2*@ncoef+5)/6)*log(dt) scalar ndf = 0. 5*@ncoef*(@ncoef-1) if @chisq(chie, ndf) < 0. 05 then scalar test 2 = 0 else scalar test 2 = 1 Endif Si le test 2 = 1, on rejette H 0, il y a présomption de multicolinéarité.

III- Choix du modèle optimal Eviews Toutes les régressions possibles !a = 1 FOR !I =1 TO 4 equation eq!a. ls Y C X!i !a = !a + 1 next FOR !I = 1 TO 3 FOR !J = !I+1 TO 4 equation eq!a. ls Y C X!I X!J 'equation à deux variables !a = !a + 1 next FOR !I = 1 TO 2 FOR !J = !I+1 TO 3 FOR !K = !J+1 TO 4 equation eq!a. ls Y C X!I X!J X!K 'equation à trois variables !a = !a + 1 next

III- Choix du modèle optimal Eviews equation eq!a. ls Y C X 1 X 2 X 3 X 4 Scalar BEST = 0 FOR !I = 1 TO 15 scalar IND = 0 scalar NV = eq!I. @ncoef for !J = 2 TO NV scalar te =@abs( eq!I. C(!J)/sqr(eq!I. @covariance(!J, !J))) scalar ddl = eq!I. @regobs- eq!I. @ncoef IF @tdist(te, ddl)> 0. 05 then ind = 1 endif NEXT !J IF IND = 0 then IF eq!I. @R 2 > BEST then scalar neq= !I BEST = eq!I. @R 2 ENDIF NEXT

III- Choix du modèle optimal Eviews Parmi ces 15 équation, laquelle est la meilleure? ? -Il faut éliminer celles dont un ou plusieurs ratios de Student ( sauf le terme constant) sont inférieurs au seuil critique (environ 2. 30) : M 5, M 6, M 7, M 8, M 10, M 11, M 12, M 14, M 15). - Parmi le reste des équations, on sélectionne celle dont le critère de Akaike et de Schwarz est le plus faible, d’où M 13

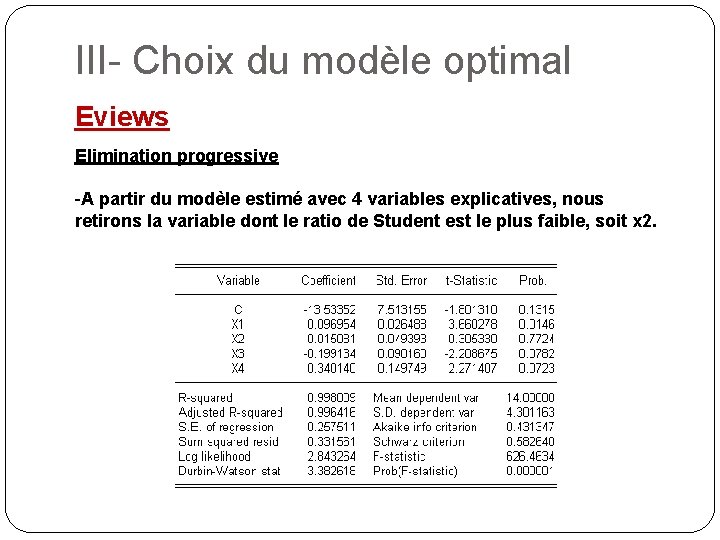
III- Choix du modèle optimal Eviews Elimination progressive -A partir du modèle estimé avec 4 variables explicatives, nous retirons la variable dont le ratio de Student est le plus faible, soit x 2.

III- Choix du modèle optimal Eviews Elimination progressive -Le modèle estimé est le modèle 13, toutes les variables sont significatives (t* > 2. 30), la procédure de sélection s’arrête:

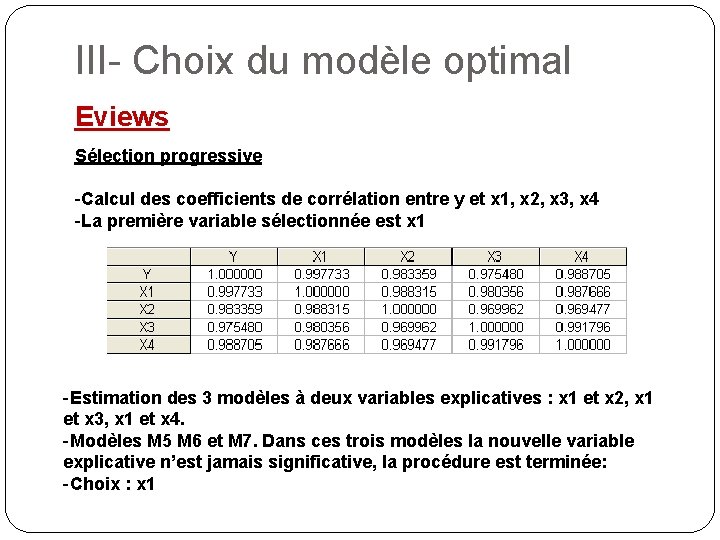
III- Choix du modèle optimal Eviews Sélection progressive -Calcul des coefficients de corrélation entre y et x 1, x 2, x 3, x 4 -La première variable sélectionnée est x 1 -Estimation des 3 modèles à deux variables explicatives : x 1 et x 2, x 1 et x 3, x 1 et x 4. -Modèles M 5 M 6 et M 7. Dans ces trois modèles la nouvelle variable explicative n’est jamais significative, la procédure est terminée: -Choix : x 1