ECE 700 07 Game Theory with Engineering Applications
































- Slides: 35

ECE 700. 07: Game Theory with Engineering Applications Lecture 7: Games with Incomplete Information Seyed Majid Zahedi

Outline • Bayesian games • Bayes-Nash equilibrium • Auctions • Readings: • MAS Sec. 6. 3, GT Sec. 6. 1 - 6. 5

Bayesian Games: Games of Incomplete Information • So far, we assumed all agents know what game they are playing • Number of agents • Actions available to each agent • Utilities associated with each outcome • In extensive form games, actions may not be common knowledge, but game itself is • Bayesian games allow us to represent agents’ uncertainties about game being played • Uncertainty is represented as commonly known probability distribution over possible games • We make following assumptions • All games have same number of agents and same strategy space for each agents • Possible games only differ in agents’ utilities for each outcome

Example: Bayesian Entry Deterrence Game • Entran t Incumbent Enter Stay Out Build (0, -1) (2, 0) Build (3, -1) (5, 0) Don’t Build (2, 1) (3, 0) High Building Cost Low Building Cost

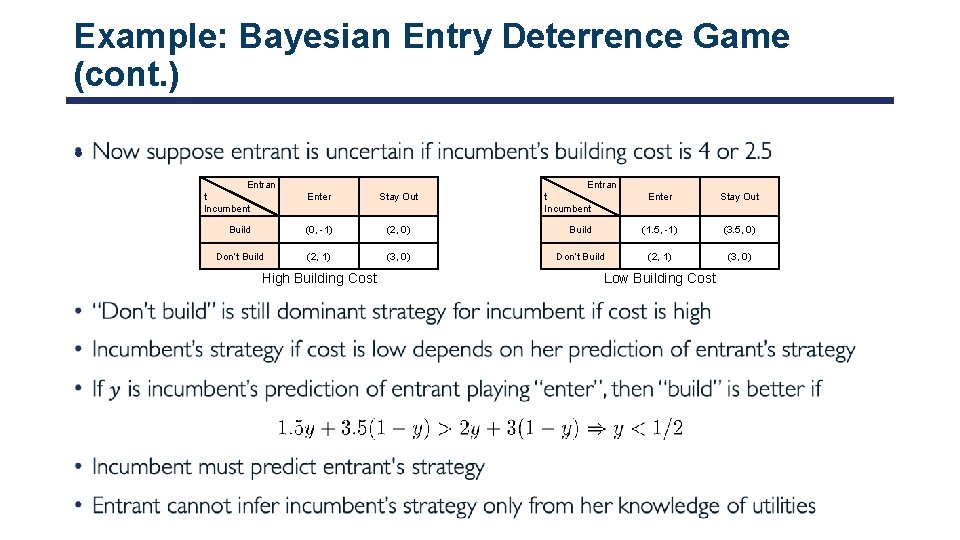
Example: Bayesian Entry Deterrence Game (cont. ) • Entran t Incumbent Enter Stay Out Build (0, -1) (2, 0) Build (1. 5, -1) (3. 5, 0) Don’t Build (2, 1) (3, 0) High Building Cost Low Building Cost

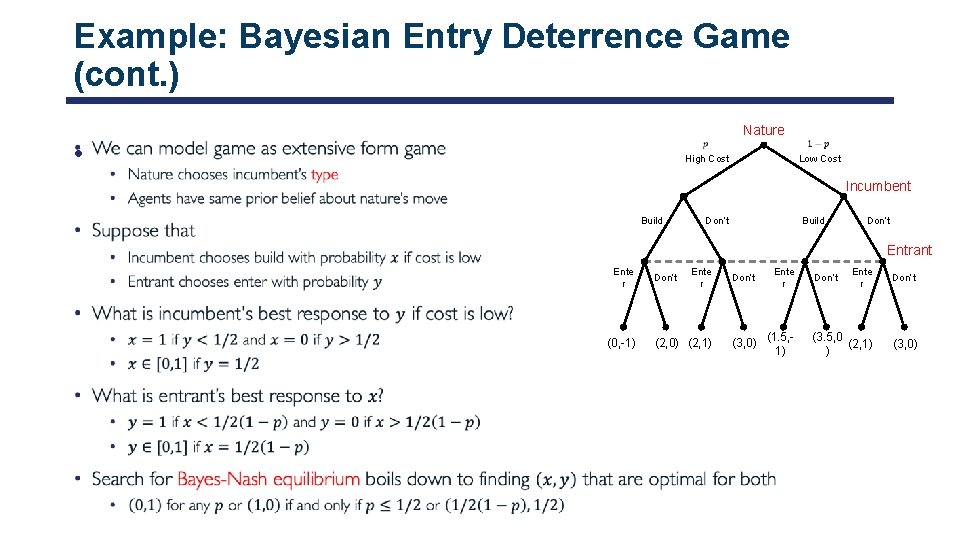
Example: Bayesian Entry Deterrence Game (cont. ) Nature • Low Cost High Cost Incumbent Build Don’t Entrant Ente r (0, -1) Ente r Don’t Ente r (2, 0) (2, 1) (3, 0) (1. 5, 1) Don’t Ente r Don’t (3. 5, 0 (2, 1) ) (3, 0) Don’t

Bayesian Games Model •

Expected Utilities • Ex-post expected utility • Ex-interim expected utility • Ex-ante expected utility

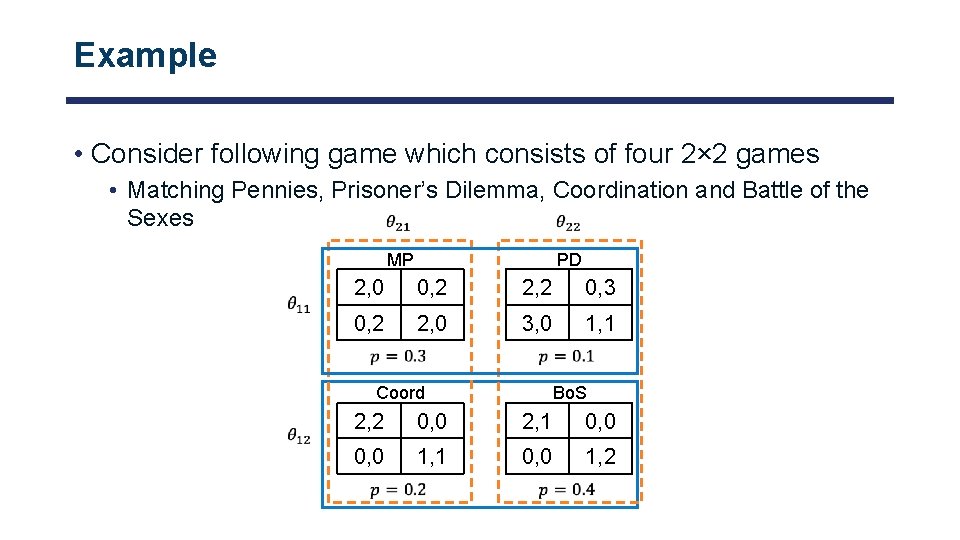
Example • Consider following game which consists of four 2× 2 games • Matching Pennies, Prisoner’s Dilemma, Coordination and Battle of the Sexes MP PD 2, 0 0, 2 2, 2 0, 3 0, 2 2, 0 3, 0 1, 1 Coord Bo. S 2, 2 0, 0 2, 1 0, 0 1, 2

Example (cont. ) •

Strategies •

Bayes-Nash Equilibrium •

Ex-Post Equilibrium •

Example: Incomplete Information Cournot •

Example: Incomplete Information Cournot (cont. ) •

Auctions • Major application of Bayesian games is in auctions • Auctions are commonly used to sell (allocate) items to bidders • Auctioneer often would like to maximize her revenue • Bidders’ valuations are usually unknown to others and auctioneer • Allocating items to bidders with highest valuations is often desirable • Extracting private valuations could be challenging • E. g. , giving painting for free to bidder with highest valuation would create incentive for all bidders to overstate their valuations

Different Auctions and Terminologies • English auction: ascending sequential bids • First price auction: bidders bid simultaneously, highest bid wins, winner pays her bid • Second price action: similar to first price, except that winner pays second highest bid • Dutch auction: descending sequential prices; price is reduced until one stops auction • Private valuations: valuation of each bidder is independent of others’

Modeling First and Second Price Auctions •

Second Price Auctions •

Truthful Bidding •

Expected Payment in Second Price Auctions •

First Price Auctions •

First Price Auctions (cont. ) •

Expected Payment in First Price Auctions •

Revenue Equivalence • In standard auctions item is sold to bidder with highest submitted bid • Suppose that values are i. i. d and all bidders are risk neutral • [Theorem] Any symmetric and increasing equilibria of any standard auction (such that expected payment of bidder with value zero is zero) yields same expected revenue to auctioneer

Common Value Auctions (Dependent Signals) •

Oil Field Example: Expected Value •

Oil Field Example: Second Price Auction and Truthful Bidding •

Winner’s Curse •

Common Value Auctions (Independent Signals) •

Oil Field Example II: Second Price Auction and Truthful Bidding •

Oil Field Example II: Second Price Auction and Truthful Bidding (cont. ) •

Oil Field Example II: First Price Auction • Analysis is similar to that of first price auctions with private values • It can be shown that unique symmetric BNE is for each bidder to bid • It can be shown that expected revenue is equal to first price auction • Revenue equivalence principle continues to hold for common values

Questions?

Acknowledgement • This lecture is a slightly modified version of one prepared by • Asu Ozdaglar [MIT 6. 254]
 Game theory with engineering applications
Game theory with engineering applications Pirate game sheet
Pirate game sheet Game lab game theory
Game lab game theory Liar game game theory
Liar game game theory Liar game game theory
Liar game game theory Principles of complex systems for systems engineering
Principles of complex systems for systems engineering Elegant systems
Elegant systems Game theory and graph theory
Game theory and graph theory Gis applications in civil engineering
Gis applications in civil engineering Genetic engineering applications
Genetic engineering applications Civil engineering applications of ground penetrating radar
Civil engineering applications of ground penetrating radar Testing conventional applications in software engineering
Testing conventional applications in software engineering Engineering optimization methods and applications
Engineering optimization methods and applications Engineering plastics applications
Engineering plastics applications Principles and applications of electrical engineering
Principles and applications of electrical engineering Allan
Allan Testing conventional applications in software engineering
Testing conventional applications in software engineering Grabber
Grabber Farming game rules pdf
Farming game rules pdf A formal approach to game design and game research
A formal approach to game design and game research Image sets
Image sets Spectral graph theory and its applications
Spectral graph theory and its applications A brief introduction to spectral graph theory
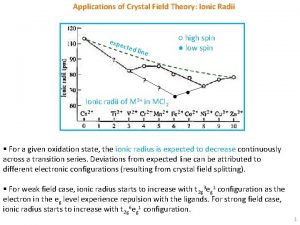
A brief introduction to spectral graph theory Crystal field effect on ionic radii
Crystal field effect on ionic radii Managerial economics: theory, applications, and cases
Managerial economics: theory, applications, and cases Computer based system engineering in software engineering
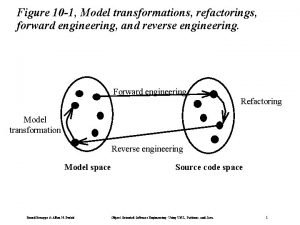
Computer based system engineering in software engineering Forward engineering and reverse engineering
Forward engineering and reverse engineering Forward and reverse engineering
Forward and reverse engineering Www.vdab.be
Www.vdab.be Tt ab-700 ultra glide
Tt ab-700 ultra glide Tt ab-700 ultra glide
Tt ab-700 ultra glide Tt-ab 700
Tt-ab 700 Trent 700 engine diagram
Trent 700 engine diagram 700 ad
700 ad Nbc ta 701
Nbc ta 701 Maz dump truck
Maz dump truck