MANAGERIAL ECONOMICS THEORY APPLICATIONS AND CASES W Bruce

MANAGERIAL ECONOMICS: THEORY, APPLICATIONS, AND CASES W. Bruce Allen | Neil A. Doherty | Keith Weigelt | Edwin Mansfield Chapter 4 ESTIMATING DEMAND FUNCTIONS

THE IDENTIFICATION PROBLEM • Task of estimating the demand curve • Difficult, since both demand supply curves are shifting over time • Shifts occur because nonprice variables are influencing demand supply

Objectives • To investigate regression analysis to estimate a product’s demand function • To discuss some of the important problems in regression analysis such as • Multicollinearity • Serial correlation

THE IDENTIFICATION PROBLEM (CONT’D) • Econometrics techniques such as regression attempt to estimate demand curves when both supply and demand are shifting • Unless all variables affecting the demand are included in the estimation, the true demand curve may be significantly different from the estimated one.

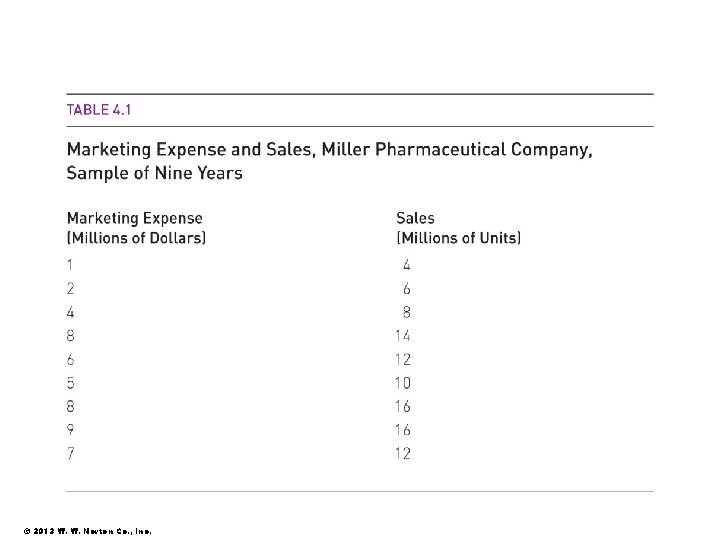
REGRESSION ANALYSIS • The study of the relationship between one variable called the explained or dependent variable and one or more other variables called independent or explanatory variables. • Example: relationship between the level of sales of a product and the advertising expenditures on that product. • Objective: Estimating a demand curve

REGRESSION ANALYSIS • Regression analysis derives an equation that can be used to estimate the unknown value of one variable on the basis of the known value of the other variable. • Objective: Estimating the unknown value of next year’s sales based on the data in the previous years and given the next year’s expenses.

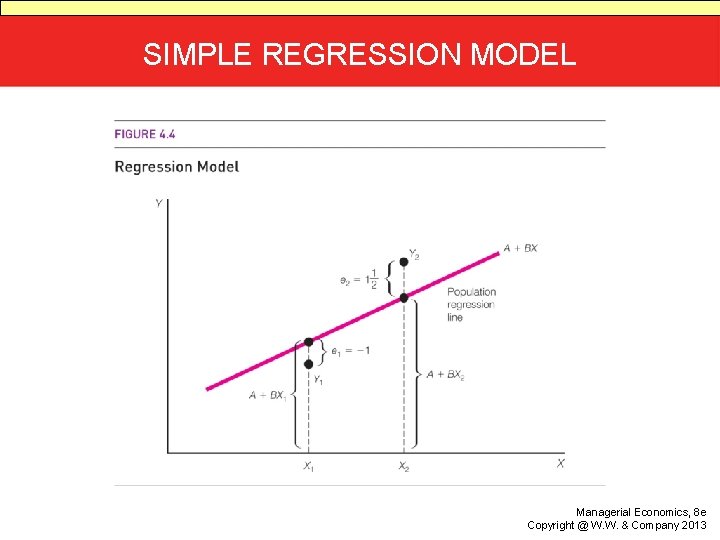
SIMPLE REGRESSION MODEL • Model: a simplified or idealized representation of reality • Assumption: the mean value of Y, given the value of X, is a linear function of X: • Yi = A + B(Xi) + ei • Line resulting from regressing the dependent variable on the independent variable where the entire population of values of the variables is used

SIMPLE REGRESSION MODEL (CONT’D) • Error term: a random amount that is added or subtracted from the population regression line • Assumptions about the error term are necessary in order to conduct regression analyses. • The values of the error terms are independent and have zero mean. • The error terms have the same variance.

SIMPLE REGRESSION MODEL Managerial Economics, 8 e Copyright @ W. W. & Company 2013

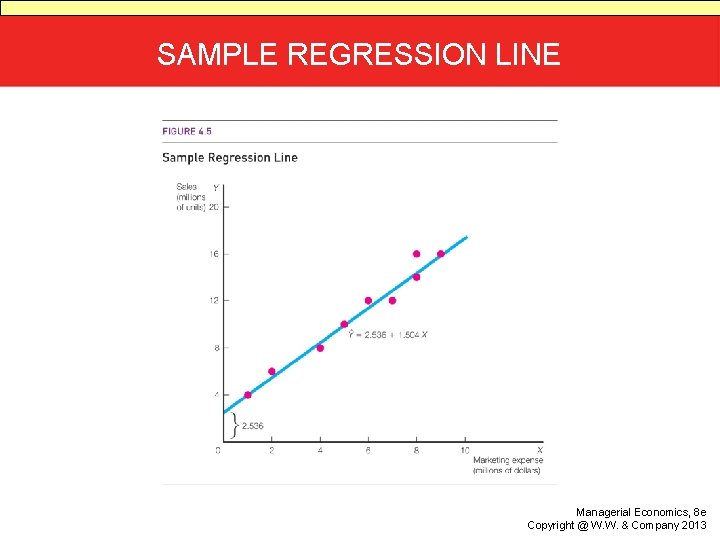
SAMPLE REGRESSION LINE • The goal is to obtain a mathematical equation for a line that describes the avarage relationship between the dependent and independent variables. • The goal is to obtain estimates of A and B, call them a and b • Estimated Regression Line or sample regression line is the line resulting from regressing the dependent variable on the independent variable where only a sample of the variables is used.

SAMPLE REGRESSION LINE (CONT’D) • General Expression is: • Y(hat) = a + b(X) • Y(hat) is the value of the dependent variable predicted by the regression line. • a and b are estimators of A and B, respectively, of the population regression line. • a measures the intercept of the regression line. • b measures its slope.

SAMPLE REGRESSION LINE (CONT’D) • a measures the value of the dependent variable when the independent variables have a value of zero. • b measures the change in the predicted value of Y, associated with a one-unit change in the value of X. • Method of Least Squares is often used to determine the values of a and b.

Method of Least Squares • Define residuals =observed– predicted. • Sum of squared residuals • Goal: To choose a and b to minimize the sum of squared residuals. The idea is to differentiate the above sum of squared residuals with respect to a and b and set the partial derivatives equal to 0.

SAMPLE REGRESSION LINE Managerial Economics, 8 e Copyright @ W. W. & Company 2013

COEFFICIENT OF DETERMINATION • A measure of how well the sample regression line fits the data • The coefficient of determination is denoted by R 2. • Its value lies between 0 and 1. The closer it is to 1, the better the fit; the closer to zero, the worse the fit. • In a simple linear regression, R 2 is the square of the correlation coefficient, r.

COEFFICIENT OF DETERMINATION Managerial Economics, 8 e Copyright @ W. W. & Company 2013

MULTIPLE REGRESSION • A multiple regression includes two or more independent variables, whereas a simple regression includes only one independent variable. • In the case of the Miller Pharmaceutical Company: • Y i = A + B 1 X i + B 2 P i + e i • As in the case of simple regression, least squares estimates are obtained.

SOFTWARE PACKAGES AND COMPUTER PRINTOUTS • Regression analyses are carried out on computers. • Some widely used packages are Minitab, SAS, SPSS, and in Microsoft Excel. • Packages produce similar output.

SOFTWARE PACKAGES AND COMPUTER PRINTOUTS Managerial Economics, 8 e Copyright @ W. W. & Company 2013

INTERPRETING THE OUTPUT OF STATISTICAL SOFTWARE • The Standard Error of the Estimate is a measure of the amount of scatter of individual observations around the regression line. • It is useful in constructing prediction intervals.

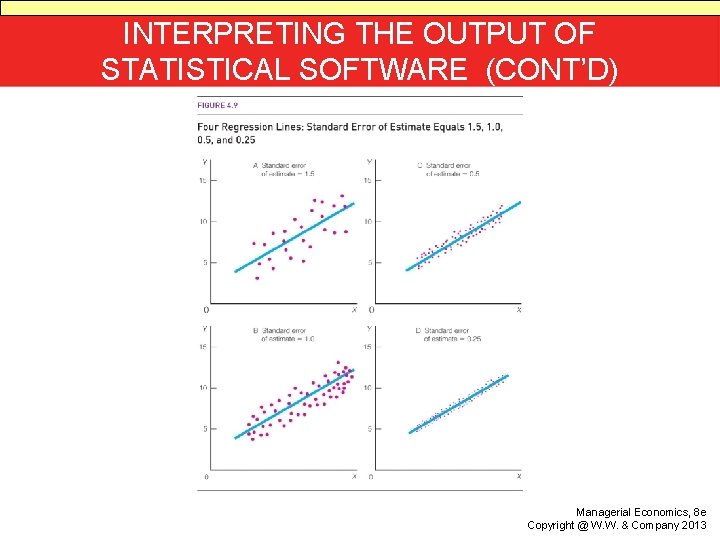
INTERPRETING THE OUTPUT OF STATISTICAL SOFTWARE (CONT’D) Managerial Economics, 8 e Copyright @ W. W. & Company 2013

ANALYZING OVERALL FIT: F STATISTIC • The F Statistic • Answers the question of whether any of the independent variables really influences the dependent variable • Large values of F tend to imply that at least one of the independent variables has an effect on the dependent variables.

ANALYZING OVERALL FIT: F STATISTIC (CONT’D) • Tables of the F distribution are used to determine the probability of the observed value of the F Statistic having arisen by chance alone, given that none of the independent variables has any effect on the dependent variable. • This probability is denoted by “p. ”

TESTING HYPOTHESIS ABOUT INDIVIDUAL REGRESSION COEFFICIENTS: t STATISTIC) • The t statistic. • Used to determine which of the independent variables influences the dependent variable. • Whether a particular independent variable influences the dependent variable • Test whether the true value of the parameter estimate is zero. • The higher the value of the t-statistic, the smaller the value of the regression coefficient is zero.

MULTICOLLINEARITY • A condition where two or more independent variables are very highly correlated • Impacts the accuracy of the coefficient estimates • Difficult to reduce the extent of multicollinearity

SERIAL CORRELATION • Violation of the assumption that the error terms are independent • Positive serial correlation occurs when the error terms in regression analyses have the same sign as in the previous time period. • Negative serial correlation occurs when the error terms have the opposite signs as in the previous time period.

SERIAL CORRELATION (CONT’D) • • Presence of serial correlation is tested by use of the Durbin-Watson statistic d. Reject hypothesis of no serial correlation against alternative hypothesis of positive serial correlation when d < d. L and accept when d > d. U. Values of d. L and d. U are shown in Appendix E, Table E. 7. Note that values of d. L and d. U depend on both sample size and the number of independent variables.

SERIAL CORRELATION (CONT’D) • One solution to deal with the problem of serial correlation is to take first differences of all the independent and dependent variables in the regression. • Note that the sample size is reduced.

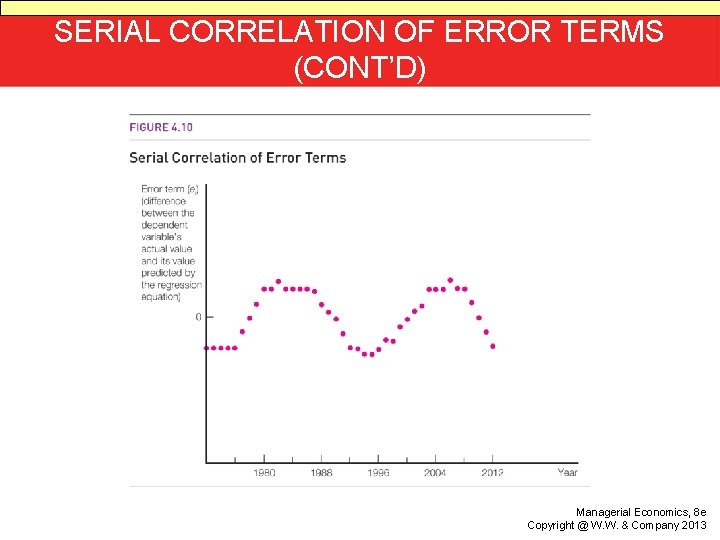
SERIAL CORRELATION OF ERROR TERMS (CONT’D) Managerial Economics, 8 e Copyright @ W. W. & Company 2013

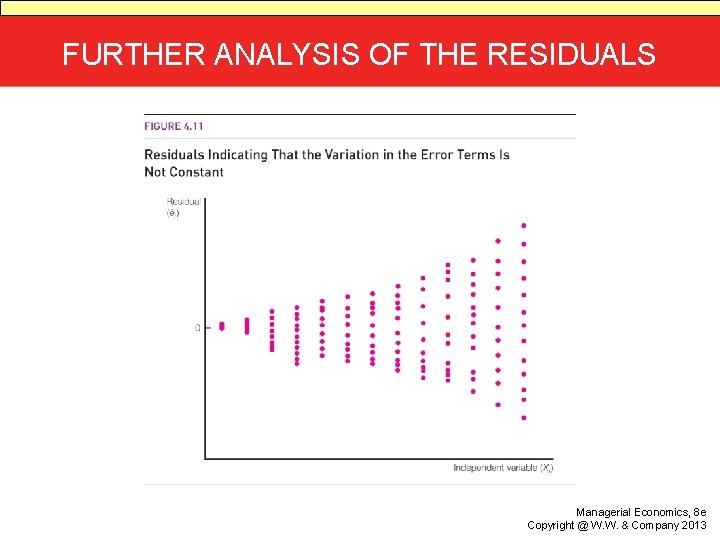
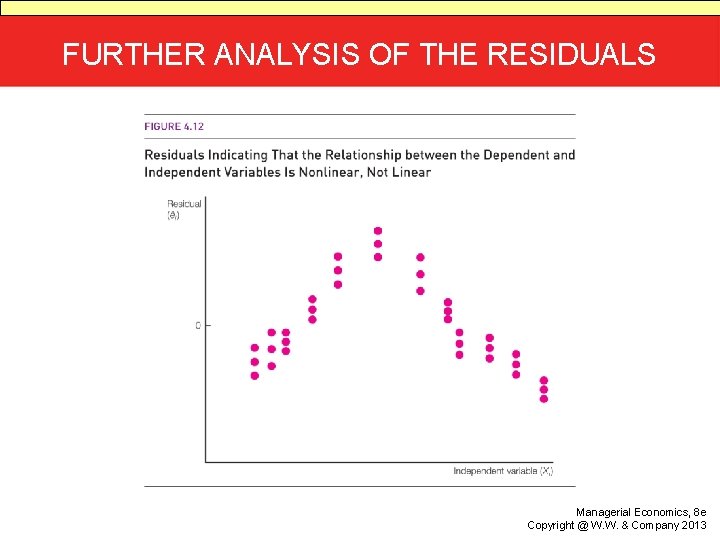
FURTHER ANALYSIS OF THE RESIDUALS Managerial Economics, 8 e Copyright @ W. W. & Company 2013

Examples 1. The Klein Corporation’s marketing department, using regression analysis, estimates the firm’s demand function, the result being Q= -104 - 2. 1 P + 3. 2 I+ 1. 5 A + 1. 6 Z R 2= 0. 89 Standard error of estimate=108 where Q is the quantity demanded of the firm’s product (in tons), P is the price of the firm’s product (in dollars per ton), I is per capita income (in dollars), A is the firm’s advertising expenditure (in thousands of dollars), and Z is the price (in dollars) of a competing product. The regression is based on 200 observations. a) According to the statistical software, the probability is 0. 005 that the t statistic for the regression coefficient of A would be as large (in absolute terms) as it is in this case if in fact A has no effect on Q. Interpret this result.

Examples b. If I =5, 000, A = 20, and Z= 1, 000, what is the Klein Corporation’s demand curve? c. If P= 500 (and the conditions in part b hold), estimate the quantity demanded of the Klein Corporation’s product. d. How well does this regression equation fit the data? 2) Since all the Hawkins Company’s costs (other than advertising) are essentially fixed costs, it wants to maximize its total revenue (net of advertising expenses). According to a regression analysis (based on 124 observations) carried out by a consultant hired by the Hawkins Company, Q = -23 - 4. 1 P+ 4. 2 I + 3. 1 A

Examples • where Q is the quantity demanded of the firm’s product (in dozens), P is the price of the firm’s product (in dollars per dozen), I is per capita income (in dollars), and A is advertising expenditure (in dollars). a. If the price of the product is $10 per dozen, should the firm increase its advertising? b. If the advertising bud get is fixed at $10, 000 and per capita income equals $8, 000, what is the firm’s marginal revenue curve? c. If the advertising bud get is fixed at $10, 000 and per capita income equals $8, 000, what price should managers charge?

Examples 3. The 2012 sales and profits of seven clothes companies were as follows: Sales ($ billions) Profit ($ billions) Maxx 5. 7 0. 27 Bleu 6. 7 0. 12 Goden 0. 2 0. 00 Triex 0. 6 0. 04 Chateau 3. 8 0. 05 L&T 12. 5 0. 46 Eastview 0. 5 0. 00 Firm

Examples a. Calculate the sample regression line, where profit is the dependent variable and sales is the independent variable. b. Estimate the 2012 average profit of a clothing firm with 2012 sales of $0. 2 billion. c. Can this regression line be used to predict a clothing firm’s profit in 2026? Explain.