ECE 700 07 Game Theory with Engineering Applications

ECE 700. 07: Game Theory with Engineering Applications Lecture 3: Games in Normal Form Seyed Majid Zahedi

Outline • Strategic form games • Dominant strategy equilibrium • Pure and mixed Nash equilibrium • Iterative elimination of strictly dominated strategies • Price of anarchy • Correlated equilibrium • Readings: • MAS Sec. 3. 2 and 3. 4, GT Sec. 1 and 2

Strategic Form Games •

Example: Prisoner’s Dilemma • Prisoner 2 Prisoner 1 Stay Silent Confess Stay Silent (-1, -1) (-3, 0) Confess (0, -3) (-2, -2)

Strategies • Strategy is complete description of how to play • It requires full contingent planning • As if you have to delegate play to “computer” • You would have to spell out how game should be played in every contingency • In chess, for example, this would be an impossible task • In strategic form games, there is no difference between action and strategy (we will use them interchangeably)

Finite Strategy Spaces • Agent 2 Agent 1 Heads Tails Heads (-1, 1) (1, -1) Tails (1, -1) (0, 0)

Infinite Strategy Spaces •

Dominant Strategy • Prisoner 2 Prisoner 1 Stay Silent Confess Stay Silent (-1, -1) (-3, 0) Confess (0, -3) (-2, -2)

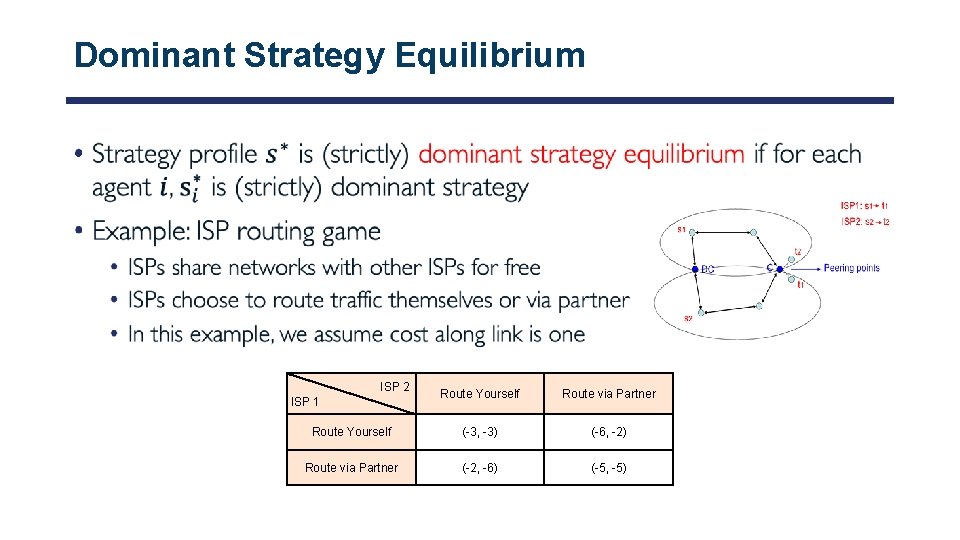
Dominant Strategy Equilibrium • ISP 2 ISP 1 Route Yourself Route via Partner Route Yourself (-3, -3) (-6, -2) Route via Partner (-2, -6) (-5, -5)

Dominated Strategies •

Rationality and Strictly Dominated Strategies Prisoner 2 Prisoner 1 Stay Silent Confess Suicide Stay Silent (-1, -1) (-3, 0) (0, -10) Confess (0, -3) (-2, -2) (-1, -10) Suicide (-10, 0) (-10, -10) • There is no DS because of additional “suicide” strategy • Strictly dominated strategy for both prisoners • No “rational” agent would choose “suicide” • No agent should play strictly dominated strategy

Rationality and Strictly Dominated Strategies (cont. ) • If A 1 knows that A 2 is rational, then she can eliminate A 2’s “suicide” strategy, and likewise for A 2 • After one round of elimination of strictly dominated strategies, we are back to prisoner’s dilemma game • Iterated elimination of strictly dominated strategies leads to unique outcome, “confess, confess” • Game is dominance solvable (We will come back to this later)

How Reasonable is Dominance Solvability? • Consider k-beauty contest game is dominance solvable! 100 dominated (2/3)*100 … 0 dominated after removal of (originally) dominated strategies

Existence of Dominant Strategy Equilibrium • Does matching pennies game have DSE? Agent 2 Agent 1 Heads Tails Heads (-1, 1) (1, -1) Tails (1, -1) (-1, 1) • Dominant strategy equilibria do not always exist

Best Response •

Pure Strategy Nash Equilibrium •

Example: Battle of the Sexes Wife Husband Football Opera Football (4, 1) (-1, -1) Opera (-1, -1) (1, 4) • Couple agreed to meet this evening • They cannot recall if they will be attending opera or football • Husband prefers football, wife prefers opera • Both prefer to go to same place rather than different ones

Existence of Pure Strategy Nash Equilibrium • Does matching pennies game have pure strategy NE? Agent 2 Agent 1 Heads Tails Heads (-1, 1) (1, -1) Tails (1, -1) (-1, 1) • Pure strategy Nash equilibria do not always exist

Mixed Strategies •

Strict Dominance by Mixed Strategy • Agent 2 Agent 1 a b a (2, 0) (-1, 0) b (0, 0) c (-1, 0) (2, 0)

Iterative Elimination of Strictly Dominated Strategies •

Mixed Strategy Nash Equilibrium •

Mixed Strategy Nash Equilibria (cont. ) •

Finding Mixed Strategy Nash Equilibrium • Wife Husband Football Opera Football (4, 1) (-1, -1) Opera (-1, -1) (1, 4)

Example: Bertrand Competition with Capacity Constraints •

Example: Bertrand Competition with Capacity Constraints (cont. ) •

Example: Bertrand Competition with Capacity Constraints (cont. ) •

Example: Bertrand Competition with Capacity Constraints (cont. ) •

Nash’s Theorem • Theorem (Nash): Every finite game has mixed strategy NE • Why is this important? • Without knowing the existence of equilibrium, it is difficult (perhaps meaningless) to try to understand its properties • Armed with this theorem, we also know that every finite game has at least one equilibrium, and thus we can simply try to locate equilibria • Knowing that there might be multiple equilibria, we should study efficiency/inefficiency of games’ equilibria

Example: Braess’s Paradox • T. Roughgarden, Lectures Notes on Algorithmic Game Theory

Example: Braess’s Paradox (cont. ) •

Correlated Strategies • Wife Husband Football Opera Football (4, 1) (-1, -1) Opera (-1, -1) (1, 4)

Correlated Strategies (cont. ) •

Correlated Equilibrium •

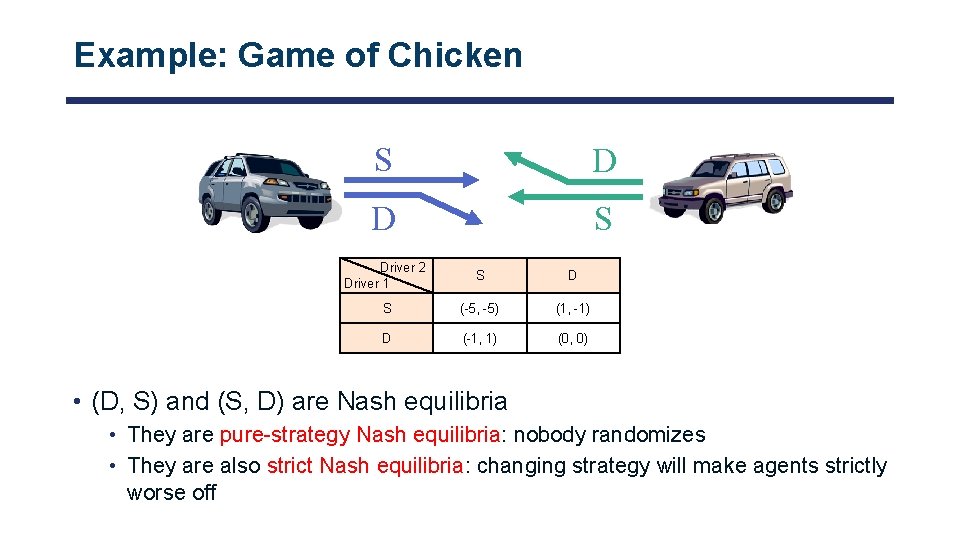
Example: Game of Chicken S D D S Driver 2 Driver 1 S D S (-5, -5) (1, -1) D (-1, 1) (0, 0) • (D, S) and (S, D) are Nash equilibria • They are pure-strategy Nash equilibria: nobody randomizes • They are also strict Nash equilibria: changing strategy will make agents strictly worse off

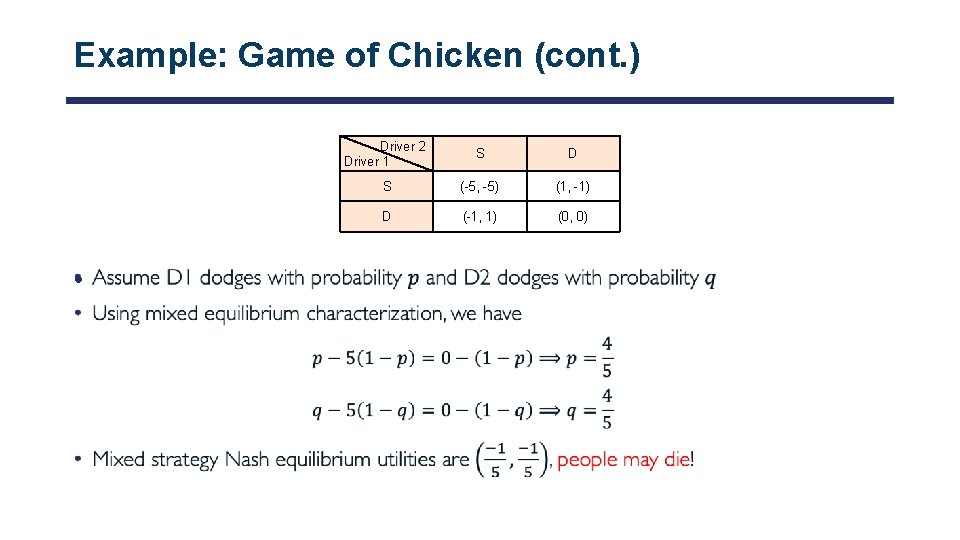
Example: Game of Chicken (cont. ) • Driver 2 Driver 1 S D S (-5, -5) (1, -1) D (-1, 1) (0, 0)

Example: Game of Chicken (cont. ) • Driver 2 Driver 1 S D (-5, -5) (1, -1) 0% 40% (-1, 1) (0, 0) 40% 20%

Characterization of Correlated Equilibrium •

Questions?

Acknowledgement • This lecture is a slightly modified version of ones prepared by • Asu Ozdaglar [MIT 6. 254] • Vincent Conitzer [Duke CPS 590. 4]