ECE 6340 Intermediate EM Waves Fall 2016 Prof

























- Slides: 48

ECE 6340 Intermediate EM Waves Fall 2016 Prof. David R. Jackson Dept. of ECE Notes 16 1

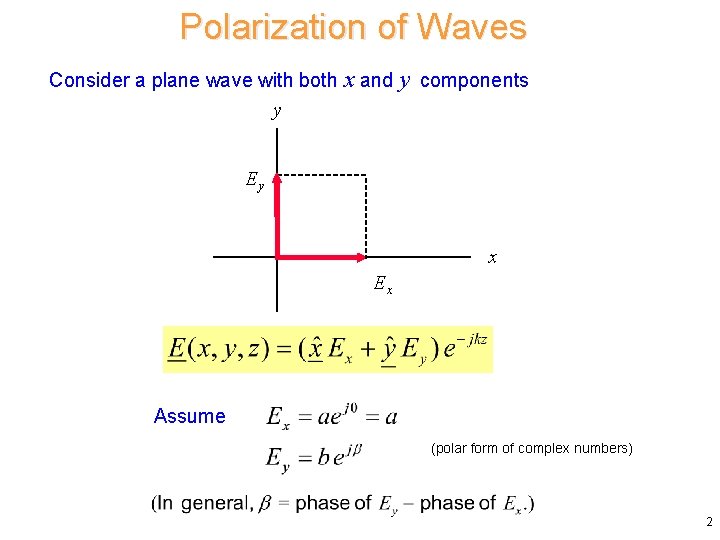
Polarization of Waves Consider a plane wave with both x and y components y Ey x Ex Assume (polar form of complex numbers) 2

Polarization of Waves (cont. ) Time Domain: At z=0 y E (t) |E (t)| (t) x Depending on b and , three different cases arise. 3

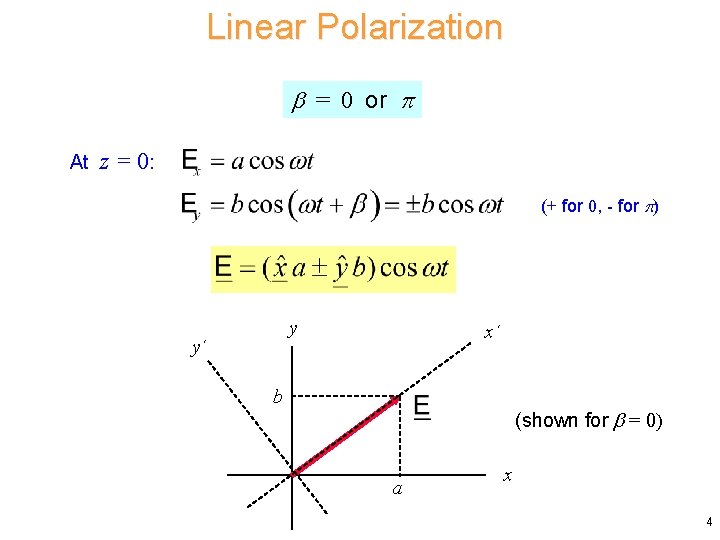
Linear Polarization = 0 or At z = 0: (+ for 0, - for ) y y´ x´ b (shown for = 0) a x 4

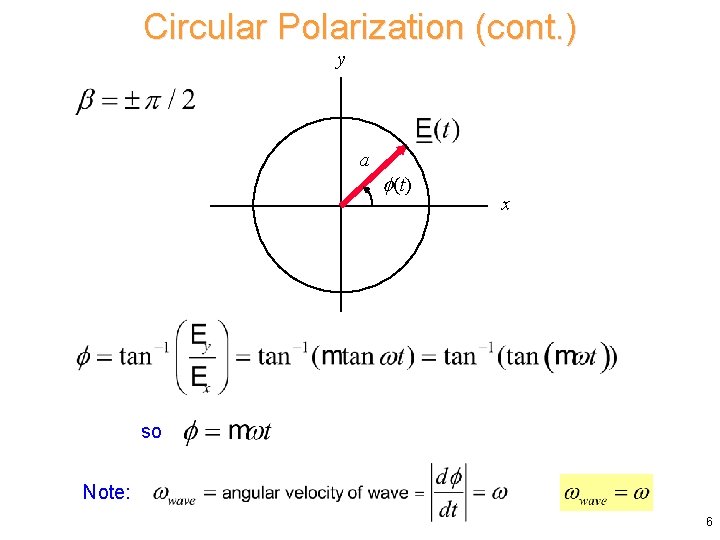
Circular Polarization b = a AND = /2 At z = 0: 5

Circular Polarization (cont. ) y a (t) x so Note: 6

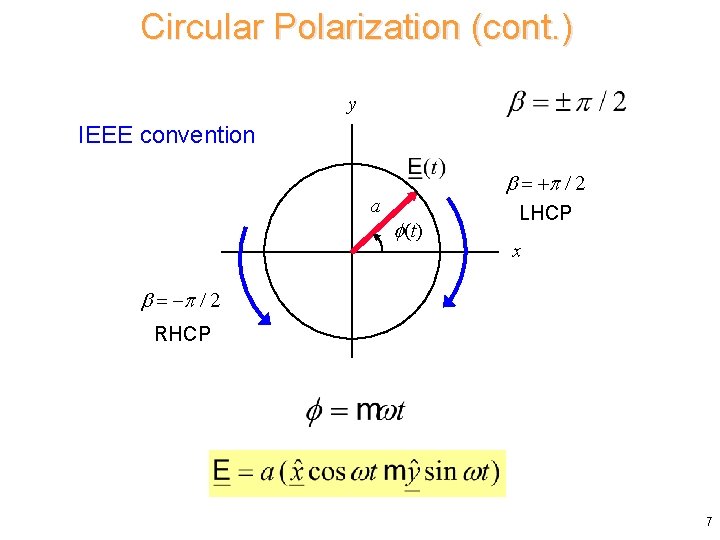
Circular Polarization (cont. ) y IEEE convention = + / 2 a (t) LHCP x = - / 2 RHCP 7

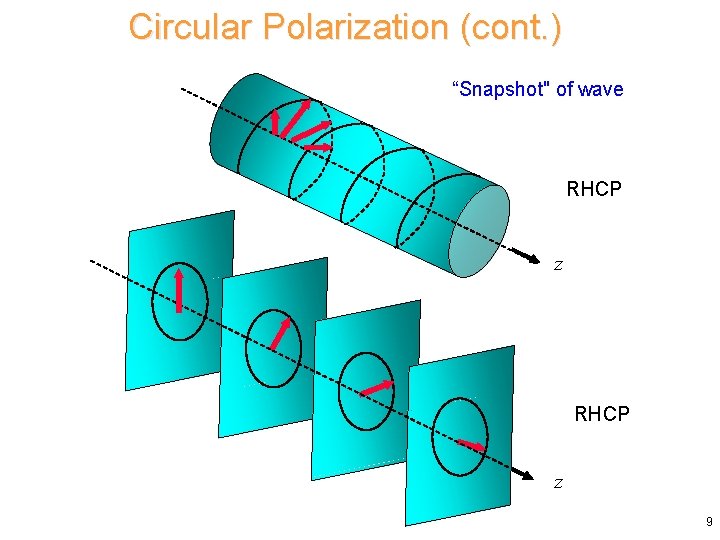
Circular Polarization (cont. ) Note: The rotation is space is opposite to that in time. Time and distance dependence: RHCP z=0 t=0 8

Circular Polarization (cont. ) “Snapshot" of wave RHCP z 9

Circular Polarization (cont. ) Animation of LHCP wave (Use pptx version in full-screen mode to see motion. ) http: //en. wikipedia. org/wiki/Circular_polarization 10

Unit Rotation Vectors RHCP ( = - / 2) LHCP ( = + / 2) Add: Subtract: 11

General Wave Representation Note: Any polarization can be written as combination of RHCP and LHCP waves. This could be useful in dealing with CP antennas. 12

Circularly Polarized Antennas Method 1: The antenna is fundamentally CP. A helical antenna for satellite reception is shown here. The helical antenna is shown radiating above a circular ground plane. 13

Circularly Polarized Antennas (cont. ) Method 2: Two perpendicular antennas are used, fed 90 o out of phase. y Vx = 1 + - Vy = -j +- x RHCP z A more complicated version using four antennas (omni CP) Two antennas are shown here being fed by a common feed point. Note: LHCP is radiated in the negative z direction. 14

Circularly Polarized Antennas (cont. ) Method 3: A single antenna is used, but two perpendicular modes are excited 90 o out of phase. (a) (b) (a) A square microstrip antenna with two perpendicular modes being excited. (b) A circular microstrip antenna using a single feed and slots. The feed is located at 45 o from the slot axis. (c) A square patch with two corners chopped off, fed at 45 o from the edge. (c) 15

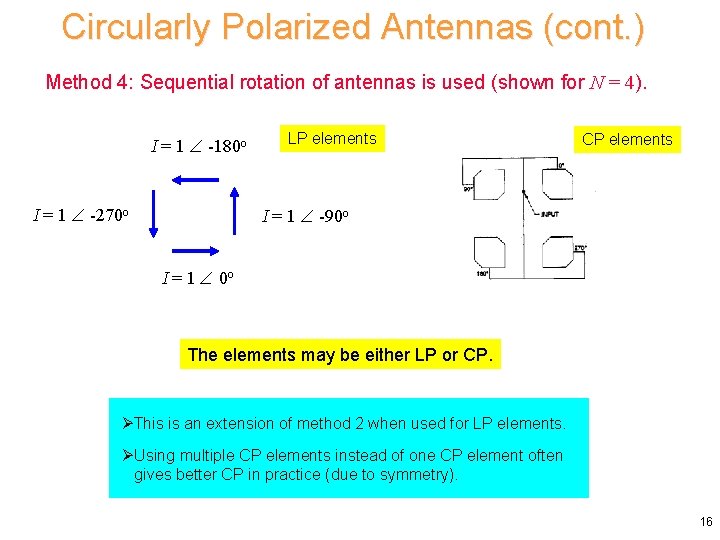
Circularly Polarized Antennas (cont. ) Method 4: Sequential rotation of antennas is used (shown for N = 4). I = 1 -180 o I = 1 -270 o LP elements CP elements I = 1 -90 o I = 1 0 o The elements may be either LP or CP. ØThis is an extension of method 2 when used for LP elements. Ø Using multiple CP elements instead of one CP element often gives better CP in practice (due to symmetry). 16

Pros and Cons of CP Pros § Alignment between transmit and receive antennas is not important. § The reception does not depend on rotation of the electric field vector that might occur†. § When a RHCP bounces off an object, it mainly changes to a LHCP wave. Therefore, a RHCP receive antenna will not be as sensitive to “multipath” signals that bound off of other objects. Cons § A CP system is usually more complicated and expensive. § Often, simple wire antennas are used for reception of signals in wireless communications, and hence they are already directly compatible with linear polarization. (Using a CP transmitted signal will result in 50% of the transmitted power being wasted, or a 3 d. B drop in the received signal). † Satellite transmission often uses CP because of Faraday rotation in the ionosphere. 17

Pros and Cons of CP (cont. ) Effects of alignment errors = alignment angle error TX-RX Gain Loss LP-LP cos 2 : The received signal can vary from zero d. B to - d. B CP-LP -3 d. B, no matter what the alignment LP-CP -3 d. B, no matter what the alignment CP-CP 0 d. B (polarizations same) or - d. B (polarizations opposite), no matter what the alignment 18

Examples of Polarization § AM Radio (0. 540 -1. 6 MHz): linearly polarized (vertical) (Note 1) § FM Radio (88 -108 MHz): linearly polarized (horizontal) § TV (VHF, 54 -216 MHz; UHF, 470 -698 MHz: linearly polarized (horizontal) (some transmitters are CP) § Cell phone antenna (about 2 GHz, depending on system): linearly polarized (direction arbitrary) § Cell phone base-station antennas (about 2 GHz, depending on system): often linearly polarized (dual-linear slant 45 o) (Note 2) § DBS Satellite TV (11. 7 -12. 5 GHz): transmits both LHCP and RHCP (frequency reuse) (Note 3) § GPS (1. 574 GHz): RHCP (Note 3) Notes: 1) Low-frequency waves travel better along the earth when they are polarized vertically instead of horizontally. 2) Slant linear is used to switch between whichever polarization is stronger. 3) Satellite transmission often uses CP because of Faraday rotation in the ionosphere. 19

Elliptical Polarization Includes all other cases § 0 or (not linear) § / 2 (not CP) § = / 2 and b a (not CP) y (t) x Ellipse 20

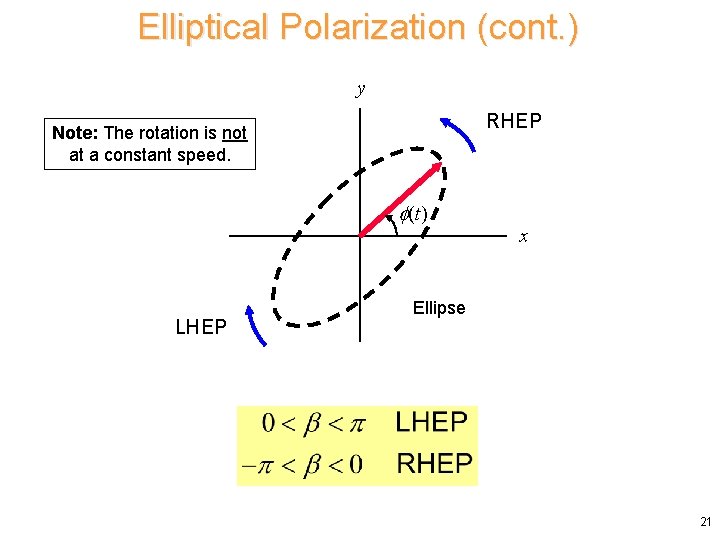
Elliptical Polarization (cont. ) y RHEP Note: The rotation is not at a constant speed. (t) LHEP x Ellipse 21

Proof of Ellipse Property so 22

Proof of Ellipse Property (cont. ) Consider the following quadratic form: 23

Proof of Ellipse Property (cont. ) Discriminant: From analytic geometry: so Hence, this is an ellipse. If = 0 or we have = 0, and this is linear polarization. 24

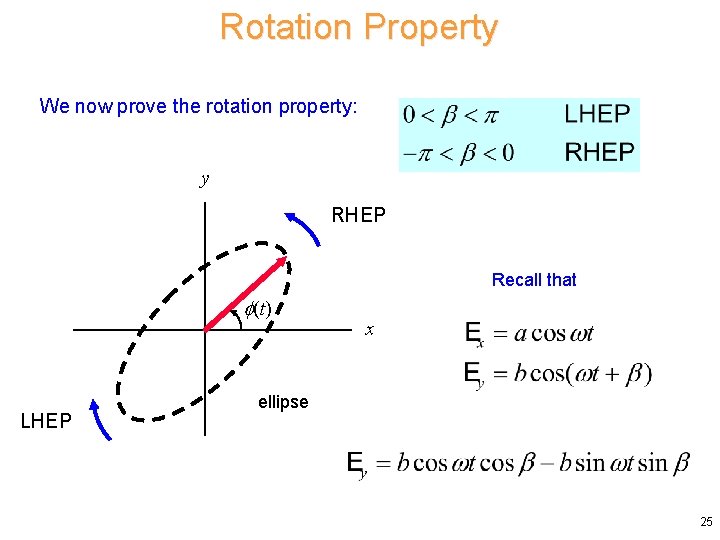
Rotation Property We now prove the rotation property: y RHEP Recall that (t) LHEP x ellipse 25

Rotation Property (cont. ) Hence Take the derivative: so (proof complete) 26

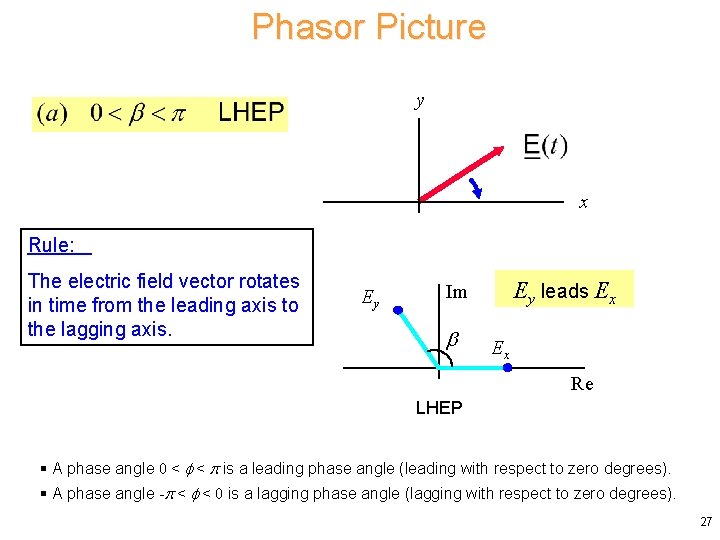
Phasor Picture y x Rule: The electric field vector rotates in time from the leading axis to the lagging axis. Ey Ey leads Ex Im Ex Re LHEP § A phase angle 0 < < is a leading phase angle (leading with respect to zero degrees). § A phase angle - < < 0 is a lagging phase angle (lagging with respect to zero degrees). 27

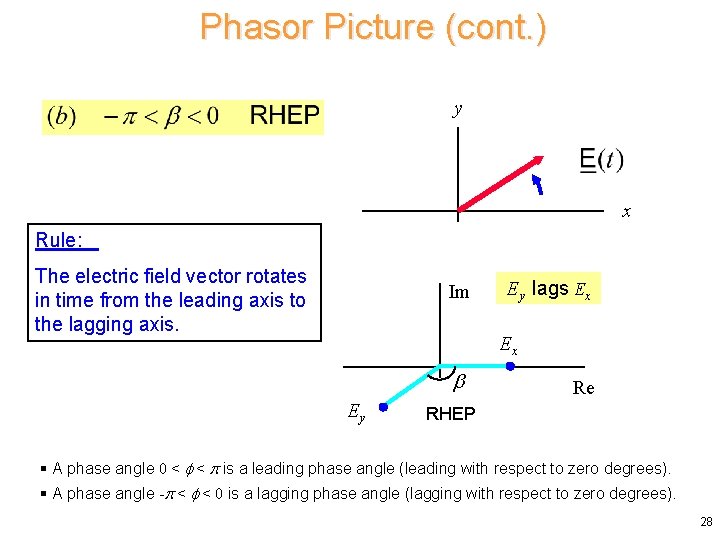
Phasor Picture (cont. ) y x Rule: The electric field vector rotates in time from the leading axis to the lagging axis. Im Ey lags Ex Ex Ey Re RHEP § A phase angle 0 < < is a leading phase angle (leading with respect to zero degrees). § A phase angle - < < 0 is a lagging phase angle (lagging with respect to zero degrees). 28

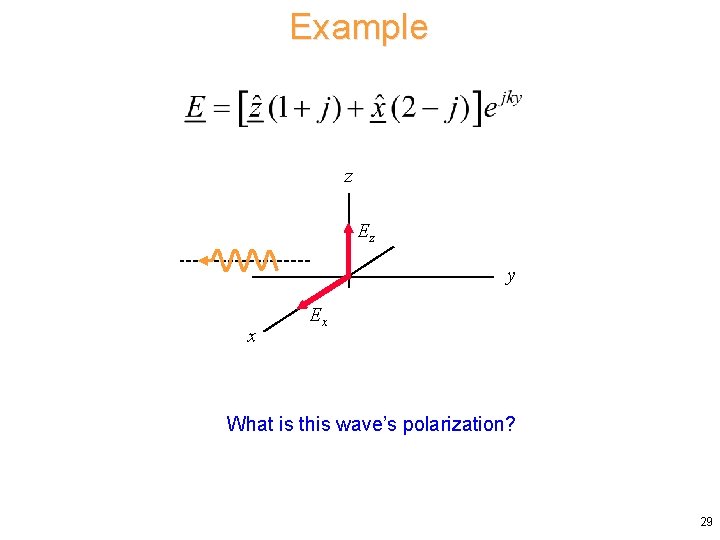
Example z Ez y x Ex What is this wave’s polarization? 29

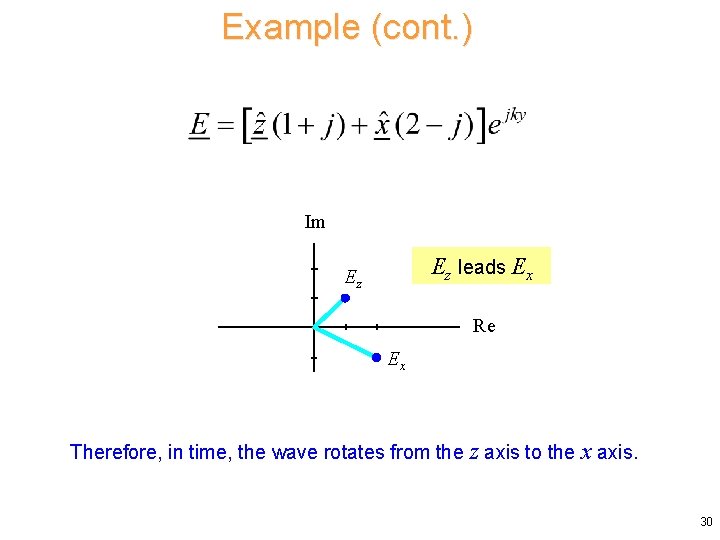
Example (cont. ) Im Ez leads Ex Ez Re Ex Therefore, in time, the wave rotates from the z axis to the x axis. 30

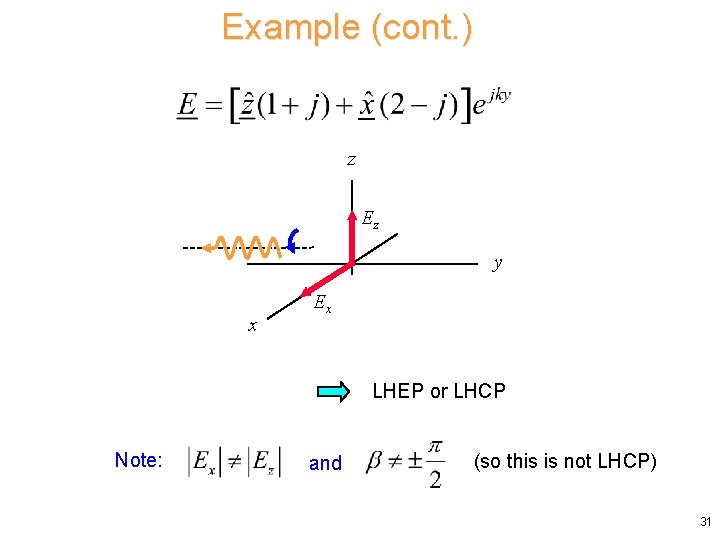
Example (cont. ) z Ez y x Ex LHEP or LHCP Note: and (so this is not LHCP) 31

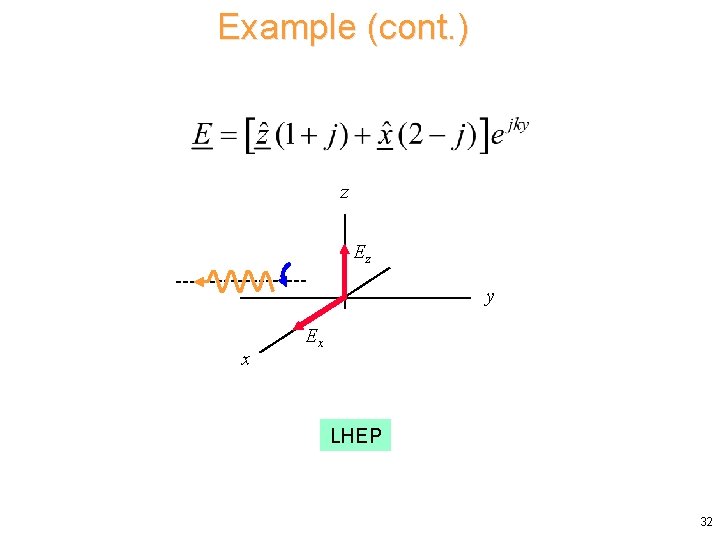
Example (cont. ) z Ez y x Ex LHEP 32

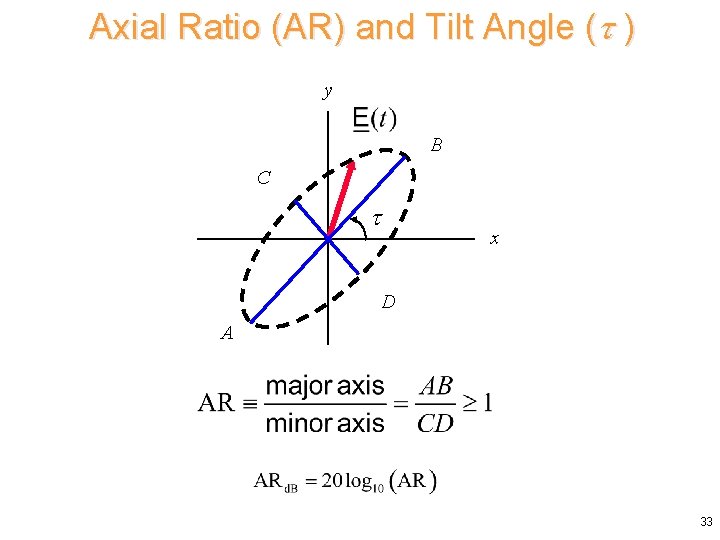
Axial Ratio (AR) and Tilt Angle ( ) y B C x D A 33

Axial Ratio (AR) and Tilt Angle ( ) We first calculate : Axial Ratio Tilt Angle (-90 o < < 90 o) Note: The tilt angle is ambiguous by the addition of 90 o. (We cannot tell the difference between the major and minor axes. ) 34

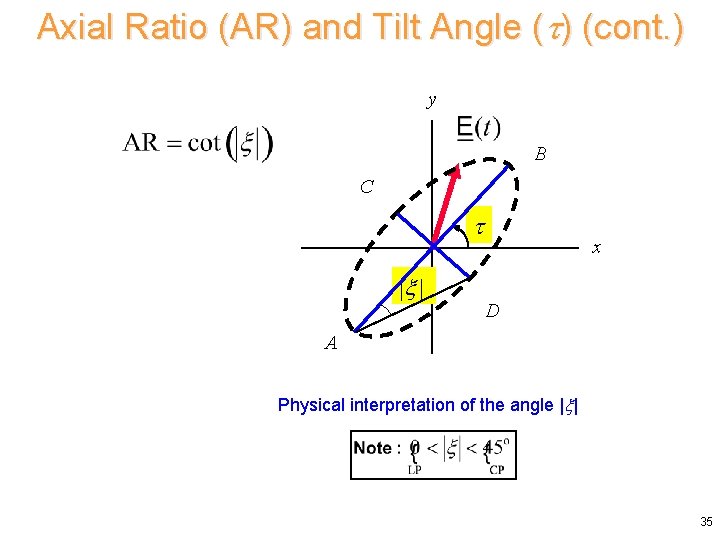
Axial Ratio (AR) and Tilt Angle ( ) (cont. ) y B C | | x D A Physical interpretation of the angle | | 35

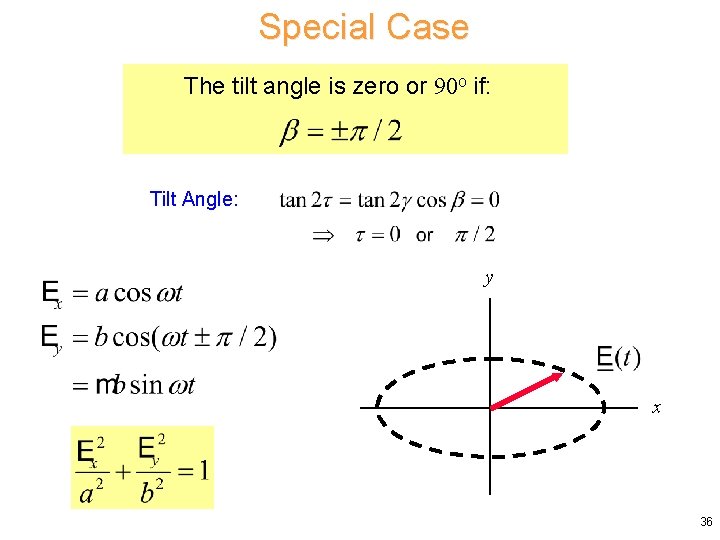
Special Case The tilt angle is zero or 90 o if: Tilt Angle: y x 36

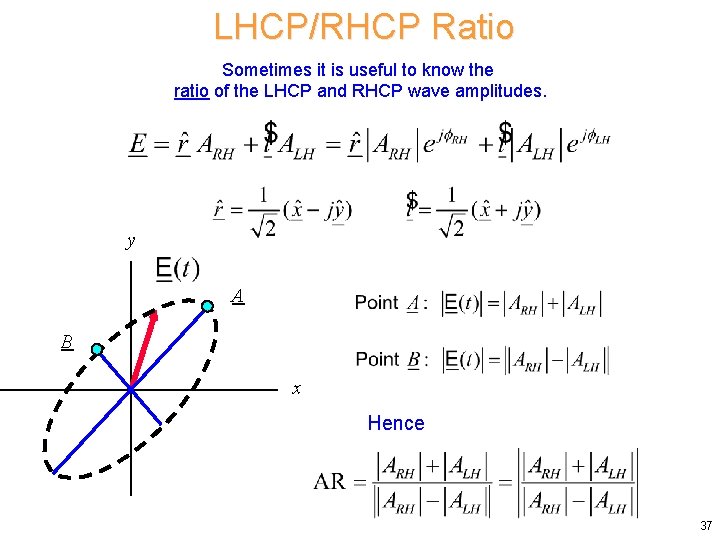
LHCP/RHCP Ratio Sometimes it is useful to know the ratio of the LHCP and RHCP wave amplitudes. y A B x Hence 37

LHCP/RHCP Ratio (Cont. ) Hence or (Use whichever sign gives AR > 0. ) From this we can also solve for the ratio of the CP components, if we know the axial ratio: (We can’t tell which one is correct from knowing only the AR. ) 38

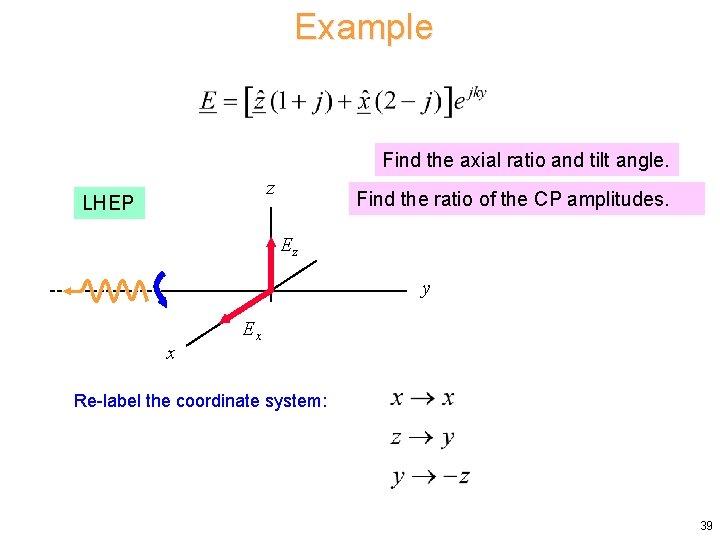
Example Find the axial ratio and tilt angle. z LHEP Find the ratio of the CP amplitudes. Ez y x Ex Re-label the coordinate system: 39

Example (cont. ) y Ez LHEP z x Ex 40

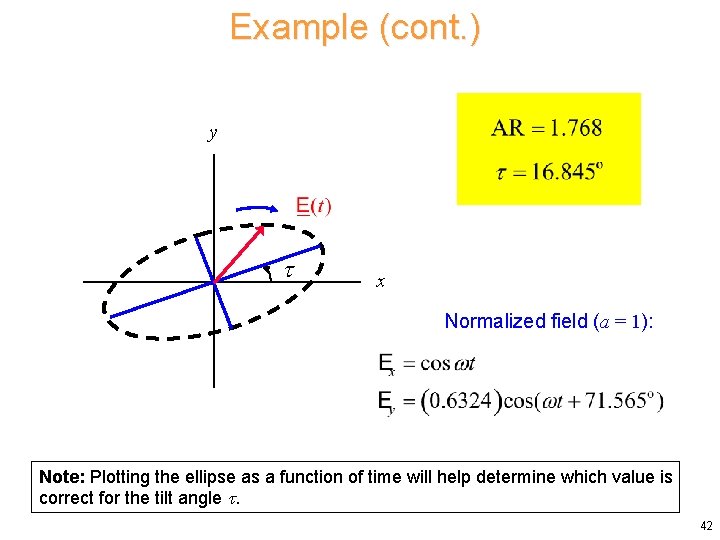
Example (cont. ) Formulas Results LHEP 41

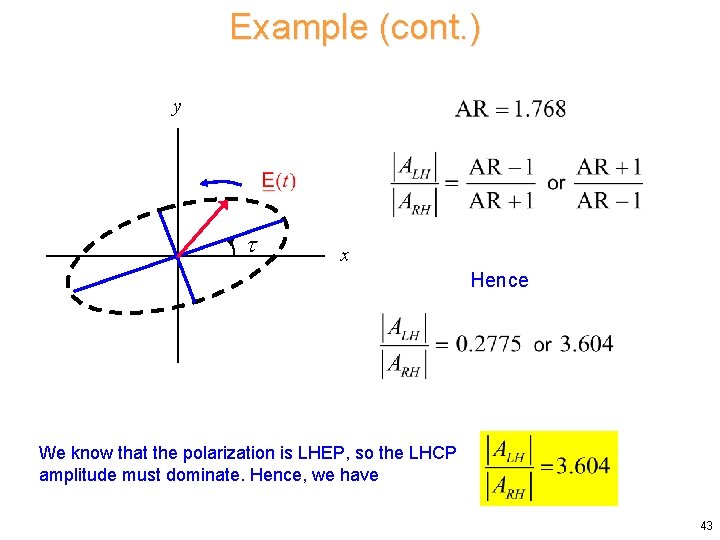
Example (cont. ) y x Normalized field (a = 1): Note: Plotting the ellipse as a function of time will help determine which value is correct for the tilt angle . 42

Example (cont. ) y x Hence We know that the polarization is LHEP, so the LHCP amplitude must dominate. Hence, we have 43

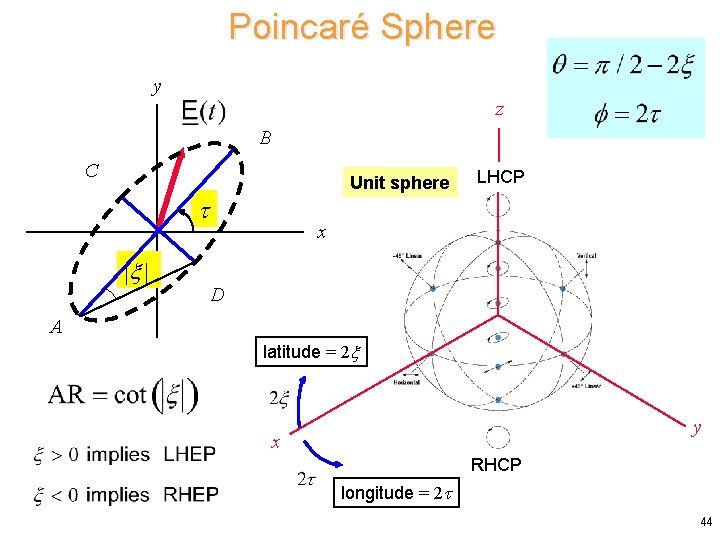
Poincaré Sphere y z B C Unit sphere | | LHCP x D A latitude = 2 y x RHCP longitude = 2 44

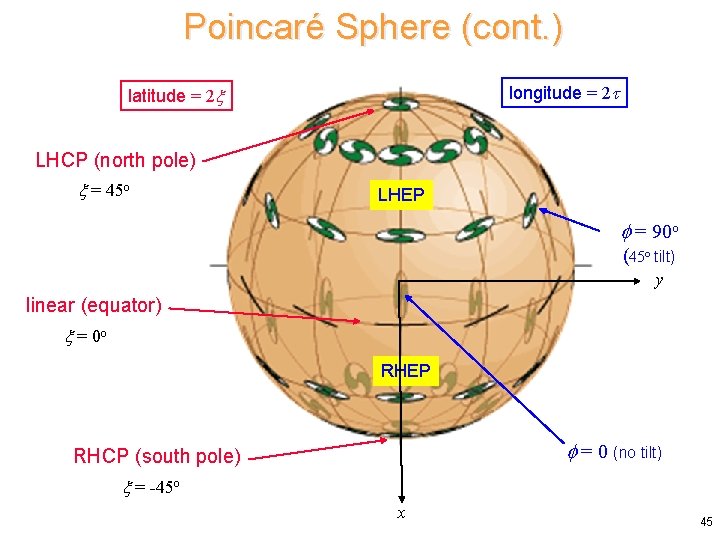
Poincaré Sphere (cont. ) longitude = 2 latitude = 2 LHCP (north pole) = 45 o LHEP = 90 o (45 o tilt) y linear (equator) = 0 o RHEP = 0 (no tilt) RHCP (south pole) = -45 o x 45

Poincaré Sphere (cont. ) View in full-screen mode to watch the “world spinning”. 46

Poincaré Sphere (cont. ) Two diametrically opposite points on the Poincaré sphere have the property that the electric field vectors (in the phasor domain) are orthogonal in the complex sense. (A proof is given in the Appendix. ) z Examples A y x B (orthogonal in the complex power sense) 47

Appendix Proof of orthogonal property z From examining the polarization equations: A y x B Hence 48
 Dfd 6340
Dfd 6340 Thread priorities
Thread priorities Similarities of mechanical and electromagnetic waves
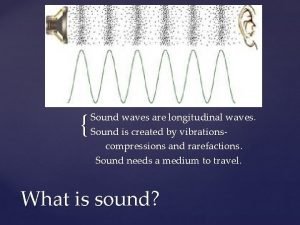
Similarities of mechanical and electromagnetic waves Sound waves are electromagnetic waves true or false
Sound waves are electromagnetic waves true or false Mechanical wave and electromagnetic wave
Mechanical wave and electromagnetic wave Difference between electromagnetic and mechanical waves
Difference between electromagnetic and mechanical waves The wave chapter 13
The wave chapter 13 Whats a reflected sound wave
Whats a reflected sound wave Carbon dioxide temperature
Carbon dioxide temperature Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Examples of mechanical and electromagnetic waves
Examples of mechanical and electromagnetic waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Surface waves and body waves
Surface waves and body waves Is a seismic wave mechanical or electromagnetic
Is a seismic wave mechanical or electromagnetic Compare and contrast p waves and s waves using venn diagram
Compare and contrast p waves and s waves using venn diagram What do all waves transmit
What do all waves transmit What are constructive waves
What are constructive waves Free fall 2016
Free fall 2016 Words their way intermediate spelling inventory
Words their way intermediate spelling inventory Leonard herman intermediate school
Leonard herman intermediate school Stehlik intermediate school
Stehlik intermediate school Present simple exercises pre intermediate
Present simple exercises pre intermediate Unit 8 upper intermediate
Unit 8 upper intermediate Mood food vocabulary
Mood food vocabulary Novice intermediate advanced
Novice intermediate advanced Fasciola hepatica
Fasciola hepatica Toxoplasma intermediate host
Toxoplasma intermediate host Della icenhower intermediate school
Della icenhower intermediate school Distingration
Distingration Speech emergence stage activities
Speech emergence stage activities Lp miles elementary
Lp miles elementary Salina intermediate school
Salina intermediate school Novice intermediate advanced
Novice intermediate advanced Book value per ordinary share
Book value per ordinary share Explosive disorder
Explosive disorder Foundation intermediate advanced
Foundation intermediate advanced Napier intermediate
Napier intermediate Naenae intermediate
Naenae intermediate Intermediate filament tetramer
Intermediate filament tetramer Intermediate and transition state
Intermediate and transition state Lathrop intermediate school yearbook
Lathrop intermediate school yearbook Lathrop intermediate school
Lathrop intermediate school Chapter 17 intermediate accounting solutions
Chapter 17 intermediate accounting solutions Introduction of cytoskeleton
Introduction of cytoskeleton Khan academy intermediate value theorem
Khan academy intermediate value theorem Intermediate pressure system
Intermediate pressure system What is intermediate form
What is intermediate form Intermediate crime scene investigation #2106
Intermediate crime scene investigation #2106 Intermediate code generator
Intermediate code generator