CS 212 LECTURE 02 PROGRAMMING LANGUAGES TRY THIS

CS 212 LECTURE 02 PROGRAMMING LANGUAGES

TRY THIS Let L be a language over ={a, b} consists of all even-length strings Let L be a language over ={a} consists of even number of a. 2

REGULAR EXPRESSION Let be an alphabet. The regular sets over Arer defined recursively as follows: i) Basis: , and a, for every a , are regular expressions over ii) Recursive step: Let u and v be regular expressions over . The expressions (u + v) (u*) are regular expressions over . III. Closure: u is a regular expression over only if it can be obtained from the basis elements by a finite number of applications of the recursive step. 3

REGULAR EXPRESSION Example Language L is the set of strings over ={a, b} that Begin and end with a and contain at least one b. L = a(a+b)*b(a+b)*a From basis : a and b are regular expression Apply union and kleen star operation produce (a+b)*, then concat a and (a+b)* = a(a+b)* then concat a(a+b)* and b = a(a+b)*b then concat a(a+b)*b and (a+b)* = a(a+b)*b(a+b)* then concat a(a+b)*b(a+b)* and a = a(a+b)*b(a+b)*a is a regular expression. 4

REGULAR EXPRESSION Example A regular expression for the set of strings over ={a, b} that contain exactly two b’s. Any number of a’s may occur before, between, and after b’s. r = a*ba*ba* Example The regular expression for the set of strings over ={a, b, c} containing the substring bc. r = (a+b+c)*bc(a+b+c)* 5

REGULAR EXPRESSION Example A regular expression for the set of strings over ={a, b} that contain even number of a’s. String in r : , aa, aba, babab, b, babbabaa String not in r : a, ba, ab, aaa, ababa, baaa, … r = ( b + (ab*ab*))* 6

REGULAR EXPRESSION Example A regular expression for the set of strings over ={a, b} that count number of a’s divisible by 3. String in r : , aaa, bababa, aaaaaa, baaaaaab, b, bbb, bababab, …. String not in r : a, ba, ab, aa, abba, babaaba, … r = ( b + (ab*ab*ab*))* 7

REGULAR EXPRESSION Example The regular expression for the set of strings over ={a, b} with an even number of a’s and an even number of b’s Strings in this language will have clumps of 3 kinds: Type 1 — aa Type 2 — bb Type 3 — starting with ab (or with ba ) and eventually balancing with another ab or ba. So: ( aa+bb+ ((ab+ba)(aa+bb)*(ab+ba)) )* 8

REGULAR EXPRESSION The regular expression R is the string over ={a, b} with an odd number of a’s. String in R : a, ab, bab, abbbb, bbbba, bbabbb, …, aaa, ababa, aabbbba, abababbb, abbbabbabbb, bbbbabbabbabbb, … String not in R : , aa, baa, aab, bbaa, baba, abab, aaaa, … The odd number of a’s came from ‘a’ concat with ‘aa’. bbb…. babbb…babbb…b So that , R = b*ab*(b*ab*ab*)* 9

REGULAR EXPRESSION EXAMPLE The regular expression R is the string over ={a, b} ending with b and not containing aa. String in R : b, ab, bab, abb. . b, abab, bb. . b, ababb. . b, bb. . bab String not in R : , aa, baa, bbaa, aabb, aba, aaaab, … So, string must be the combination of b and ab. The two smallest string are b, ab. R= ? (b + ab) , R = (b + ab)*(b+ab) 10

TRY THIS The regular expression of the string over ={a, b, c} in which all the a’s precede the b’s which in turn precede the c’s. The regular expression of the string over ={0, 1} in which the string end with 1 and does not contain the substring 00. The regular expression of the string over ={a, b} consists of all odd-length strings 11

TRY THIS The regular expression of the string over ={a, b, c} in which all the a’s precede the b’s which in turn precede the c’s, but without the empty string. The regular expression of the string over ={a, b, c} that begin with a, contain exactly two b's, and end with cc. The regular expression of the string over ={a, b, c} that do not contain substring aa. 12

TRY THIS The regular expression of the string over ={a, b} with an even number of a's or an odd number of b's. The regular expression of the string over ={a, b, c} with an even length and contain exactly one a. The regular expression of the string over ={a, b} with an odd length and contain exactly two b’s. 13

WHAT IS AUTOMATA THEORY? • An automaton is an abstract model of a digital computer. • Alan Turing (1912 - 1954) • Father of modern computer science • English mathematician • Studied abstract machines called Turing machines even before computers existed 14

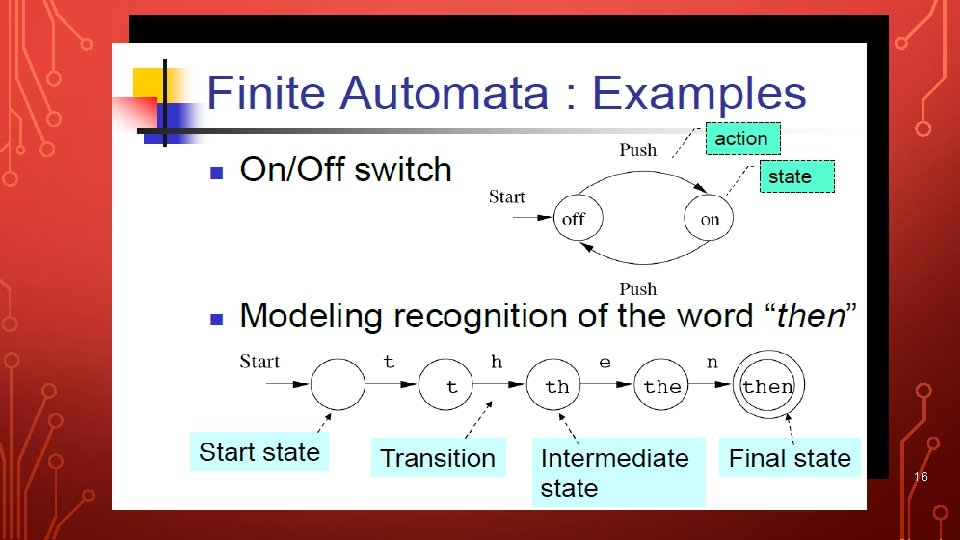
FINITE AUTOMATA • Finite automata are computing devices that accept or recognize regular languages. 15

16

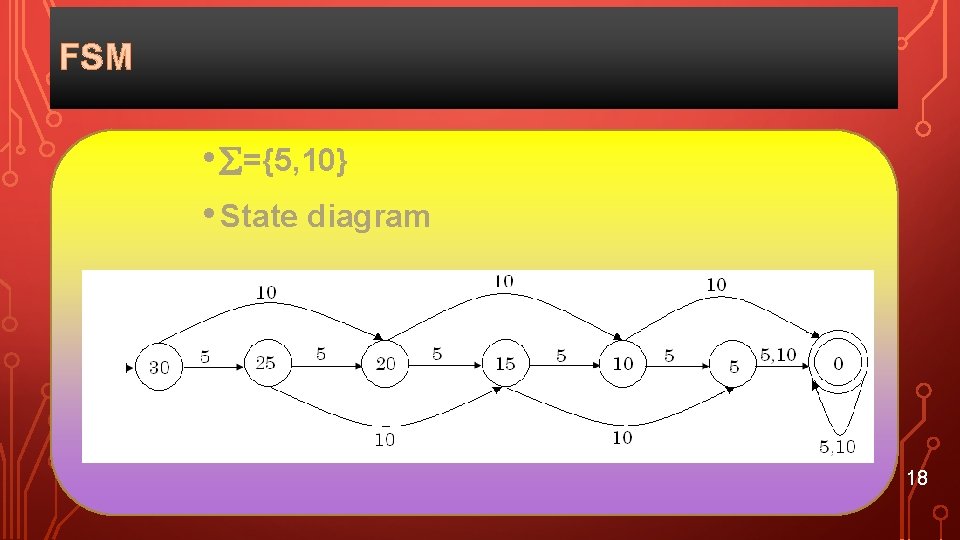
FINITE STATE MACHINE • Let think about a soda vending machine which accept only 5 and 10 Baht coin. • A soda bottle cost 30 Baht. • Now we have 7 states to put the coin. • Start state need 30 Baht, next state need 25, 20, 15, 10, 5, and a final state need 0 Baht. • Let draw a state diagram for the machine 17

FSM • ={5, 10} • State diagram 18

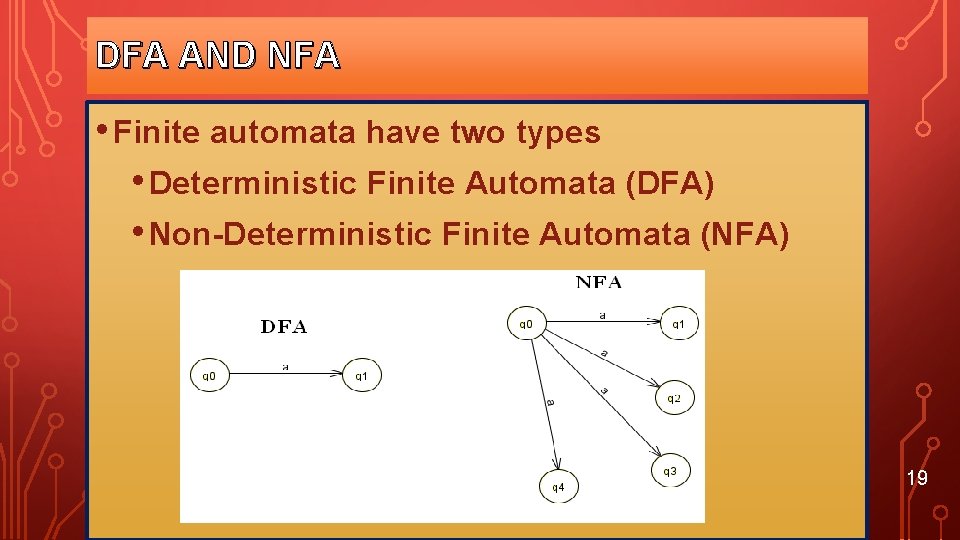
DFA AND NFA • Finite automata have two types • Deterministic Finite Automata (DFA) • Non-Deterministic Finite Automata (NFA) 19

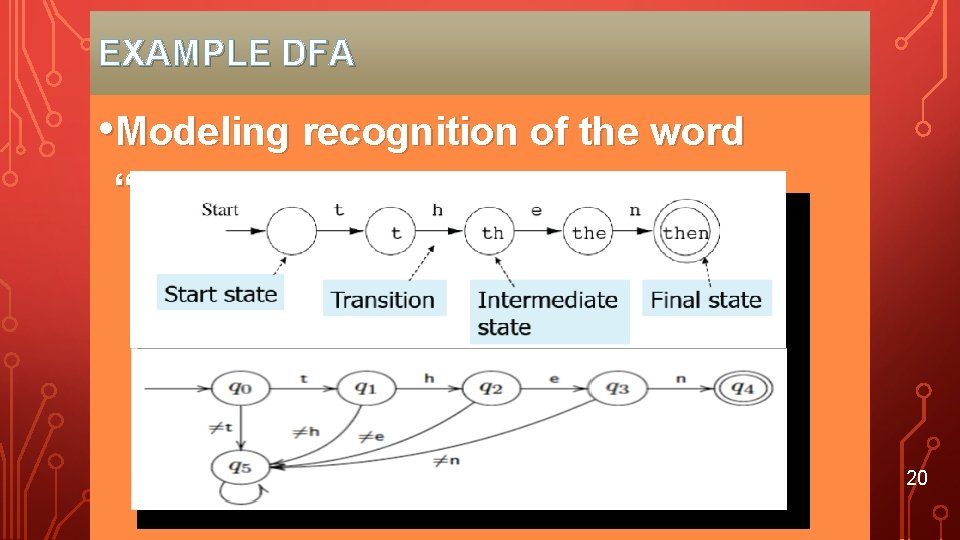
EXAMPLE DFA • Modeling recognition of the word “then” 20

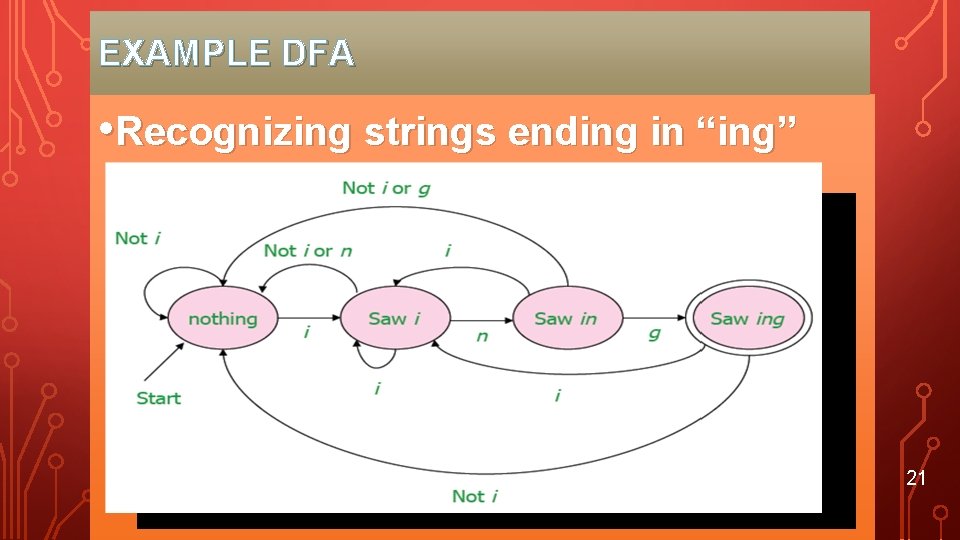
EXAMPLE DFA • Recognizing strings ending in “ing” 21

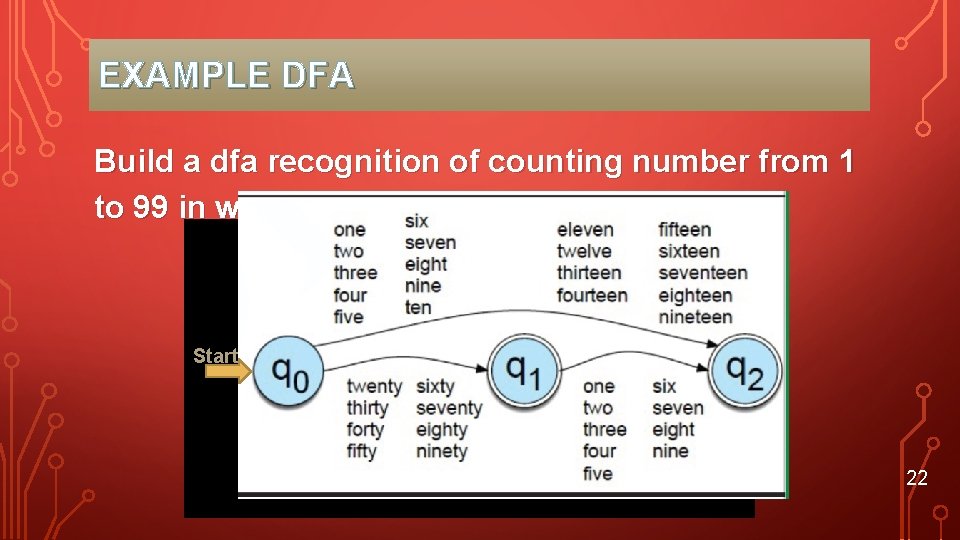
EXAMPLE DFA Build a dfa recognition of counting number from 1 to 99 in word. Start 22

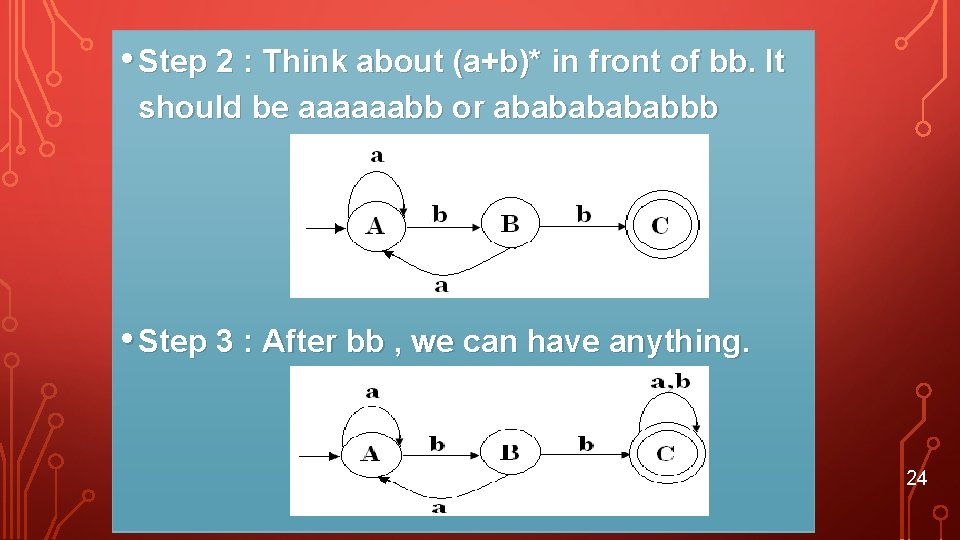
EXAMPLE DFA Regular expression r over ={a, b} r = (a+b)*bb(a+b)* Draw a state diagram of r Step 1 : Think about the smallest string , should be bb 23

• Step 2 : Think about (a+b)* in front of bb. It should be aaaaaabb or abababbb • Step 3 : After bb , we can have anything. 24

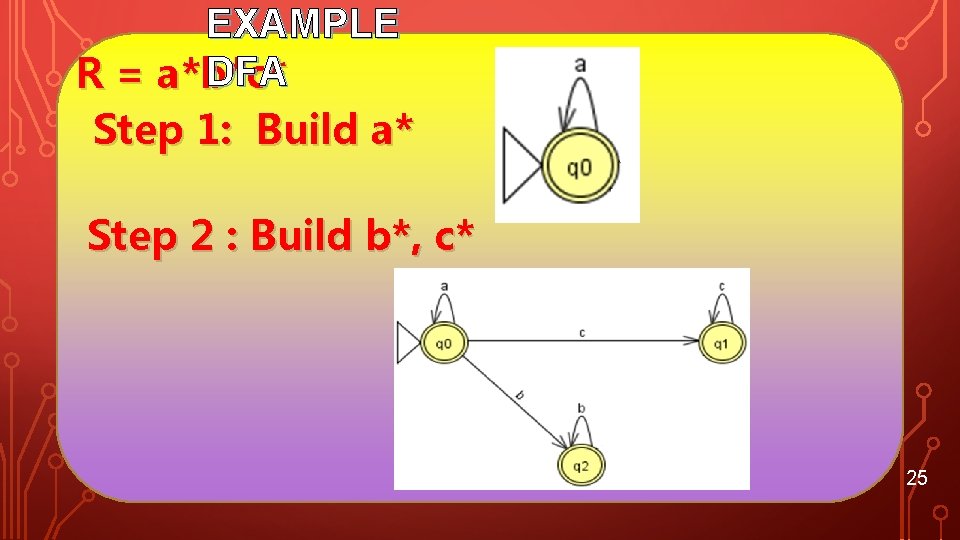
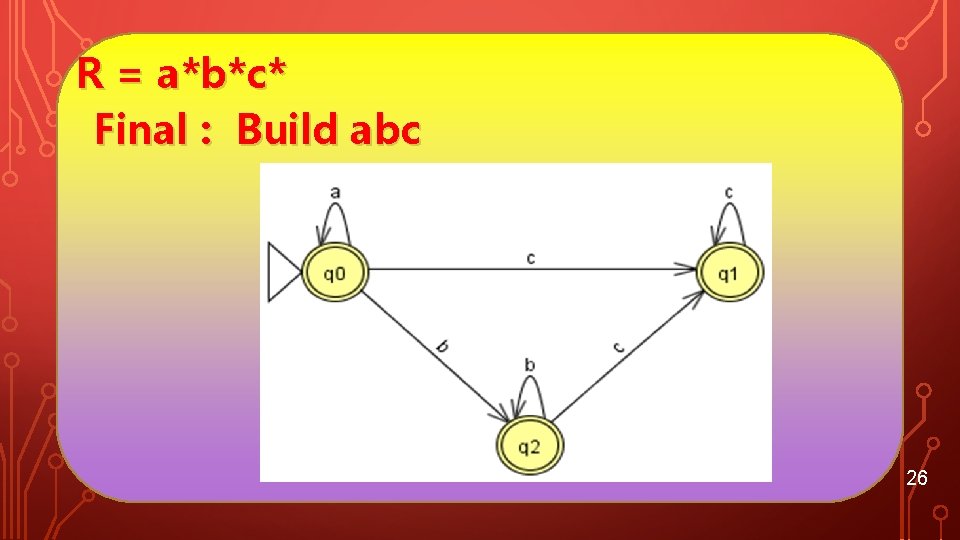
EXAMPLE DFA R = a*b*c* Step 1: Build a* Step 2 : Build b*, c* 25

R = a*b*c* Final : Build abc 26

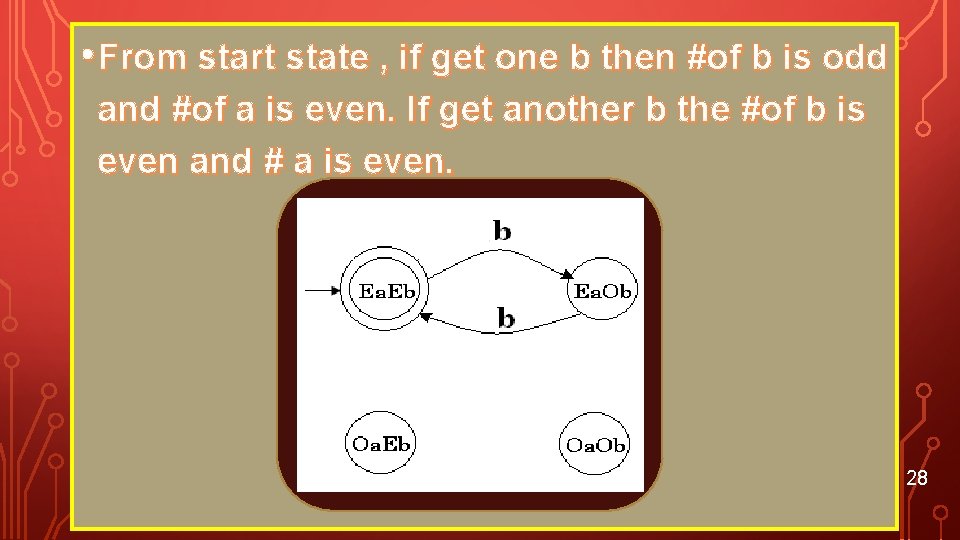
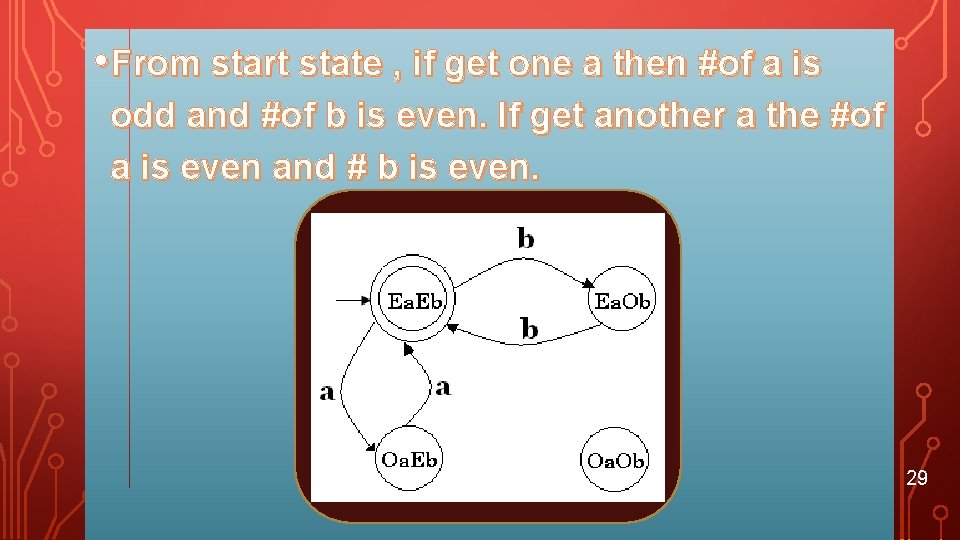
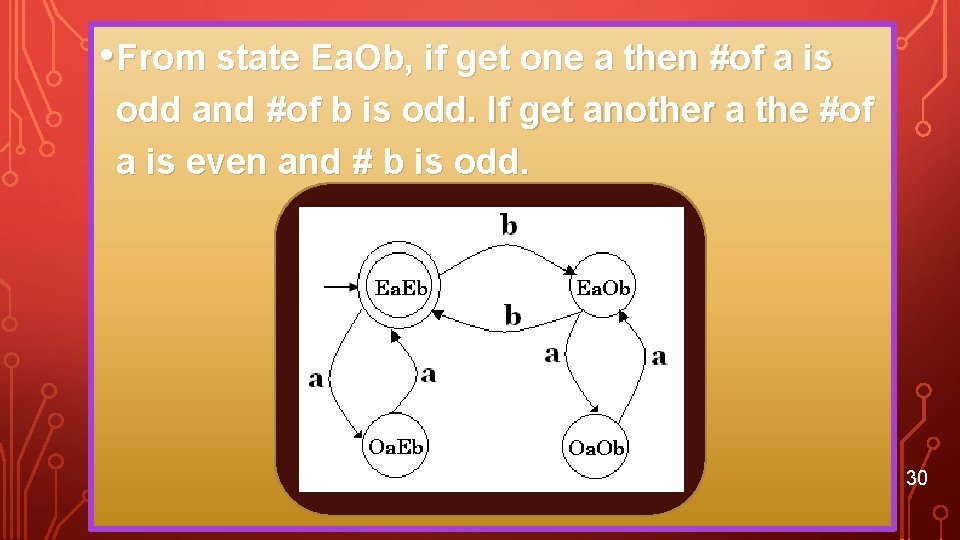
EXAMPLE • L is a language over ={a, b} which have the even number of a and even number of b • Step 1: is in L, aa, bb, abab, aabb, aaaabb, aabbaa … are in L. We should have 4 states. 1) # of a and # of b is even 2) # of a is even and # of b is odd 3) # of a is odd and # of b is even 4) # of a is odd and # of b is odd 27

• From start state , if get one b then #of b is odd and #of a is even. If get another b the #of b is even and # a is even. 28

• From start state , if get one a then #of a is odd and #of b is even. If get another a the #of a is even and # b is even. 29

• From state Ea. Ob, if get one a then #of a is odd and #of b is odd. If get another a the #of a is even and # b is odd. 30

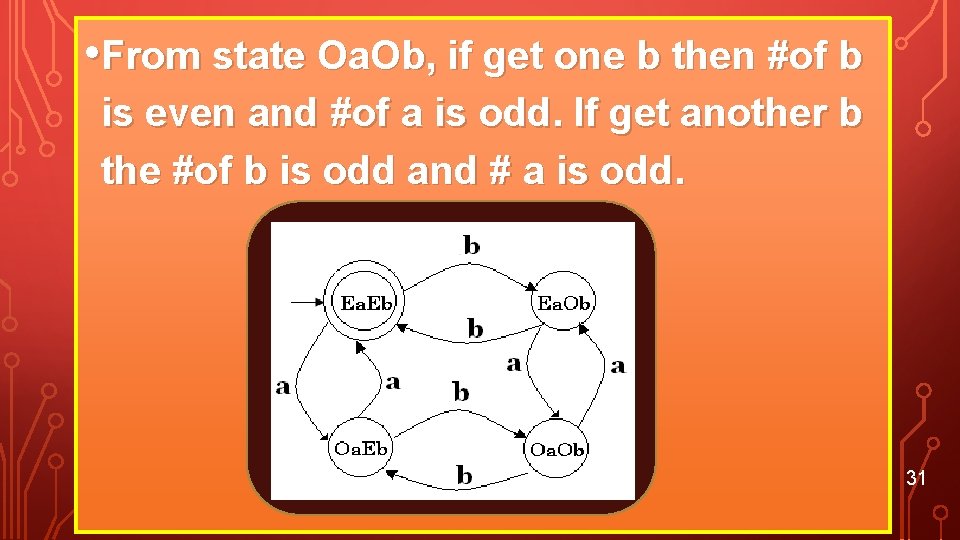
• From state Oa. Ob, if get one b then #of b is even and #of a is odd. If get another b the #of b is odd and # a is odd. 31

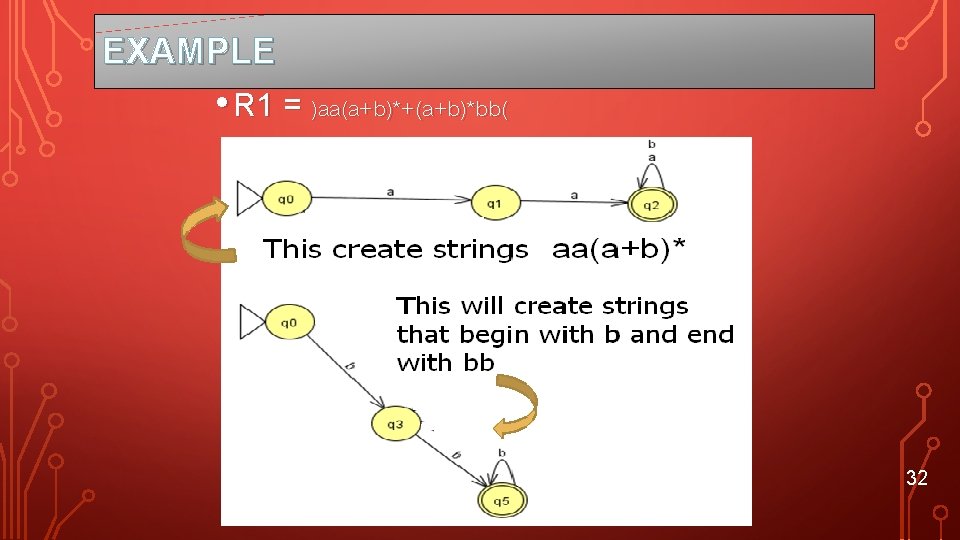
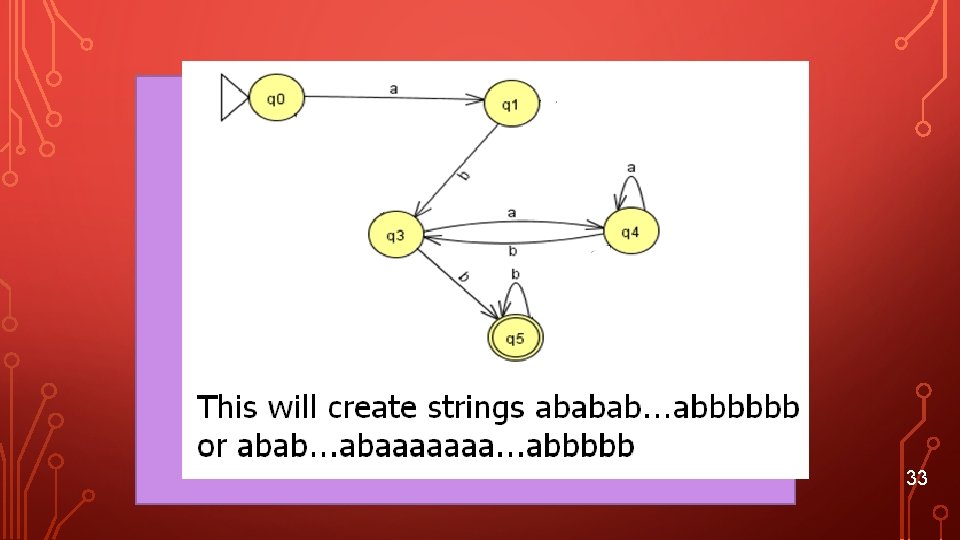
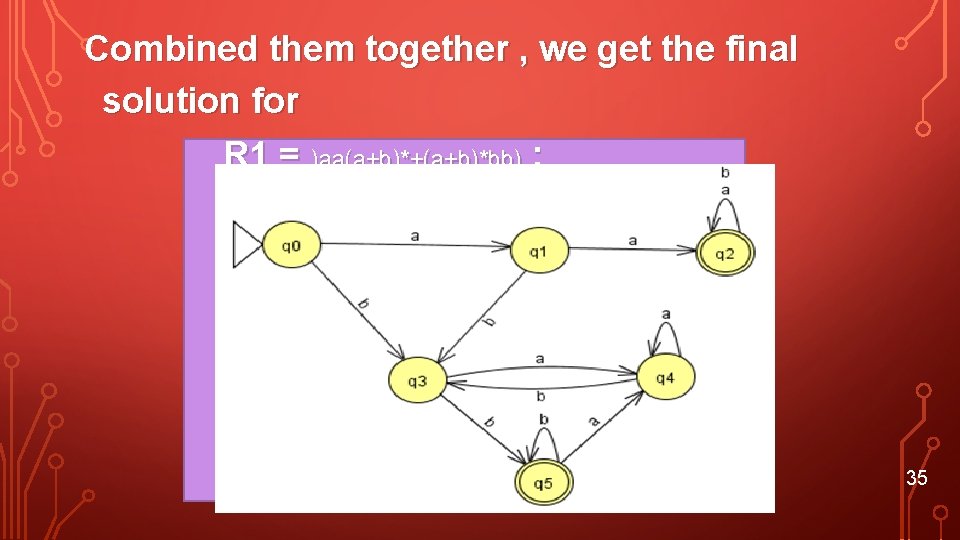
EXAMPLE • R 1 = )aa(a+b)*+(a+b)*bb( 32

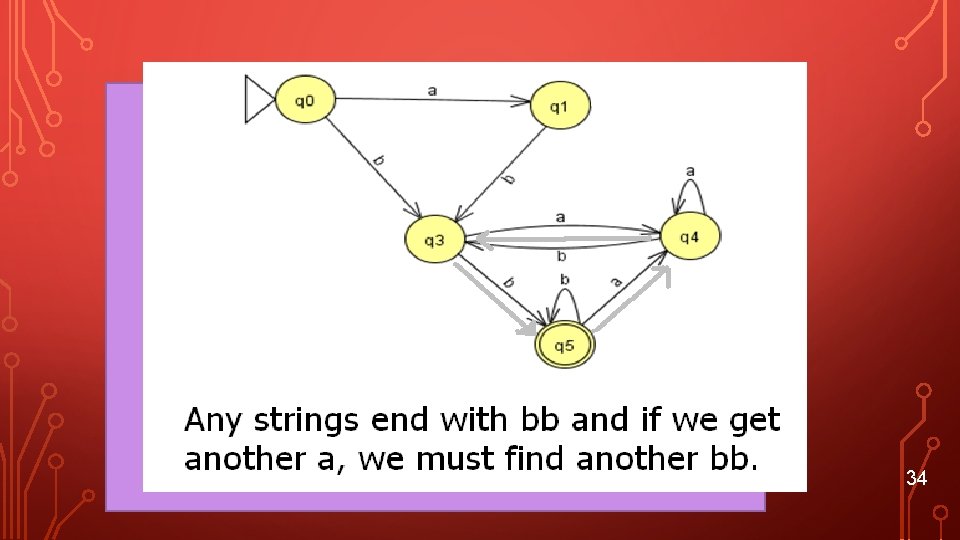
33

34

Combined them together , we get the final solution for R 1 = )aa(a+b)*+(a+b)*bb) : 35

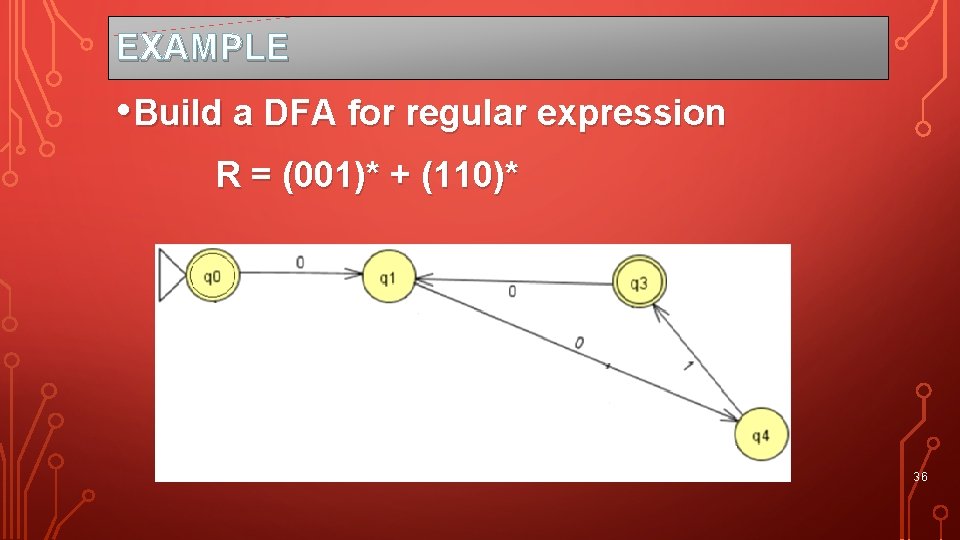
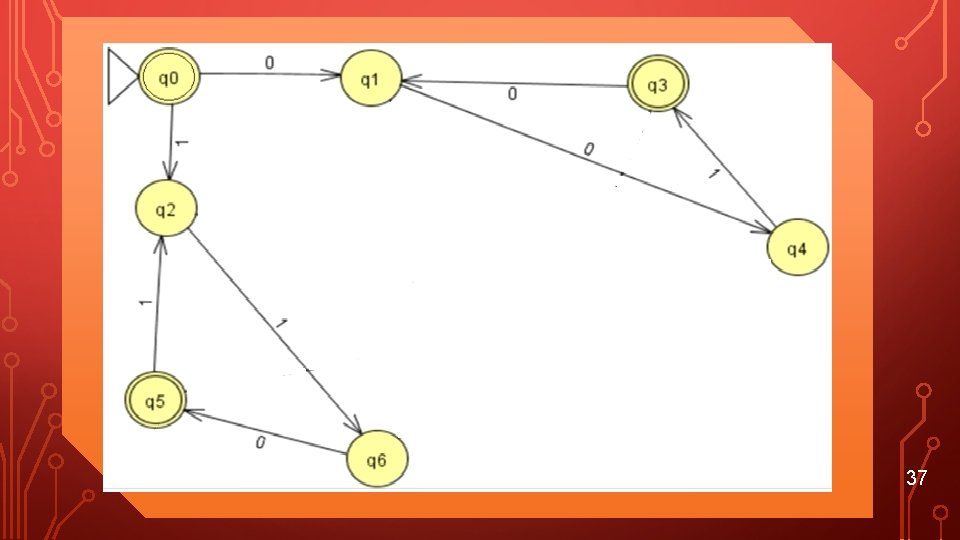
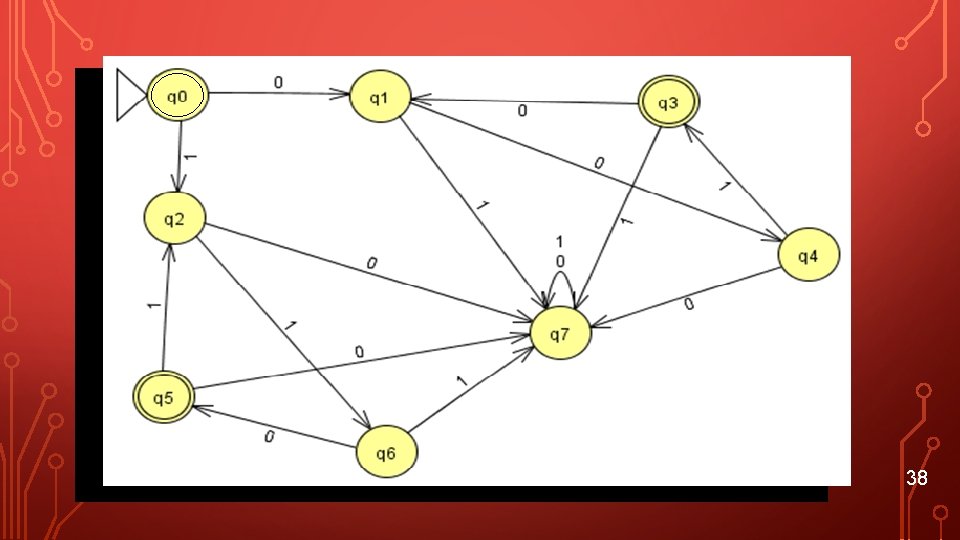
EXAMPLE • Build a DFA for regular expression R = (001)* + (110)* 36

37

38

TRY THIS No. 1 : Build a DFA that accept a regular expression R = (1+01)+ over ={0, 1} No. 2 : Build a DFA that accept all words that start with triple letter over ={a, b}. ( R = (aaa+bbb)(a+b)* ) No. 3 : Build a DFA that accept all words with even count of letters having “a” in an even position from the start, where the first letter is letter number one over ={a, b}. ( R = (a+b)a((a+b)a)* ) No. 4 : Build a DFA that accept set of strings where the number of 0 s in every string is multiple of 3 over ={0, 1}. ( R = (1+ 01*01*0)* ) No. 5 : Build a DFA that accept set of strings the odd number of 39