CS 212 LECTURE 07 PROGRAMMING LANGUAGES PREDICTIVE PARSING

CS 212 LECTURE 07 PROGRAMMING LANGUAGES

PREDICTIVE PARSING 2

PREDICTIVE PARSING AND LEFT FACTORING Recall the grammar • E → T + E | T • T → int | int * T | ( E( Impossible to predict because • For T two productions start with int • For E it is not clear how to predict • A grammar must be left-factored before use predictive parsing 3

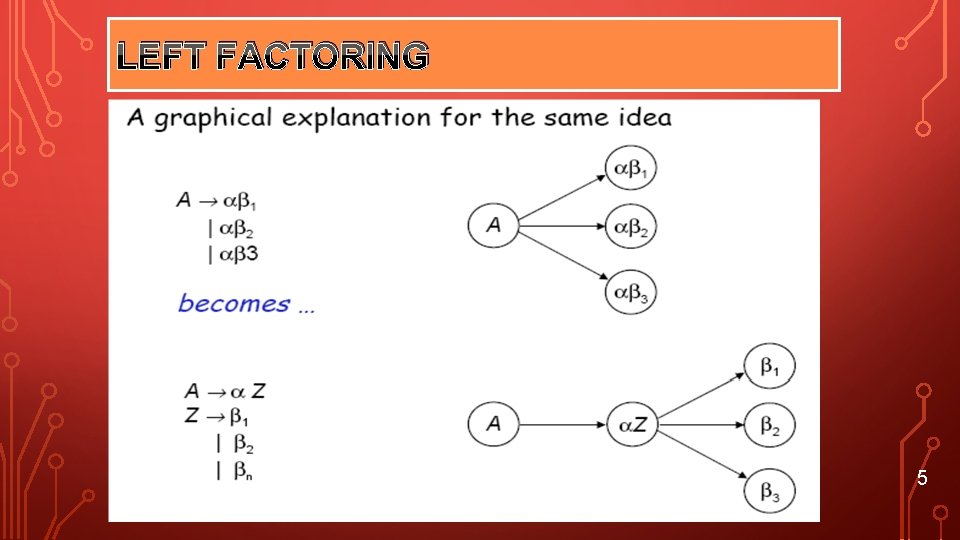
LEFT FACTORING 4

LEFT FACTORING 5

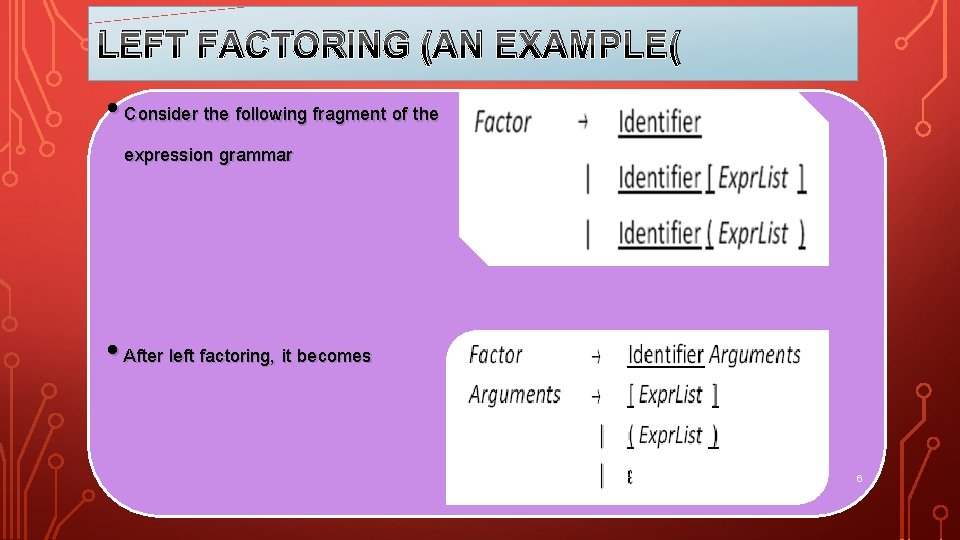
LEFT FACTORING (AN EXAMPLE( • Consider the following fragment of the expression grammar • After left factoring, it becomes 6

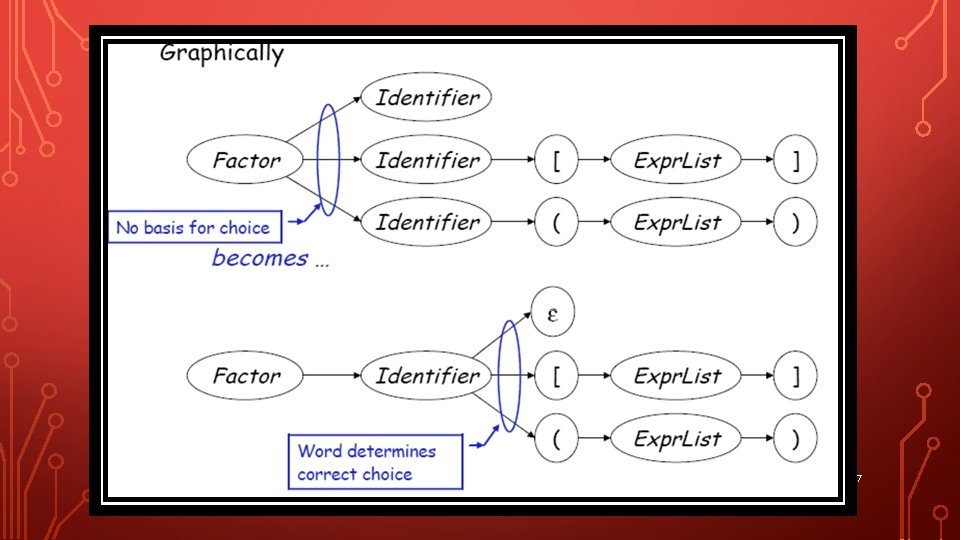
7

LEFT FACTORING (AN EXAMPLE( 8

TRY THIS • Left factoring this gramma E→T+E|T T → int | int * T | ( E( 9

LL(1) CONFLICT There are two main types of LL(1) conicts: 10

INDIRECT LEFT RECURSION & CONFLICT PROBLEM We have an indirect left-recursion around non-terminals C and D, First-First conflict between rules 1 & 2 and a First-Follow for non-terminal B (which is Nullable). 11

INDIRECT LEFT RECURSION & CONFLICT PROBLEM We can solve B's First-Follow conflict by simply making B non-Nullable. To do this, we first remove rule 4 and then for every rule that derives B, we clone the rule, but omit the B in the derivation. So that, A aa. C | aad | a. C | ad Now , Do left factoring 12

INDIRECT LEFT RECURSION & CONFLICT PROBLEM So that, A aa. C | aad | a. C | ad Now , Do left factoring A a. X X a. C |ad | C | d ( still need left factoring) So that , X a. Y | C | d Y C|d Now , we already solve the First on A and First Follow on B Next, we will solve the left recursion on C and D 13

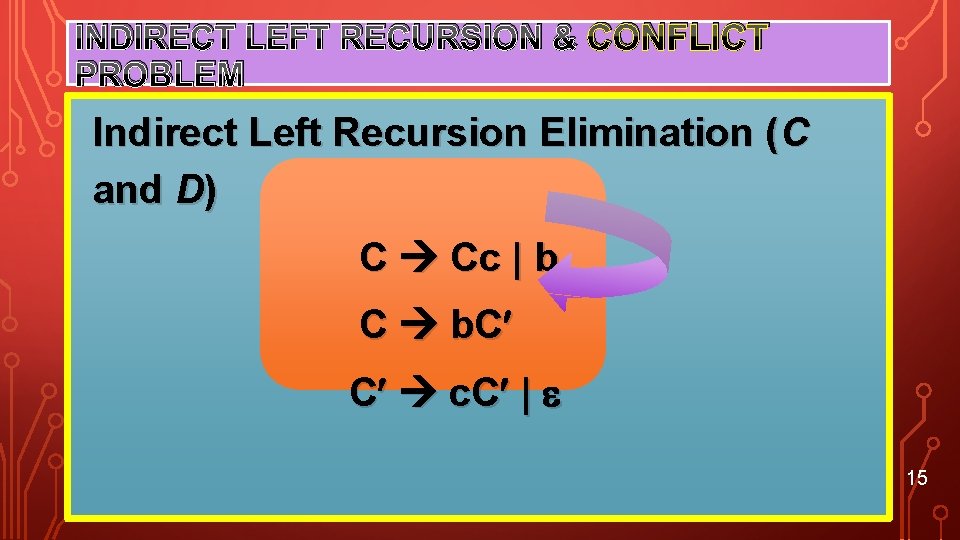
INDIRECT LEFT RECURSION & CONFLICT PROBLEM Indirect Left Recursion Elimination (C and D) We first substitute any left-non-terminal with it's possible derivation. We Remove rule 5 since it has a non-terminal at the left-most position of its RHS. We replace it with: C Cc | b 14

INDIRECT LEFT RECURSION & CONFLICT PROBLEM Indirect Left Recursion Elimination (C and D) C Cc | b C b. C C c. C | 15

INDIRECT LEFT RECURSION & CONFLICT PROBLEM Finally we get the grammar : 16

CONSTRUCTION OF A LL(1) FROM A CFG GRAMMAR v. Eliminate left recursion vleft factorization v. Add an extra start production S → S$ to the grammar v. Calculate First for every production and Follow for every nonterminal 17

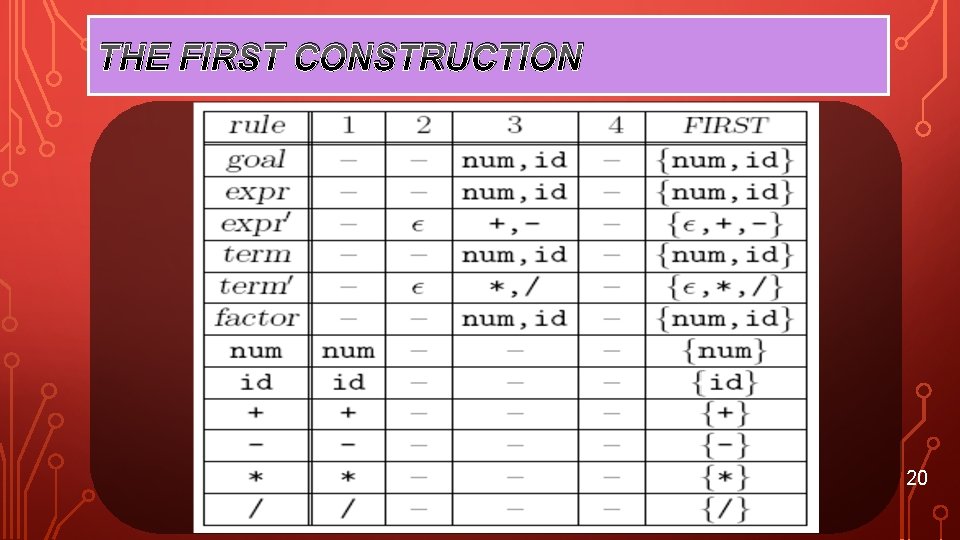
THE FIRST SET 18

EXAMPLE GRAMMAR Extra Start $ 19

THE FIRST CONSTRUCTION 20

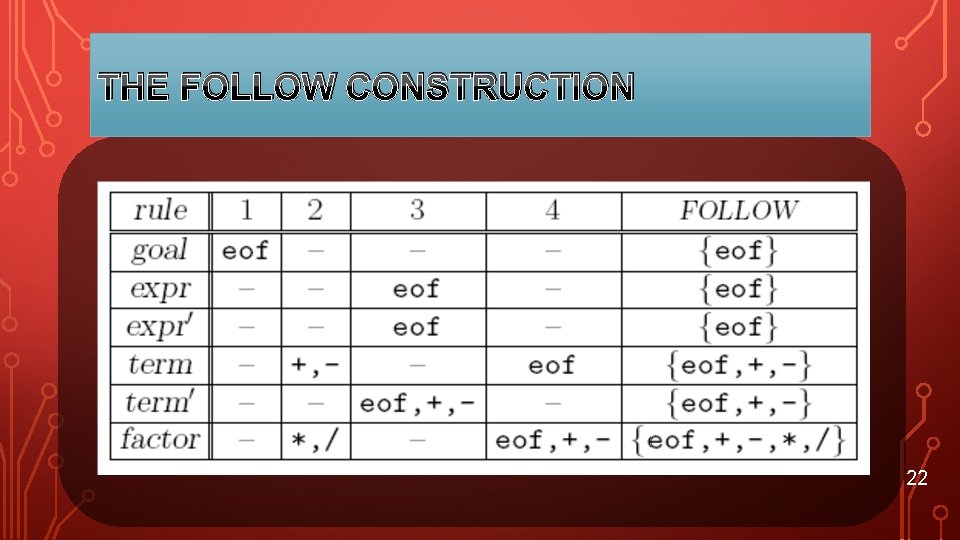
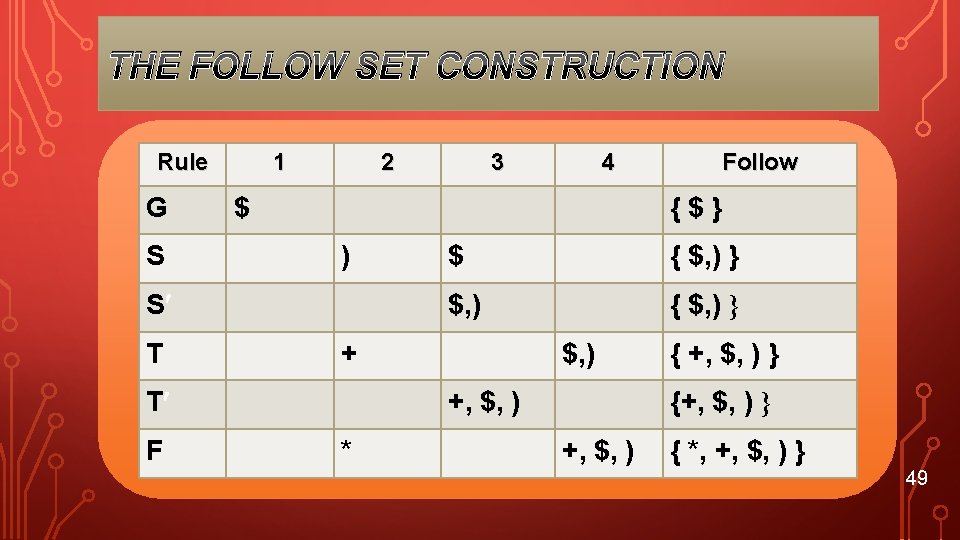
THE FOLLOW SET 21

THE FOLLOW CONSTRUCTION 22

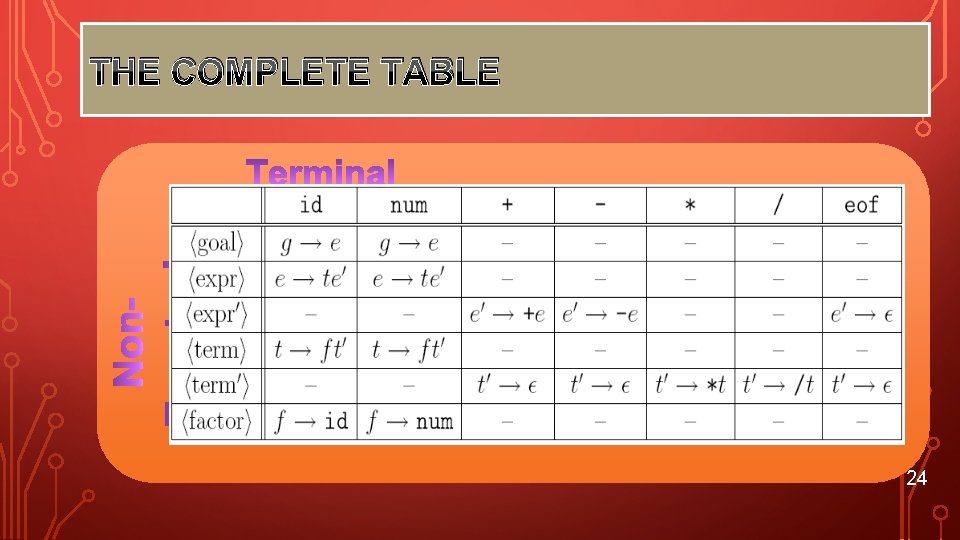
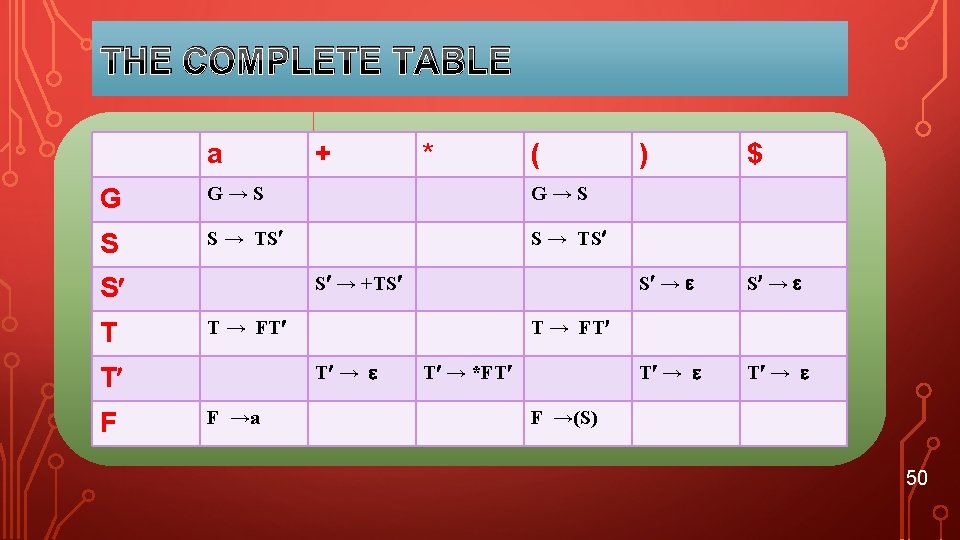
CONSTRUCTING THE LL(1) PARSING TABLE Building the complete table • Need a row for every NT & a column for every T • Need an algorithm to build the table 23

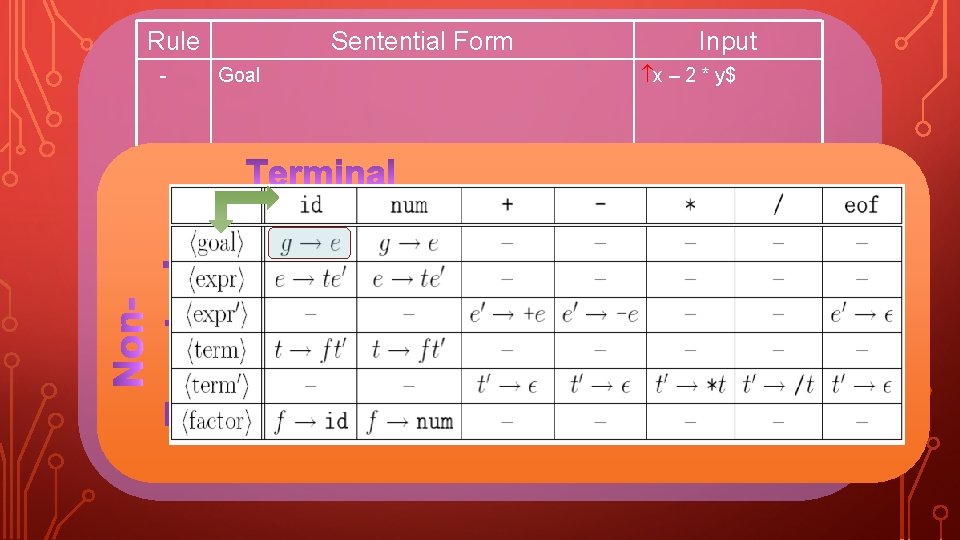
THE COMPLETE TABLE 24

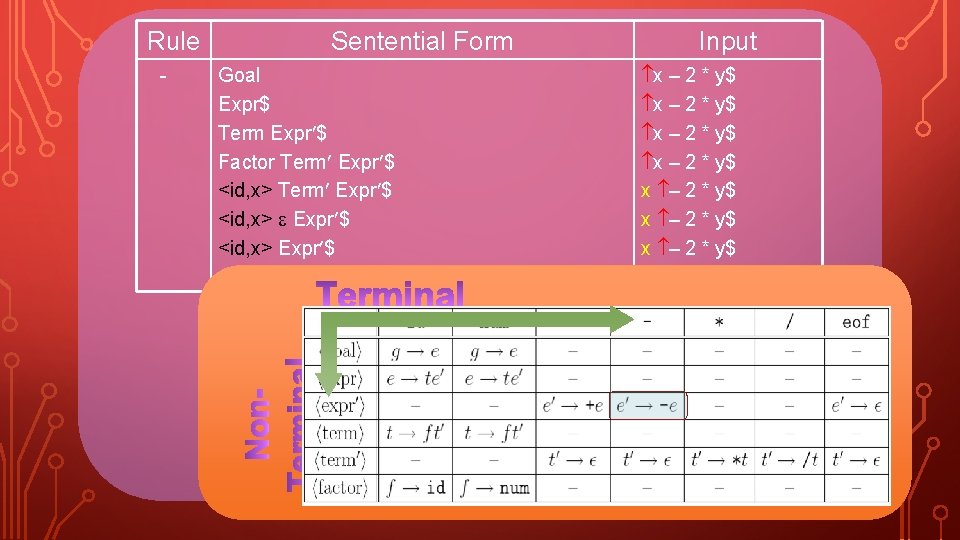
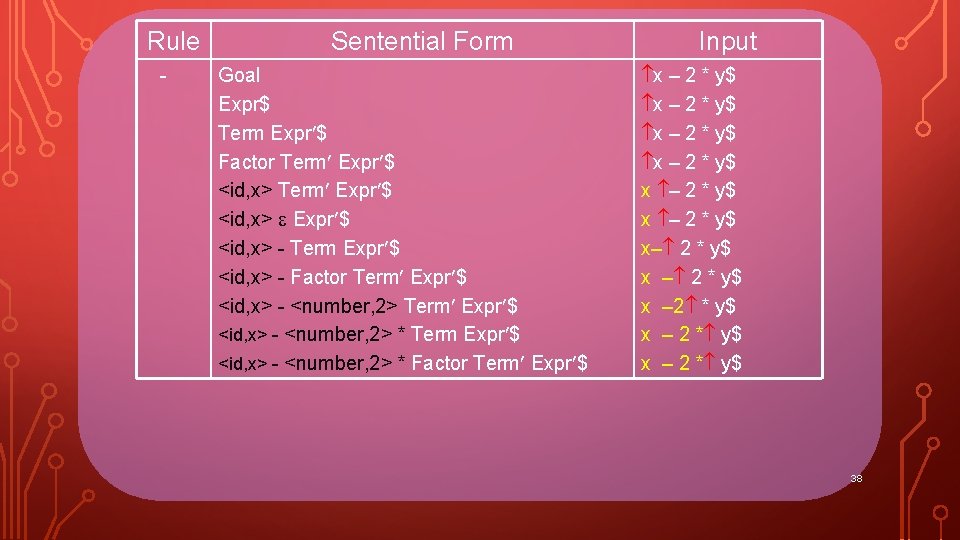
Rule - Sentential Form Goal Input x – 2 * y$ 25

Rule - Sentential Form Goal Expr$ Input x – 2 * y$ 26

Rule - Sentential Form Goal Expr$ Term Expr $ Input x – 2 * y$ 27

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ Input x – 2 * y$ 28

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> Term Expr $ Input x – 2 * y$ x – 2 * y$ 29

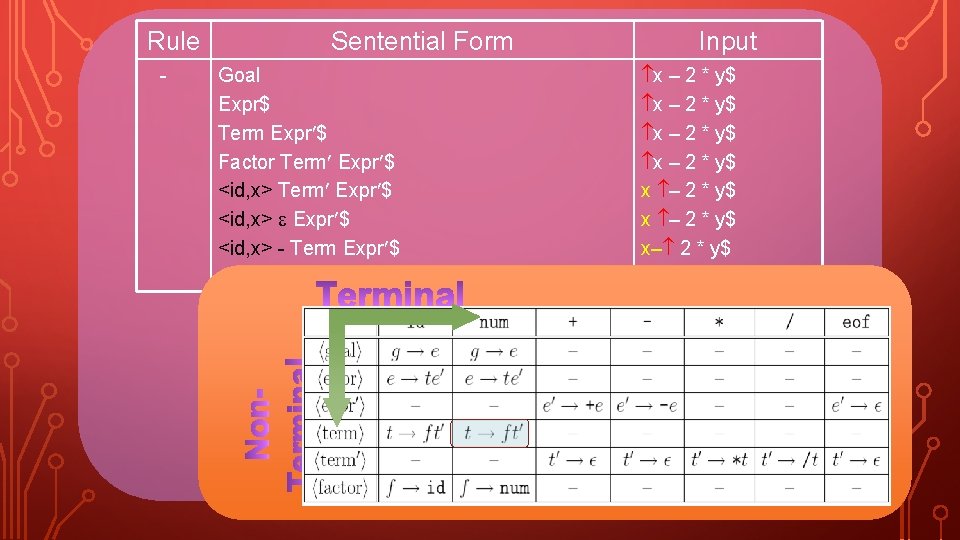
Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> Expr $ Input x – 2 * y$ x – 2 * y$ 30

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ 31

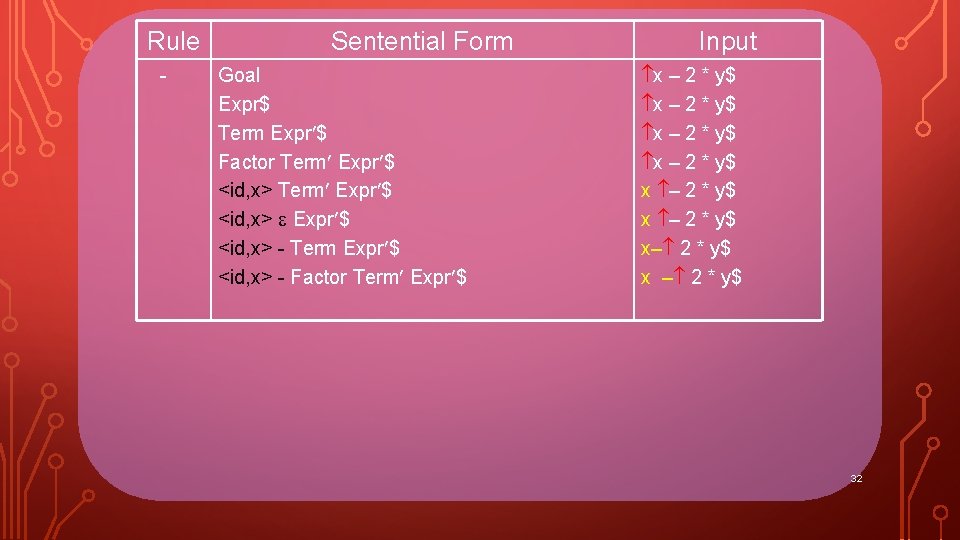
Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 32

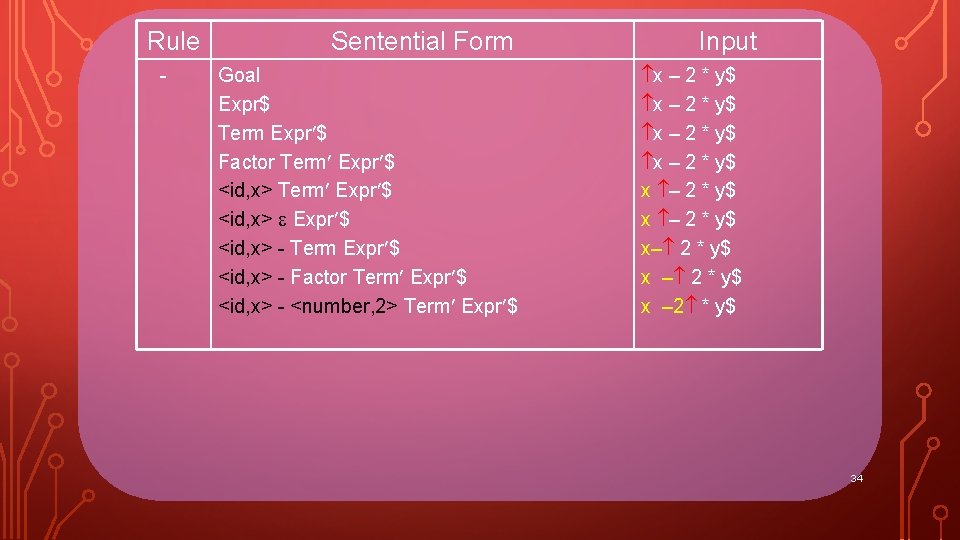
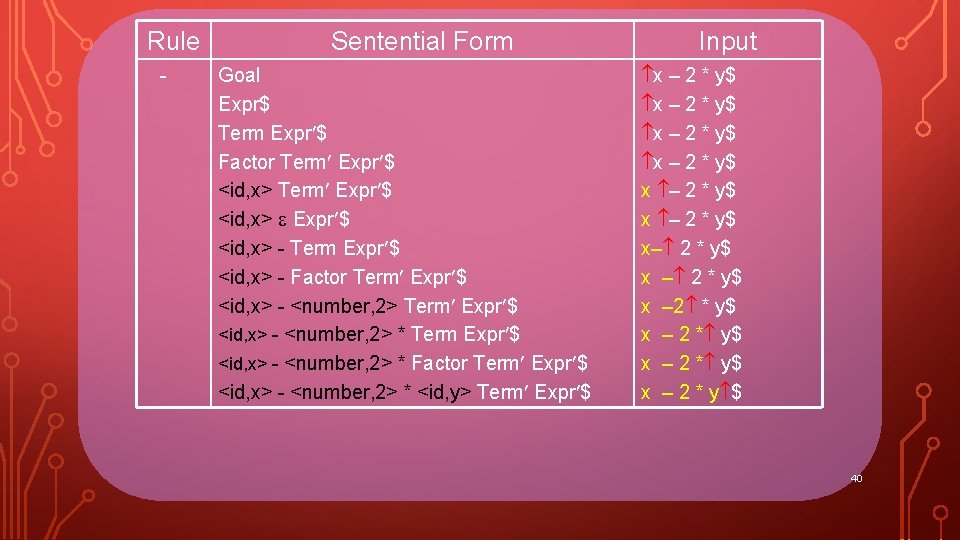
Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 33

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 34

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 35

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 36

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 37

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 38

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ 39

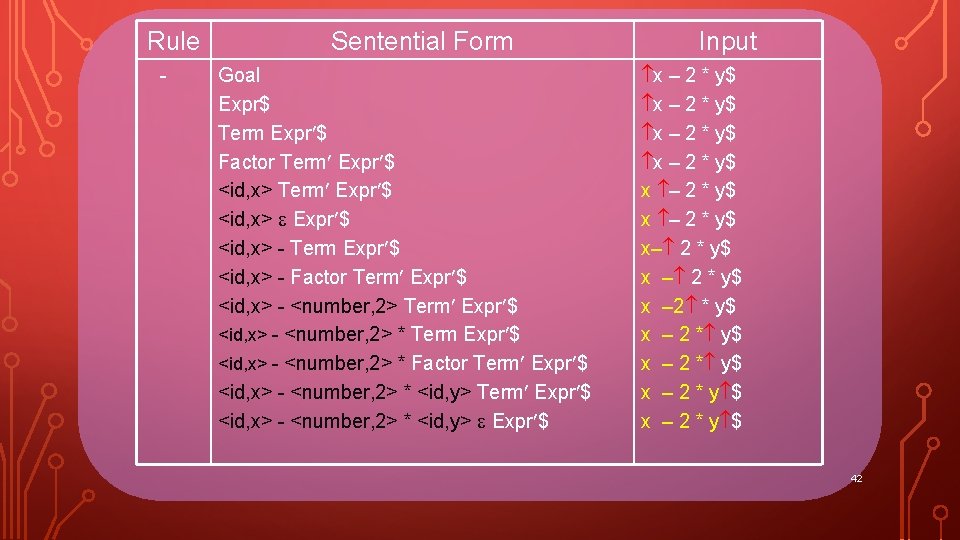
Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ <id, x> - <number, 2> * <id, y> Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ x – 2 * y $ 40

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ <id, x> - <number, 2> * <id, y> Term Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ x – 2 * y $ 41

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ <id, x> - <number, 2> * <id, y> Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ x – 2 * y $ 42

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ <id, x> - <number, 2> * <id, y> Expr $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ x – 2 * y $ 43

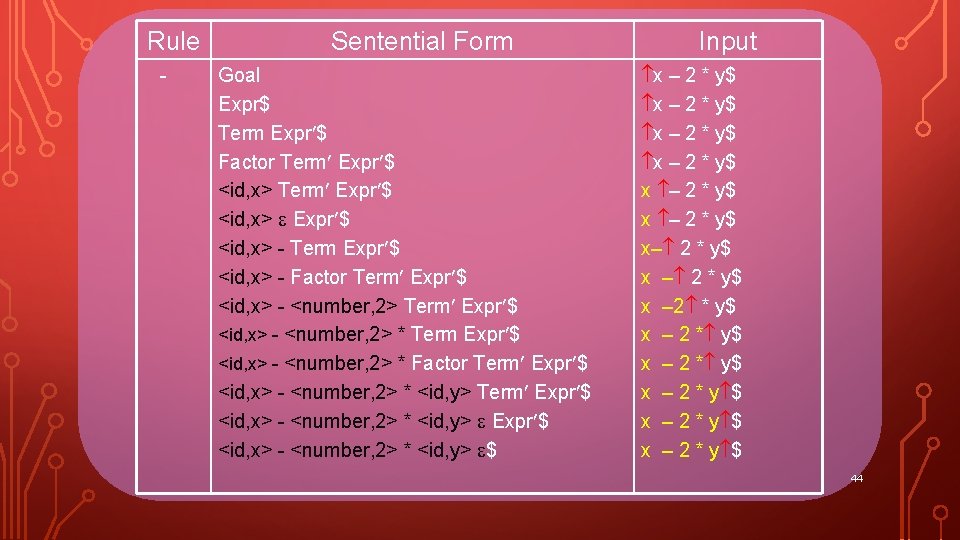
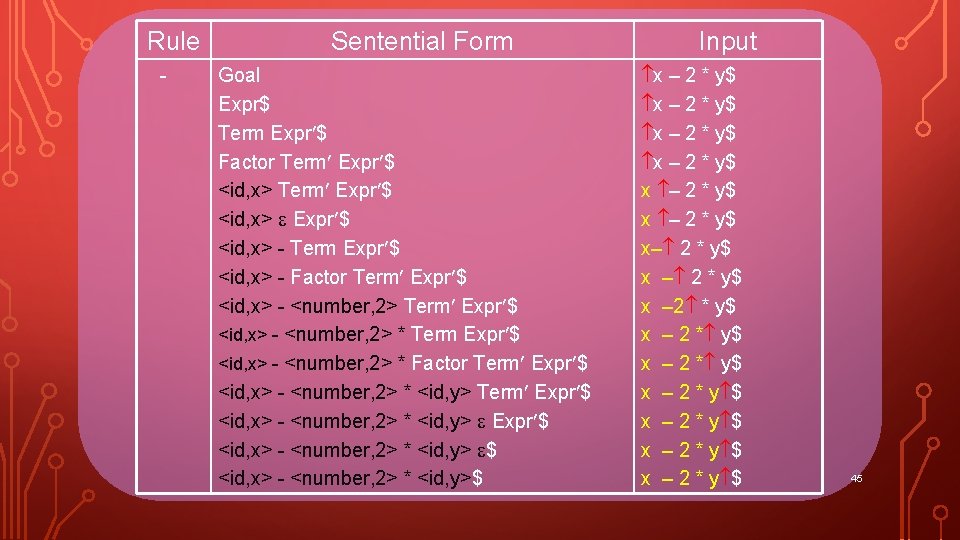
Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ <id, x> - <number, 2> * <id, y> $ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ x – 2 * y $ 44

Rule - Sentential Form Goal Expr$ Term Expr $ Factor Term Expr $ <id, x> - Term Expr $ <id, x> - Factor Term Expr $ <id, x> - <number, 2> * Factor Term Expr $ <id, x> - <number, 2> * <id, y>$ Input x – 2 * y$ x – 2 * y$ x– 2 * y$ x – 2 * y$ x – 2 * y $ 45

EXAMPLE Given a grammar : S→S+T|T T → T*F | F F →a | (S) Remove left recursive S → TS S → +TS | T → FT T → *FT | There is no left factorization. Now add an extra start : G → S$ S → TS S → +TS | T → FT T → *FT | F →a | (S) 46

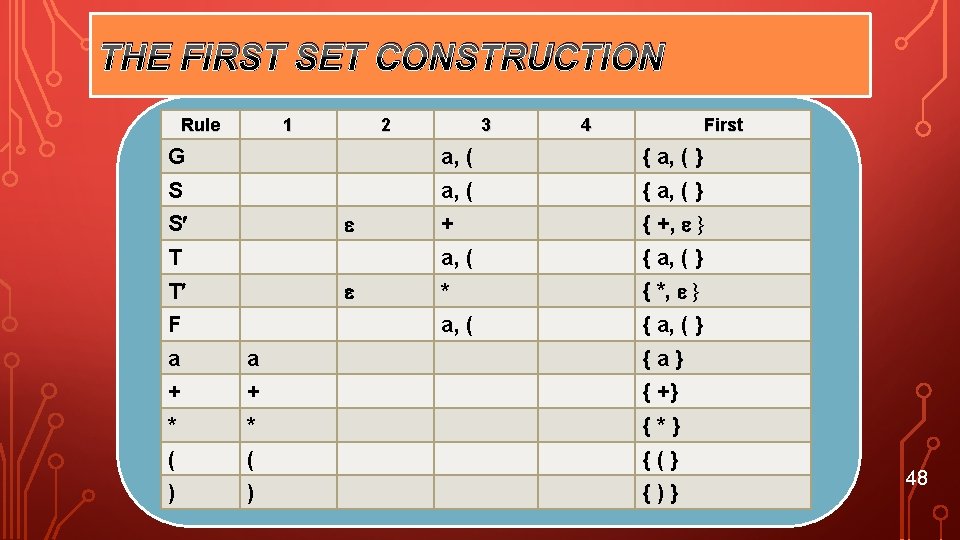
New grammar : 1 2 3 4 5 6 7 8 9 G→S S → TS S → +TS S → T → FT T → *FT T → F →a F →(S) Non-Terminal Symbol G, S, S , T, F a , +, *, (, ), $ 47

THE FIRST SET CONSTRUCTION Rule 1 2 3 4 First G a, ( { a, ( } S a, ( { a, ( } + { +, } a, ( { a, ( } * { *, } a, ( { a, ( } S T T F a a {a} + + { +} * * {*} ( ( {(} ) ) {)} 48

THE COMPLETE TABLE a + * ( G G→S S S → TS S → +TS S T T → FT F F →a $ S → T → FT T → T ) T → *FT F →(S) 50

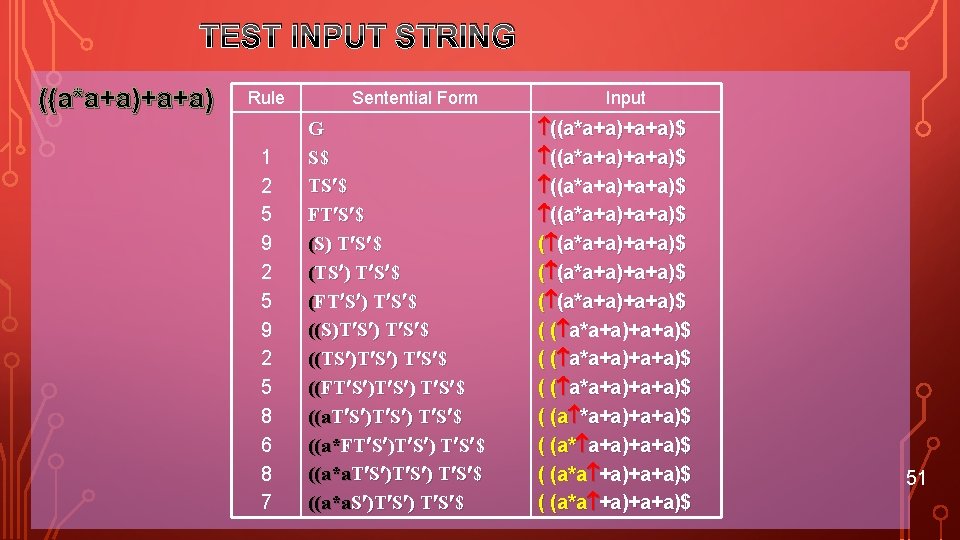
TEST INPUT STRING ((a*a+a)+a+a) Rule 1 2 5 9 2 5 8 6 8 7 Sentential Form G S$ TS $ FT S $ (S) T S $ (TS ) T S $ (FT S ) T S $ ((S)T S ) T S $ ((TS )T S ) T S $ ((FT S ) T S $ ((a*FT S )T S ) T S $ ((a*a. S )T S ) T S $ Input ((a*a+a)+a+a)$ ( (a*a+a)+a+a)$ ( ( a*a+a)+a+a)$ ( (a *a+a)+a+a)$ ( (a*a +a)+a+a)$ 51

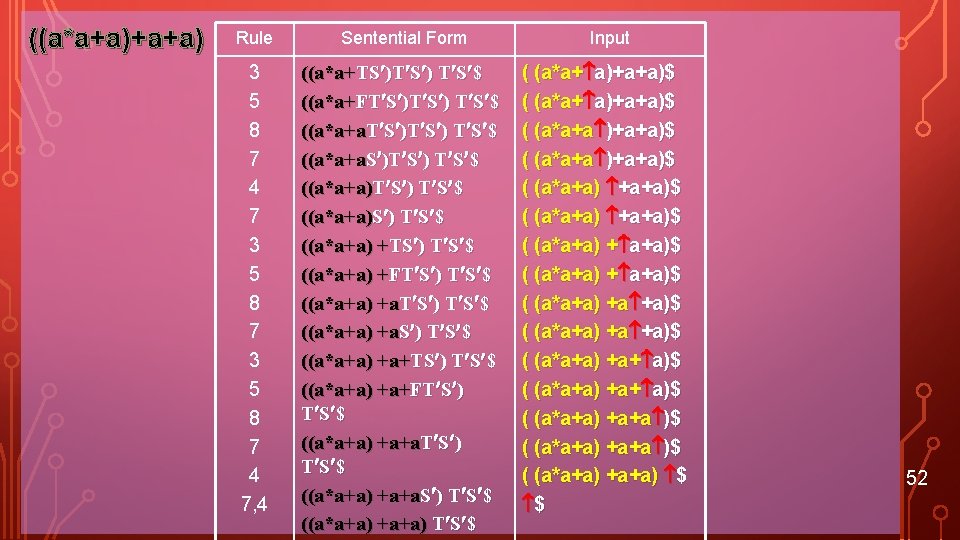
((a*a+a)+a+a) Rule Sentential Form 3 5 8 7 4 7, 4 ((a*a+TS )T S ) T S $ ((a*a+FT S )T S ) T S $ ((a*a+a)S ) T S $ ((a*a+a) +TS ) T S $ ((a*a+a) +FT S ) T S $ ((a*a+a) +a+TS ) T S $ ((a*a+a) +a+FT S ) T S $ ((a*a+a) +a+a) T S $ Input ( (a*a+ a)+a+a)$ ( (a*a+a) +a+a)$ ( (a*a+a) +a +a)$ ( (a*a+a) +a+a )$ ( (a*a+a) +a+a) $ $ 52