Criptografia e Segurana de Rede Captulo 4 Quarta

Criptografia e Segurança de Rede Capítulo 4 Quarta Edição por William Stallings Tradução por Carlos Daniel Abreu

Capítulo 4 – Corpos Finitos Na manhã seguinte, ao nascer o dia, Star entrou em casa, aparentemente ávida por uma lição. Eu disse, "Mostre oito". Ela fez uma exibição brilhante, primeiro batendo 4 -4, depois batendo rapidamente 2 -2 -2 -2, antes de entrar. É incrível como Star aprendeu a contar até oito sem dificuldade. E do seu próprio jeito descobriu que cada número pode ser dado com diferentes divisões, isso não deixa dúvida de que estava conscientemente pensando em cada número. De fato, ela fez a aritmética mental, embora não possa, como os humanos, dar nome aos números. Mas ela aprendeu a reconhecer seus nomes falados quase imediatamente e lembrar dos sons dos nomes. Star é um pássaro silvestre único que, por vontade própria, buscou a ciência dos números com ávido interesse e incrível inteligência. Living with birds, Len Howard

Introdução Ø Vamos agora apresentar Corpos Finitos Ø Do seu importante aumento na criptografia l AES, Curvas Elípticas, IDEA, Chave pública Ø Dizem a respeito de operações com números l Quando o que constitui um “número” e os tipos de operações varia consideravelmente. Ø Começaremos com conceitos de grupos, anéis e corpos de álgebra abstrata.

Grupo Ø Um conjunto de elementos ou números Ø Com algumas operações cujo resultado é também no conjunto (encerramento) Ø Devemos cumprir: l l l Lei da associatividade: (a. b). c = a. (b. c) Possui identidade: e. a = a. e = a Possui inversa a-1: a. a-1 = e Ø Se for comutativo l a. b = b. a Então forma um grupo algébrico.

Grupo Cíclico Ø definir exponenciação como aplicação repetida do operador l exemplo: a-3 = a. a. a Ø A identidade deve ser: e=a 0 Ø Um grupo é cíclico se cada elemento for uma potência de um elemento fixo. l Ex. : b = ak para algum a e todo b no grupo Ø a é dito ser um gerador do grupo

Anél Um conjunto de números Com duas operações (adição e multiplicação) que formam: Ø Um grupo comutativo com a operação de adição Ø E multiplicação: Ø Ø l l l fechamento Associatividade Leis distributivas: a(b+c) = ab + ac Se a operação de multiplicação é comutativa, isso forma um anel comutativo Ø Se a operação de multiplicação tem uma identidade e nenhum divisor por zero, isso forma um domínio integral Ø

Corpos Ø Um conjunto de números Ø Com duas operações que formam: l l l Um grupo comutativo para adição Um grupo comutativo para multiplicação (ignorando o 0) Anel Ø Tem hierarquia com mais axiomas/leis l grupo -> anel -> corpo

Aritmética Modular Definimos módulo “a mod n” como o resto quando a é dividido por n Ø Usa-se o termo congruência para: a = b mod n Ø l l Ø Quando divididos por n, a & b tem o mesmo resto Ex. : 100 = 34 mod 11 b é chamado o resíduo de a mod n l l Desde que com inteiros possamos sempre escrever: a = qn + b Normalmente escolha o menor positivo para deixar como reíduo • Ex. : 0 <= b <= n-1 l o processo é conhecido como Redução de Módulo • Ex. : -12 mod 7 = -5 mod 7 = 2 mod 7 = 9 mod 7

Divisores Ø Dizemos que b diferente de zero divide a se a=mb para algum m, onde a, b e m são inteiros Ø b divide a se não houver resto na divisão Ø A notação é b|a Ø Dizemos que b é um divisor de a Ø Ex. : todos 1, 2, 3, 4, 6, 8, 12, 24 dividem 24

Operações de Aritmética Modular Ø Usa um número finito de valores Ø Aritmética modular é quando fazemos adição & multiplicação e redução de módulo. Ø Pode-se fazer a redução a qualquer momento, Ex. : l a+b mod n = [a mod n + b mod n] mod n

Aritmética Modular Pode-se fazer com qualquer grupo de inteiros: Zn = {0, 1, … , n-1} Ø Formando um anel comutativo para adição Ø Com identidade multiplicativa Ø Repare em algumas peculiaridades Ø l l if (a+b)=(a+c) mod n then b=c mod n but if (a. b)=(a. c) mod n then b=c mod n somente se a for relativamente primo de n

Modulo 8 Addition Example + 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 1 1 2 3 4 5 6 7 0 2 2 3 4 5 6 7 0 1 3 3 4 5 6 7 0 1 2 4 4 5 6 7 0 1 2 3 5 5 6 7 0 1 2 3 4 6 6 7 0 1 2 3 4 5 7 7 0 1 2 3 4 5 6

Máximo Divisor Comum (MDC) Ø Um problema comum na teoria dos números Ø MDC (a, b) de a e b é o maior número que divide igualmente em ambos a e b l Ex. : MDC(60, 24) = 12 Ø Dizemos que dois inteiros a e b são relativamente primos se seu único fator inteiro positivo comum for 1 l l Ex. : MDC(8, 15) = 1 8 & 15 são relativamente primos

Algoritmo Euclidiano Um método eficiente para encontrar MDC(a, b) Ø Baseado no teorema: Ø l Ø MDC(a, b) = MDC(b, a mod b) O algoritmo euclidiano para encontrar MDC(a, b) é: EUCLID(a, b) 1. 2. 3. 4. 5. 6. A = a; B = b if B = 0 return R = A mod B A = B B = R goto 2 A = mdc(a, b)

Exemplo MDC(1970, 1066) 1970 = 1 x 1066 + 904 1066 = 1 x 904 + 162 904 = 5 x 162 + 94 162 = 1 x 94 + 68 94 = 1 x 68 + 26 68 = 2 x 26 + 16 26 = 1 x 16 + 10 16 = 1 x 10 + 6 10 = 1 x 6 + 4 6 = 1 x 4 + 2 4 = 2 x 2 + 0 gcd(1066, 904) gcd(904, 162) gcd(162, 94) gcd(94, 68) gcd(68, 26) gcd(26, 16) gcd(16, 10) gcd(10, 6) gcd(6, 4) gcd(4, 2) gcd(2, 0)

Corpo de Galois Ø Ø Ø Copos finitos desempenham um papel fundamental na criptografia Pode-se mostrar que a ordem de um corpo finito (número de elementos no corpo) precisa ser a potência de um primo pn Conhecidos como Corpos Finitos O corpo finito de ordem pn geralmente é escrito como GF(pn) [Galois Fields] Dois casos especiais são de interesse para nosso propósito: l GF(p) n l GF(2 )

Corpo de Galois GF(p) Ø É definido como o conjunto de inteiros juntamente com as operações aritméticas de módulo p Ø Forma um anel comutativo l Desde que tenha inverso multiplicativo Ø hence arithmetic is “well-behaved” and can do addition, subtraction, multiplication, and division without leaving the field GF(p)

GF(7) Multiplication Example 0 1 2 3 4 5 6 0 0 0 0 1 0 1 2 3 4 5 6 2 0 2 4 6 1 3 5 3 0 3 6 2 5 1 4 4 0 4 1 5 2 6 3 5 0 5 3 1 6 4 2 6 0 6 5 4 3 2 1

Finding Inverses EXTENDED EUCLID(m, b) 1. (A 1, A 2, A 3)=(1, 0, m); (B 1, B 2, B 3)=(0, 1, b) 2. if B 3 = 0 return A 3 = gcd(m, b); no inverse 3. if B 3 = 1 return B 3 = gcd(m, b); B 2 = b– 1 mod m 4. Q = A 3 div B 3 5. (T 1, T 2, T 3)=(A 1 – Q B 1, A 2 – Q B 2, A 3 – Q B 3) 6. (A 1, A 2, A 3)=(B 1, B 2, B 3) 7. (B 1, B 2, B 3)=(T 1, T 2, T 3) 8. goto 2

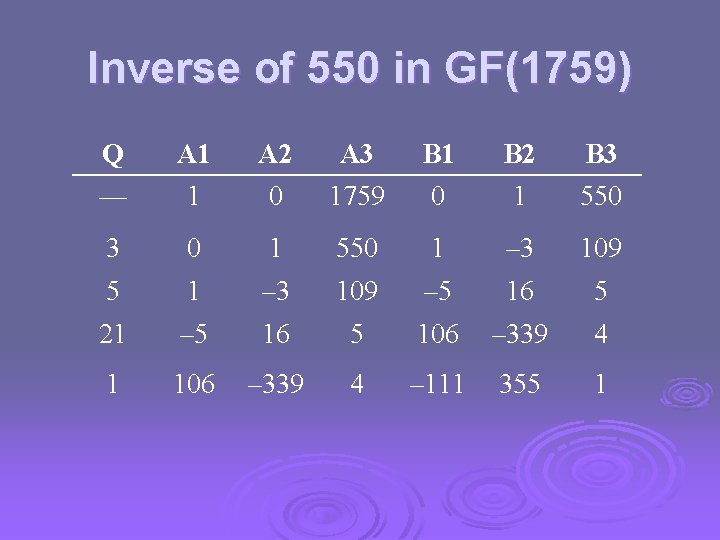
Inverse of 550 in GF(1759) Q A 1 A 2 A 3 B 1 B 2 B 3 — 1 0 1759 0 1 550 3 0 1 550 1 – 3 109 5 1 – 3 109 – 5 16 5 21 – 5 16 5 106 – 339 4 1 106 – 339 4 – 111 355 1

Aritmética Polinomial Ø Um polinômio de grau n é uma expressão na forma f(x) = anxn + an-1 xn-1 + … + a 1 x + a 0 = ∑ aixi • Normalmente não nos interessamos por avaliar um polinômio para determinado valor de x. • Que é conhecida como indeterminada Ø Podemos distinguir três classes de aritmética de polinômios: l l l Aritmética de polinômios ordinários; Aritmética de polinômios em que a aritmética sobre os coeficientes é realizada mod p Aritmética de polinômios em que os coeficientes estão em GF(p)

Aritmérica Polinomial Comum Ø Adição ou subtração dos coeficientes correspondentes Ø Multiplica-se todos os termos por cada outro Ø Ex. : let f(x) = x 3 + x 2 + 2 and g(x) = x 2 – x + 1 f(x) + g(x) = x 3 + 2 x 2 – x + 3 f(x) – g(x) = x 3 + x + 1 f(x) x g(x) = x 5 + 3 x 2 – 2 x + 2

Aritmética de Polinômios com Coeficientes em Zp Ø Se considerarmos que cada polinômio distinto é um elemento do conjunto. l Conhecido como anel polinomial Ø A divisão resultará em um quociente e um resto. Ø Porém estamos mais interessados no mod 2 l l Ex. : os coeficientes são 0 ou 1 Ex. : f(x) = x 3 + x 2 e g(x) = x 2 + x + 1 f(x) + g(x) = x 3 + x + 1 f(x) x g(x) = x 5 + x 2

Divisão Polinomial Ø Pode-se escrever qualquer polinômio da seguinte forma: l l l f(x) = q(x) g(x) + r(x) Aceitamos r(x) como sendo o resto. r(x) = f(x) mod g(x) Ø Se não tem resto dizemos que g(x) divide f(x) Ø se g(x) não tem outro divisor além dele mesmo & 1 dizemos ser um polinômio irredutível (ou primo) Ø Módulo e primo formam um corpo

Encontrando o Máximo Divisor Comum Ø Pode-se encontrar o maior divisor comum para um polinômio l Ø c(x) = MDC(a(x), b(x)) se c(x) for o polinômio de maior grau que divide os dois a(x), b(x) Pode-se usar o algoritmo euclidiano pra tal: EUCLID[a(x), b(x)] 1. A(x) = a(x); B(x) = b(x) 2. if B(x) = 0 return A(x) = mdc[a(x), b(x)] 3. R(x) = A(x) mod B(x) 4. A(x) ¨ B(x) 5. B(x) ¨ R(x) 6. goto 2

Aritmética Polinomial Modular Ø Nos concentramos em GF(2 n) l l l Polinômios com coeficientes de módulo 2 Cujo grau é inferior a n Por isso deve-se reduzir o modulo a um irredutível polinômio de grau n (para multiplicação somente) Ø Isso forma um corpo finito Ø Pode-se sempre encontrar o inverso l Pode-se usar o algoritmo do Inverso Euclidiano para encontrar.

Example GF(23)

Considerações Computacionais Ø Sejam os coeficientes 0 ou 1, pode-se representar qualquer polinômio como uma string de bits Ø Adições se tornam um XOR bit a bit Ø Multiplicação é deslocamento a esquerda seguido de um XOR l cf long-hand multiplication Ø Pode ser obtida pela aplicação repetida da Equação acrescentando resultados intermediários.

Exemplo Computacional para GF(23) temos (x 2+1) é 1012 & (x 2+x+1) é 1112 Ø Então a adição é: Ø l l Ø E a multiplicação é: l l Ø (x 2+1) + (x 2+x+1) = x 101 XOR 111 = 0102 (x+1). (x 2+1) = x. (x 2+1) + 1. (x 2+1) = x 3+x+x 2+1 = x 3+x 2+x+1 011. 101 = (101)<<1 XOR (101)<<0 = 1010 XOR 101 = 11112 Redução do modulo polinomial (get q(x) & r(x)) é l l (x 3+x 2+x+1 ) mod (x 3+x+1) = 1. (x 3+x+1) + (x 2) = x 2 1111 mod 1011 = 1111 XOR 1011 = 01002

Usando um Gerador Ø Técnica equivalente para definir um corpo finito Ø um gerador g é um elemento cujas potências geram todos os elementos diferentes de zero l Para F temos 0, g 1, …, gq-2 Ø Um elemento b contido em F é chamado de raíz do polinômio Ø Então implementa-se a multiplicação adicionando expoentes do gerador

Resumo Ø Considerações l l l Conceito de grupos, anéis, corpos Aritmética modular com inteiros Algoritmo Euclidiano para MDC Corpos Finitos GF(p) Aritmética Polinomial em geral e para GF(2 n)