Criptografia e Segurana de Redes Captulo 4 Quarta

Criptografia e Segurança de Redes Capítulo 4 Quarta Edição por William Stallings Slides por Lawrie Brown Tradução: Marcos J Pinto

Capítulo 4 – Corpos Finitos Na alvorada da manhã seguinte, Star voou porta adentro, parecendo ansiosa por uma aula. Eu disse: “Bata oito”. Ela fez uma apresentação brilhante, primeiro batendo 4 e, em seguida, lançando-me um olhar rápido, fez em 2, 2, 2, 2 antes de pegar sua castanha. É impressionante como Star aprendeu a contar até 8 sem dificuldade e, por conta própria, descobriu que cada número poderia ser dividido de diferentes formas, não deixando dúvidas de que ela estava obtendo conscientemente cada número. Na verdade, ela fazia aritmética mental, embora não tivesse a capcidade dos humanos de nomear os números. Star é ímpar como uma ave silvestre que, por vontade própria, buscou a ciência dos números com grande interesse e inteligência surpreendente. — Vivendo com pássaros, Len Howard

Introdução Ø Veremos agora os corpos Ø de crescente importância em criptografia l AES, Curvas Elipticas, IDEA, Chave Pública Ø envolve operações com “numbers” l onde o que constitui um “número” e os tipos de operações variam consideravelmente Ø Iniciamos com conceitos sobre grupos, anéis e corpos a partir da álgebra abstrata

Grupo Ø um conjunto de elementos ou “números” Ø com alguma operação cujo resultado também está presente no conjunto (fechamento) Ø obedece: l lei associativa: (a. b). c = a. (b. c) tem a identidade e: e. a = a. e = a possui inversas a-1: a. a-1 = e Ø se comutativo l a. b = b. a então forma um grupo abeliano

Grupo cíclico Ø define a exponenciação como a aplicação repetida de um operador l exemplo: a-3 = a. a. a Ø seja a identidade: e=a 0 Ø um grupo será cíclico se todos os elementos forem uma potência de algum elemento fixo l ex b = ak grupo para alguns a e todos os b do Ø diz-se que a é um gerador do grupo

Anel um conjunto de “números” com duas operações (adição e multiplicação) que formam: Ø um grupo abeliano com operação de adição Ø e multiplicação: Ø Ø l l l tem fechamento é associativo distributivo sobre a adição: a(b+c) = ab + ac Se a operação de multiplicação for comutativa, formará um anel comutativo Ø se a operação de multiplicação tiver uma identidade e nenhum divisor zero, formará um domínio integral Ø

Corpo Ø um conjunto de números Ø com duas operações que formam: l l l grupo abeliano para adição grupo abeliano para multiplicação (ignorando 0) anel Ø ter hierarquia com mais axiomas/leis l grupo -> anel -> corpo

Aritmética Modular define-se o operador módulo “a mod n” como o resto da divisão de a is por n Ø usa-se o termo congruência para: a = b mod n Ø l l Ø quando dividido por n, a & b têm o mesmo resto ex. : 100 = 34 mod 11 b é chamado de resíduo de a mod n l l como com inteiros pode-se sempre escrever: a = qn + b geralmente escolhe-se o menor resto positivo como resíduo • ex: 0 <= b <= n-1 l o processo é conhecido como redução modular • ex: -12 mod 7 = -5 mod 7 = 2 mod 7 = 9 mod 7

Divisores Ø digamos que um número diferente de zero b divida a se para algum m houver a=mb (a, b, m todos inteiros) Ø ou seja, b divide a sem resto Ø representa-se isso como b|a Ø e diz-se que b é um divisor de a Ø ex: 1, 2, 3, 4, 6, 8, 12, 24 dividem 24

Operações de Aritmética Modular Ø é a ‘aritmética do relógio' Ø emprega um número finito de valores e faz retorno circular de cada extremidade Ø há aritmética modular quando a adição & multiplicação e módulo reduzem a resposta Ø podem-se fazer reduções em qualquer ponto, ex l a+b mod n = [a mod n + b mod n] mod n

Aritmética Modular pode-se fazer aritmética modular com qualquer grupo de inteiros: Zn = {0, 1, … , n-1} Ø forma um anel comutativo para adição Ø com uma identidade multiplicativa Ø observe algumas peculiaridades Ø l l se (a+b)=(a+c) mod n então b=c mod n mas se (a. b)=(a. c) mod n então b=c mod n somente se a for relativamente primo de n

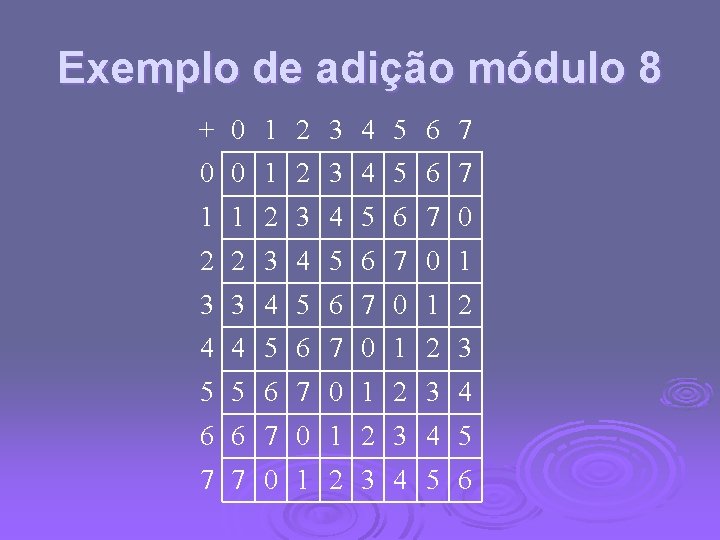
Exemplo de adição módulo 8 + 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 1 1 2 3 4 5 6 7 0 2 2 3 4 5 6 7 0 1 3 3 4 5 6 7 0 1 2 4 4 5 6 7 0 1 2 3 5 5 6 7 0 1 2 3 4 6 6 7 0 1 2 3 4 5 7 7 0 1 2 3 4 5 6

Máximo Divisor Comum (MDC) Ø um problema comum em teoria dos números Ø MDC (a, b) entre a e b é o maior divisor comum entre a e b l ex. : MDC(60, 24) = 12 Ø frequentemente não exige fatores comuns (exceto 1) e então os números são relativamente primos l l ex. : MDC(8, 15) = 1 então 8 & 15 são relativamente primos

Algoritmo Euclideano maneira eficiente de encontrar MDC(a, b) Ø emprega o teorema que: Ø l Ø MDC(a, b) = MDC(b, a mod b) Algoritmo Euclideano para calcular MDC(a, b) é: EUCLID(a, b) 1. 2. 3. 4. 5. 6. A = a; B = b if B = 0 return R = A mod B A = B B = R goto 2 A = mdc(a, b)

Exemplo: MDC(1970, 1066) 1970 = 1 x 1066 + 904 1066 = 1 x 904 + 162 904 = 5 x 162 + 94 162 = 1 x 94 + 68 94 = 1 x 68 + 26 68 = 2 x 26 + 16 26 = 1 x 16 + 10 16 = 1 x 10 + 6 10 = 1 x 6 + 4 6 = 1 x 4 + 2 4 = 2 x 2 + 0 mdc(1066, 904) mdc (904, 162) mdc (162, 94) mdc (94, 68) mdc (68, 26) mdc (26, 16) mdc (16, 10) mdc (10, 6) mdc (6, 4) mdc (4, 2) mdc (2, 0)

Corpo de Galois Ø corpos finitos são fundamentais em criptografia Ø demonstra que o número de elementos em um corpo finito deve ser uma potência de um primo pn Ø Conhecido como corpo de Galois Ø representado como GF(pn) Ø particularmente costuma usar os corpos: l l GF(p) GF(2 n)

Corpo de Galois GF(p) Ø GF(p) é o conjunto de inteiros {0, 1, … , p- 1} com operações aritméticas módulo primo p Ø formam um corpo finito l já que há inversos multiplicativos Ø então a aritmética é “bem comportada” e pode fazer adição, subtração, multiplicação e divisão sem sair do corpo GF(p)

Exemplo de multiplicação GF(7) 0 1 2 3 4 5 6 0 0 0 0 1 0 1 2 3 4 5 6 2 0 2 4 6 1 3 5 3 0 3 6 2 5 1 4 4 0 4 1 5 2 6 3 5 0 5 3 1 6 4 2 6 0 6 5 4 3 2 1

Cálculo de inversos EXTENDED EUCLID(m, b) 1. (A 1, A 2, A 3)=(1, 0, m); (B 1, B 2, B 3)=(0, 1, b) 2. if B 3 = 0 return A 3 = gcd(m, b); não há inverso 3. if B 3 = 1 return B 3 = gcd(m, b); B 2 = b– 1 mod m 4. Q = A 3 div B 3 5. (T 1, T 2, T 3)=(A 1 – Q B 1, A 2 – Q B 2, A 3 – Q B 3) 6. (A 1, A 2, A 3)=(B 1, B 2, B 3) 7. (B 1, B 2, B 3)=(T 1, T 2, T 3) 8. goto 2

Inverso de 550 em CF(1759) Q A 1 A 2 A 3 B 1 B 2 B 3 — 1 0 1759 0 1 550 3 0 1 550 1 – 3 109 5 1 – 3 109 – 5 16 5 21 – 5 16 5 106 – 339 4 1 106 – 339 4 – 111 355 1

Aritmética de polinômios Ø é possível calcular com polinômios f(x) = anxn + an-1 xn-1 + … + a 1 x + a 0 = ∑ aixi • nota: não interessa qualquer valor específico de x • que é conhecido como indeterminado Ø diversas alternativas disponíveis l l l aritmética de polinômios comum aritmética de pol com coordenadas mod p e polinômios mod m(x)

Aritmética comum entre polinômios Ø adicionar ou subtrair coeficientes correspondentes Ø multiplicar todos os termos um pelo outro Ø ex let f(x) = x 3 + x 2 + 2 and g(x) = x 2 – x + 1 f(x) + g(x) = x 3 + 2 x 2 – x + 3 f(x) – g(x) = x 3 + x + 1 f(x) x g(x) = x 5 + 3 x 2 – 2 x + 2

Aritmética de polinômios com Coeficientes de Módulo Ø ao calcular o valor de cada coeficiente, calcular modulo algum valor l forma um anel de polinômios Ø poderia ser modulo qualquer primo Ø mas estamos mais interessados em mod 2 l l ou seja, todos os coeficientes são 0 ou 1 ex. seja f(x) = x 3 + x 2 and g(x) = x 2 + x + 1 f(x) + g(x) = x 3 + x + 1 f(x) x g(x) = x 5 + x 2

Divisão de Polinômios Ø pode-se escrever qualquer polinômio na forma: l l l f(x) = q(x) g(x) + r(x) pode-se interpretar r(x) como um resto r(x) = f(x) mod g(x) Ø Se não houver resto, digamos g(x) divide f(x) Ø Se g(x) não tiver divisores além dele próprio & 1 diz-se polinômio irredutível(ou primo) Ø aritmética módulo um polinômio irredutível forma um corpo

MDC de Polinômios Ø pode-se calcular o máximo divisor comum entre polinômios l Ø c(x) = MDC(a(x), b(x)) se c(x) for o polinômio de maior grau que divide tanto a(x) como b(x) pode-se adaptar o Algoritmo de Euclides para calcular: EUCLID[a(x), b(x)] 1. A(x) = a(x); B(x) = b(x) 2. if B(x) = 0 return A(x) = gcd[a(x), b(x)] 3. R(x) = A(x) mod B(x) 4. A(x) ¨ B(x) 5. B(x) ¨ R(x) 6. goto 2

Aritmética de Polinômios Modular Ø pode-se calcular em corpo GF(2 n) l l l polinômios com coeficientes módulo 2 cujo grau seja inferior a n assim deve-se reduzir modulo um poli irredutível de grau n (somente para multiplicação) Ø forma um corpo finito Ø pode-se sempre encontrar um inverso l pode-se ampliar o algoritmo inverso de Euclides para calcular

Exemplo GF(23)

Considerações Computacionais Ø como os coeficientes são 0 ou 1, podem representar qualquer polinômio tal como uma string de 1 bit Ø a adição se torna um XOR entre strings de bit Ø a multiplicação é shift & XOR l cf long-hand multiplication Ø a redução módulo é feita substituindo-se repetidas vezes a maior potência com o resto do poli irredutível (também shift & XOR)

Exemplo computacional em CG(23) tendo (x 2+1) é 1012 & (x 2+x+1) é 1112 Ø então a adição é Ø l l Ø e a multiplicação é l l Ø (x 2+1) + (x 2+x+1) = x 101 XOR 111 = 0102 (x+1). (x 2+1) = x. (x 2+1) + 1. (x 2+1) = x 3+x+x 2+1 = x 3+x 2+x+1 011. 101 = (101)<<1 XOR (101)<<0 = 1010 XOR 101 = 11112 redução módulo de polinômios (get q(x) & r(x)) l l (x 3+x 2+x+1 ) mod (x 3+x+1) = 1. (x 3+x+1) + (x 2) = x 2 1111 mod 1011 = 1111 XOR 1011 = 01002

Uso de um Gerador Ø definição equivalente de um corpo finito Ø um generator g é um elemento cujas potências geram todos elementos diferentes de zero l em F há 0, g 1, …, gq-2 Ø pode-se criar um gerador a partir da raiz do polinômio irredutível Ø depois implementar a multiplicação adicionando-se expoentes do gerador

Sumário Ø foi abordado: l l l conceito de grupos, anéis e corpos aritmética modular com inteiros algoritmo de Euclides para MDC corpos finitos GF(p) aritmética de polinômios em geral e em GF(2 n)