CPSC 221 Algorithms and Data Structures Lecture 6

CPSC 221: Algorithms and Data Structures Lecture #6 Balancing Act Steve Wolfman 2010 W 2

Learning Goals After this unit, you should be able to: • Compare and contrast balanced/unbalanced trees. • Describe and apply the rotation algorithm to a BST to implement a balanced tree. • Recognize balanced binary search trees (among other tree types you recognize, e. g. , heaps, general binary trees, general BSTs). 2

Today’s Outline • Addressing one of our problems • Single and Double Rotations • AVL Tree Implementation

Beauty is Only (log n) Deep • Binary Search Trees are fast if they’re shallow: – perfectly complete except the one level fringe (like a heap) – anything else? What matters here? Problems occur when one branch is much longer than the other!

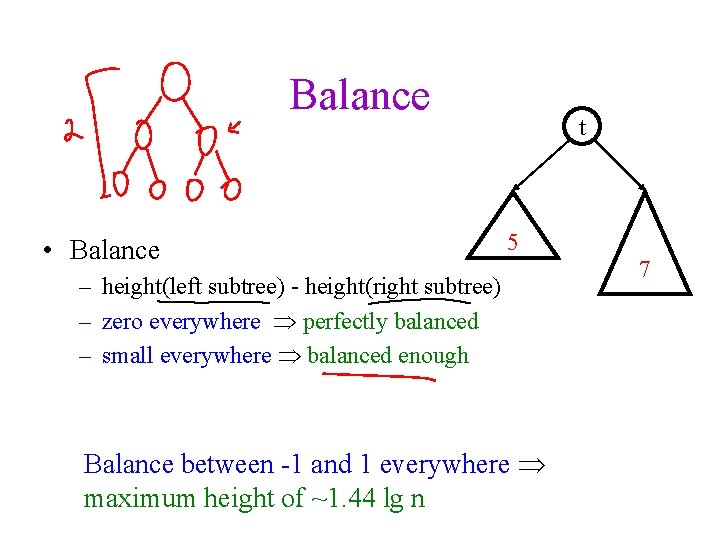
Balance • Balance t 5 – height(left subtree) - height(right subtree) – zero everywhere perfectly balanced – small everywhere balanced enough Balance between -1 and 1 everywhere maximum height of ~1. 44 lg n 7

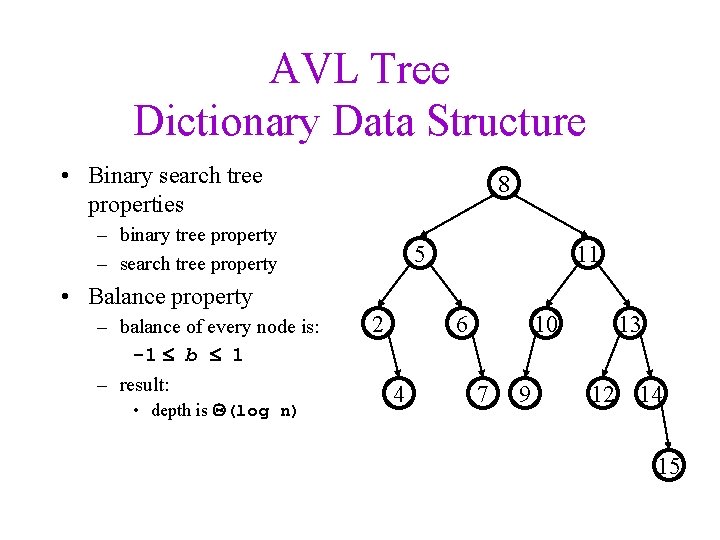
AVL Tree Dictionary Data Structure • Binary search tree properties 8 – binary tree property – search tree property 5 11 • Balance property – balance of every node is: -1 b 1 – result: • depth is (log n) 2 6 4 10 7 9 13 12 14 15

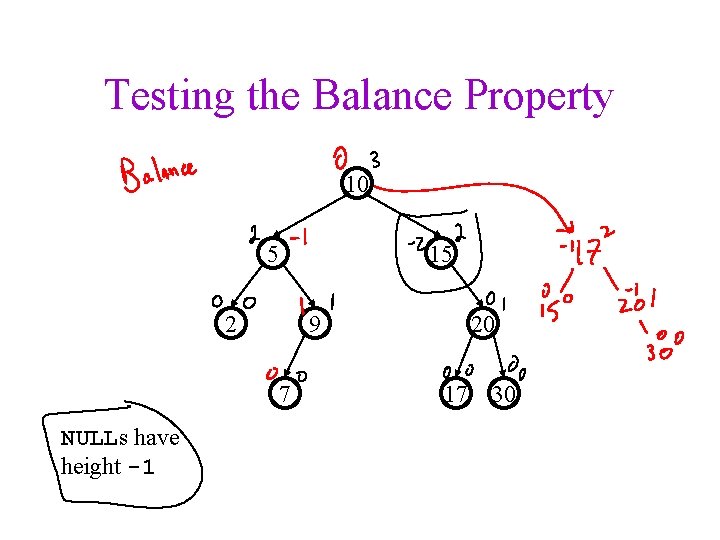
Testing the Balance Property 10 5 15 2 9 7 NULLs have height -1 20 17 30

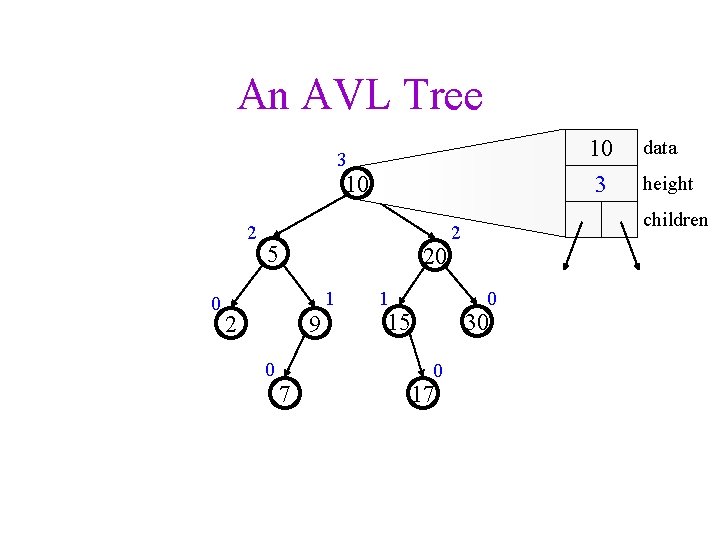
An AVL Tree 10 3 3 10 2 0 5 20 1 2 9 0 7 1 30 0 17 height children 2 0 15 data

Today’s Outline • Addressing one of our problems • Single and Double Rotations • AVL Tree Implementation

But, How Do We Stay Balanced? • Need: three volunteers proud of their very diverse height.

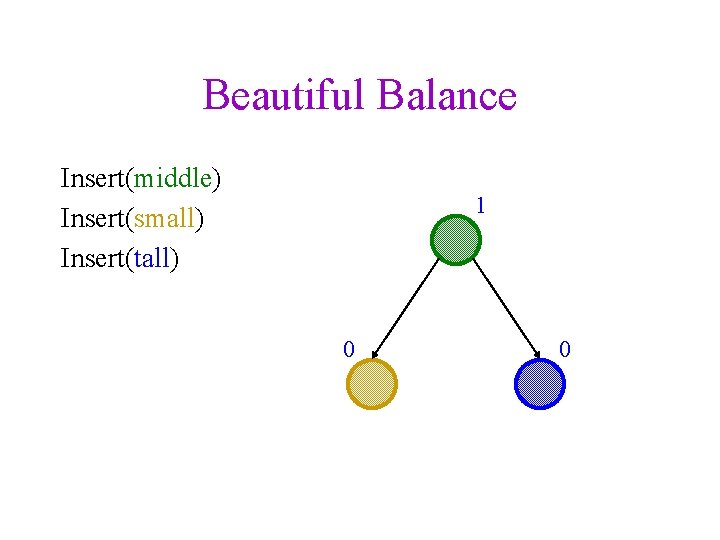
Beautiful Balance Insert(middle) Insert(small) Insert(tall) 1 0 0

Bad Case #1 Insert(small) Insert(middle) Insert(tall) 2 1 0

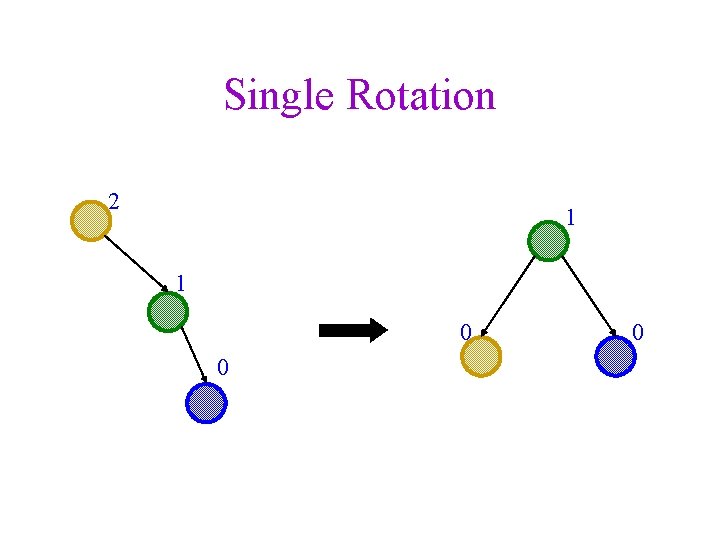
Single Rotation 2 1 1 0 0 0

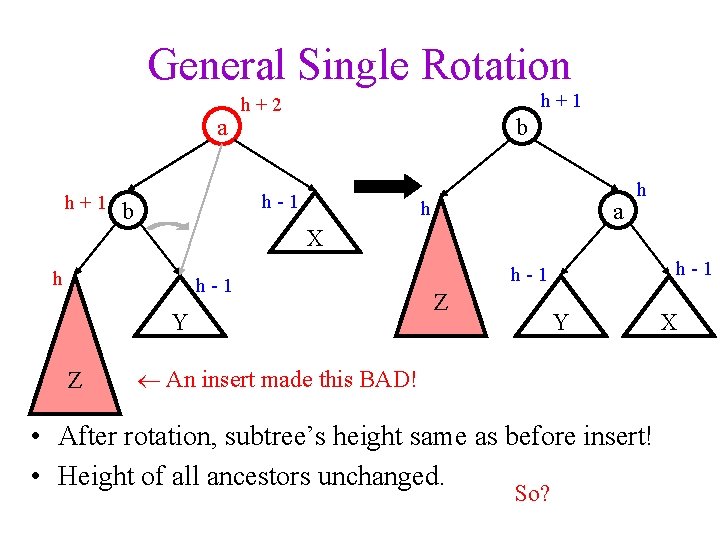
General Single Rotation a h+1 h+2 b h-1 b h a h X h h-1 Y Z h-1 Z Y An insert made this BAD! • After rotation, subtree’s height same as before insert! • Height of all ancestors unchanged. So? X

Bad Case #2 Insert(small) Insert(tall) Insert(middle) 2 1 0

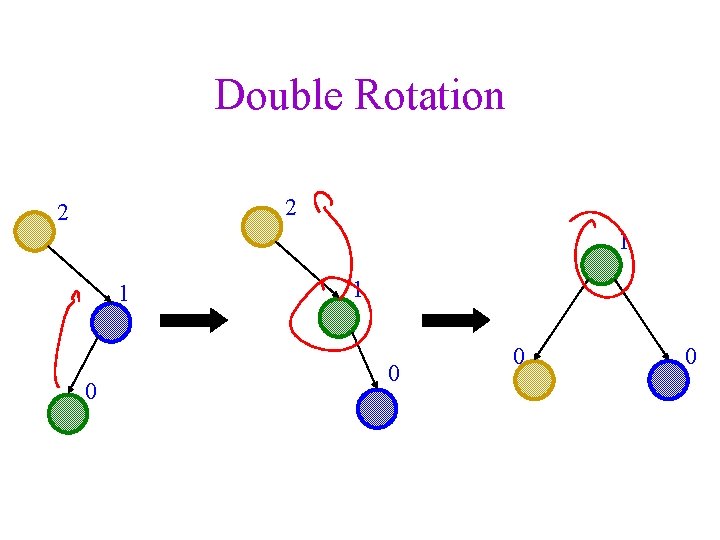
Double Rotation 2 2 1 1 0 0 0

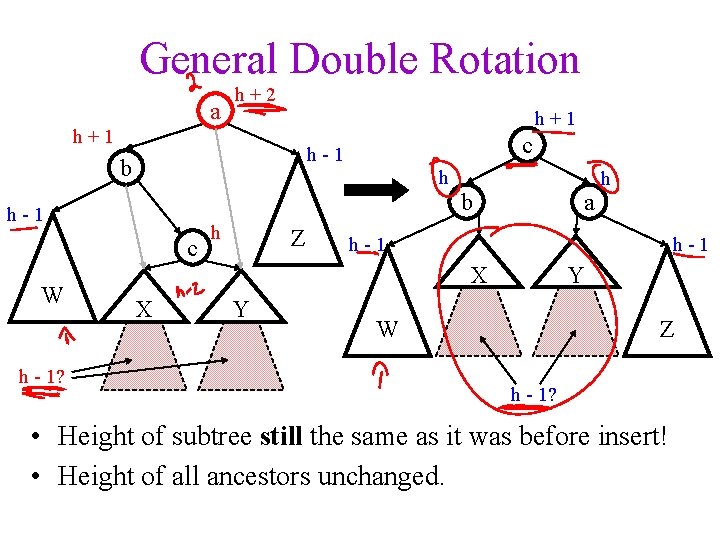
General Double Rotation a h+2 h+1 b h-1 c W h - 1? c h-1 h Z a h-1 X X Y h Y W Z h - 1? • Height of subtree still the same as it was before insert! • Height of all ancestors unchanged.

Today’s Outline • Addressing one of our problems • Single and Double Rotations • AVL Tree Implementation

Insert Algorithm • • Find spot for value Hang new node Search back up for imbalance If there is an imbalance: case #1: Perform single rotation and exit case #2: Perform double rotation and exit Mirrored cases also possible

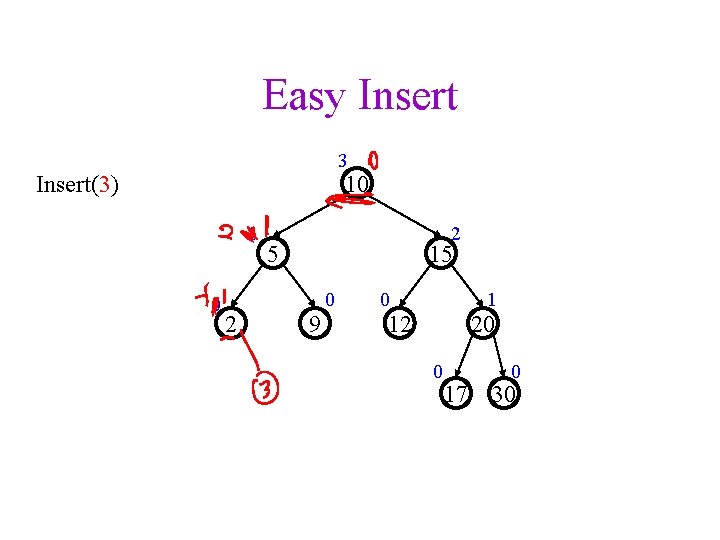
Easy Insert 3 10 Insert(3) 1 0 2 2 5 15 9 0 0 1 12 20 0 17 0 30

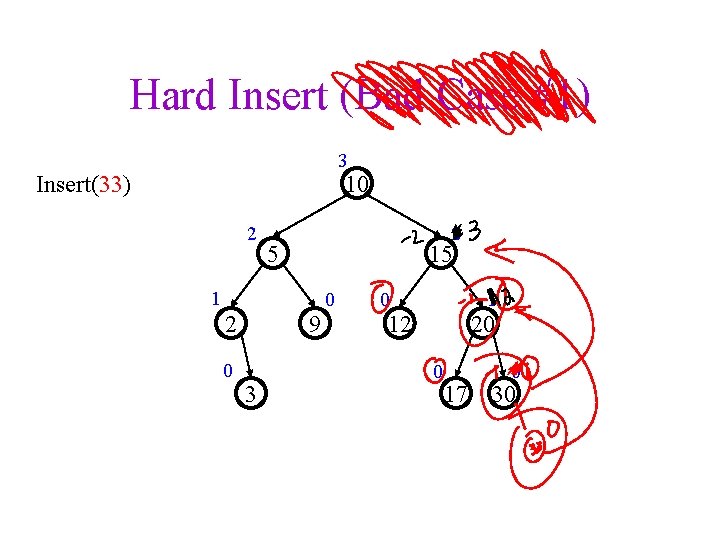
Hard Insert (Bad Case #1) 3 10 Insert(33) 2 2 5 15 1 2 0 9 3 0 0 1 12 20 0 17 0 30

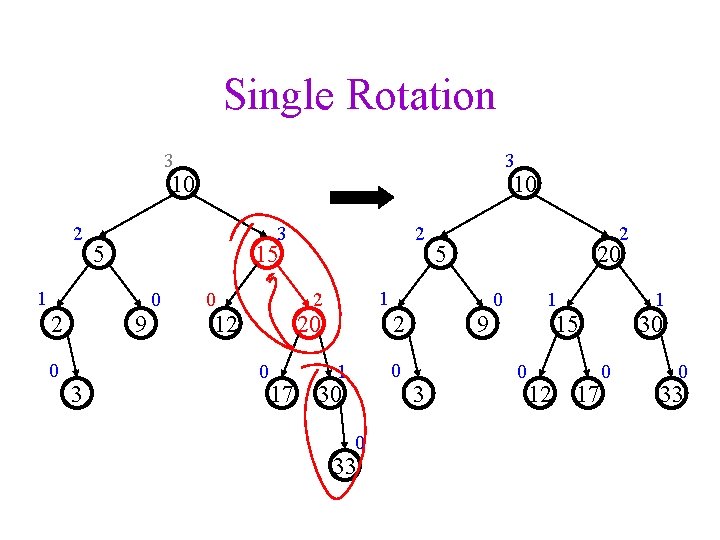
Single Rotation 3 3 10 2 3 5 0 9 3 2 15 1 2 10 0 0 20 0 17 5 20 1 2 12 2 2 0 1 30 0 33 9 3 0 1 1 15 0 12 17 30 0 0 33

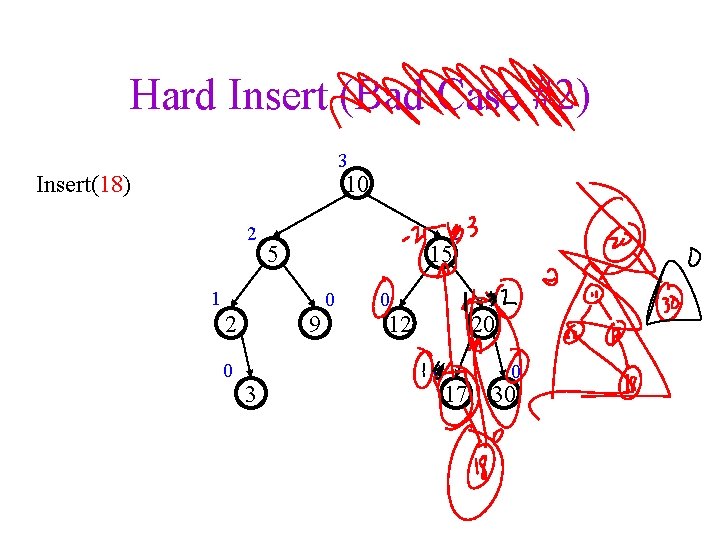
Hard Insert (Bad Case #2) 3 10 Insert(18) 2 2 5 15 1 2 0 9 3 0 0 1 12 20 0 17 0 30

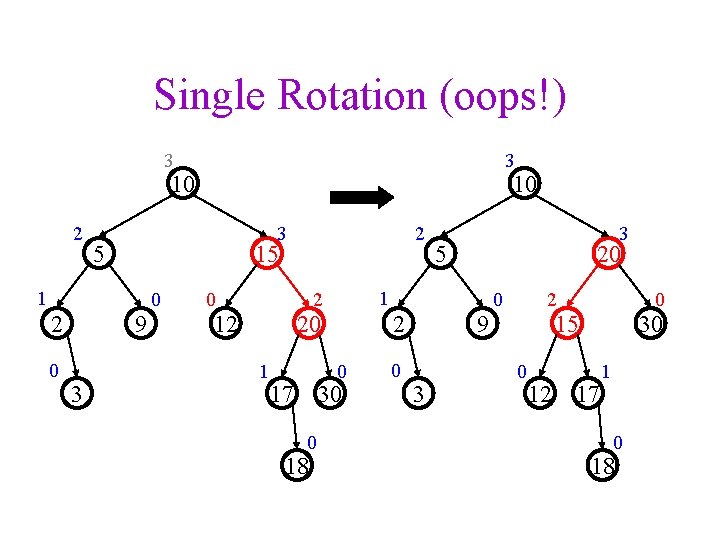
Single Rotation (oops!) 3 3 10 2 3 5 0 9 3 2 15 1 2 10 0 0 20 1 2 0 17 30 0 18 5 20 1 2 12 3 0 9 3 0 2 0 15 0 12 30 17 1 0 18

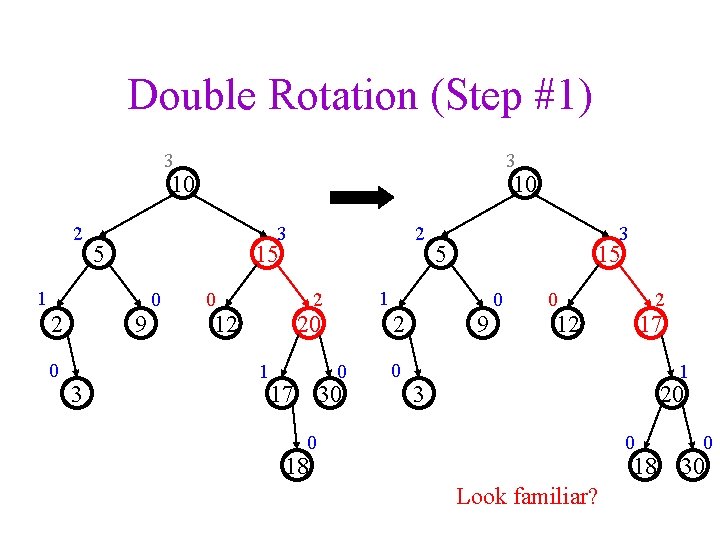
Double Rotation (Step #1) 3 3 10 2 3 5 0 9 3 2 15 1 2 10 0 0 20 1 2 0 17 5 15 1 2 12 3 30 0 9 0 0 2 12 17 1 3 20 0 0 18 18 Look familiar? 0 30

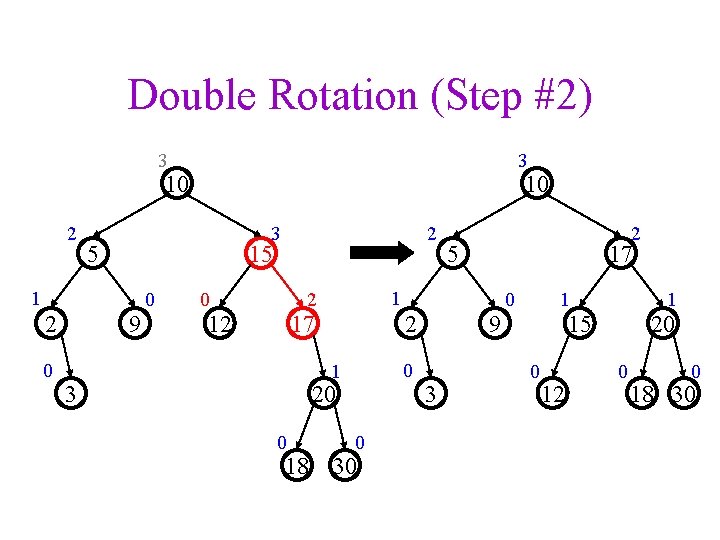
Double Rotation (Step #2) 3 3 10 2 3 5 0 2 15 1 2 10 9 0 0 17 2 0 1 3 20 0 18 5 17 1 2 12 2 0 30 9 3 0 1 1 15 0 12 20 0 0 18 30

AVL Algorithm Revisited • Recursive • Iterative 1. Search downward for spot 2. Insert node 3. Unwind stack, correcting heights a. If imbalance #1, single rotate b. If imbalance #2, double rotate 1. Search downward for spot, stacking parent nodes 2. Insert node 3. Unwind stack, correcting heights a. If imbalance #1, single rotate and exit b. If imbalance #2, double rotate and exit (Parent pointers make iterative version easier. )

Single Rotation Code void Rotate. Left(Node *& root) { Node * temp = root->right; root->right = temp->left; X temp->left = root; root->height = max(height(root->right), height(root->left)) + 1; temp->height = max(height(temp->right), height(temp->left) + 1; root = temp; } root temp Y Z (The “height” function returns -1 for a NULL subtree or the “height” field of a non-NULL subtree. ) Notice that root is a reference parameter. MUST be the “correct” pointer.

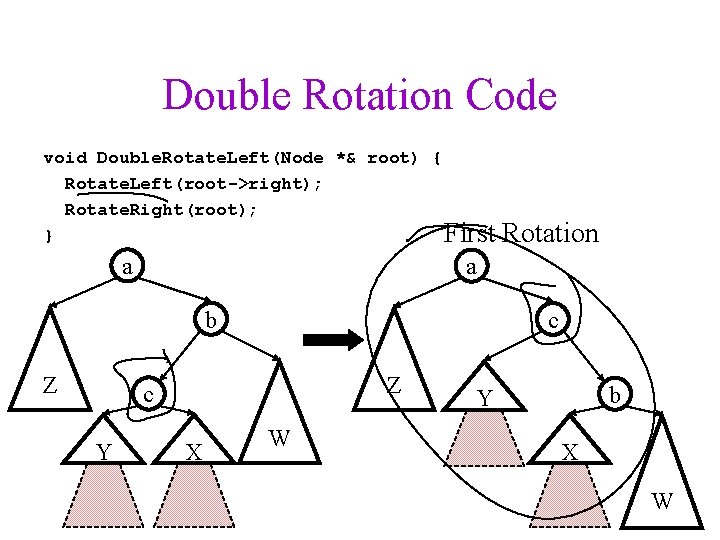
Double Rotation Code void Double. Rotate. Left(Node *& root) { Rotate. Left(root->right); Rotate. Right(root); } First a a b Z c Y Rotation X W b Y X W

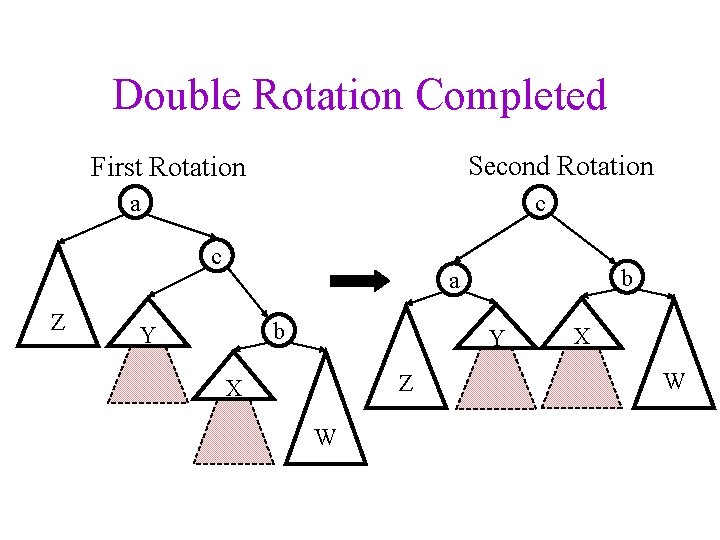
Double Rotation Completed Second Rotation First Rotation c a c Z b a b Y Y Z X W

Coming Up • Another approach to balancing, which leads to… • Huge Search Tree Data Structure • OR: A totally different approach to fast dictionaries: making a hash of your keys.