CPSC 221 Data Structures Lecture 23 Counting Steve

Learning Goals After this unit, you should be able to: • Apply counting principles

Counting: Motivation • This is sometimes really useful, e. g. : – How many

Counting: Warning • However, once you get beyond basic problems, it can be very

Outline • • • Case-Splitting, Decision Trees “Addition Rule” Deconstructed “Multiplication Rule” Deconstructed Alan’s

Counting • The basic problem is to count how many items are in some

Basic Technique: Case Splitting • This is the most fundamental way to break a

Case Splitting Example • What’s the population of Canada?

Case Splitting Example • What’s the population of Canada? – – – What’s the

Other case splits are possible • What’s the population of Canada? – How many

“Addition Rule” Demystified • From Epp: “Suppose a finite set A equals the union

Addition Principle (Sum Rule) If X 1, X 2, …, Xt are pairwise disjoint

Case Splitting Error: Missing Cases • What’s the population of Canada? – Liberals –

Case Splitting Error: Overlap • What’s the population of Canada? – Francophone Canadians –

Cases can be split into sub-cases • What’s the population of Canada? – What’s

Decision Trees • When you split cases into subcases, it’s often nice to draw

Case Splitting Example • How many different min-heaps are possible with the numbers 1,

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the

Case Splitting: Splitting into Sub-Cases • How many have 1 at the root, 2

Multiplication! E. g. : suppose there are 30 NHL teams, each with 23 players.

Multiplication! If some case split results in a bunch of identical-sized sub-cases, the total

Multiplication Principle (Product Rule) If an operation consists of t steps and: Step 1

Permutations and Factorial The number of ways to arrange n distinct items in a

Permutations P(n, r) • What if we only want permutations of r elements out

Permutations P(n, r) Note the underline below the r. This notation is due to

Permutations P(n, r) You can understand this by canceling out terms. But there’s an

P(n, r)=n!/(n-r)! Intuition • How many ways to line up 20 people? • If

P(n, r)=n!/(n-r)! Intuition • How many ways to line up n people? • If

Alan’s “Division Rule” • If the things you are trying to count are really

Division Rule and Combinations • Suppose the 5 prizes are identical, so I don’t

Division Rule and Combinations • Suppose the r prizes are identical, so I don’t

Combinations C(n, r) • These are called “combinations” – the number of ways of

Binomial Coefficients? • If I compute (x+1)^n, what’s the coefficient of x^r • (x+1)(x+1)…(x+1)

Dealing with Overlapping Cases • Suppose we try to compute population of the Americas

Dealing with Overlapping Cases • This goes by the fancy name “inclusion-exclusion principle”, but

Old Counting Slides These are for practice and your reference. (BTW, on my computer,

Today’s Outline • • Multiplication Principle Addition Principle Inclusion/Exclusion Principle Combinations and Permutations –

In CS, we often encounter situations where we want to count the number of

Suppose that the customers of a bank are asked to use 3 -digit PINs

(b) Model the problem using a tree diagram.

Example: Use the multiplication principle to prove that the number of subsets of a

Example: Suppose a programming language requires you to define variable names (identifiers) using exactly

Example: Let X be a set with n elements. How many ordered pairs (A,

Example: Suppose a user is asked to create an alphanumeric password consisting of at

Back-of-the-envelope calculation. For the previous example, roughly how long would it take for a

Inclusion-Exclusion Principle If an object can be found in 2 or more sets at

Example: How many 8 -bit strings either start with “ 1” or end with

Permutations & Combinations How many different outcomes are there if you choose r balls

Example: r = 3 Barrel = {A, B, C, D} Repetition not OK e.

(1) r-Permutations (Order matters, and repetition is not allowed. ) An r-permutation of n

Example 1: In how many ways can 5 electoral candidates finish in an election,

Example 3: Suppose an operating system has a queue of 3 low priority and

(2) r-Combinations (Order doesn’t matter, and repetition is not allowed. ) An r-combination of

(3) r-Permutations with Repetition (Generalized r. Permutations) Here, order matters, and repetition is allowed.

(4) r-Combinations with Repetition (Generalized r. Combinations) Here, order doesn’t matter, and repetition is

Example 8: If a donut shop sells 3 kinds of donuts: plain, glazed, and

Summary of Formulas Order Matters & Repetition is Order does not Matter & not

Permutations of Indistinguishable Objects Multinomial Theorem: The number of different permutations of n objects

Example 9: How many strings can be made by reordering the letters PEPPER?

Theorem: The number of ways to place n distinguishable objects into r distinguishable boxes

Slides: 98

Download presentation

CPSC 221: Data Structures Lecture #23 Counting Steve Wolfman (stolen from Alan J. Hu who stole some from me which I stole from Kim Voll) 2011 W 2

Learning Goals After this unit, you should be able to: • Apply counting principles to determine the number of arrangements or orderings of discrete objects, with or without repetition, and given various constraints. • Use appropriate mathematical constructs to express a counting problem (e. g. counting passwords with various restrictions placed on the characters within). • Identify problems that can be expressed and solved as a combination of smaller sub problems. When necessary, use decision trees to model more complex counting problems. 2

Counting: Motivation • This is sometimes really useful, e. g. : – How many possible passwords, encryption keys, etc. – How many possible legal inputs, how many possible data structure configurations, how many paths through a network, etc. – Crucial step in computing probabilities. • Sometimes fun – like a puzzle or game.

Counting: Warning • However, once you get beyond basic problems, it can be very subtle, and there are no simple tricks that always work. Sometimes, you just have to think really, really hard and really carefully! • Epp textbook is pretty good. Must read on your own. (3 rd ed 6. 1 -6. 5, 4 th ed. 9. 1 -9. 6) • Old slides follow textbook presentation closely. • I am going to try to de-mystify some of the formulas.

Outline • • • Case-Splitting, Decision Trees “Addition Rule” Deconstructed “Multiplication Rule” Deconstructed Alan’s “Division Rule” Permutation and Combination Formulas Dealing with Overlapping Cases: Inclusion-Exclusion

Counting • The basic problem is to count how many items are in some set, which might be specified in a nonobvious way. • E. g. , how many different min-heaps are possible with the numbers 1, …, 7? • How many poker hands beat a pair of kings? • Etc.

Basic Technique: Case Splitting • This is the most fundamental way to break a problem down into simpler parts. – The cases must be disjoint (no overlap). (We’ll handle overlap later. ) – Combined, the cases must cover all possibilities. • Count each case separately, then add them all up. • Whenever you are totally lost, always fall back to case-splitting. Point of interest: disjoint but covering sets form a partition.

Case Splitting Example • What’s the population of Canada?

Case Splitting Example • What’s the population of Canada? – – – What’s the population of BC? What’s the population of AB? What’s the population of SK? What’s the population of MB? etc. • Add them all up!

Other case splits are possible • What’s the population of Canada? – How many men in Canada? – How many women in Canada? • Add them all up!

“Addition Rule” Demystified • From Epp: “Suppose a finite set A equals the union of k distinct mutually disjoint subsets A 1, A 2, …, Ak. Then N(A) = N(A 1)+N(A 2)+…+N(Ak). ”

Addition Principle (Sum Rule) If X 1, X 2, …, Xt are pairwise disjoint sets (i. e. , Xi ∩ Xj = ∅ ∀i ∀j s. t. i, j∈{1, 2, …, t }, i ≠ j), then the number of ways to select an element from any of X 1 or X 2 or … or Xt is: | X 1 | + | X 2 | + … + | X t |

Case Splitting Error: Missing Cases • What’s the population of Canada? – Liberals – Conservatives – NDPs • Add them all up! • If we miss any cases (e. g. , Greens, Rhinoceros Party, Marijuana Party, people without political parties, etc. ), we’ll undercount.

Case Splitting Error: Overlap • What’s the population of Canada? – Francophone Canadians – Anglophone Canadians • Add them all up! • Double counts anyone who speaks both. • (We’ll see how to deal with overlap later. ) Also misses anyone who speaks neither, of course!

Cases can be split into sub-cases • What’s the population of Canada? – What’s the population of BC? • • – – What’s the population of Vancouver? What’s the population of Burnaby? What’s the population of Richmond? etc. Add them all up. What’s the population of AB? What’s the population of SK? What’s the population of MB? etc. • Add them all up!

Decision Trees • When you split cases into subcases, it’s often nice to draw this as a tree. • These are informally called “decision trees”, although a proper decision tree has probabilities on branches. We’ll just ignore this. (Epp calls them “possibility trees” which is descriptive, but not standard. )

Case Splitting Example • How many different min-heaps are possible with the numbers 1, …, 7? – – – – How many have 1 at the root? How many have 2 at the root? How many have 3 at the root? How many have 4 at the root? How many have 5 at the root? How many have 6 at the root? How many have 7 at the root? • Add them all up!

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • • • And have 2 at left child? And have 3 at left child? And have 4 at left child? And have 5 at left child? And have 6 at left child? And have 7 at left child? • Add them all up! • People often draw these as trees.

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • And have 2 at left child? – And have 3 at right child? – And have 4 at right child? – And have 5 at right child? • And have 3 at left child? ? • And have 4 at left child? ? • And have 5 at left child? ?

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • And have 2 at left child? – And have 3 at right child? – And have 4 at right child? – And have 5 at right child? » 6 and 7 must be leaves of right child » Therefore 3 and 4 are leaves of left child » Therefore 4 possibilities in this case. • And have 3 at left child? ? • And have 4 at left child? ? • And have 5 at left child? ?

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • And have 2 at left child? – And have 3 at right child? – And have 4 at right child? » Right subtree leaves are 5, 6: » Right subtree leaves are 5, 7: » Right subtree leaves are 6, 7: – And have 5 at right child? 4 • And have 3 at left child? ? • And have 4 at left child? ? • And have 5 at left child? ?

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • And have 2 at left child? – And have 3 at right child? – And have 4 at right child? » Right subtree leaves are 5, 6: 4 » Right subtree leaves are 5, 7: 4 » Right subtree leaves are 6, 7: 4 – And have 5 at right child? 4 • And have 3 at left child? ? • And have 4 at left child? ? • And have 5 at left child? ?

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • And have 2 at left child? – And have 3 at right child? – And have 4 at right child? 12 – And have 5 at right child? 4 • And have 3 at left child? ? • And have 4 at left child? ? • And have 5 at left child? ?

Case Splitting: Splitting into Sub-Cases • How many different min-heaps are possible with the numbers 1, …, 7? – How many have 1 at the root? • And have 2 at left child? – And have 3 at right child? » Leftmost leaf is 4: » Leftmost leaf is 5: » Leftmost leaf is 6: » Leftmost leaf is 7: – And have 4 at right child? 12 – And have 5 at right child? 4 • And have 3 at left child? ? • And have 4 at left child? ? • And have 5 at left child? ?

Case Splitting: Splitting into Sub-Cases • How many have 1 at the root, 2 at left child, and 3 at right child: – – Leftmost leaf is 4: Leftmost leaf is 5: Leftmost leaf is 6: Leftmost leaf is 7:

Case Splitting: Splitting into Sub-Cases • How many have 1 at the root, 2 at left child, and 3 at right child: – Leftmost leaf is 4: • Next leaf is 5 • Next leaf is 6 • Next leaf is 7 – Leftmost leaf is 5: • Next leaf is 4 • Next leaf is 6 • Next leaf is 7 – Leftmost leaf is 6: – Leftmost leaf is 7:

Multiplication! E. g. : suppose there are 30 NHL teams, each with 23 players. How many players are there in total?

Multiplication! If some case split results in a bunch of identical-sized sub-cases, the total is just the number of cases times the size of each sub-case.

Multiplication! If some case split results in a bunch of identicalsized sub-cases, the total is just the number of cases times the size of each sub-case. • Note that the cases don’t have to be identical, but just have the same number of things in them.

Multiplication Principle (Product Rule) If an operation consists of t steps and: Step 1 can be performed in n 1 ways, Step 2 can be performed in n 2 ways, … Step t can be performed in nt ways, then the entire operation can be performed in n n 2…nt different ways. 1 Example: How many postal codes begin with the letter V and end with the digit 4? __ __ __

Case Splitting: Splitting into Sub-Cases • How many have 1 at the root, 2 at left child, and 3 at right child: – 4 times: • The number of cases with leftmost leaf is 4: – Next leaf is 5 – Next leaf is 6 – Next leaf is 7 4 cases with same number of elements in each one.

Case Splitting: Splitting into Sub-Cases • How many have 1 at the root, 2 at left child, and 3 at right child: – 4 times: • 3 times: – The number of cases with next leaf 5 3 cases with same number of elements in each one.

Case Splitting: Splitting into Sub-Cases • How many have 1 at the root, 2 at left child, and 3 at right child: – 4 times: • 3 times: – 2 times » 1

Permutations and Factorial The number of ways to arrange n distinct items in a row is n! – This comes straight from the product rule (which comes from case splitting) These are called permutations of the n items.

Permutations P(n, r) • What if we only want permutations of r elements out of the n objects? – E. g. , If there are 20 people here, and I have 5 different prizes to give away to people in this class, how many possible winning situations are there? – Product Rule: 20^5 if you can win repeatedly – Product Rule: 20*19*18*17*16 if you can win at most one prize.

Permutations P(n, r) Note the underline below the r. This notation is due to Knuth and is probably the most standard notation for this, but nothing is really standard.

Permutations P(n, r) You can understand this by canceling out terms. But there’s an intuitive way to understand this, too.

P(n, r)=n!/(n-r)! Intuition • How many ways to line up 20 people? • If I only give prizes to first 5, the order of remaining 15 doesn’t matter. • How many ways can I order 15 people?

P(n, r)=n!/(n-r)! Intuition • How many ways to line up 20 people? • If I only give prizes to first 5, the order of remaining 15 doesn’t matter. • How many ways can I order 15 people? • Therefore, the 20! is counting each winning possibility of the top 5 an extra 15! times. • So, the answer is 20!/15!

P(n, r)=n!/(n-r)! Intuition • How many ways to line up n people? • If I only give prizes to first r, the order of remaining (n-r) doesn’t matter. • How many ways can I order (n-r) people? • Therefore, the n! is counting each winning possibility of the top r and extra (n-r)! times. • So, the answer is n!/(n-r)!

Alan’s “Division Rule” • If the things you are trying to count are really identical-sized groupings of things from a larger set, you can divide the size of the larger set by the size of the groupings. • E. g. , if I want to know how many cars drove over a sensor strip, I can divide the number of sensor inputs by 2. Why? Steve also uses this but didn’t think to name it after himself. Drat! It’s often handy to think about this type of “overcounting”.

Division Rule and Combinations • Suppose the 5 prizes are identical, so I don’t care to distinguish who gets which prize, just who the winners are. • (This is usually phrased as choosing a committee of 5 out of the class of 20. )

Division Rule and Combinations • Suppose the 5 prizes are identical, so I don’t care to distinguish who gets which prize, just who the winners are. • I already know how many ways to get 5 winners with distinct prizes: P(n, r) • But if the prizes are the same, then any re-arranging of those 5 should only be counted once. So, I’m grouping together cases when the same 5 people get different prizes. How many cases are there?

Division Rule and Combinations • Suppose the 5 prizes are identical, so I don’t care to distinguish who gets which prize, just who the winners are. • I already know how many ways to get 5 winners with distinct prizes: P(20, 5) • But if the prizes are the same, then any re-arranging of those 5 should only be counted once. So, I’m grouping together cases when the same 5 people get different prizes. How many cases are there? 5! • Therefore, answer is P(20, 5)/5!

Division Rule and Combinations • Suppose the r prizes are identical, so I don’t care to distinguish who gets which prize, just who the winners are. • I already know how many ways to get r winners with distinct prizes: P(n, r) • But if the prizes are the same, then any re-arranging of those r should only be counted once. So, I’m grouping together cases when the same r people get different prizes. How many cases are there? r! • Therefore, answer is P(n, r)/r!

Combinations C(n, r) • These are called “combinations” – the number of ways of choosing r items out of n distinct items, where the order of those r doesn’t matter. • Pronounced “n choose r”. • AKA “binomial coefficients”

Binomial Coefficients? • If I compute (x+1)^n, what’s the coefficient of x^r • (x+1)(x+1)…(x+1) • It’s exactly C(n, r)

Dealing with Overlapping Cases • Suppose we try to compute population of the Americas by adding up the population of “North America” (defined by NAFTA as US, Canada, and Mexico) plus “Latin America” defined as countries that are predominantly Spanish- or Portuguese-speaking. • What’s wrong? How do we fix it?

Dealing with Overlapping Cases • This goes by the fancy name “inclusion-exclusion principle”, but it’s just basic sets:

Old Counting Slides These are for practice and your reference. (BTW, on my computer, many of the set symbols aren’t showing up properly. Most of them are the set “is a member of” symbol. )

Today’s Outline • • Multiplication Principle Addition Principle Inclusion/Exclusion Principle Combinations and Permutations – – – r-permutations, no repetition r-combinations, no repetition r-permutation, with repetition r-combinations, with repetition variants 61

In CS, we often encounter situations where we want to count the number of possible outcomes of an event. For example, we may wish to determine: the number of possible paths to follow in a directed network (graph), the number of possible 5 -8 character passwords, etc.

Suppose that the customers of a bank are asked to use 3 -digit PINs to protect their accounts when using the bank’s ATM machines. If the other constraints are: no 2 digits can be the same, and the only allowable digits are 1, 2, 3, & 4, how many PINs are possible? (a) Describe the problem in mathematical notation.

(b) Model the problem using a tree diagram.

Example: Use the multiplication principle to prove that the number of subsets of a set containing n elements is 2 n.

Example: Suppose a programming language requires you to define variable names (identifiers) using exactly 3 different upper case characters. How many different identifiers contain either an A or a B, but not both?

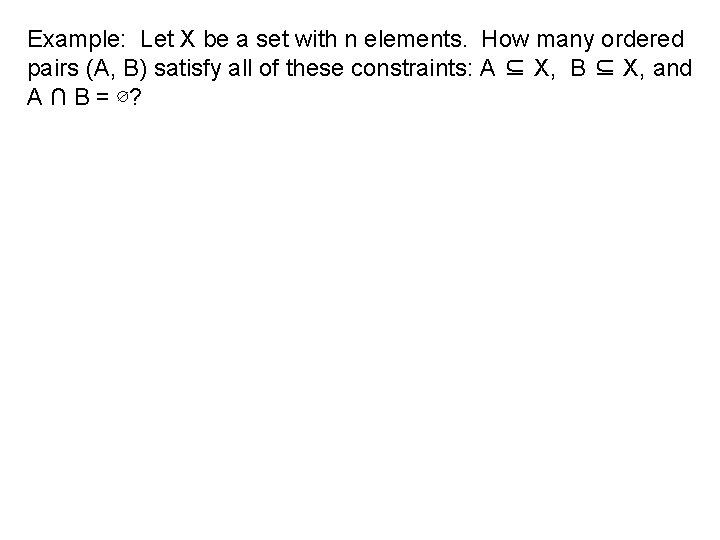
Example: Let X be a set with n elements. How many ordered pairs (A, B) satisfy all of these constraints: A ⊆ X, B ⊆ X, and A ∩ B = ∅?

Example: Suppose a user is asked to create an alphanumeric password consisting of at least 6 characters, but no more than 8 characters. How many different passwords are possible?

Back-of-the-envelope calculation. For the previous example, roughly how long would it take for a program to perform a brute -force attack to discover a user’s password, if we assume (guess? ) that a million passwords can be tested each second? Best case? Average case? Worst case? Side thought: Common passwords (when “ 128 -bit” security is no better than 10 -bit or 20 -bit security).

Example: Suppose a user is asked to create an alphanumeric password consisting of at least 6 characters, but no more than 8 characters, but this time, at least 1 of the chars. has to be a number. How many possible combinations are there this time?

Example: Suppose a user is asked to create an alphanumeric password consisting of at least 6 characters, but no more than 8 characters, but this time, at least 1 of the chars. has to be a number. Now, will the passwords be more secure or less secure?

Inclusion-Exclusion Principle If an object can be found in 2 or more sets at the same time, then we cannot use the addition principle. Why not? If A and B are sets, then the total number of elements in either A or B is given by: |A∪B| = |A|+|B| –|A∩B| Example using a Venn Diagram:

Example: How many 8 -bit strings either start with “ 1” or end with “ 00”?

Permutations & Combinations How many different outcomes are there if you choose r balls from a barrel containing n different balls?

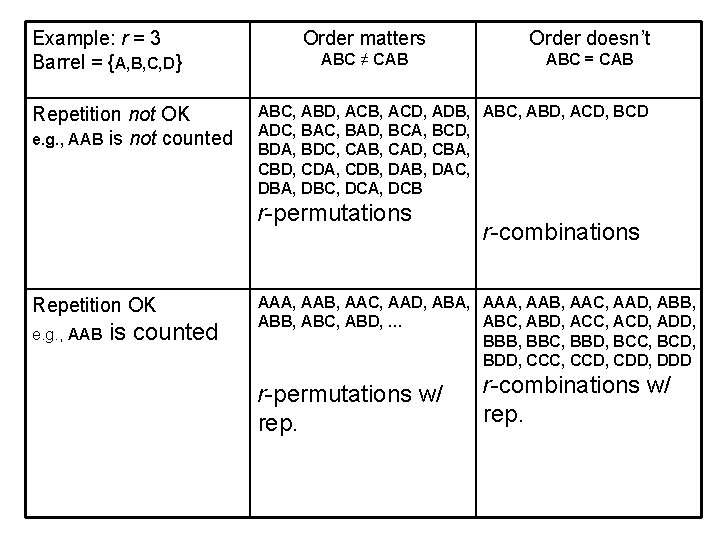
Example: r = 3 Barrel = {A, B, C, D} Repetition not OK e. g. , AAB is not counted Order matters Order doesn’t ABC ≠ CAB ABC = CAB ABC, ABD, ACB, ACD, ADB, ABC, ABD, ACD, BCD ADC, BAD, BCA, BCD, BDA, BDC, CAB, CAD, CBA, CBD, CDA, CDB, DAC, DBA, DBC, DCA, DCB r-permutations Repetition OK e. g. , AAB is counted r-combinations AAA, AAB, AAC, AAD, ABA, AAB, AAC, AAD, ABB, ABC, ABD, … ABC, ABD, ACC, ACD, ADD, BBB, BBC, BBD, BCC, BCD, BDD, CCC, CCD, CDD, DDD r-permutations w/ rep. r-combinations w/ rep.

(1) r-Permutations (Order matters, and repetition is not allowed. ) An r-permutation of n distinct elements x 1, x 2, …, xn is an ordering of an r-element subset of {x 1, x 2, …, xn}. The number of r-permutations is: P(n, r) = n(r) = Derivation:

Example 1: In how many ways can 5 electoral candidates finish in an election, assuming no ties? Example 2: In how many ways can 7 girls and 3 boys line up, if the boys must stand next to each other?

Example 3: Suppose an operating system has a queue of 3 low priority and 5 high priority processes ready to run. In how many ways could these processes be ordered for execution if 2 low priority processes are not allowed to be executed back to back?

(2) r-Combinations (Order doesn’t matter, and repetition is not allowed. ) An r-combination of n distinct elements x 1, x 2, …, xn is an relement subset of {x 1, x 2, …, xn}. The number of r-combinations is: C(n, r) = ( )= Example 4: A donut shop has 10 kinds of donuts. In how many ways can 6 distinct kinds of donuts be selected? Example 5: Show to derive a relationship between rpermutations and r-combinations.

(3) r-Permutations with Repetition (Generalized r. Permutations) Here, order matters, and repetition is allowed. Suppose we have a set of n distinct elements x 1, x 2, …, xn and we select a sequence of r elements, allowing repeats. How many different sequences are possible?

(4) r-Combinations with Repetition (Generalized r. Combinations) Here, order doesn’t matter, and repetition is allowed. Suppose we have a set of n distinct elements x 1, x 2, …, xn. The number of unordered r-element selections from this set, with repetition allowed, is:

Example 8: If a donut shop sells 3 kinds of donuts: plain, glazed, and jelly, then how many possible selections of 7 donuts are there?

Summary of Formulas Order Matters & Repetition is Order does not Matter & not Allowed Repetition is not Allowed n(r) Order Matters & Repetition is Allowed nr ( ) n r Order does not Matter & Repetition is Allowed ( ) r+n-1

Permutations of Indistinguishable Objects Multinomial Theorem: The number of different permutations of n objects where there are: n 1 indistinguishable type 1 objects n 2 indistinguishable type 2 objects … nk indistinguishable type k objects and n 1 + n 2 + … + nk = n is: Proof:

Example 9: How many strings can be made by reordering the letters PEPPER?

Theorem: The number of ways to place n distinguishable objects into r distinguishable boxes so that ni objects are placed into box i (where i = 1, 2, …, r and n 1 + n 2 + … + nr = n) is: Example 10: How many ways are there to distribute hands of 5 cards to each of 4 players from a deck of 52 cards?

Coming Up • Final Exam! Yay! 99