CPCS 204 Data Structures Algorithms Chapter 7 Trees

CPCS 204: Data Structures & Algorithms Chapter 7 Trees Instructor: Nouf Ghanimi

overview 7. 3 Binary Trees

Ordered Trees ° A tree is ordered if there is a linear ordering defined for the children of each node; ° That’s, we can identify the children of a node as being the first, second, third, and so on. ° Such an ordering is usually shown by arranging siblings left to right, according to their ordering. ° Ordered trees typically indicate the linear order among siblings by listing them in the correct order. ° A famous example of ordered trees is the family tree.

Binary Trees ° A binary tree is an ordered tree with the following properties: Every node has at most two children (called proper if 2 or 0 children). Each child node is labeled as being either a left child or a right child. A left child precedes a right child in the ordering of children of a node.

Methods of a Tree ADT 1. Accessor Methods We use positions to abstract nodes. The real power of node positions in a tree comes from the accessor methods of the tree ADT that return and accept positions, such as the following: ± root(): Return the position of the tree’s root; an error occurs if the tree is empty. ± parent(p): Return the position of the parent of p; an error occurs if p is the root. ± children(p): Return an iterable collection containing the children of node p.

Methods of a Tree ADT (Cont. ) 2. Generic methods ± size(): Return the number of nodes in the tree. ± is. Empty(): Test whether the tree has any nodes or not. ± Iterator(): Return an iterator of all the elements stored at nodes of the tree. ± positions(): Return an iterable collection of all the nodes of the tree.

Methods of a Tree ADT (Cont. ) 3. Query methods In addition to the above fundamental accessor methods, the tree ADT also supports the following Boolean query methods: is. Internal(p): Test whether node p is an internal node is. External(p): Test whether node p is an external node is. Root(p): Test whether node p is the root node These methods make programming with tree easier and more readable, ± ± ± since we can use them in the conditionals of if -statements and while -loops, rather than using a non-intuitive conditional.

Methods of a Tree ADT (Cont. ) 4. Update Method The tree ADT also supports the following update method: ± replace(p, e): Replace with e and return the element stored at node p.

Tree ADT Exceptions An interface for the tree ADT uses the following exceptions to indicate error conditions: § Invalid. Position. Exception: This error condition may be thrown by any method taking a position as an argument to indicate that the position is invalid. § Boundary. Violation. Exception: This error condition may be thrown by method parent() if it’s called on the root. § Empty. Tree. Exception: This error condition may be thrown by method root() if it’s called on an empty tree.

Binary. Tree ADT ° The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT ° Additional methods: ±position left(p) ±position right(p) ±boolean has. Left(p) ±boolean has. Right(p)

Binary Tree representation 1. Linked list 2. Array

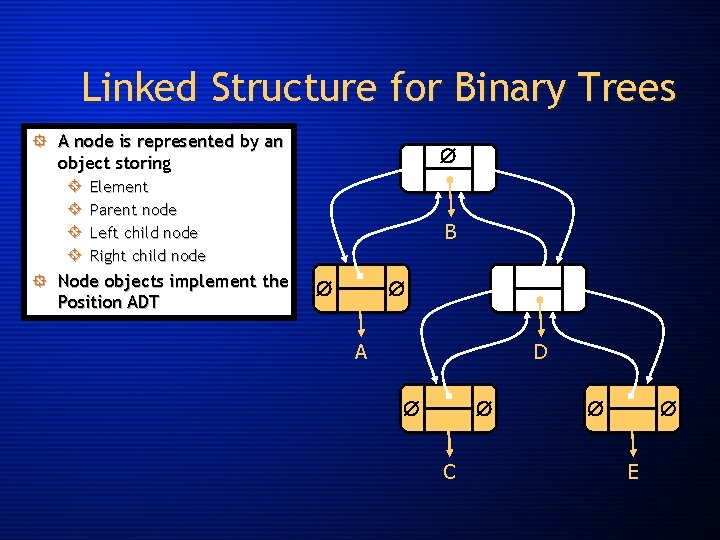
Linked Structure for Binary Trees ° A node is represented by an object storing ± ± Element Parent node Left child node Right child node ° Node objects implement the Position ADT B A D C E

Array-Based Representation of Binary Trees ° nodes are stored in an array n let rank(node) be defined as follows: n rank(root) = 1 n if node is the left child of parent(node), rank(node) = 2*rank(parent(node)) n if node is the right child of parent(node), rank(node) = 2*rank(parent(node))+1

Array Representation a 1 2 b 4 8 c d h e i tree[] 9 10 j 5 6 f 3 g 7 11 k a b c d e f g h i j k 0 5 10

Binary Tree Applications 1. 2. 3. decision processes arithmetic expressions searching

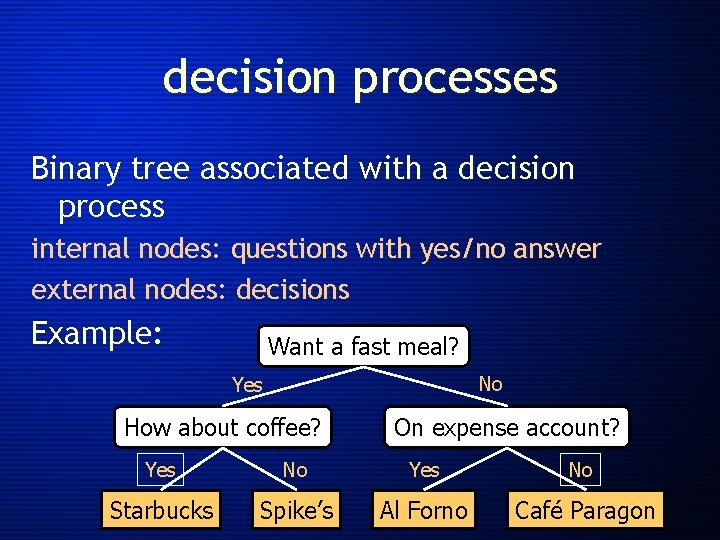
decision processes Binary tree associated with a decision process internal nodes: questions with yes/no answer external nodes: decisions Example: Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Spike’s Al Forno Café Paragon

arithmetic expressions Binary tree associated with an arithmetic expression internal nodes: operators external nodes: operands Example: (2 (a - 1) + (3 b)) + - 2 a 3 1 b

Properties of Proper Binary Trees ° Notation n number of nodes e number of external nodes i number of internal nodes h height 1 ° Properties: ±e = i + 1 ±n = 2 e - 1 ±h i ±h (n - 1)/2 ±e 2 h ±h log 2 e ±h log 2 (n + 1) - 1

Minimum Number Of Nodes °Minimum number of nodes in a binary tree whose height is h => h+1. °At least one node at each of d levels. minimum number of nodes is h+1

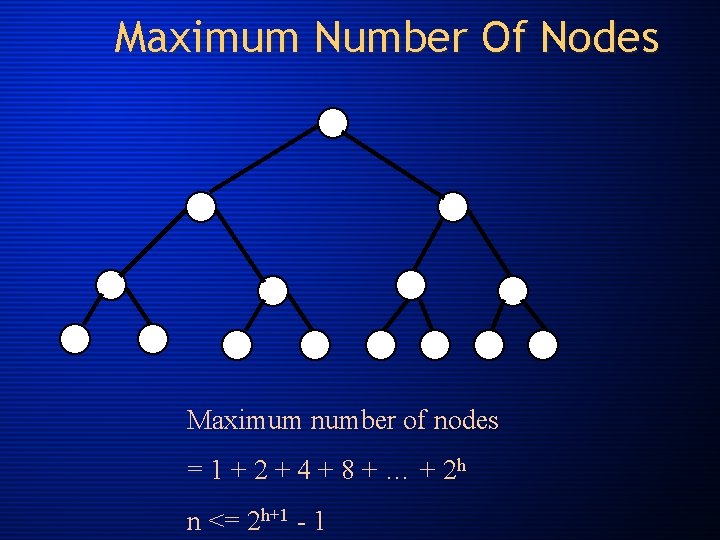
Maximum Number Of Nodes Maximum number of nodes = 1 + 2 + 4 + 8 + … + 2 h n <= 2 h+1 - 1

Full Binary Tree °A full binary tree of a given height h has 2 h+1 – 1 nodes. Height 3 full binary tree.

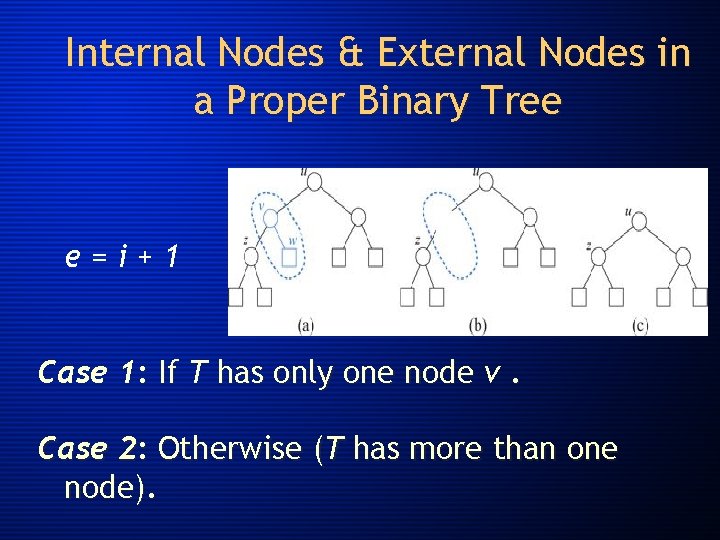
Internal Nodes & External Nodes in a Proper Binary Tree e=i+1 Case 1: If T has only one node v. Case 2: Otherwise (T has more than one node).

Binary Tree traversal 1. 2. 3. 4. Preorder Postorder Inorder Euler Tour

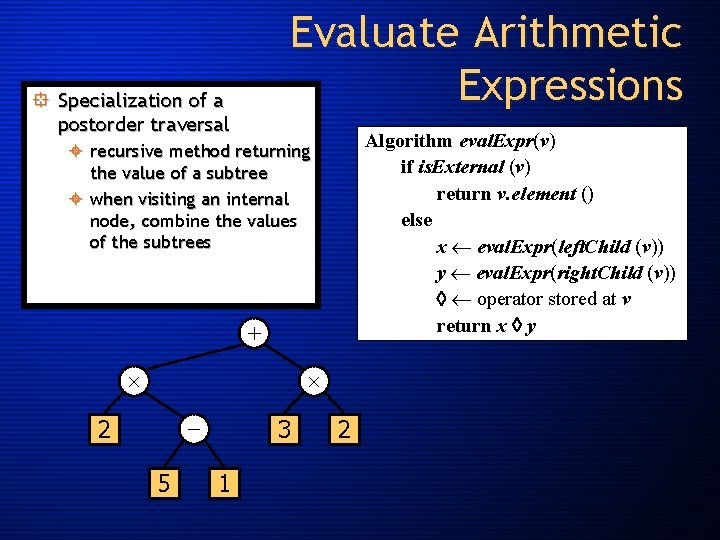
Evaluate Arithmetic Expressions ° Specialization of a postorder traversal Algorithm eval. Expr(v) if is. External (v) return v. element () else x eval. Expr(left. Child (v)) y eval. Expr(right. Child (v)) operator stored at v return x y ± recursive method returning the value of a subtree ± when visiting an internal node, combine the values of the subtrees + - 2 5 3 1 2

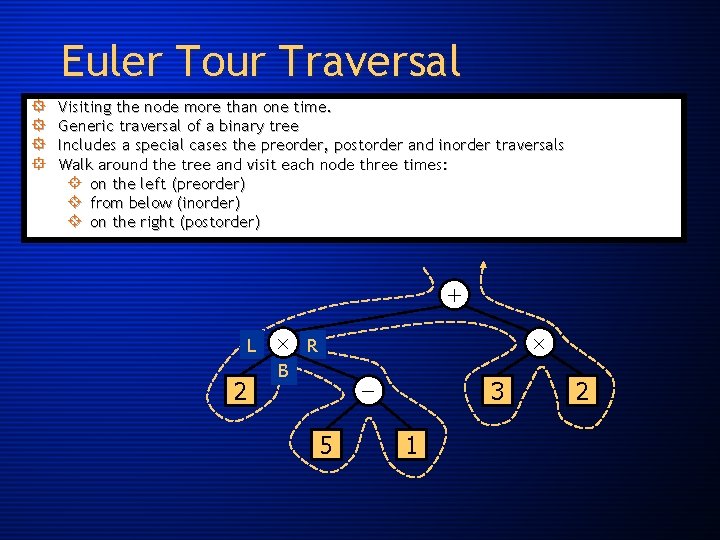
Euler Tour Traversal ° ° Visiting the node more than one time. Generic traversal of a binary tree Includes a special cases the preorder, postorder and inorder traversals Walk around the tree and visit each node three times: ± on the left (preorder) ± from below (inorder) ± on the right (postorder) + L 2 R B 5 3 1 2

Print Arithmetic Expressions Algorithm print. Expression(T, v) ((2 (a - 1)) + (3 b)) + - 2 a 3 1 b if T. is. Internal (v) then print "(" if T. has. Left (v) then print. Expression (T, T. left(v)) if T. is. Internal (v) then print the operator stored at v else print the value stored at v if T. has. Right (v) then print. Expression (T, T. right(v)) if T. is. Internal (v) then print ")"