Contest Algorithms January 2016 8 Minimal Spanning Trees

Contest Algorithms January 2016 8. Minimal Spanning Trees (MSTs) Describe a MST and the Prim and Kruskal algorithms for generating one. Contest Algorithms: 8. MSTs 1

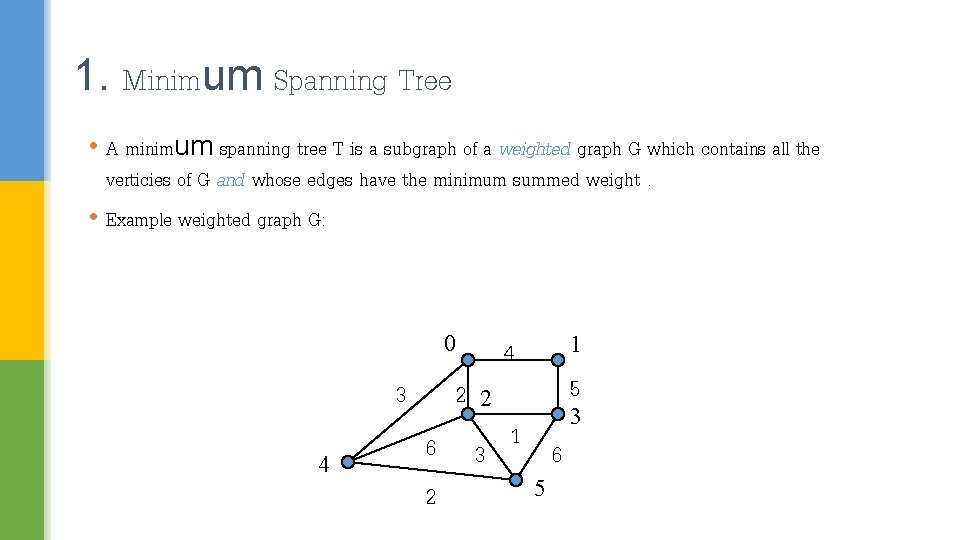
1. Minimum Spanning Tree • A minimum spanning tree T is a subgraph of a weighted graph G which contains all the verticies of G and whose edges have the minimum summed weight. • Example weighted graph G: 0 3 4 2 6 2 1 4 5 2 3 3 1 5 6

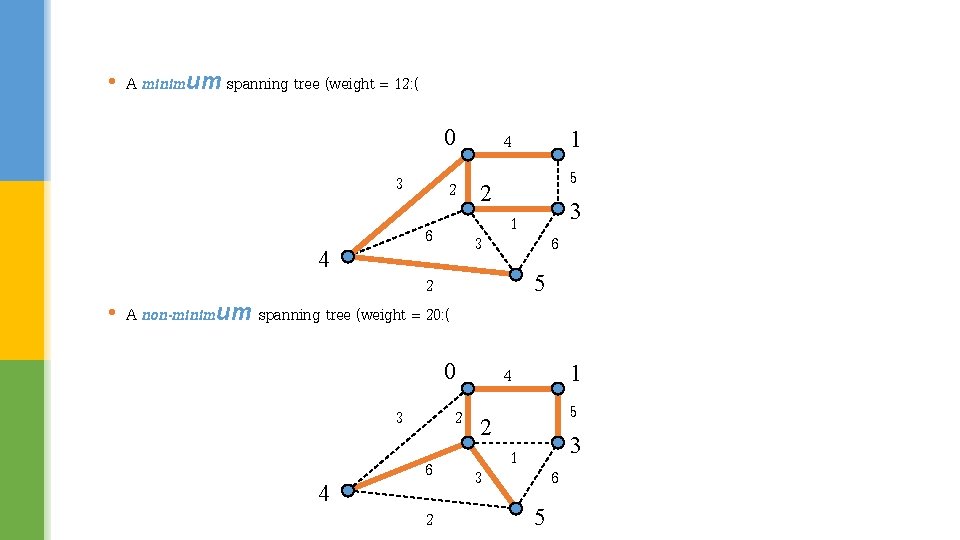
• A minimum spanning tree (weight = 12: ( 0 3 3 1 0 3 6 5 2 • A non-minimum spanning tree (weight = 20: ( 4 5 3 2 2 6 4 1 4 5 3 2 2 6 2 3 1 6 5

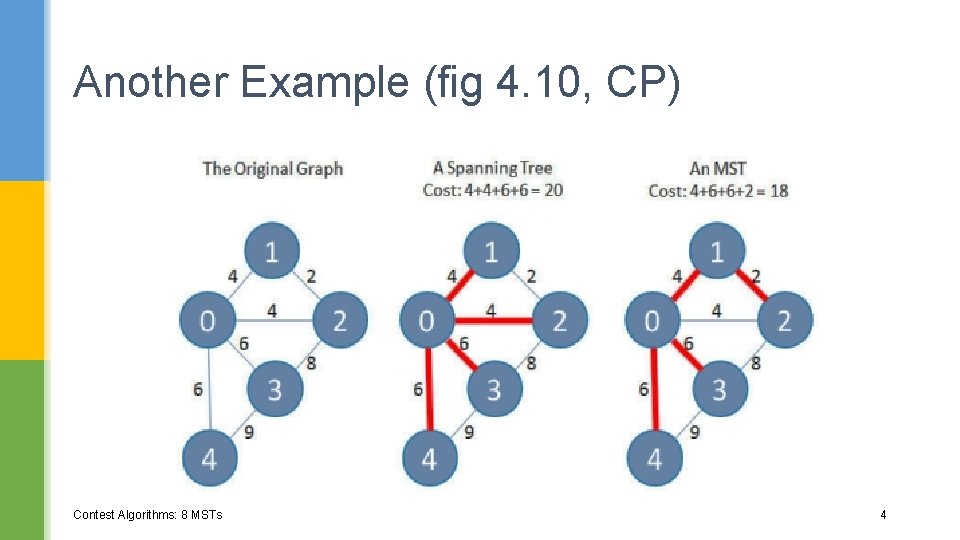
Another Example (fig 4. 10, CP) Contest Algorithms: 8 MSTs 4

2. Prim's Algorithm O(E log E) • Prim's algorithm finds a minimum spanning tree T by iteratively adding edges to T. • At each iteration, a minimum-weight edge is added that does not create a cycle in the current T. • The new edge must be connected to a vertex which is already in T. • The algorithm can stop after |V|-1 edges have been added to T. a greedy algorithm (see later)

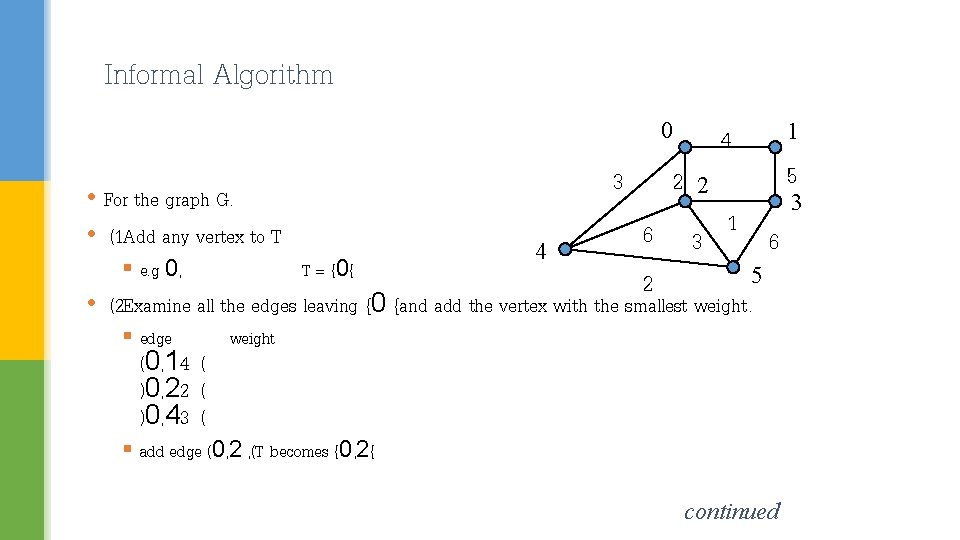
Informal Algorithm 0 • For the graph G. • (1 Add any vertex to T § e. g 0, 3 T = {0{ 4 2 6 2 1 4 5 2 3 3 1 5 6 • (2 Examine all the edges leaving {0 {and add the vertex with the smallest weight. § edge (0, 14 ( )0, 22 ( )0, 43 ( weight § add edge (0, 2 , (T becomes {0, 2{ continued

• (3 Examine all the edges leaving {0, 2 {and add the vertex with the smallest weight. § edge (0, 1)4 ( )0, 4)3 ( )2, 53 ( weight edge weight 2, 31 ( 2, 46 ( § add edge (2, 3 , (T becomes {0, 2, 3{ continued

• (4 Examine all the edges leaving {0, 2, 3 {and add the vertex with the smallest weight. § edge weight (0, 1)4 ( )0, 4)3 ( )2, 5)3 ( edge weight 3, 15 ( 2, 46 ( 3, 56 ( § add edge (0, 4 (or (2, 5 , (it does not matter § add edge (0, 4 , (T becomes {0, 2, 3, 4{ continued

• (5 Examine all the edges leaving {0, 2, 3, 4 {and add the vertex with the smallest weight. § edge (0, 1)4 ( )2, 5)3 ( )4, 52 ( weight edge weight 3, 15 ( 3, 56 ( § add edge (4, 5 , (T becomes {0, 2, 3, 4, 5{ continued

• (6 Examine all the edges leaving {0, 2, 3, 4, 5 {and add the vertex with the smallest weight. § edge (0, 1)4 ( weight edge weight 3, 15 ( § add edge (0, 1 , (T becomes {0, 1, 2, 3, 4, 5{ • All the verticies of G are now in T, so we stop. continued

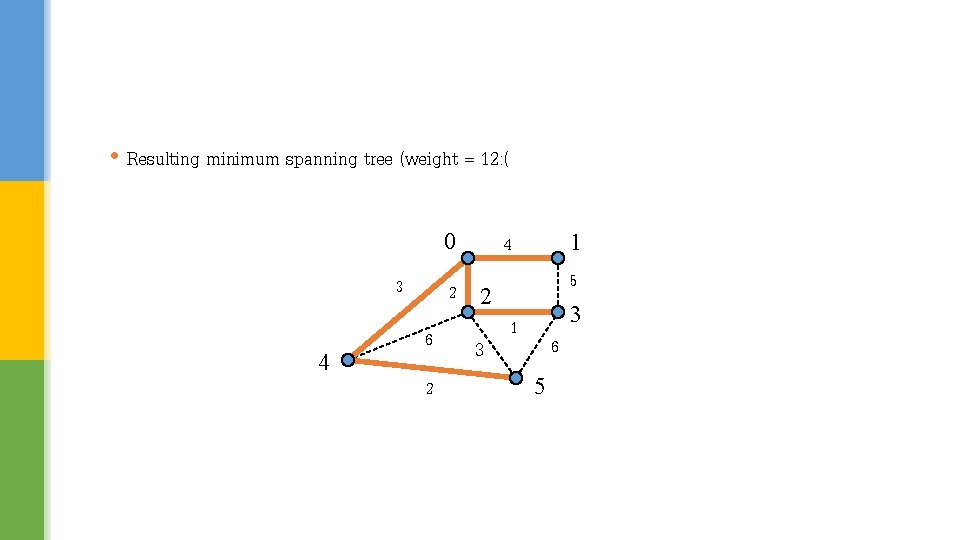
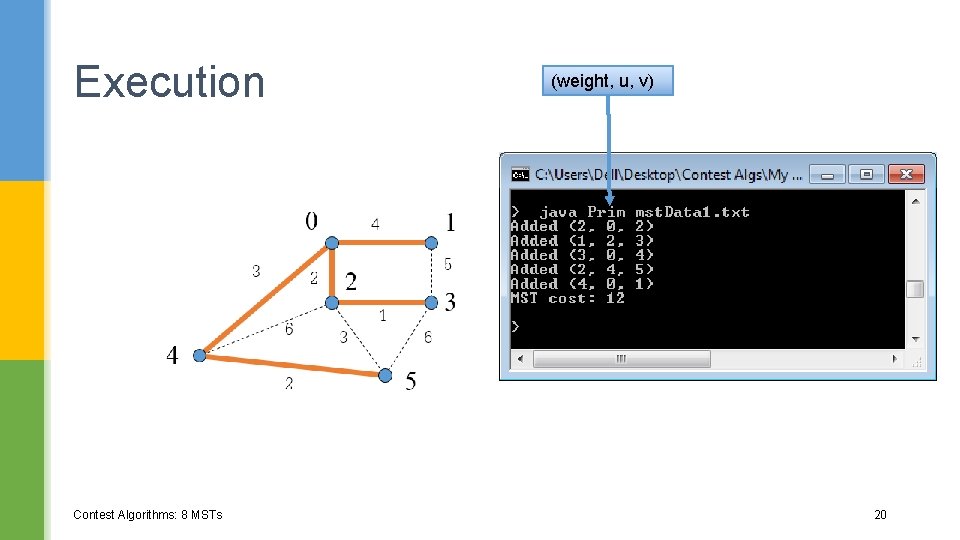
• Resulting minimum spanning tree (weight = 12: ( 0 3 4 1 4 5 3 2 2 6 2 3 1 6 5

Input Data Format § no. of vertices, no. of edges § triple of numbers: one triple is an edge (u v) and weight w which must be recorded twice in the list: once for u --> v, once for v --> u e. g. 57 014 024 036 046 122 238 349 Contest Algorithms: 8 MSTs 12

Main Data Structures for Prim's § An adjacency list for a undirected, unweighted graph. § A priority queue of (weight, u, v) triples in increasing weight order. § A boolean array to make if a vertex has been visited. private static Array. List<IPair>> adj. List; private static Priority. Queue<ITriple> pq; private static boolean[] visited; Contest Algorithms: 8 MSTs 13

Code see Prim. java public static void main(String[] args) throws Exception { if (args. length != 1) { System. out. println("Usage: java Prim <data-file>"); return; } Scanner sc = new Scanner(new File(args[0])); int num. Vs = sc. next. Int(); int num. Es = sc. next. Int(); adj. List = new Array. List<>(); for (int i = 0; i < num. Vs; i++) { Array. List<IPair> neighbors = new Array. List<IPair>(); adj. List. add(neighbors); } for (int i = 0; i < num. Es; i++) { int u = sc. next. Int(); int v = sc. next. Int(); int weight = sc. next. Int(); adj. List. get(u). add( new IPair(v, weight)); // u --> v adj. List. get(v). add( new IPair(u, weight)); // v --> u } : Contest Algorithms: 8 MSTs 14

pq = new Priority. Queue<ITriple>(); // pri-queue of (weight, u, v) triples visited = new boolean[num. Vs]; // will contain all falses by default queue. Neighbors(0); // queue neighbors of vertex 0 int mst. Cost = 0; while (!pq. is. Empty()) { // repeat until all vertices have been visited ITriple s. Edge = pq. peek(); // (weight, u, v) pq. poll(); int v = s. Edge. get. Z(); if (!visited[v]) { // this vertex not in mst. Cost += s. Edge. get. X(); System. out. println("Added " + s. Edge); queue. Neighbors(v); // take v, queue all edges incident to v } } System. out. println("MST cost: " + mst. Cost); } // end of main() Contest Algorithms: 8 MSTs 15

private static void queue. Neighbors(int v) /* queue all edges incident to v in the priority queue, and marked v as visited */ { visited[v] = true; Array. List<IPair> neighbors = adj. List. get(v); // list of (vertex, weight) pairs for (IPair p : neighbors) { if (!visited[p. get. X()]) pq. offer( new ITriple(p. get. Y(), v, p. get. X())); // (weight, v, neighbour) triple } } // end of queue. Neighbors() Contest Algorithms: 8 MSTs 16

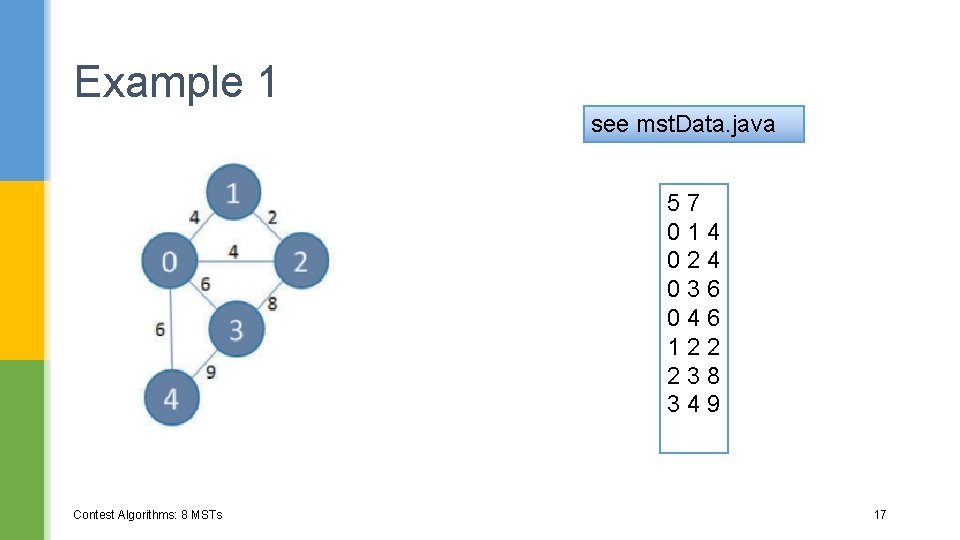
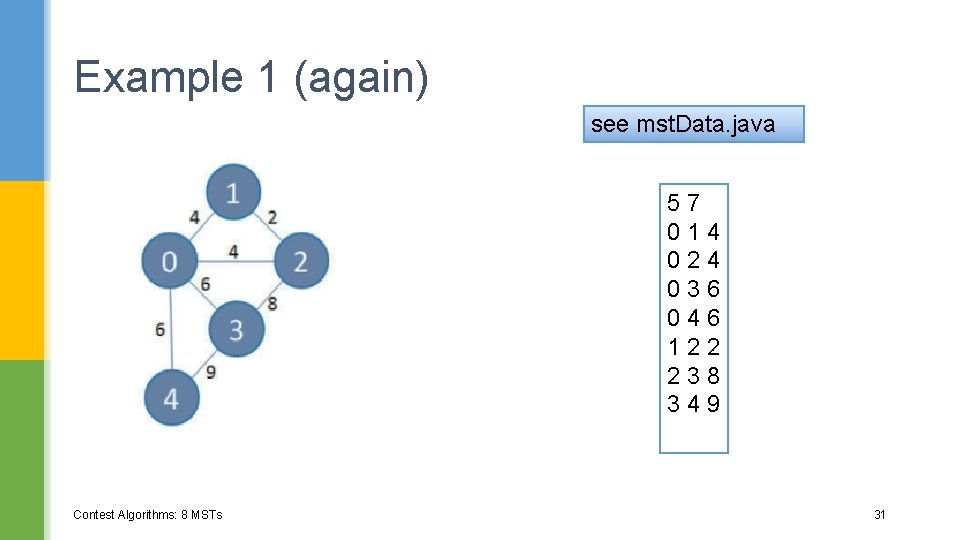
Example 1 see mst. Data. java 57 014 024 036 046 122 238 349 Contest Algorithms: 8 MSTs 17

Execution Contest Algorithms: 8 MSTs (weight, u, v) 18

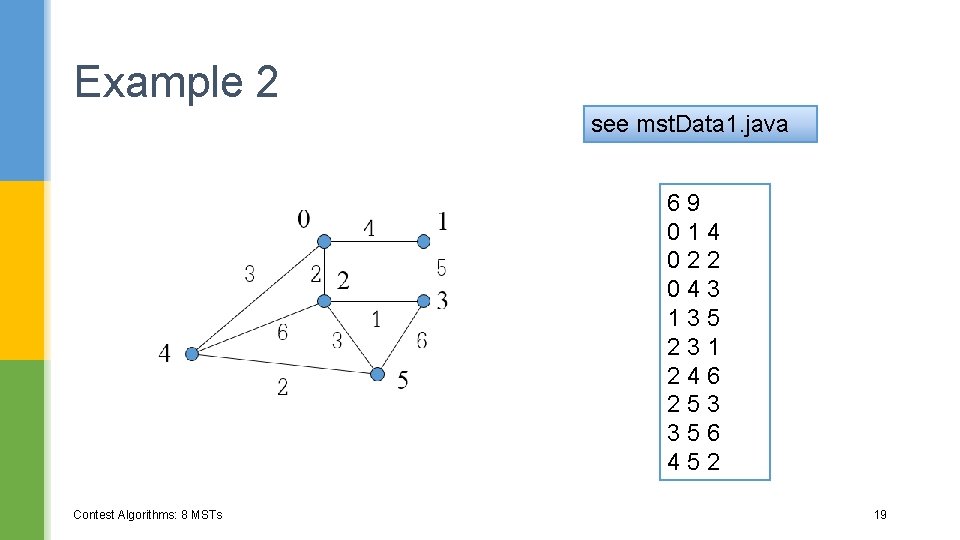
Example 2 see mst. Data 1. java 69 014 022 043 135 231 246 253 356 452 Contest Algorithms: 8 MSTs 19

Execution Contest Algorithms: 8 MSTs (weight, u, v) 20

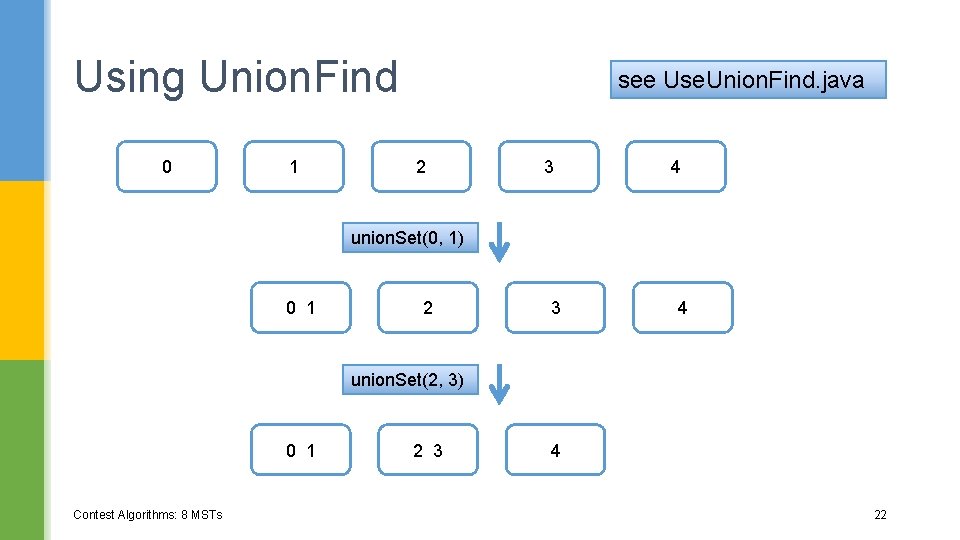
3. Union-find see Union. Find. java § A disjoint-set data structure keeps track of a set of elements split into disjoint (non-overlapping) subsets. § Union-find consists of two main operations: § find. Set(): report which subset a particular element is in § union. Set(): join two subsets into a single subset § others: make. Sets(), is. Connected(), etc.

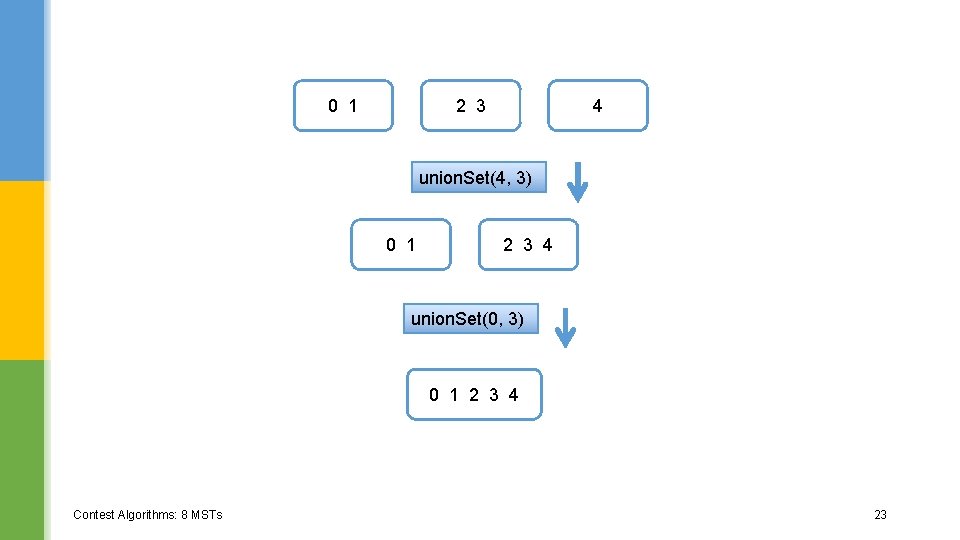
Using Union. Find 0 1 see Use. Union. Find. java 2 3 4 union. Set(0, 1) 0 1 2 3 4 union. Set(2, 3) 0 1 Contest Algorithms: 8 MSTs 2 3 4 22

0 1 4 2 3 union. Set(4, 3) 0 1 2 3 4 union. Set(0, 3) 0 1 2 3 4 Contest Algorithms: 8 MSTs 23

4. Kruskal's Algorithm O(E log E), same as Prim's § Krukal's algorithm finds a minimum spanning tree T by iteratively adding edges to T. § At each iteration, a minimum-weight edge is added that does not create a cycle in the current T. § The new edge can come from anywhere in G. § The algorithm can stop after |V|-1 edges have been added to T. a greedy algorithm (see later)

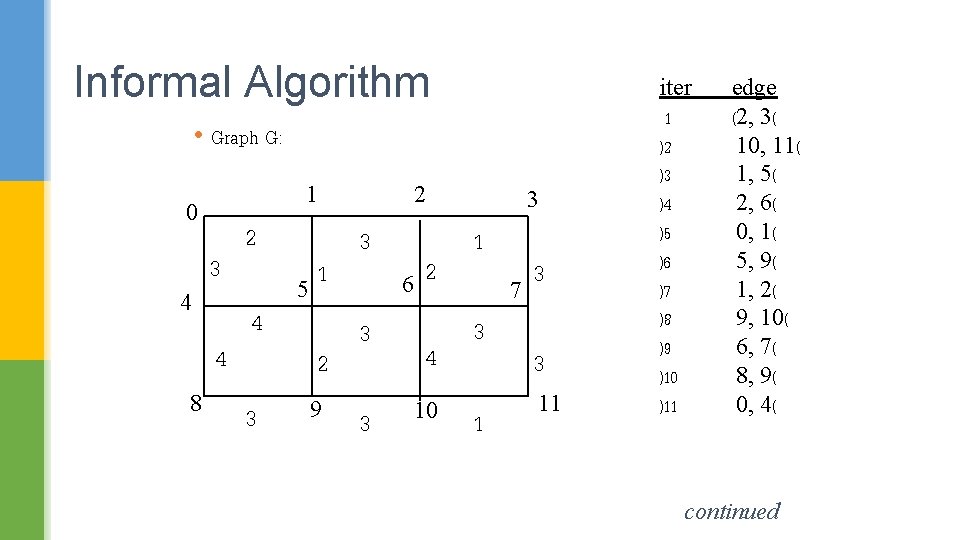
Informal Algorithm • Graph G: 1 0 4 3 4 8 2 4 3 5 2 1 2 9 3 2 6 3 3 3 4 10 1 7 3 1 3 3 11 iter 1 )2 )3 )4 )5 )6 )7 )8 )9 )10 )11 edge (2, 3( 10, 11( 1, 5( 2, 6( 0, 1( 5, 9( 1, 2( 9, 10( 6, 7( 8, 9( 0, 4( continued

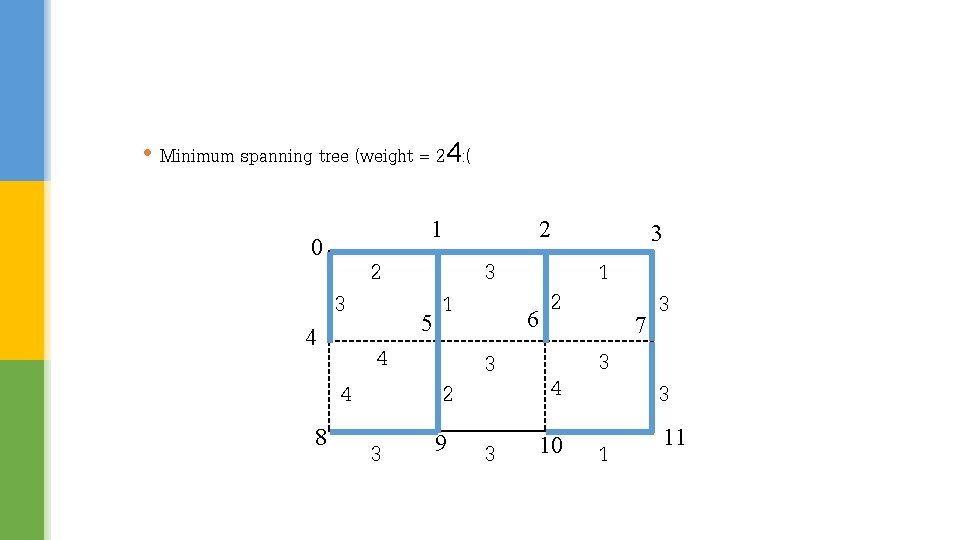
• Minimum spanning tree (weight = 24: ( 1 0 4 3 4 8 2 4 3 5 2 1 2 9 3 2 6 3 3 3 4 10 1 7 3 1 3 3 11

Input Data Format Same as for Prim. java § no. of vertices, no. of edges § triple of numbers: one triple is an edge (u v) and weight w which must be recorded twice in the list: once for u --> v, once for v --> u e. g. 57 014 024 036 046 122 238 349 Contest Algorithms: 8 MSTs 27

Main Data Structures for Kruskal's § An adjacency list for a undirected, unweighted graph. § same as for Prim's algorithm § An edges list containing (weight, u, v) triples. § Use Union. Find to containing the growing sub-trees that eventually join together to create the MST. Array. List<IPair>> adj. List; Array. List<ITriple> edges. List; Union. Find uf = new Union. Find(num. Vs); Contest Algorithms: 8 MSTs 28

Code see Kruskal. java Contest Algorithms: 8 MSTs public static void main(String[] args) throws Exception { if (args. length != 1) { System. out. println("Usage: java Kruskal <data-file>"); return; } Scanner sc = new Scanner(new File(args[0])); int num. Vs = sc. next. Int(); int num. Es = sc. next. Int(); Array. List<IPair>> adj. List = new Array. List<>(); for (int i = 0; i < num. Vs; i++) { Array. List<IPair> neighbors = new Array. List<IPair>(); adj. List. add(neighbors); } Array. List<ITriple> edges. List = new Array. List<ITriple>(); for (int i = 0; i < num. Es; i++) { int u = sc. next. Int(); int v = sc. next. Int(); int weight = sc. next. Int(); edges. List. add( new ITriple(weight, u, v)); adj. List. get(u). add( new IPair(v, weight)); // u --> v adj. List. get(v). add( new IPair(u, weight)); // v --> u } Collections. sort(edges. List); // sort into increasing weight : 29

int mst. Cost = 0; Union. Find uf = new Union. Find(num. Vs); // all verts are in their own disjoint sets initially for (int i = 0; i < num. Es; i++) { ITriple s. Edge = edges. List. get(i); // smallest edge (weight, u, v) if (!uf. in. Same. Set(s. Edge. get. Y(), s. Edge. get. Z())) { // if u and v in separate sets System. out. println("Added " + s. Edge); mst. Cost += s. Edge. get. X(); // add weight uf. union. Set(s. Edge. get. Y(), s. Edge. get. Z()); // join u and v sets } } // the number of sets must eventually be 1 for a valid MST System. out. println("MST cost: " + mst. Cost); } // end of main() Contest Algorithms: 8 MSTs 30

Example 1 (again) see mst. Data. java 57 014 024 036 046 122 238 349 Contest Algorithms: 8 MSTs 31

Execution (weight, u, v) The same result, but the edge choice order is different. Contest Algorithms: 8 MSTs 32

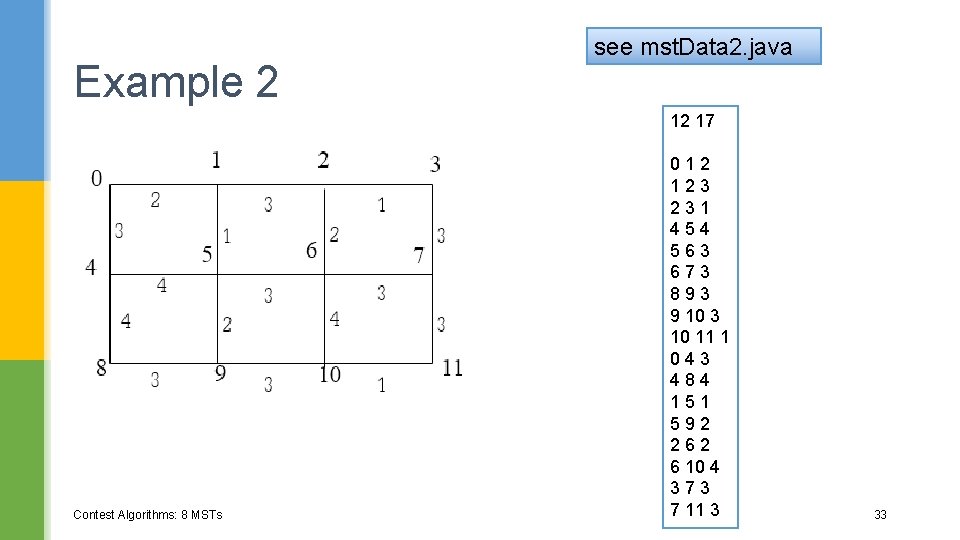
Example 2 see mst. Data 2. java 12 17 Contest Algorithms: 8 MSTs 012 123 231 454 563 673 893 9 10 3 10 11 1 043 484 151 592 262 6 10 4 373 7 11 3 33

Execution Contest Algorithms: 8 MSTs (weight, u, v) 34

5. Differences between Prim and Kruskal • Prim's algorithm chooses an edge that must be connected to a vertex in the minimum spanning tree T. • Kruskal's algorithm chooses an edge from G that may or may not be connected to a vertex in T. • They have the same big-oh running times, but Kruskal's algorithm can be faster for sparse graphs.

§ My version of Prim's algorithm uses a priority queue, which is implemented in Java using a binary heap. § If a Fibonacci heap is used instead, Prim's can be made faster than Kruskal's. § Prims only gives a MST if the graph is connected. § Kruskal will can handle a disconnected graph, outputting a Minimum Spanning forest Contest Algorithms: 8 MSTs 36