Chapter 5 Introduction to Factorial Designs 1 5






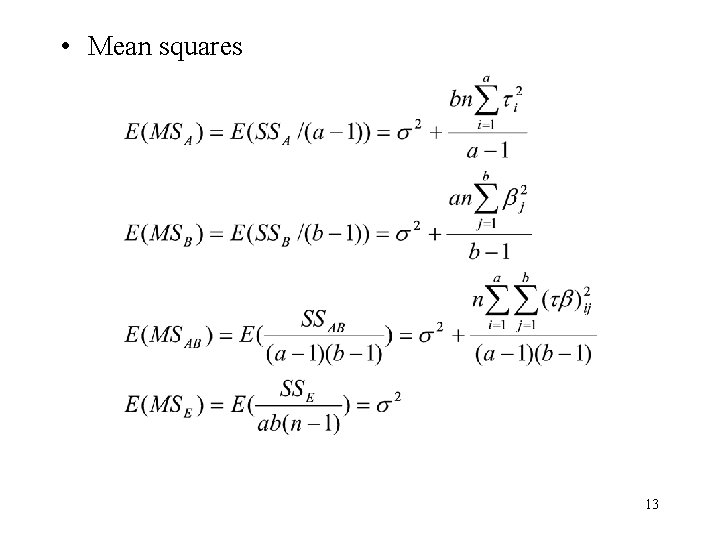










- Slides: 28

Chapter 5 Introduction to Factorial Designs 1

5. 1 Basic Definitions and Principles • • Study the effects of two or more factors. Factorial designs Crossed: factors are arranged in a factorial design Main effect: the change in response produced by a change in the level of the factor 2

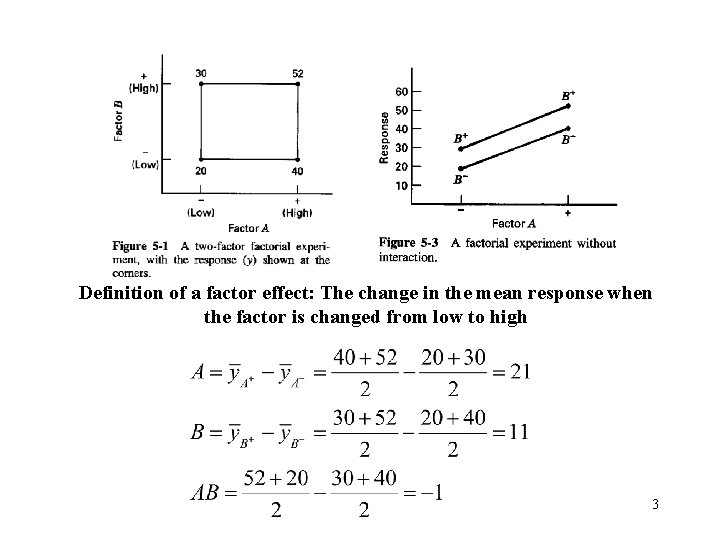
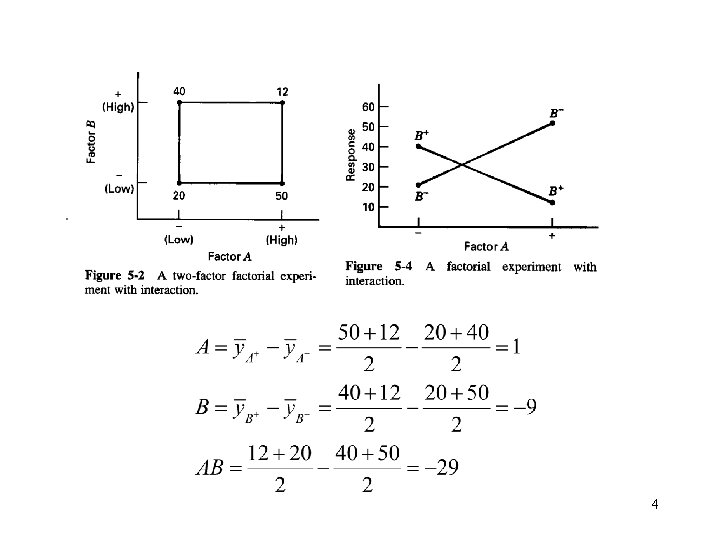
Definition of a factor effect: The change in the mean response when the factor is changed from low to high 3

4

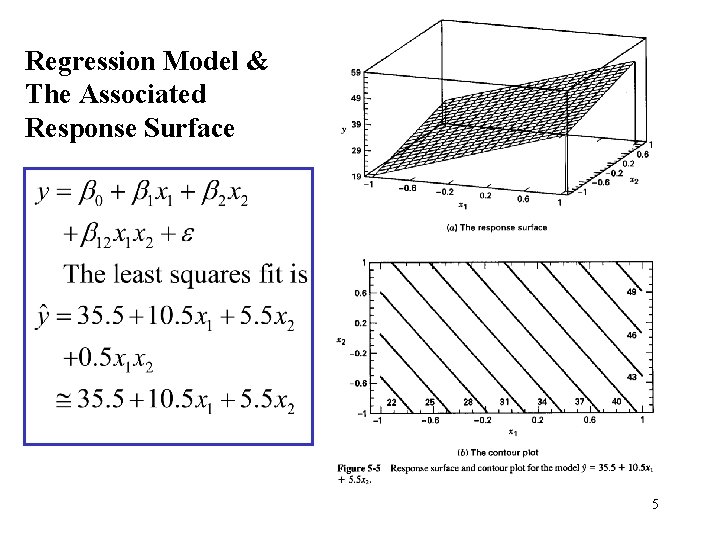
Regression Model & The Associated Response Surface 5

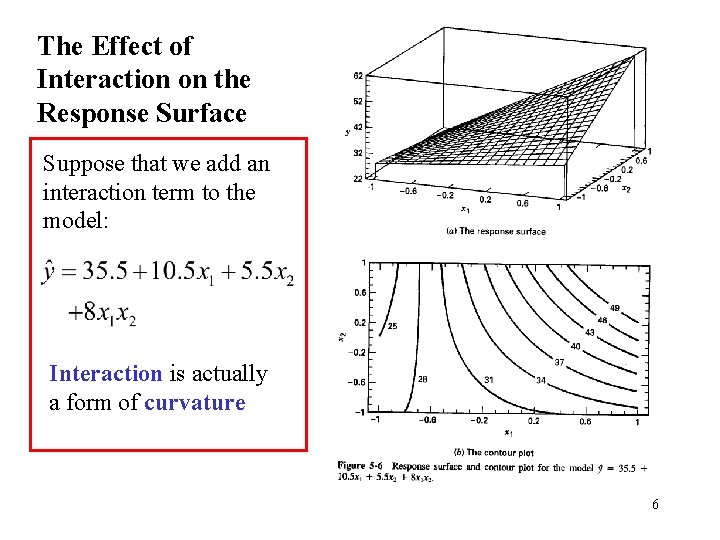
The Effect of Interaction on the Response Surface Suppose that we add an interaction term to the model: Interaction is actually a form of curvature 6

• When an interaction is large, the corresponding main effects have little practical meaning. • A significant interaction will often mask the significance of main effects. 7

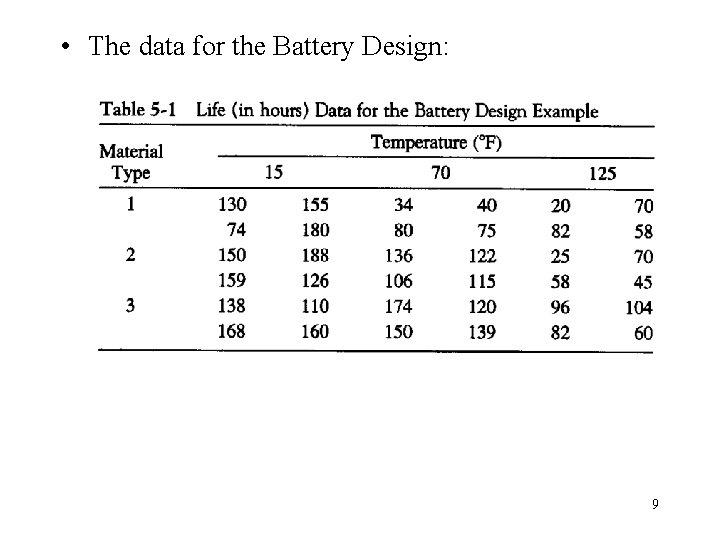
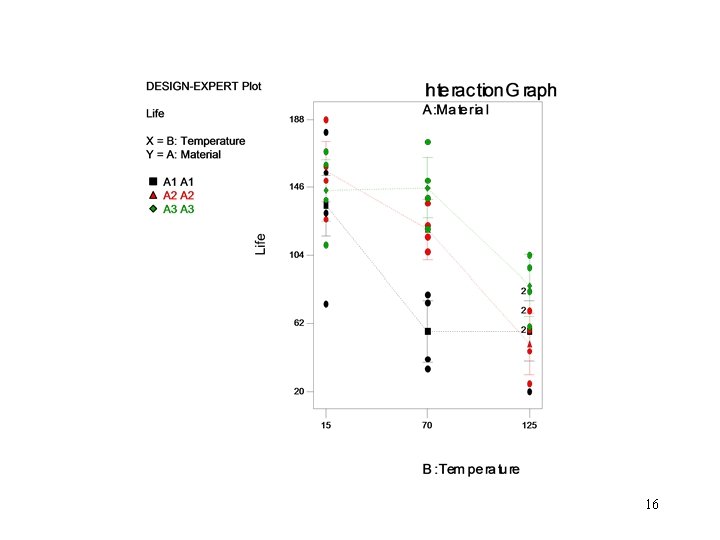
5. 3 The Two-Factorial Design 5. 3. 1 An Example • a levels for factor A, b levels for factor B and n replicates • Design a battery: the plate materials (3 levels) v. s. temperatures (3 levels), and n = 4 • Two questions: – What effects do material type and temperature have on the life of the battery? – Is there a choice of material that would give uniformly long life regardless of temperature? 8

• The data for the Battery Design: 9

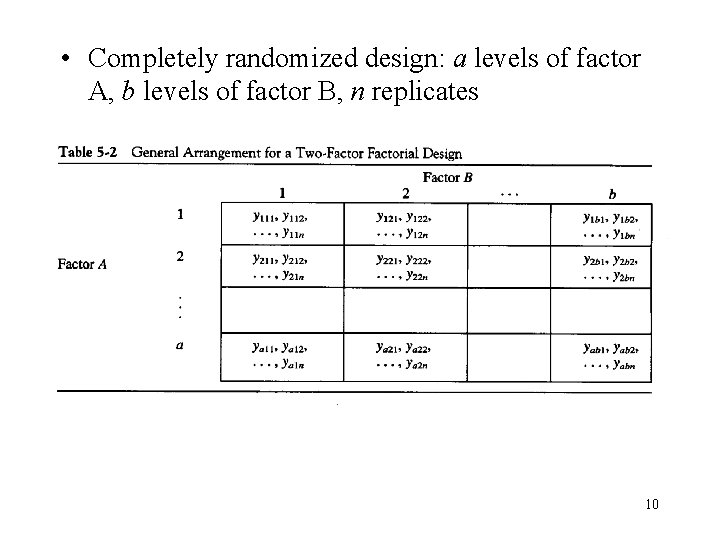
• Completely randomized design: a levels of factor A, b levels of factor B, n replicates 10

• Statistical (effects) model: • Testing hypotheses: 11

• 5. 3. 2 Statistical Analysis of the Fixed Effects Model 12
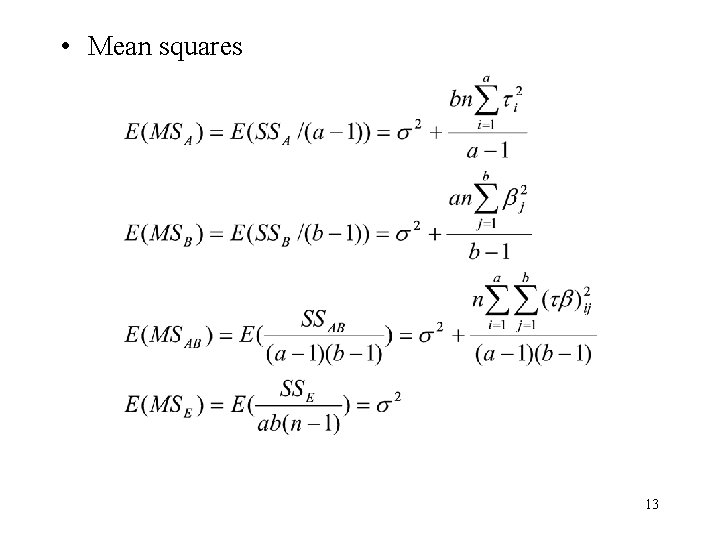
• Mean squares 13

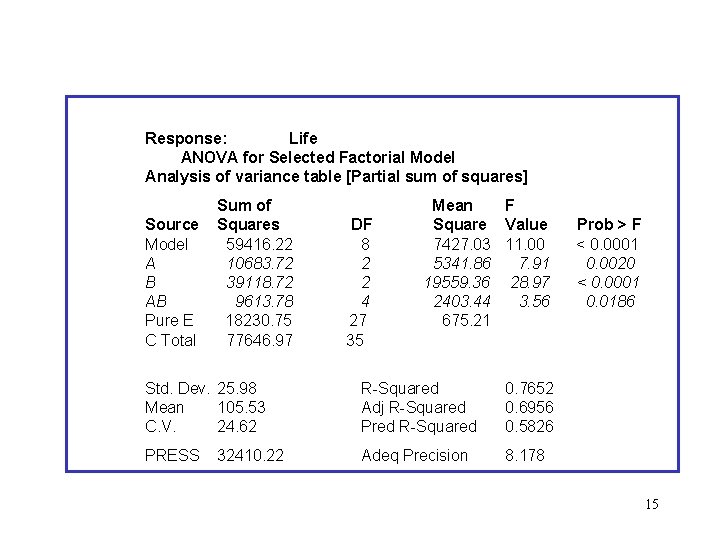
• The ANOVA table: • See Page 180 • Example 5. 1 14

Response: Life ANOVA for Selected Factorial Model Analysis of variance table [Partial sum of squares] Source Model A B AB Pure E C Total Sum of Squares 59416. 22 10683. 72 39118. 72 9613. 78 18230. 75 77646. 97 DF 8 2 2 4 27 35 Mean F Square Value 7427. 03 11. 00 5341. 86 7. 91 19559. 36 28. 97 2403. 44 3. 56 675. 21 Std. Dev. 25. 98 Mean 105. 53 C. V. 24. 62 R-Squared Adj R-Squared Pred R-Squared 0. 7652 0. 6956 0. 5826 PRESS Adeq Precision 8. 178 32410. 22 Prob > F < 0. 0001 0. 0020 < 0. 0001 0. 0186 15

16

• Multiple Comparisons: – Use the methods in Chapter 3. – Since the interaction is significant, fix the factor B at a specific level and apply Turkey’s test to the means of factor A at this level. – See Pages 182, 183 – Compare all ab cells means to determine which one differ significantly 17

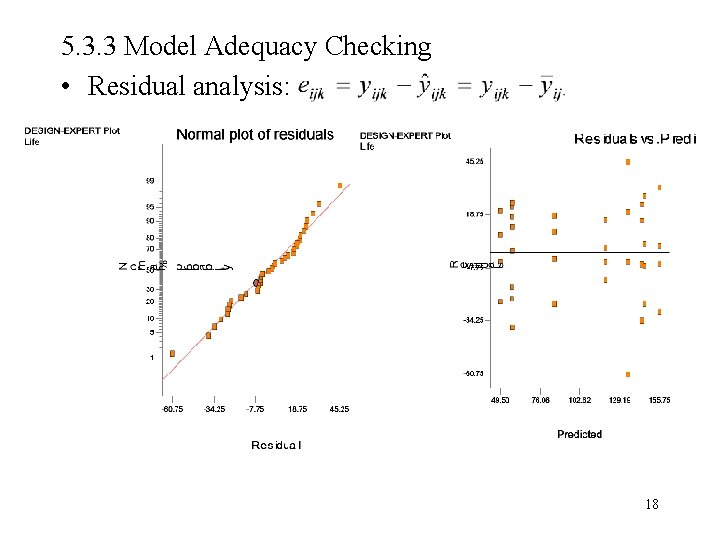
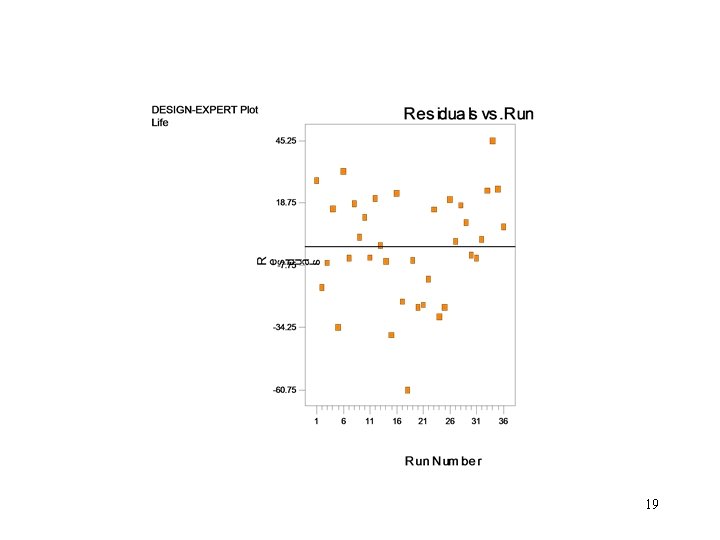
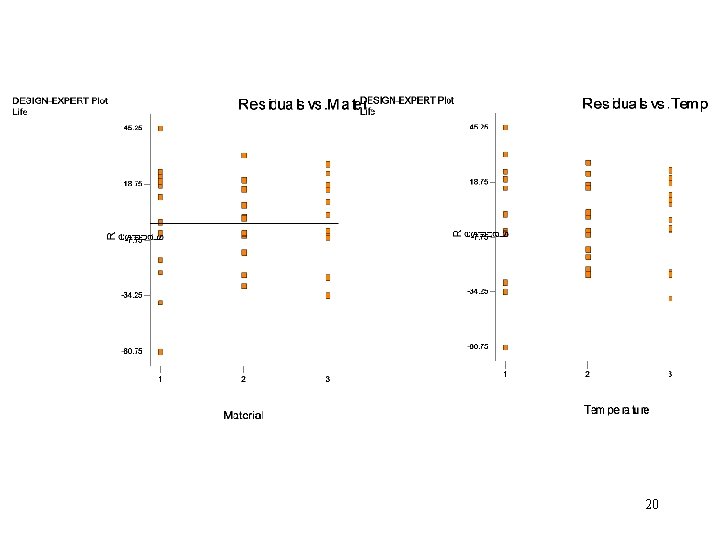
5. 3. 3 Model Adequacy Checking • Residual analysis: 18

19

20

5. 3. 4 Estimating the Model Parameters • The model is • The normal equations: • Constraints: 21

• Estimations: • The fitted value: • Choice of sample size: Use OC curves to choose the proper sample size. 22

• Consider a two-factor model without interaction: – Table 5. 8 – The fitted values: – Figure 5. 15 • One observation per cell: – The error variance is not estimable because the two-factor interaction and the error can not be separated. – Assume no interaction. (Table 5. 9) – Tukey (1949): assume ( )ij = r i j (Page 192) – Example 5. 2 23

5. 4 The General Factorial Design • More than two factors: a levels of factor A, b levels of factor B, c levels of factor C, …, and n replicates. • Total abc … n observations. • For a fixed effects model, test statistics for each main effect and interaction may be constructed by dividing the corresponding mean square for effect or interaction by the mean square error. 24

• Degree of freedom: – Main effect: # of levels – 1 – Interaction: the product of the # of degrees of freedom associated with the individual components of the interaction. • The three factor analysis of variance model: – – The ANOVA table (see Table 5. 12) – Computing formulas for the sums of squares (see Page 196) – Example 5. 3 25

5. 5 Fitting Response Curves and Surfaces • An equation relates the response (y) to the factor (x). • Useful for interpolation. • Linear regression methods • Example 5. 4 – Study how temperatures affects the battery life – Hierarchy principle • Example 5. 5 26

5. 6 Blocking in a Factorial Design • A nuisance factor: blocking • A single replicate of a complete factorial experiment is run within each block. • Model: – No interaction between blocks and treatments • ANOVA table (Table 5. 18) • Example 5. 6 27

• Two randomization restrictions: Latin square design • An example in Page 209 • Model: • Table 5. 22 28