Experiment Basics Designs Psych 231 Research Methods in

Experiment Basics: Designs Psych 231: Research Methods in Psychology

Exam 2 a week from today n First draft of Class Experiment APA paper due in Labs this week n Announcements

n n So far we’ve covered a lot of the about details experiments generally Now let’s consider some specific experimental designs. n n Some bad (but common) designs Some good designs • • 1 Factor, two levels 1 Factor, multi-levels Factorial (more than 1 factor) Between & within factors Experimental designs
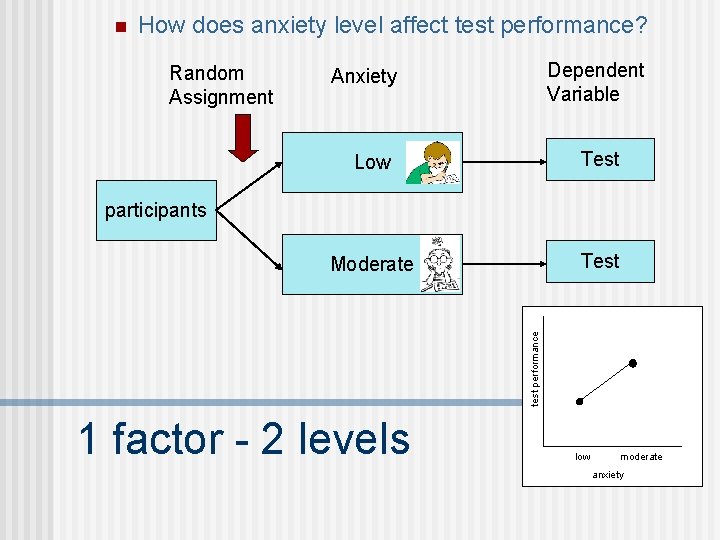
n How does anxiety level affect test performance? Random Assignment Dependent Variable Anxiety Low Test Moderate Test test performance participants 1 factor - 2 levels low moderate anxiety
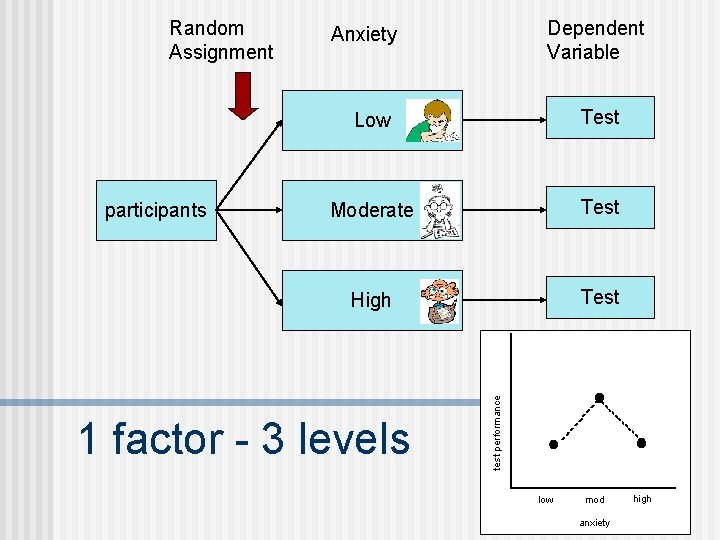
participants Dependent Variable Anxiety Low Test Moderate Test High Test 1 factor - 3 levels test performance Random Assignment low mod anxiety high

n Two or more factors n Some vocabulary • Factors - independent variables • Levels - the levels of your independent variables • 2 x 4 design means two independent variables, one with 2 levels and one with 4 levels • “Conditions” or “groups” is calculated by multiplying the levels, so a 2 x 4 design has 8 different conditions A 1 B 2 B 3 B 4 A 2 Factorial experiments

Two or more factors n n Main effects - the effects of your independent variables ignoring (collapsed across) the other independent variables Interaction effects - how your independent variables affect each other • Example: 2 x 2 design, factors A and B B 1 • Interaction: • At A 1, B 1 is bigger than B 2 • At A 2, B 1 and B 2 don’t differ Dependent Variable n B 2 A 1 A Everyday interaction = “it depends on …” Factorial experiments
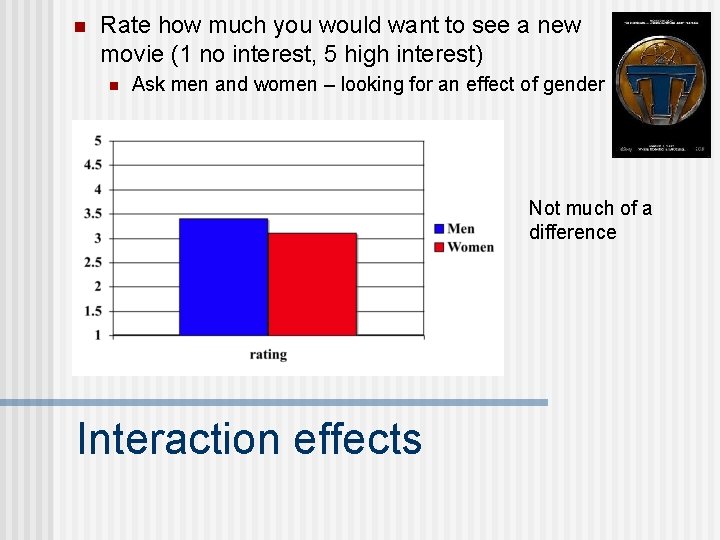
n Rate how much you would want to see a new movie (1 no interest, 5 high interest) n Ask men and women – looking for an effect of gender Not much of a difference Interaction effects
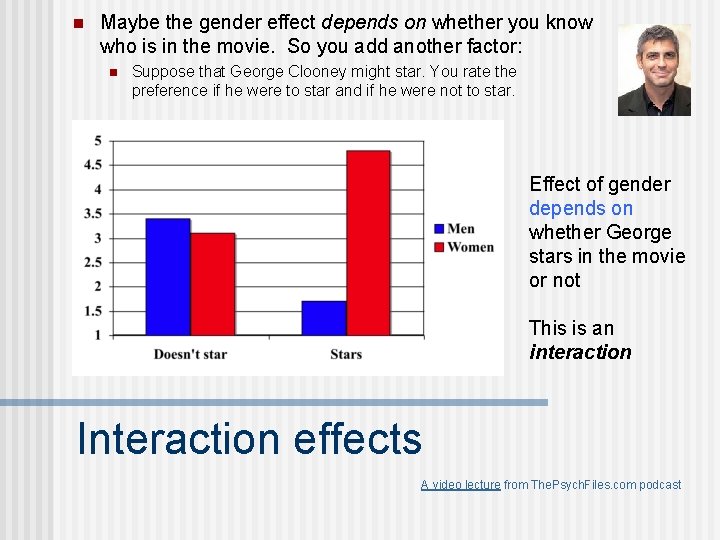
n Maybe the gender effect depends on whether you know who is in the movie. So you add another factor: n Suppose that George Clooney might star. You rate the preference if he were to star and if he were not to star. Effect of gender depends on whether George stars in the movie or not This is an interaction Interaction effects A video lecture from The. Psych. Files. com podcast

n The complexity & number of outcomes increases: • A = main effect of factor A • B = main effect of factor B • AB = interaction of A and B • With 2 factors there are 8 basic possible patterns of results: 1) No effects at all 2) A only 3) B only 4) AB only 5) A & B 6) A & AB 7) B & AB 8) A & B & AB Results of a 2 x 2 factorial design
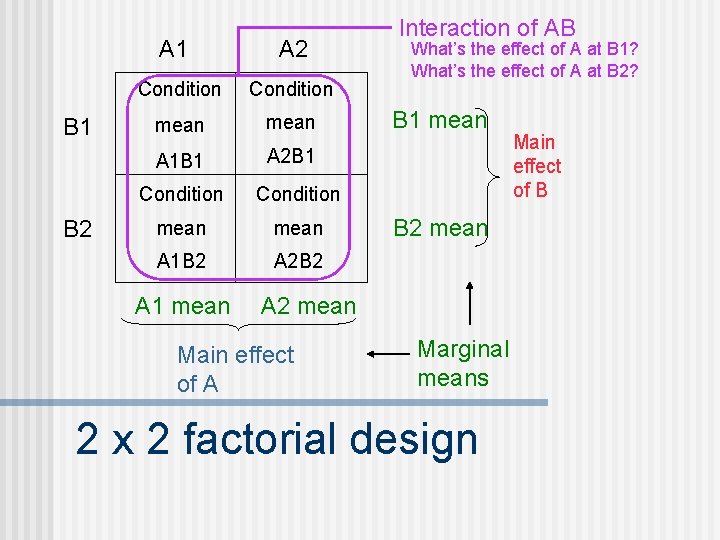
A 1 B 2 A 2 Condition mean A 1 B 1 A 2 B 1 Condition mean A 1 B 2 A 2 B 2 A 1 mean Interaction of AB What’s the effect of A at B 1? What’s the effect of A at B 2? B 1 mean B 2 mean A 2 mean Main effect of A Marginal means 2 x 2 factorial design Main effect of B
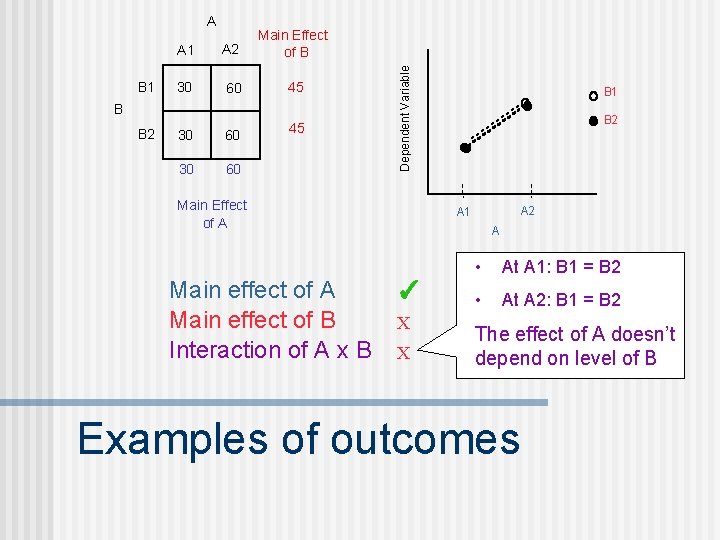
A 1 A 2 Main Effect of B B 1 30 60 45 B 2 30 60 B 45 Dependent Variable A Main Effect of A Main effect of B Interaction of A x B B 1 B 2 A 1 A ✓ X X • At A 1: B 1 = B 2 • At A 2: B 1 = B 2 The effect of A doesn’t depend on level of B Examples of outcomes

B 1 A 2 Main Effect of B 60 60 60 B B 2 30 30 45 45 30 Dependent Variable A Main Effect of A Main effect of A X Main effect of B ✓ Interaction of A x B X B 1 B 2 A 1 A • At A 1: B 1 - B 2 = 30 • At A 2: B 1 - B 2 = 30 The effect of A doesn’t depend on level of B Examples of outcomes
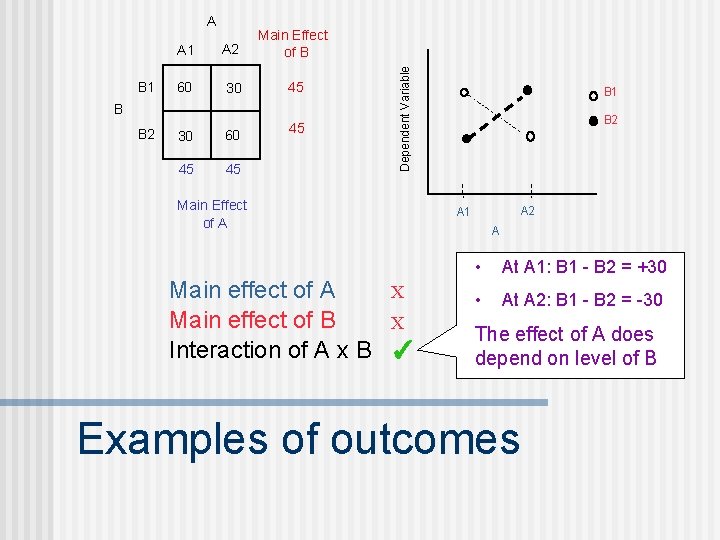
B 1 A 2 Main Effect of B 60 30 45 30 60 45 45 B B 2 45 Dependent Variable A Main Effect of A Main effect of A X Main effect of B X Interaction of A x B ✓ B 1 B 2 A 1 A • At A 1: B 1 - B 2 = +30 • At A 2: B 1 - B 2 = -30 The effect of A does depend on level of B Examples of outcomes
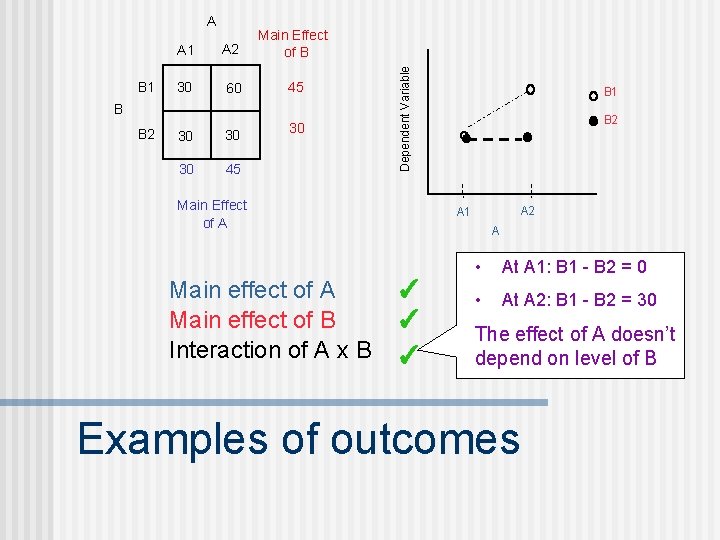
B 1 A 2 Main Effect of B 30 60 45 30 30 30 45 B B 2 30 Dependent Variable A Main Effect of A Main effect of B Interaction of A x B B 1 B 2 A 1 A ✓ ✓ ✓ • At A 1: B 1 - B 2 = 0 • At A 2: B 1 - B 2 = 30 The effect of A doesn’t depend on level of B Examples of outcomes
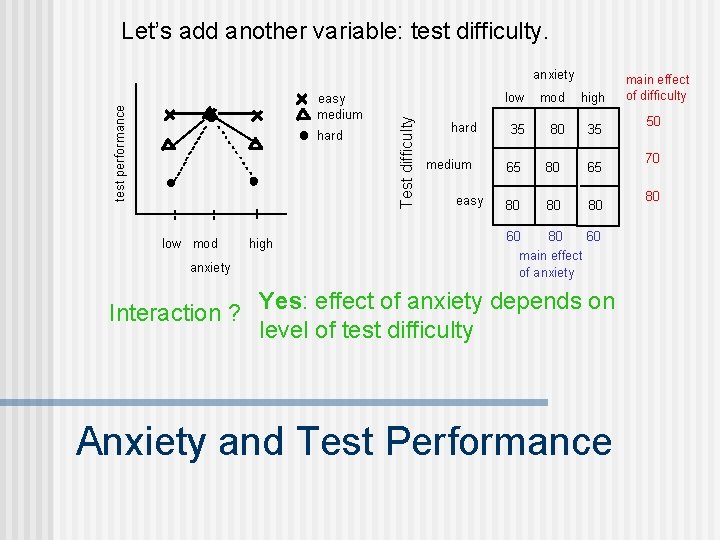
Let’s add another variable: test difficulty. test performance easy medium hard low mod anxiety high Test difficulty anxiety hard medium easy low mod high 35 80 35 65 80 80 80 60 main effect of anxiety Interaction ? Yes: effect of anxiety depends on level of test difficulty Anxiety and Test Performance main effect of difficulty 50 70 80

n Consider the results of our class experiment ✓ Main effect of word type n ✓ Main effect of depth of n processing ✓ An Interaction between n word type and depth of processing 1. 5 0. 7 Factorial designs Resource: Dr. Kahn's reporting stats page

n Advantages n Interaction effects – Consider the interaction effects before trying to interpret the main effects – Adding factors decreases the variability – Because you’re controlling more of the variables that influence the dependent variable – This increases the statistical Power of the statistical tests – Increases generalizability of the results – Because you have a situation closer to the real world (where all sorts of variables are interacting) Factorial Designs

n Disadvantages n n n Experiments become very large, and unwieldy The statistical analyses get much more complex Interpretation of the results can get hard • In particular for higher-order interactions • Higher-order interactions (when you have more than two interactions, e. g. , ABC). Factorial Designs

n n So far we’ve covered a lot of the about details experiments generally Now let’s consider some specific experimental designs. n n Some bad (but common) designs Some good designs • • 1 Factor, two levels 1 Factor, multi-levels Factorial (more than 1 factor) Between & within factors Experimental designs

n What is the effect of presenting words in color on memory for those words? n So you present lists of words for recall either in color or in black-and-white. Clock Chair Cab n Clock Chair Cab Two different designs to examine this question Example
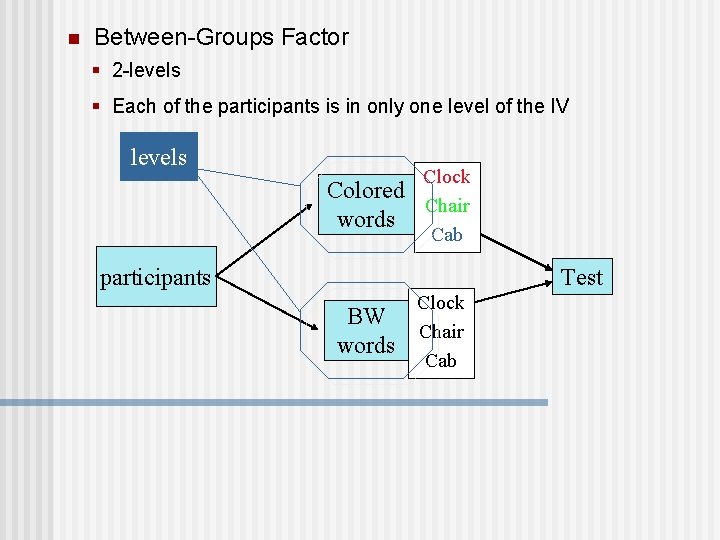
n Between-Groups Factor § 2 -levels § Each of the participants is in only one level of the IV levels Colored words Clock Chair Cab participants Test BW words Clock Chair Cab
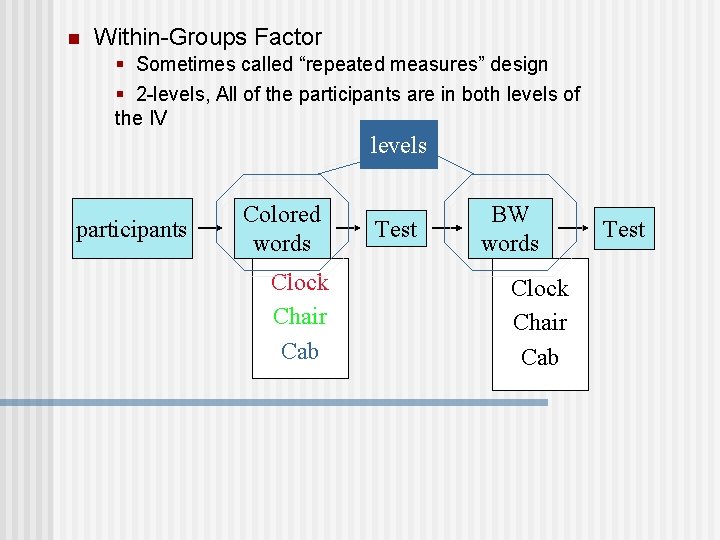
n Within-Groups Factor § Sometimes called “repeated measures” design § 2 -levels, All of the participants are in both levels of the IV levels participants Colored words Clock Chair Cab Test BW words Clock Chair Cab Test
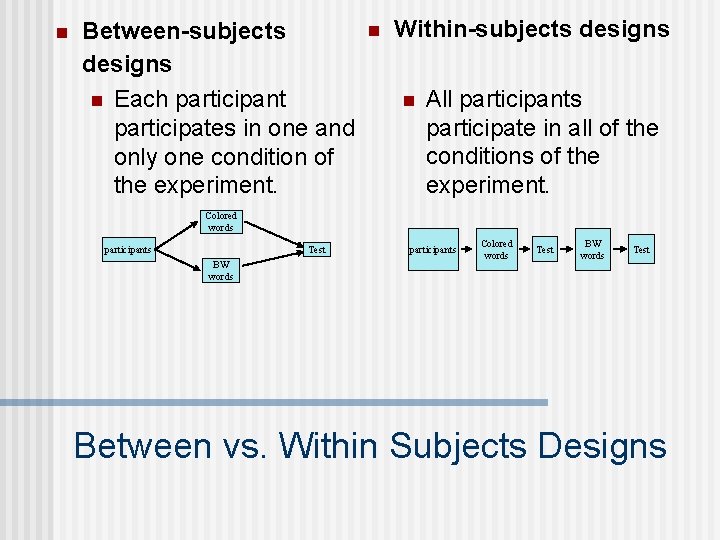
n Between-subjects designs n Each participant participates in one and only one condition of the experiment. n Within-subjects designs n All participants participate in all of the conditions of the experiment. Colored words Test participants BW words participants Colored words Test BW words Test Between vs. Within Subjects Designs
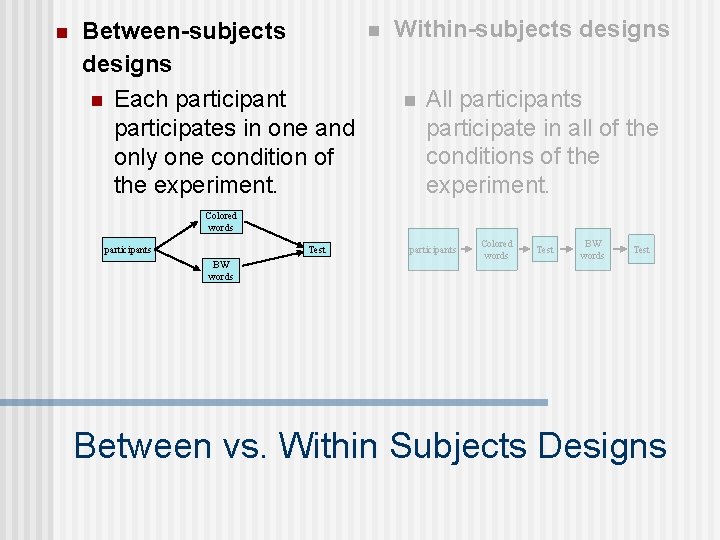
n Between-subjects designs n Each participant participates in one and only one condition of the experiment. n Within-subjects designs n All participants participate in all of the conditions of the experiment. Colored words Test participants BW words participants Colored words Test BW words Test Between vs. Within Subjects Designs
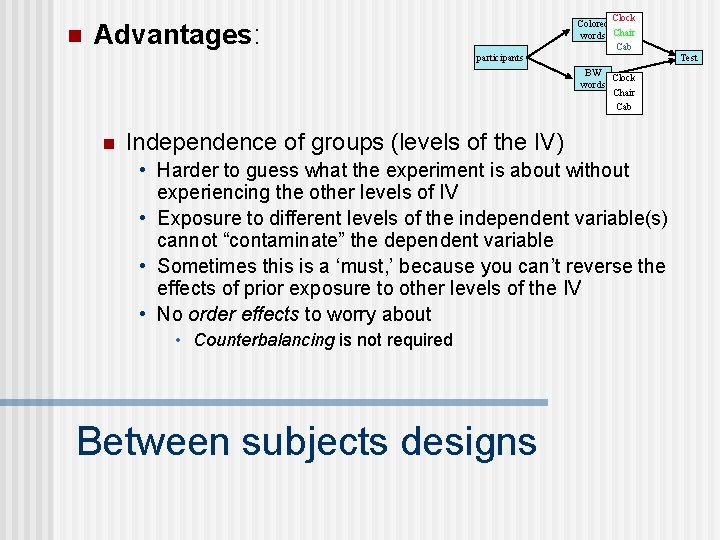
n Clock Colored words Chair Cab Advantages: Test participants BW Clock words Chair Cab n Independence of groups (levels of the IV) • Harder to guess what the experiment is about without experiencing the other levels of IV • Exposure to different levels of the independent variable(s) cannot “contaminate” the dependent variable • Sometimes this is a ‘must, ’ because you can’t reverse the effects of prior exposure to other levels of the IV • No order effects to worry about • Counterbalancing is not required Between subjects designs
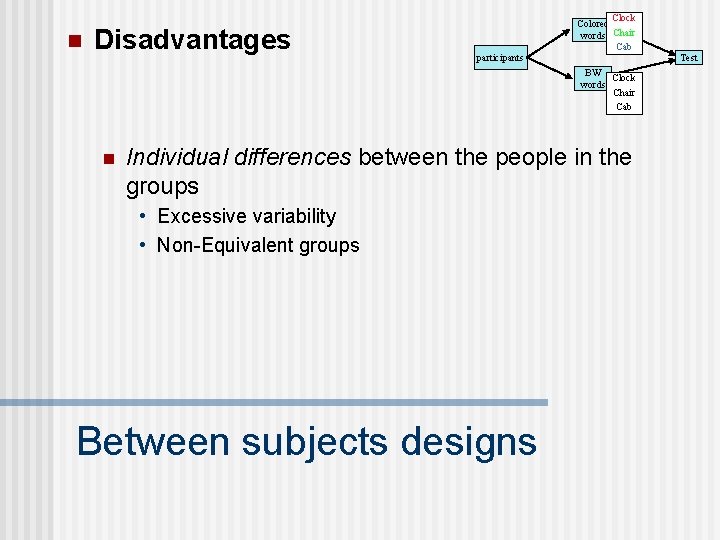
n Disadvantages Clock Colored words Chair Cab Test participants BW Clock words Chair Cab n Individual differences between the people in the groups • Excessive variability • Non-Equivalent groups Between subjects designs
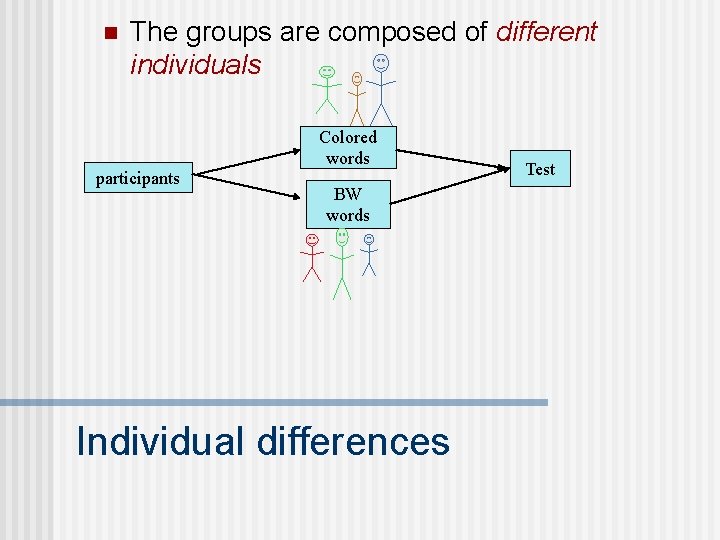
n The groups are composed of different individuals participants Colored words BW words Individual differences Test
n The groups are composed of different individuals participants n Colored words BW words Excessive variability due to individual differences n Test Harder to detect the effect of the IV if there is one Individual differences NR R R
n The groups are composed of different individuals participants n Colored words Test BW words Non-Equivalent groups (possible confound) n The groups may differ not only because of the IV, but also because the groups are composed of different individuals Individual differences

n Strive for Equivalent groups n n n Created equally - use the same process to create both groups Treated equally - keep the experience as similar as possible for the two groups Composed of equivalent individuals • Random assignment to groups - eliminate bias • Matching groups - match each individuals in one group to an individual in the other group on relevant characteristics Dealing with Individual Differences
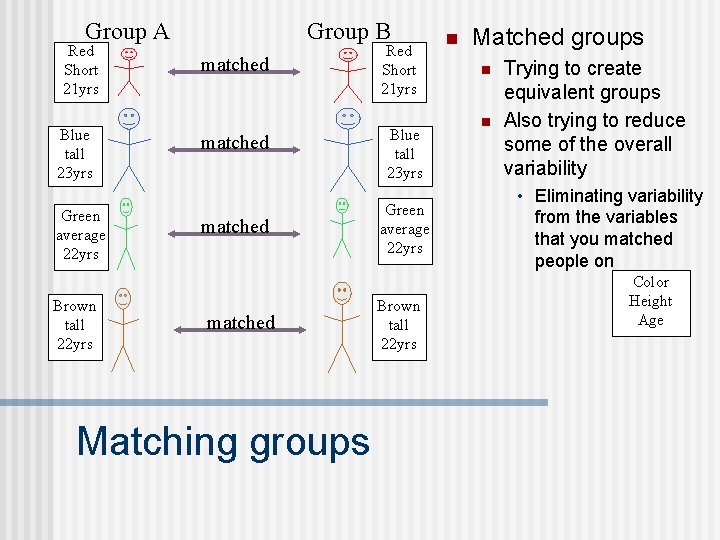
Group A Red Short 21 yrs Blue tall 23 yrs Green average 22 yrs Brown tall 22 yrs Group B matched Matching groups Red Short 21 yrs Blue tall 23 yrs Green average 22 yrs Brown tall 22 yrs n Matched groups n n Trying to create equivalent groups Also trying to reduce some of the overall variability • Eliminating variability from the variables that you matched people on Color Height Age

n Between-subjects designs n Each participant participates in one and only one condition of the experiment. n Within-subjects designs n All participants participate in all of the conditions of the experiment. Colored words Test participants Colored words Test BW words Between vs. Within Subjects Designs

n Advantages: n Don’t have to worry about individual differences • Same people in all the conditions • Variability between conditions is smaller (statistical advantage) n Fewer participants are required Within subjects designs

n Disadvantages n n Range effects Order effects: • Carry-over effects • Progressive error • Counterbalancing is probably necessary to address these order effects Within subjects designs

n Range effects – (context effects) can cause a problem n n The range of values for your levels may impact performance (typically best performance in middle of range). Since all the participants get the full range of possible values, they may “adapt” their performance (the DV) to this range. Within subjects designs

n Carry-over effects n n Transfer between conditions is possible Effects may persist from one condition into another • e. g. Alcohol vs no alcohol experiment on the effects on hand-eye coordination. Hard to know how long the effects of alcohol may persist. Condition 1 Condition 2 test Order effects How long do we wait for the effects to wear off? test

n Progressive error n n Practice effects – improvement due to repeated practice Fatigue effects – performance deteriorates as participants get bored, tired, distracted Order effects

n Counterbalancing is probably necessary n This is used to control for “order effects” • Ideally, use every possible order • (n!, e. g. , AB = 2! = 2 orders; ABC = 3! = 6 orders, ABCD = 4! = 24 orders, etc ). n All counterbalancing assumes Symmetrical Transfer • The assumption that AB and BA have reverse effects and thus cancel out in a counterbalanced design Dealing with order effects

n Simple case n n Two conditions A & B Two counterbalanced orders: • AB • BA Colored words Test BW words Test Colored words Test participants Counterbalancing

n Often it is not practical to use every possible ordering n Partial counterbalancing • Latin square designs – a form of partial counterbalancing, so that each group of trials occur in each position an equal number of times Counterbalancing

n Example: consider four conditions Recall: ABCD = 4! = 24 possible orders 1) Unbalanced Latin square: each condition appears in each position (4 orders) n Order 1 A B C D Order 2 Order 3 B C D A B Order 4 D A B C Partial counterbalancing

n Example: consider four conditions Recall: ABCD = 4! = 24 possible orders 2) Balanced Latin square: each condition appears before and after all others (8 orders) n A B C D A B D C B C D A B C A D C D A B C D B A D A B C D A C B Partial counterbalancing

n Mixed factorial designs n n Treat some factors as within-subjects (participants get all levels of that factor) and others as between-subjects (each level of this factor gets a different group of participants). This only works with factorial (multi-factor) designs Mixed factorial designs
- Slides: 44