Fractional Factorial Designs 27 Factorial Design in 8

Fractional Factorial Designs 27 – Factorial Design in 8 Experimental Runs to Measure Shrinkage in Wool Fabrics J. M. Cardamone, J. Yao, and A. Nunez (2004). “Controlling Shrinkage in Wool Fabrics: Effective Hydrogen Peroxide Systems, ” Textile Research Journal, Vol. 74 pp. 887 -898

Fractional Factorial Designs • For large numbers of treatments (k), the total number of runs for a full factorial can get very large (2 k) • Many degrees of freedom are spent on high-order interactions (which are often pooled into error with marginal gain in added degrees of freedom) • Fractional factorial designs are helpful when: § High-order interactions are small/ignorable § We wish to “screen” many factors to find a small set of important factors, to be studied more thoroughly later § Resources are limited • Mechanism: Confound full factorial in blocks of “target size”, then run only one block

Fractioning the 2 k - Factorial 2 k can be run in 2 q block of size 2 k-q for q=, 1…, k-1 2 k-q factorial is design with k factors in 2 k-q runs 1 Block of a confounded 2 k factorial Principal Block is called the principal fraction, other blocks are called alternate fractions • Procedure: • • Augment table of 2 -series with column of “+”, labeled “I” Defining contrasts are effects to be confounded together Generators are used to create the blocks by +/- structure Generalized Interactions of Generators also have constant sign in blocks § Defining Relations: I = A, I = -B I = -AB § §

Example – Wool Shrinkage • 7 Factors 27 = 128 runs in full factorial § § § § A = Na. OH in grams/litre (1 , 3) B = Liquor Dilution Ratio (1: 20, 1: 30) C = Time in minutes (20 , 40) D = GA in grams/litre (0 , 1) E = DD in grams/litre (0 , 3) F = H 2 O 2 (0 , 20 ml/L) G = Enzyme in percent (0 , 2) Response: Y = % Weight Loss • Experiment: Conducted in 2 k-q = 8 runs (1/16 fraction) • Need 24 -1 Defining Contrasts/Generalized Interactions § 4 Distinct Effects, 6 multiples of pairs, 4 triples, 1 quadruple

Defining Relations • I = ADEG = BDFG = ACDF = -BCF • Generalized Interactions: § § § (ADEG)(BDFG)=ABEF, (ADEG)(ACDF)=CEFG, (ADEG)(-BCF)=-ABCDEFG (BDFG)(ACDF)=ABCG, (BDFG)(-BCF)=-CDG, (ACDF)(-BCF)=-ABD (ADEG)(BDFG)(ACDF)=BCDE, (ADEG)(BDFG)(-BCF)=-ACE (ADEG)(ACDF)(-BCF)=-BEG, (BDFG)(ACDF)(-BCF)=-AFG (ADEG)(BDFG) (ACDF)(-BCF)=-DEF • Goal: Choose block where ADEG, BDFG, ACDF are “even” and BCF is “odd”. All other generalized interactions will follow directly

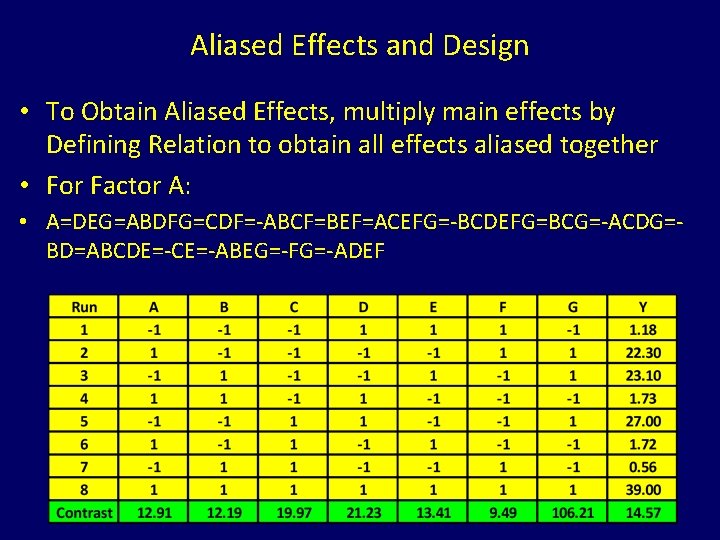
Aliased Effects and Design • To Obtain Aliased Effects, multiply main effects by Defining Relation to obtain all effects aliased together • For Factor A: • A=DEG=ABDFG=CDF=-ABCF=BEF=ACEFG=-BCDEFG=BCG=-ACDG=BD=ABCDE=-CE=-ABEG=-FG=-ADEF