Chapter 20 ValueatRisk Va R Paul Koch 1
































- Slides: 40

Chapter 20. Value-at-Risk (Va. R) © Paul Koch 1 -1 I. Motivation: A. Option sensitivities like delta, gamma, vega, . . . , describe different aspects of risk for a portfolio. 1. Banks typically compute each of these measures every day for each of the market variables they are exposed to. Traders & managers for the firm must know their situation. 2. There may be hundreds of these market variables. This analysis leads to huge number of risk measures each day. -- too much information for senior management to use.

I. B. Definition of Va. R © Paul Koch 1 -2 1. Va. R is an attempt to provide a single number that summarizes the total risk in a portfolio of financial assets. 2. Va. R aims to make a statement of the following form: “We are X% certain that we will not lose more than V dollars in the next N days. ” 3. Easy to understand. Simply asks, how bad can things get? 4. The variable, V, is the Va. R of the portfolio. V is a function of two parameters: N, the time horizon; X, the confidence level. 5. ES = Expected Shortfall = expected loss during N-day period, conditional on loss being worse than the Va. R loss. Va. R asks, “How bad can things get? ” ES asks, “If things get that bad, how much do we expect to lose? ”

I. C. Regulators Require Va. R for Banks © Paul Koch 1 -3 1. Calculation of Va. R was made easier in Oct. 1994, when J. P. Morgan made its Risk. Metrics database of volatilities and correlations freely available to all market participants. 2. The REGULATORS require Financial Institutions to use Va. R. e. g. , Banks are now required to calculate Va. R; Regulators use Va. R in determining required capital for a bank, to reflect the market risk it is bearing. 3. Bank regulators use N=10 and X=99; They consider losses over a 10 -day period that are expected only 1% of the time.

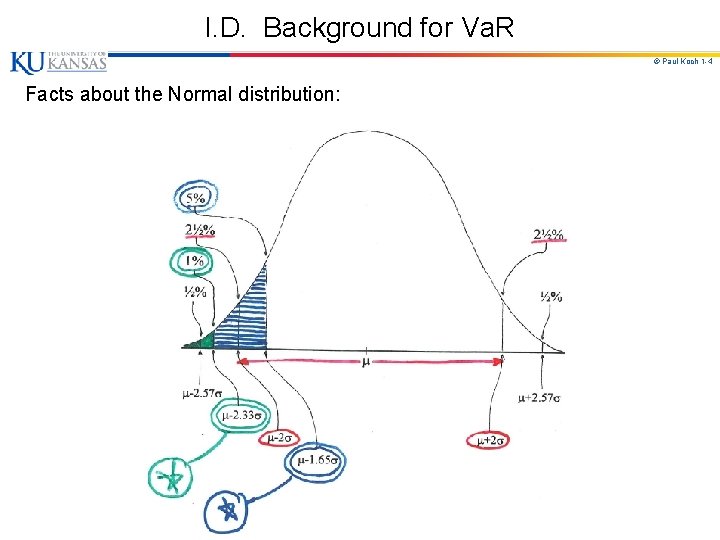
I. D. Background for Va. R © Paul Koch 1 -4 Facts about the Normal distribution:

II. Volatilities © Paul Koch 1 -5 A. The risk that a portfolio will lose value depends on the volatilities of the market variables it is exposed to. These volatilities play a key role in determining Va. R. B. Definition. 1. Recall definition of volatility for B / S model: σ = std dev of continuously compounded return in ONE YEAR. T ½ = std dev of continuously compounded return earned in time T. ** The “Square Root Effect”: uncertainty increases as a function of sqrt(T). 2. In Va. R calculations, T is measured in DAYS, so σ is "volatility per day. " σday = std dev of continuously compounded return in ONE DAY, = std dev of proportional change in asset price in ONE DAY. a. Note: σday σyear / (252) ½ ; there are 252 trading days in one year. Thus, σday σyear (. 06).

II. C. Estimating Volatility © Paul Koch 1 -6 1. Define σn = volatility per day ( σday ) for market variable, calculated on day n. Thus, σn 2 = variance rate of the market variable on day n. 2. Standard approach: Estimate HISTORICAL VOLATILITY. Let { S 1, S 2, . . . , Sn } be daily closing prices. Let ui = ln ( Si / Si-1 ) = daily returns. Then σn 2 = 1 / (n-1) Σ ( ui - mean(u) )2 Or, use approximation: Let mean(u) = 0; then σn 2 = 1/n Σui 2. [ Mean daily return ≈ 0; This is simple, & gives good approximation. ]

II. C. Estimating Volatility © Paul Koch 1 -7 3. Alternative approach: EWMA (Exponentially Weighted Moving Avg). a. The sample variance in 2. weights all ui 2 terms equally (same weight on day 1 or day n). EWMA weights ui 2 terms less if they are further back in time. Result: σn 2 = λ σn-12 + (1 - λ) un 2 (0 < λ < 1). b. Note 1: If you substitute successively for σn-12, σn-22, . . . , you can see that σn 2 depends on sum of past ui 2 terms, where weights decline exponentially : 1 st: Result is also true in period n-1: --- σn-12 = λ σn-22 + (1 -λ) un-12. Thus: σn 2 = λ (λσn-22 + (1 -λ)un-12) + (1 -λ) un 2 = λ 2 σn-22 + (1 -λ) [ λ un-12 + un 2 ]. 2 nd: Result is also true in period n-2: --- σn-22 = λ σn-32 + (1 -λ) un-22. Thus: σn 2 = λ 2 (λσn-32 + (1 -λ)un-22) + (1 -λ) [ λ un-12 + un 2 ] = λ 3 σn-32 + (1 -λ) [ λ 2 un-22 + λ un-12 + un 2 ]. kth: After k such substitutions, λk ≈ 0, so we get : σn 2 = λk σn-k 2 + (1 -λ) [ un 2 + λ un-1 + λ 2 un-22 + … + λk un-k 2 ] or σn 2 ≈ 0 + (1 -λ) [ un 2 + λ un-1 + λ 2 un-22 + … + λk un-k 2 + … ].

II. C. Estimating Volatility © Paul Koch 1 -8 More on EWMA: n 2 = n-12 + (1 - ) un 2 3. c. Example: Let λ =. 9, σn-1 =. 01, and un =. 02; Then σn 2 = (. 9)(. 0001) + (. 1)(. 0004) = . 00013 and σn = . 0114 Note: In this example, return on day n (un =. 02) > σn-1 (=. 01). Thus, when we add un 2 to get our new estimate, this increases σn. If, instead, un < σn-1, this would decrease σn. Thus, updated estimates of σn depend greatly on recent un. Note 1: EWMA approach can be updated easily each day. Simply keep current estimate of σn-1, & consider the new daily return, un. Note 2: EWMA approach succeeds in tracking changes in volatility; If true σn 2 ↑ over time, the values for ui 2 will also ↑, so σn 2 will ↑. Note 3: λ determines how responsive σn 2 is to changes in ui 2. Low value of λ means ui 2 terms further back mean less; recent ui 2 more. High value of λ means ui 2 terms further back mean more; recent ui 2 less.

III. Correlations © Paul Koch 1 -9 A. Intuition: The risk that a portfolio will lose value also depends on the correlations among the market variables it is exposed to. 1. Suppose portfolio is exposed to risk that both Euro & Yen will ↓. We should consider whether these exchange rates are correlated! i. e. , If Euro ↓, does Yen also tend to ↓? B. Definition. 1. Consider two market variables, U & V (returns/changes in 2 prices). Let: σu, n = daily volatility of variable U, calculated on day n; σv, n = daily volatility of variable V, calculated on day n; covn = covariance between daily returns, U & V, on day n. Then ρuv = covn / σu, n σv, n.

III. C. Estimating Correlations © Paul Koch 1 -10 1. Historical correlation measures -- equally weighted ui and vi: Let Then: mean(u) = mean(v) = 0; σu, n 2 = 1/n Σ ui 2 ; σv, n 2 = 1/n Σ vi 2; covn = 1/n Σ ui vi. Note: This formula gives equal weights to all ui vi terms in covn. 2. EWMA: covn = λ covn-1 + (1 -λ) un vn. Note: Weights on ui vi terms decline as we move back in time. The lower the value of λ, the less weight on older terms, and the more weight is placed on recent observations. Note: Must be consistent how you treat σu, n 2, σv, n 2, and covn. If you get σu, n 2 & σv, n 2 with equal (declining) weights, must also get covn with equal (declining) weights.

IV. Simple Example © Paul Koch 1 -11 A. Portfolio 1 consists of $10, 000 in IBM stock (U); Daily Volatility = σu, n = . 02 (corresponds to annual Vol of . 02 (252)½ =. 32); Compute the Va. R of this portfolio. Let N = 10 days, X = 99. Std Dev of change in IBM pf over 1 day = $10, 000 (. 02) = $200, 000. Std Dev of change in IBM pf over 10 days = $10, 000 (. 02) (10½ ) = $200, 000 (10½) = $632, 456. Assume 1: mean(U) = 0. This expected return is likely small relative to Std Dev. e. g. , if E(r) over 1 year = 18%, then E(r) over 1 day = 18% / 252 =. 07% [ much < 1 -day σu, n = 2% ]; Assume 2: U is normally distributed (i. e. , S is lognormal). Then there is 99% chance S will not decrease more than 2. 33 std dev. (Or a 95% chance S will not decrease more than 1. 65 std dev). THUS, the 99% / 10 -day Va. R is 2. 33 x $632, 456 = $1, 473, 621; Or, the 95% / 10 -day Va. R is 1. 65 x $632, 456 = $1, 043, 552. 99% sure won’t lose > $1, 473, 621 in 10 days; 95% sure won’t lose > $1, 043, 552 in 10 days.

IV. Simple Example © Paul Koch 1 -12 B. Portfolio 2 consists of $5, 000 of AT&T stock (V); Daily Volatility = σv, n = . 01 (corresponds to annual Vol of . 01 (252)½ =. 16); Std Dev of change in AT&T pf over 10 days = $5, 000 x. 01 x (10 ½ ) = $158, 144 The 99% / 10 -day Va. R for this portfolio is: 2. 33 x $158, 144 = $368, 405; The 95% / 10 -day Va. R for this portfolio is: 1. 65 x $158, 144 = $260, 937. [ Less Value-at-Risk than Portfolio 1! ] C. Portfolio 3 = Portfolio 1 + Portfolio 2. In addition, suppose we know ρuv =. 7 We need the Std Dev of the value of this portfolio, U + V. In general, σ(U + V) = [ σU 2 + σV 2 + 2 ρ σU σV ] ½ For this example, we have σU = $632, 456, and σV = $158, 114. Thus, σ(U + V) = [ $632, 4562 + $158, 1142 + 2 (. 7) (632, 456) (158, 144) ] ½ = $751, 665 Then: 99% / 10 -day Va. R for Portfolio 3 is 2. 33 x $751, 665 = $1, 751, 379 Or: 95% / 10 -day Va. R for Portfolio 3 is 1. 65 x $751, 665 = $1, 240, 247

IV. Simple Example © Paul Koch 1 -13 D. The Benefits of Diversification. If changes in value of IBM & AT&T were perfectly correlated (ρ = 1), Va. R of Portfolio 3 = Va. R of Portfolio 1 + Va. R of Portfolio 2. If IBM and AT&T have correlation < 1, (ρ < 1), Va. R of Portfolio 3 < Va. R of Portfolio 1 + Va. R of Portfolio 2. HERE, ρ =. 7; Va. R for Portfolio 1 (U) = $1, 473, 621; Va. R for Portfolio 2 (V) = $368, 405; Va. R for Portfolio 3 (U + V) = $1, 751, 379. Benefits of Diversification = [ Va. R(U) + Va. R(V) ] - Va. R(U + V) = [ $1, 473, 621 + $368, 405 ] - $1, 751, 379 = $90, 647 This exercise shows that lower correlation means lower Va. R.

V. Linear Model © Paul Koch 1 -14 A. Va. R calculations are straightforward when (like in above example): 1. We assume that change in value of portfolio is linearly related to the changes in values of underlying market variables; 2. The changes in values of underlying market variables are normal. B. General Linear Model (GLM): Assume there are n underlying market variables; n ΔP = Σ αi Δxi i=1 where ΔP = $-change in portfolio value in one day; Δxi = prop. change (return) on underlying ith market variable during day; αi = constants. Define: σi = daily volatility of Δxi; ρij = correlation between Δxi and Δxj. n Then σp = daily volatility of ΔP, where σP 2 = Σ αi 2 σi 2 + 2 Σ Σ αi αj σi σj ρij. i=1 i<j

V. B. General Linear Model © Paul Koch 1 -15 1. Redo previous example; n = 2 assets in Portfolio 3; Δx 1 & Δx 2 are prop. changes in prices of IBM & AT&T in 1 day; Measuring values in millions of $, ΔP = 10Δx 1 + 5Δx 2 [α 1 = 10; α 2 = 5] Also given: σ1 =. 02; σ2 =. 01; ρ12 =. 7; Then and σP 2 = 102 x. 022 + 52 x. 012 + 2 x 10 x 5 x. 02 x. 01 x. 7 = . 0565 σP = . 238 = std dev of change in portfolio value per day; Then and σP (10) ½ = . 238 (10) ½ = . 752 = std. dev. of ΔP over 10 days, 99% / 10 -day Va. R = 2. 33 x. 752 = $1. 751 million (same answer).

V. C. When Linear Model can be Used © Paul Koch 1 -16 1. When the payoff patterns of the assets in the portfolio are linear. a. Examples: i. Portfolio with no derivatives (stocks, bonds, foreign exchange, & commodities). Here ΔP is linearly dependent on the Δxi (changes in the underlying prices). ii. Portfolio with certain derivatives having linear payoff patterns. e. g. 1 Forward contract to buy foreign currency maturing at T. This can be regarded as exchange of a foreign zero-coupon bond for a domestic zero-coupon bond, both maturing at time T. Therefore, we can rewrite this portfolio as linear combination of positions in bonds and foreign exchange, as in i. , and ΔP depends linearly on zero-coupon bond prices and exchange rates. e. g. 2 Interest rate SWAP. This can be regarded as exchange of a floating rate bond for a fixed rate bond. The fixed rate bond can be regarded as a portfolio of zero-coupon bonds. The floating rate bond will be worth par just after next payment. Thus the interest rate SWAP reduces to a portfolio of long and short positions in zero-coupon bonds.

V. D. Options have Nonlinear Payoffs © Paul Koch 1 -17 Thus, linear model only holds approximately when portfolio contains options. 1. Explanation: Consider portfolio of options on a single stock. δ = ΔP / ΔS; or ΔP = δ ΔS where ΔS is the $ change in the stock price in 1 day. Define Δx as the proportional change (return) in the stock price in 1 day: Δx = ΔS / S; or S = S x Then an approximate relationship between ΔP and Δx is: ΔP = δ ΔS; or ΔP = S x = S x. When we have position in several market variables that includes options, we can derive approximately linear relation between ΔP & Δxi's similarly: n ΔP = Σ Si δi Δxi ; where Si = price of ith market variable; i=1 and δ = delta of pf wrt ith mkt variable. i n This corresponds to old GLM equation: ΔP = Σ αi Δxi with αi = Si δi. i=1

V. D. Options have Nonlinear Payoffs © Paul Koch 1 -18 2. Example. Consider portfolio of options on IBM and AT&T. Let δ 1 = 1, 000 = delta of IBM option position; = (∆P 1 / ∆S 1) δ 2 = 20, 000 = delta of AT&T option position; = (∆P 2 / ∆S 2) S 1 = $120 = share price of IBM; S 2 = $30 = share price of AT&T; σ1 = . 02 = volatility of IBM price changes in one day; σ2 = . 01 = volatility of AT&T price changes in one day. (S 1) ( 1) (S 2) ( 2) As an approximation: ΔP = 120 x 1, 000 Δx 1 + 30 x 20, 000 Δx 2 or ΔP = 120, 000 Δx 1 + 600, 000 Δx 2 where Δx 1 & Δx 2 are prop. changes in prices of IBM & AT&T in 1 day, and ΔP is the resulting change in the portfolio. Then the Std Dev of ΔP in one day (in thousands of $) is: [ (120 x. 02)2 + (600 x. 01)2 + 2 x 120 x. 02 x 600 x. 01 x. 7 ] ½ = 7. 689 Thus the 95% / 5 -day Va. R is: 1. 65 x (5) ½ x 7, 869 = $29, 033.

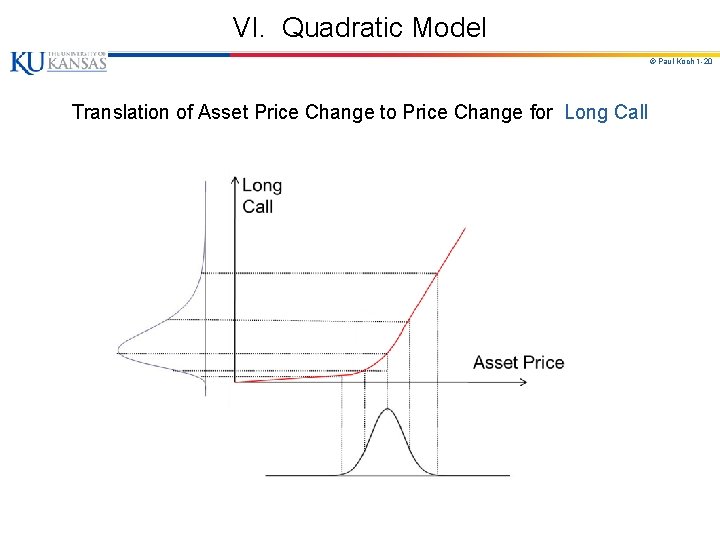
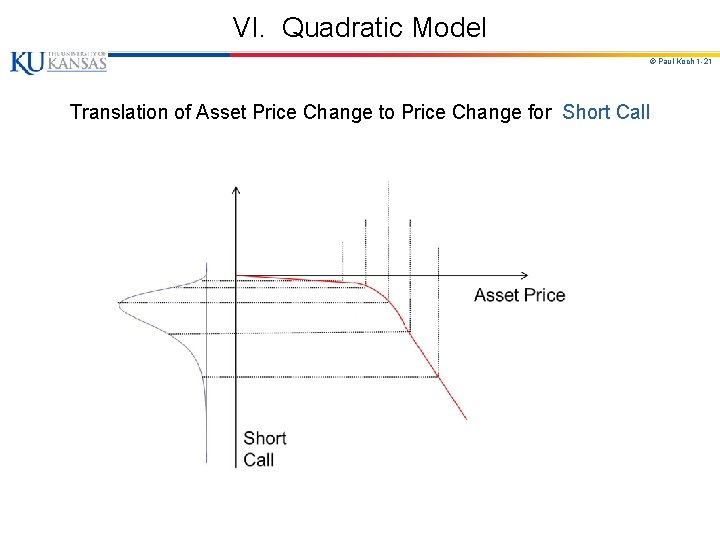
VI. Quadratic Model © Paul Koch 1 -19 Motivation: When Portfolio includes options, the linear model is only an approximation -- it ignores gamma, or curvature. A. Impact of gamma ( ) on the probability distribution of ΔP. (Fig. 20. 3 on top; Fig. 20. 4, 20. 5 on bottom. ) 1. When > 0 (long options) distrib skewed right. When < 0 (short options) distrib skewed left. a. Payoff pattern on long call option ( > 0). If underlying market variable is normal, implied distribution is skewed to right. b. Payoff pattern on short call option ( < 0). If underlying market variable is normal, implied distribution is skewed to left.

VI. Quadratic Model © Paul Koch 1 -20 Translation of Asset Price Change to Price Change for Long Call

VI. Quadratic Model © Paul Koch 1 -21 Translation of Asset Price Change to Price Change for Short Call

VI. B. Va. R of Portfolio depends on Left Tail for ΔP © Paul Koch 1 -22 99% Va. R is value below which is only 1% of distribution (left tail). 95% Va. R is value below which is only 5% of distribution (left tail). 1. Positive gamma portfolio is skewed to right; Has thin left tail & fat right tail (less downside). Thus, if you assume distribution of ΔP is normal, Va. R too large; true left tail thinner than normal; Area under thin left tail is less than that under normal; so normal Va. R suggests bigger loss than reality; should go less far left. 2. Negative gamma portfolio is skewed to left; Has fat left tail & thin right tail (more downside). Thus, if you assume distribution of ΔP is normal, Va. R too small; true left tail fatter than normal; Area under fat left tail is more than that under normal; so normal Va. R suggests smaller loss than reality; should go farther left.

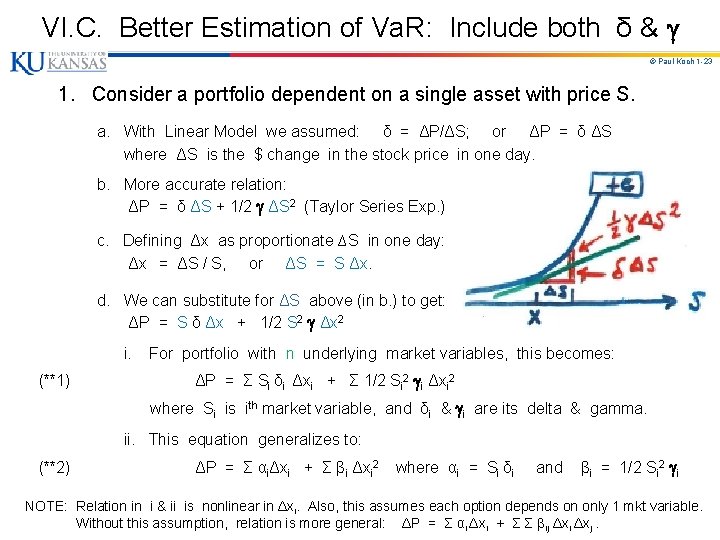
VI. C. Better Estimation of Va. R: Include both δ & © Paul Koch 1 -23 1. Consider a portfolio dependent on a single asset with price S. a. With Linear Model we assumed: δ = ΔP/ΔS; or ΔP = δ ΔS where ΔS is the $ change in the stock price in one day. b. More accurate relation: ΔP = δ ΔS + 1/2 ΔS 2 (Taylor Series Exp. ) c. Defining Δx as proportionate ∆S in one day: Δx = ΔS / S, or ΔS = S Δx. d. We can substitute for ΔS above (in b. ) to get: ΔP = S δ Δx + 1/2 S 2 Δx 2 i. For portfolio with n underlying market variables, this becomes: (**1) ΔP = Σ Si δi Δxi + Σ 1/2 Si 2 i Δxi 2 where Si is ith market variable, and δi & i are its delta & gamma. ii. This equation generalizes to: (**2) ΔP = Σ αiΔxi + Σ βi Δxi 2 where αi = Si δi and βi = 1/2 Si 2 i NOTE: Relation in i & ii is nonlinear in Δxi. Also, this assumes each option depends on only 1 mkt variable. Without this assumption, relation is more general: ΔP = Σ αi Δxi + Σ Σ βij Δxi Δxj.

VI. C. Better Estimation of Va. R: Include both δ & © Paul Koch 1 -24 2. Problem: This nonlinear model is not as easy to work with. Can be used with Simulation Approach (more later). a. Nonlinear Equation (**2) can be used to calculate moments for ΔP: n E(ΔP) = Σ βi σi 2 ; since E(Δxi) = 0; i=1 n n E(ΔP 2) = Σ Σ [ αi αj σi σj ρij + βi βj σi 2 σj 2 (1 + 2 ρij 2 ) ] i=1 j=1 b. These moments can be fitted to a normal distribution. (However, once again, assumption of normality is not great. ) c. Can also calculate higher moments of ΔP (skewness, kurtosis). Higher moments can then be used with the Cornish-Fisher expansion to estimate the fractiles of the probability distribution of ΔP that correspond to any required Va. R.

VII. Monte Carlo Simulation © Paul Koch 1 -25 A. Alternative approach: Use Simulation to get probability distrib. for ΔP. To calculate a one-day Va. R for a portfolio: 1. Value the portfolio today, using current values of market variables. 2. Sample once from multivariate normal probability distrib. of Δxi's. (Pick parameters -- moments -- of distrib. as desired. See VI. C. 2. ) 3. Use values of Δxi's that are sampled to determine simulated new value of each market variable at end of the day. 4. Revalue portfolio at end of the day using the new sampled values. 5. Subtract value in step 1 from that in step 4 to get sample ΔP. 6. Repeat steps 2 - 5 many times to build probability distrib. for ΔP.

VII. Monte Carlo Simulation © Paul Koch 1 -26 B. Va. R is computed as proper fractile of probability distrib. of ΔP. 1. For example, calculate 5, 000 sample values for ΔP. The 99% / 1 -day Va. R is value of ΔP for 50 th worst outcome; The 95% / 1 -day Va. R is value of ΔP for 250 th worst outcome; … The N-day Va. R is then calculated as the 1 -day Va. R times (N)½. 2. Drawback of simulation -- computationally intensive (no problem!). A company's complete portfolio (maybe thousands of assets) has to be revalued many times (step 4). a. Can speed procedure by assuming that equation (**2) describes the relation between ΔP and the Δxi's. (Can then skip steps 3 & 4 each iteration; no need to revalue the portfolio every time. )

VIII. Use of Historical Data © Paul Koch 1 -27 A. Can calculate Va. R from simulation based on historical mkt behavior. 1. First create a database consisting of daily movements in all market variables over several years. 2. First simulation trial lets the % changes in all market variables be those experienced on the first day in the database. 3. The second simulation . . . on the second day. And so on. 4. The change in portfolio, ΔP, is calculated for each simulation trial and Va. R is calculated as proper fractile of the prob. distrib. of ΔP. Here the change in portfolio value can be obtained either by revaluing, or by using equation (**2).

VIII. Use of Historical Data © Paul Koch 1 -28 B. Advantage: This accurately reflects historical distrib. of mkt variables. C. Disadvantages: 1. Number of simulation trials is limited to number of days in database. 2. Sensitivity analyses are difficult. (With statistical simulation, can change distrib. parameters & rerun. ) 3. Variables for which there are no mkt data cannot easily be included. D. Kurtosis. 1. For many mkt variables, the probability distrib of the Δxi and ΔP that is calculated from historical data often exhibits fat tails, so that extreme outcomes are more likely than normal distrib. . This is positive kurtosis. This can be modeled in the simulation. . .

IX. Stress Testing © Paul Koch 1 -29 A. Can examine how current portfolio would perform under the most extreme market moves seen in the last 10 to 20 years. 1. To test impact of extreme movement in U. S. stock market: a. Could let prop. change in all market variables (Δxi's) equal those on Oct. 19, 1987 (when S&P 500 changed 22. 3 std dev’s). b. Could use Δxi's on Jan. 8, 1988 (S&P 500 changed 6. 8 σ's). 2. To test impact of extreme movement in U. K. interest rates: a. Could use Δxi's on Apr 10, 1992 (10 -yr bond yield rose 7. 7 σ's).

IX. Stress Testing © Paul Koch 1 -30 B. A way to consider implications of extreme events that happen, but are almost impossible according to normal prob. distribution. 1. For example, under normal distribution, a change of 5σ's happens one day every 7, 000 years. In practice, we have seen this once or twice every 10 or so years. C. Simple to do. Once we have the variance of the in value of the portfolio over 1 -day, we can multiply this by any number of standard deviations desired, and then multiply by (N)½ to get N-day Va. R at any confidence level.

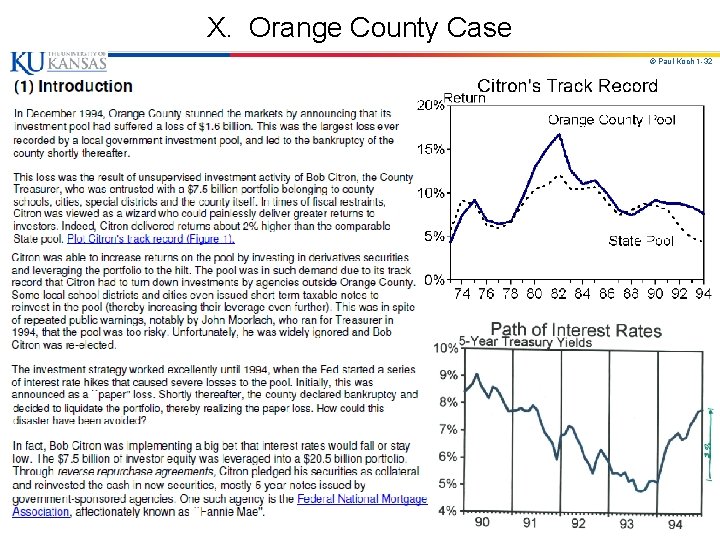
X. Orange County Case © Paul Koch 1 -31

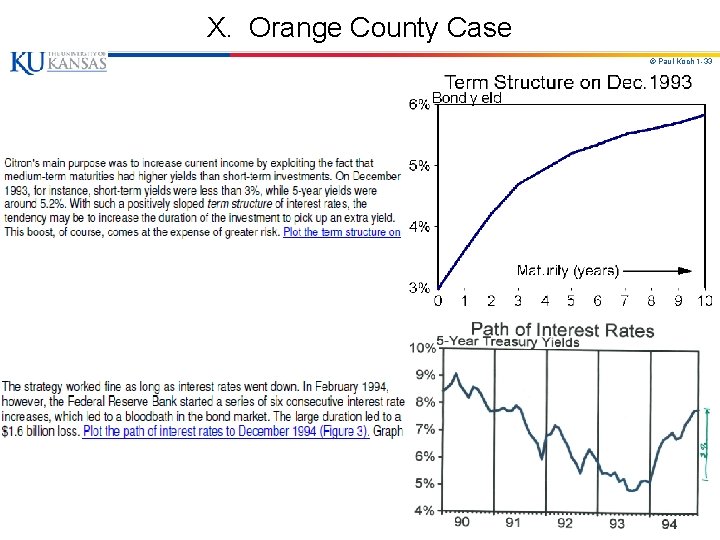
X. Orange County Case © Paul Koch 1 -32

X. Orange County Case © Paul Koch 1 -33

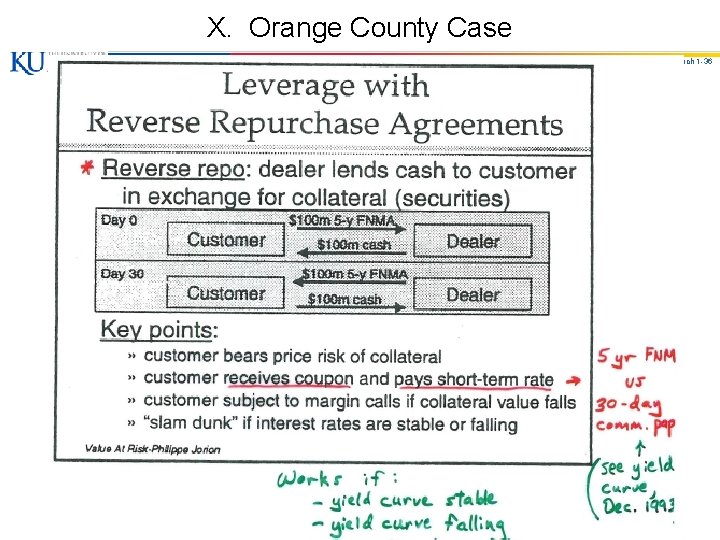
X. Orange County Case © Paul Koch 1 -34

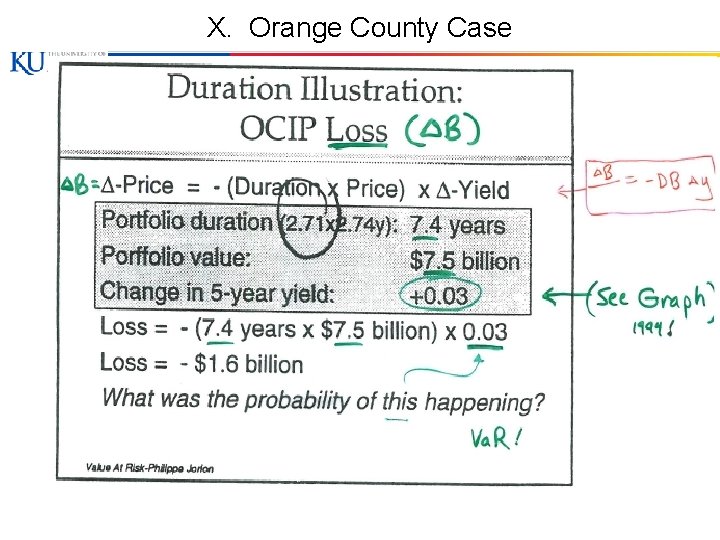
X. Orange County Case © Paul Koch 1 -35

X. Orange County Case © Paul Koch 1 -36

X. Orange County Case © Paul Koch 1 -37

X. Orange County Case © Paul Koch 1 -38

X. Orange County Case © Paul Koch 1 -39

© Paul Koch 1 -40