Chapter 2 Introduction to Logic and Sets Copyright

Chapter 2 Introduction to Logic and Sets Copyright © 2016, 2013, and 2010, Pearson Education, Inc.

2 -3 Other Set Operations and Their Properties Students will be able to understand explain • Relations between set operations and logic connectives. • Properties of set and logic operations. • Venn diagrams to sort and reason with data. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 2

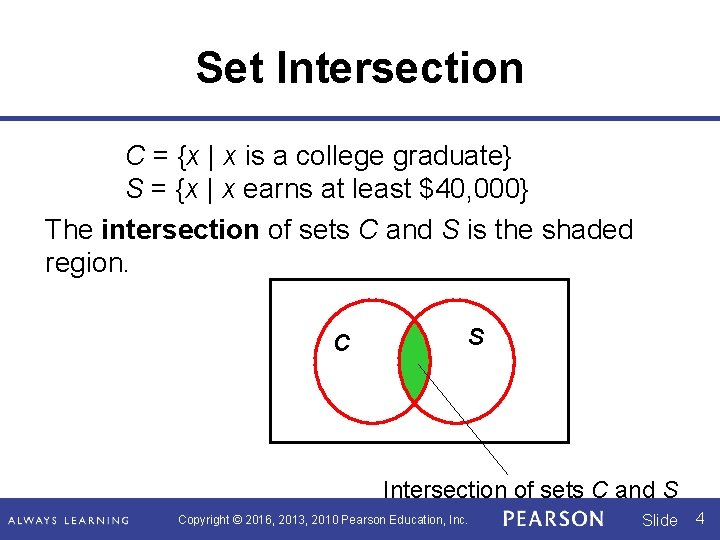
Set Intersection Consider the following sets: C = {x | x is a college graduate} S = {x | x earns at least $40, 000} Suppose we want to mail a questionnaire to all individuals in a certain city who are college graduates and who earn at least $40, 000. Then the individuals to receive the questionnaire include those common to both sets C and S. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 3

Set Intersection C = {x | x is a college graduate} S = {x | x earns at least $40, 000} The intersection of sets C and S is the shaded region. C S Intersection of sets C and S Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 4

Definition The intersection of two sets A and B, written is the set of all elements common to both A and B. The key word is “and” which implies both conditions must be met. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 5

Example Find a. b. (A and B are disjoint. ) c. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 6

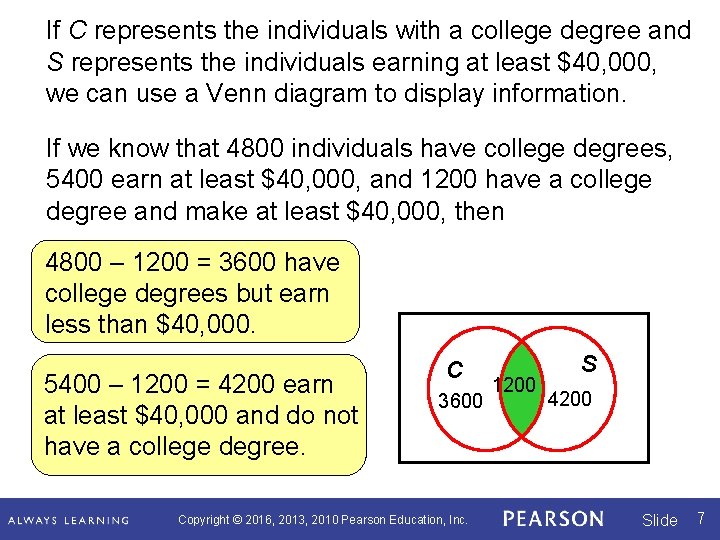
If C represents the individuals with a college degree and S represents the individuals earning at least $40, 000, we can use a Venn diagram to display information. If we know that 4800 individuals have college degrees, 5400 earn at least $40, 000, and 1200 have a college degree and make at least $40, 000, then 4800 – 1200 = 3600 have college degrees but earn less than $40, 000. 5400 – 1200 = 4200 earn at least $40, 000 and do not have a college degree. C 3600 Copyright © 2016, 2013, 2010 Pearson Education, Inc. 1200 S 4200 Slide 7

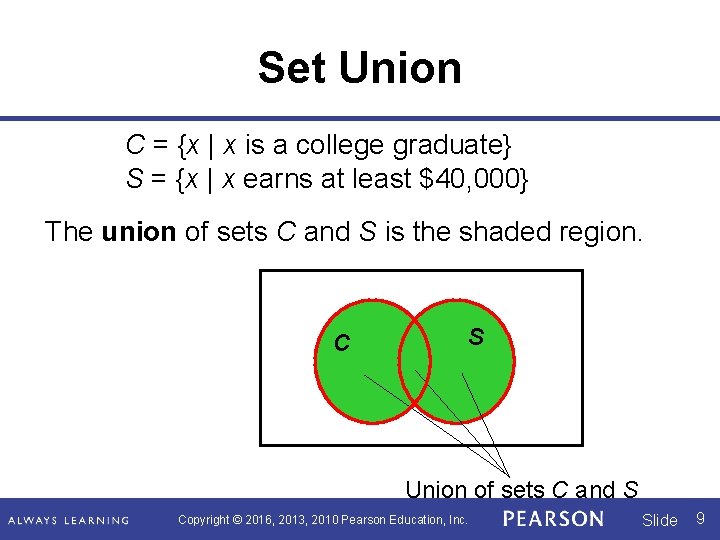
Set Union Consider the following sets: C = {x | x is a college graduate} S = {x | x earns at least $40, 000} Suppose we want to mail a questionnaire to all individuals in a certain city who are college graduates or who earn at least $40, 000, or both. Then the individuals to receive the questionnaire include those who are members of set C or set S. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 8

Set Union C = {x | x is a college graduate} S = {x | x earns at least $40, 000} The union of sets C and S is the shaded region. C S Union of sets C and S Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 9

Definition The union of two sets A and B, written is the set of all elements in A or in B. The key word is “or” which implies one or the other or both. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 10

Example Find a. b. c. since every element of A is in B. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 11

Set Difference Consider the following sets: C = {x | x is a college graduate} S = {x | x earns at least $40, 000} The set of individuals earning at least $40, 000 but not a college graduate is called the complement of C relative to S, or the set difference of S and C. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 12

Definition The complement of A relative to B, written B − A, is the set of all elements in B that are not in A. Note B − A that is not read as “B minus A. ” Minus is an operation on numbers and set difference is an operation on sets. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 13

Relative Complement A B This is the set of all elements in B and not in A. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 14

Example If find A − B, B − A, B − C, and C − B. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 15

Properties of Set Operations Commutative Properties For all sets A and B, Since the order of the elements in a set is not important, it does not matter in which order we write the sets when we find the union or the intersection. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 16

Properties of Set Operations Associative Properties For all sets A and B, Since the order of the elements in a set is not important, it does not matter in which way we associate sets when we take the union or the intersection. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 17

Distributive Property of Intersection Over Union For all sets A, B, and C, Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 18

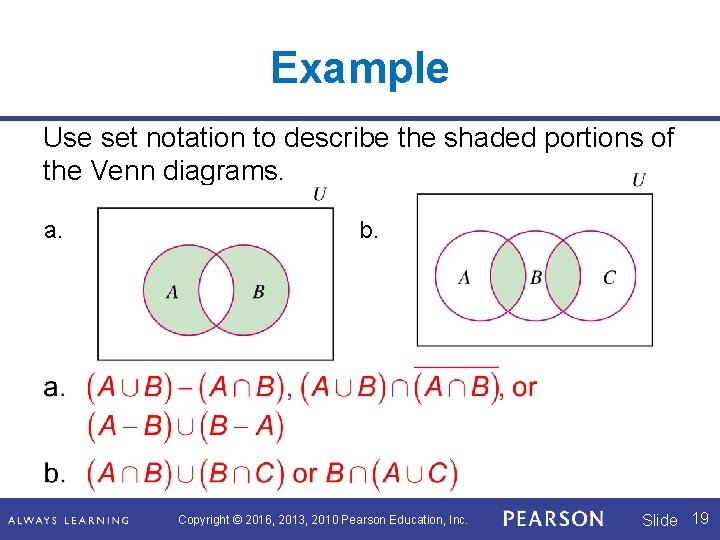
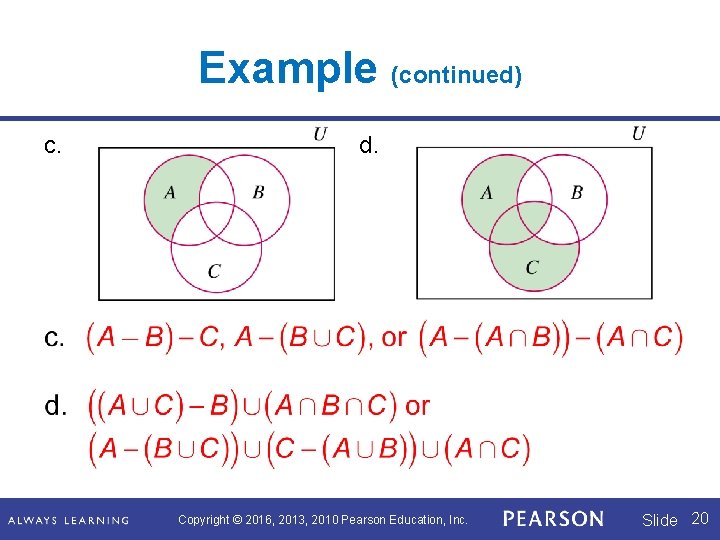
Example Use set notation to describe the shaded portions of the Venn diagrams. a. b. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 19

Example (continued) c. d. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 20

Example Suppose M is the set of all students taking mathematics and E is the set of all students taking English. Identify the students described by each region in the figure. Region (a) contains all students taking mathematics but not English or M – E. Region (b) contains all students taking both mathematics and English or Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 21

Example cont. Suppose M is the set of all students taking mathematics and E is the set of all students taking English. Identify the students described by each region in the figure. Region (c) contains all students taking English but not mathematics or E – M. Region (d) contains all students taking neither mathematics nor English or Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 22

Example In a survey that investigated the high school backgrounds of 110 college freshmen, the following information was gathered: 25 took physics 45 took biology 48 took mathematics 10 took physics and mathematics 8 took biology and mathematics 6 took physics and biology 5 took all three subjects. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 23

Example (continued) a. How many students took biology but neither physics nor mathematics? b. How many took physics, biology, or mathematics? c. How many did not take any of the three subjects? To solve this problem, we build a model using sets. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 24

Example (continued) P is the set of students taking physics, B is the set taking biology, and M is the set taking mathematics. The shaded region represents the 5 students who took all three subjects. The lined region represents the students who took physics and mathematics, but who did not take biology. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 25

Example (continued) The number of students who took biology but not physics or mathematics is represented by Because a total of 10 students took physics and mathematics and 5 of those also took biology, 10 − 5, or 5, students took physics and mathematics but not biology. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 26

Example (continued) Because 8 students took biology and mathematics and 5 took all three subjects, 8 − 5, or 3, took biology and mathematics but not physics. 6 − 5, or 1, student took physics and biology, but not mathematics. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 27

Example (continued) To find the number of students who took biology but neither physics nor mathematics, we subtract from 45 (the total number that took biology) the number of those that are in the distinct regions that include biology and other subjects, that is, 1 + 5 + 3, or 9. Because 45 − 9 = 36, we know that 36 students took biology, but neither physics nor mathematics. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 28

Example (continued) The number of students who took physics, biology, or mathematics is represented by The number of students who took physics but neither mathematics nor biology is 25 − (1 + 5), or 14. The number of students who took mathematics but neither physics nor biology is 48 − (5 + 3), or 35. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 29

Example (continued) The number of students who took physics, biology, or mathematics is 35 + 14 + 36 + 3 + 5 + 1, or 99. Because the total number of students is 110, the number that did not take any of the three subjects is 110 − 99, or 11. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 30

Cartesian Products One way to produce a set from two sets is by forming pairs of elements of one set with the elements of another set in a specific way. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 31

Cartesian Products Suppose a person has three pairs of pants, P = {blue, green, white}, and two shirts, S = {blue, red}. According to the Fundamental Counting Principle, there are 3 • 2 = 6 possible ways to pair an element from set P with an element from set S, forming a set of ordered pairs. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 32

Cartesian Products Because the first component in each pair represents pants and the second component in each pair represents shirts, the order in which the components are written is important. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 33

Definition Equality for ordered pairs: (x, y) = (m, n) if, and only if, the first components are equal and the second components are equal. A set consisting of ordered pairs is an example of a Cartesian product. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 34

Definition For any sets A and B, the Cartesian product of A and B, written A �B, is the set of all ordered pairs such that the first component of each pair is an element of A and the second component of each pair is an element of B. Note that A × B is commonly read as “A cross B” and should never be read “A times B. ” Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 35

Example If A = {a, b, c} and B = {1, 2, 3}, find each of the following: a. A × B b. B × A c. A × A a. A × B = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3)} b. B × A = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)} c. A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 36

Cartesian Products Is it possible to form a Cartesian product involving the null or empty set? Suppose A = {1, 2}. Because there are no elements in Ø, no ordered pairs (x, y) are possible with x A and y Ø, so A × Ø = Ø. Similarly, Ø × A = Ø for all sets A. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 37