CAPITULO 5 Cuadripolos Teora de Circuitos Hemos visto

CAPITULO 5 Cuadripolos Teoría de Circuitos

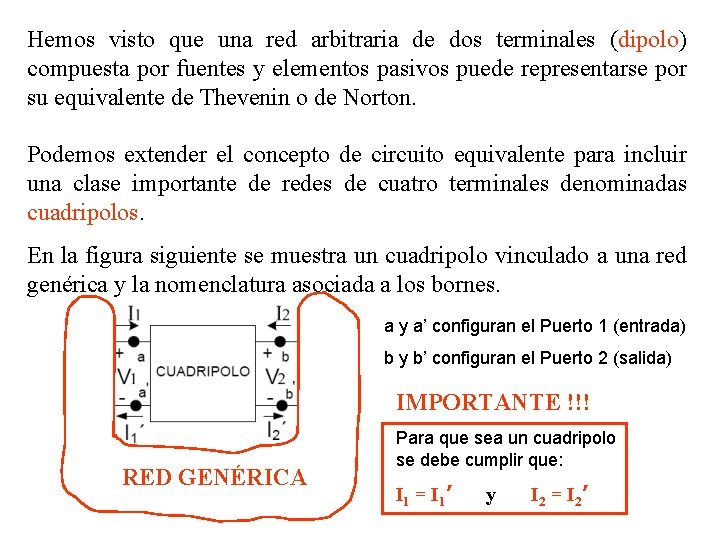
Hemos visto que una red arbitraria de dos terminales (dipolo) compuesta por fuentes y elementos pasivos puede representarse por su equivalente de Thevenin o de Norton. Podemos extender el concepto de circuito equivalente para incluir una clase importante de redes de cuatro terminales denominadas cuadripolos. En la figura siguiente se muestra un cuadripolo vinculado a una red genérica y la nomenclatura asociada a los bornes. a y a’ configuran el Puerto 1 (entrada) b y b’ configuran el Puerto 2 (salida) IMPORTANTE !!! RED GENÉRICA Para que sea un cuadripolo se debe cumplir que: I 1 = I 1 ’ y I 2 = I 2 ’

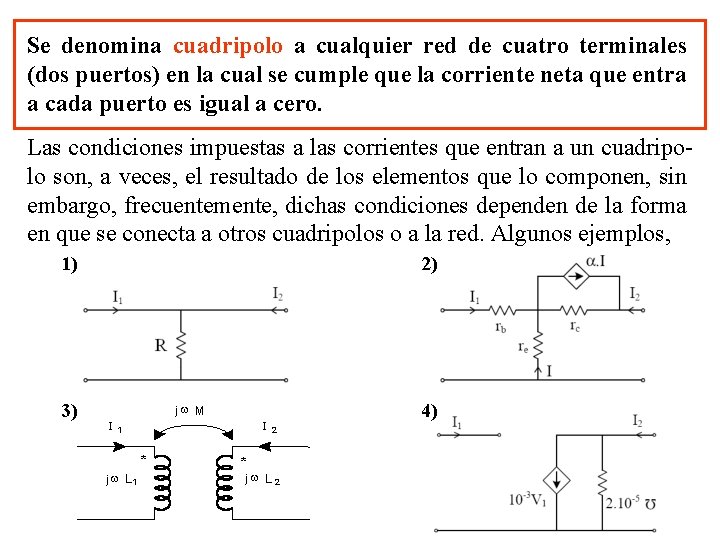
Se denomina cuadripolo a cualquier red de cuatro terminales (dos puertos) en la cual se cumple que la corriente neta que entra a cada puerto es igual a cero. Las condiciones impuestas a las corrientes que entran a un cuadripolo son, a veces, el resultado de los elementos que lo componen, sin embargo, frecuentemente, dichas condiciones dependen de la forma en que se conecta a otros cuadripolos o a la red. Algunos ejemplos, 1) 3) 2) 4) jw M I I 1 j w L 1 * * 2 jw L 2

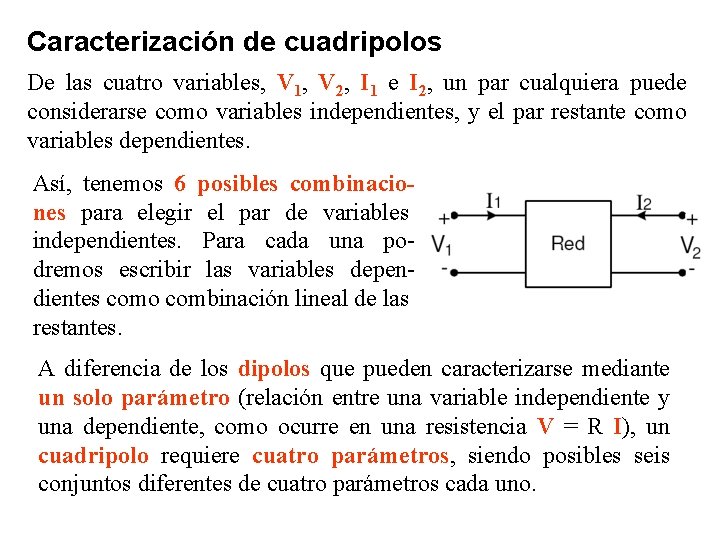
Caracterización de cuadripolos De las cuatro variables, V 1, V 2, I 1 e I 2, un par cualquiera puede considerarse como variables independientes, y el par restante como variables dependientes. Así, tenemos 6 posibles combinaciones para elegir el par de variables independientes. Para cada una podremos escribir las variables dependientes como combinación lineal de las restantes. A diferencia de los dipolos que pueden caracterizarse mediante un solo parámetro (relación entre una variable independiente y una dependiente, como ocurre en una resistencia V = R I), un cuadripolo requiere cuatro parámetros, siendo posibles seis conjuntos diferentes de cuatro parámetros cada uno.

Parámetros admitancia en cortocircuito ( Y ) Tomando V 1 y V 2 como variables independientes, e I 1 e I 2 como dependientes, podemos escribir: V 1 V 2 Donde, los parámetros quedarán definidos según: Para el cálculo práctico de y 11 y y 21 podemos cortocircuitar los bornes 2 -2’, conectar una fuente V 1=1 V, medir I 1 e I 2 y calcular las relaciones respectivas. Un los otrosde de y 12 y y 22 • Enplanteo caso de similar trabajar vale en CCpara hablaremos conductancias. + parámetros 1 V por ej. V =1 V cortocircuitando los bornes 1 -1’ y forzando • y , y son las admitancias de entrada vistas desde 21 -1' o 2 -2‘. 11 22 • y 12 , y 21 son las admitancias de transferencia.

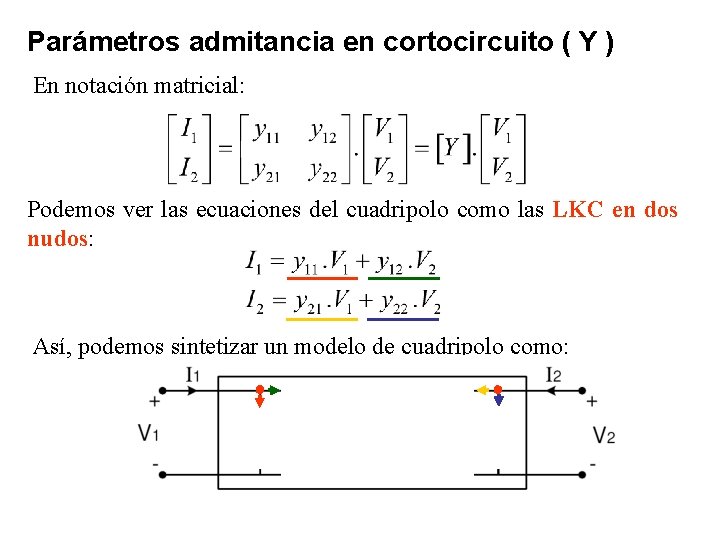
Parámetros admitancia en cortocircuito ( Y ) En notación matricial: Podemos ver las ecuaciones del cuadripolo como las LKC en dos nudos: Así, podemos sintetizar un modelo de cuadripolo como:

Parámetros impedancia en circuito abierto ( Z ) Tomando I 1 e I 2 como variables independientes, y V 1 y V 2 como dependientes, tenemos: I 1 I 2 Donde, los parámetros quedarán definidos según: Para calcular los parámetros z 11 y z 21 podemos dejar los bornes 2 -2' abiertos, conectar una fuente I 1=1 A , medir V 1 y V 2 y calcular las relaciones correspondientes. + + Un para los otros parámetros de z y • Enplanteo caso de similar trabajar vale en CC hablaremos de resistencias. 12 V 2 z 22 1 A V 1 dejando bornes 1 -1’ forzando por- desde ej. I 2 =1 A • z , z abiertos son las los impedancias de yentrada vistas 1 -1' o 2 -2‘. 11 22 • z 12 , z 21 son las impedancias de transferencia.

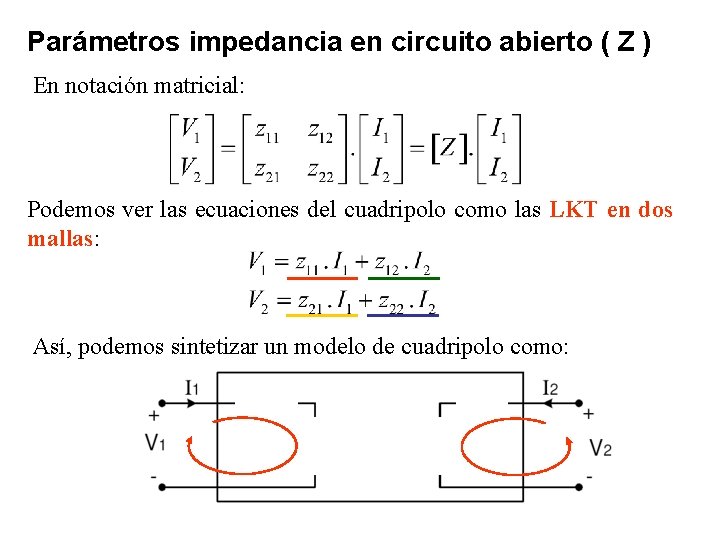
Parámetros impedancia en circuito abierto ( Z ) En notación matricial: Podemos ver las ecuaciones del cuadripolo como las LKT en dos mallas: Así, podemos sintetizar un modelo de cuadripolo como:

Parámetros híbridos ( H ) Tomando I 1 y V 2 como variables independientes, y V 1 e I 2 como dependientes, tenemos: I 1 V 2 Donde, los parámetros quedarán definidos según: Para calcular h 11 y h 21 habrá que cortocircuitar los bornes 2 -2' y realizar los cálculos correspondientes, mientras que para calcular h 12 y h 22 deberemos dejar los bornes 1 -1' abiertos. • h 11 impedancia de entrada del puerto 1 con el puerto 2 cortocircuitado • h 12 inversa de la ganancia en tensión en circuito abierto. • h 21 ganancia de corriente en cortocircuito. • h 22 admitancia de entrada del puerto 2 con el puerto 1 en circ. abierto.

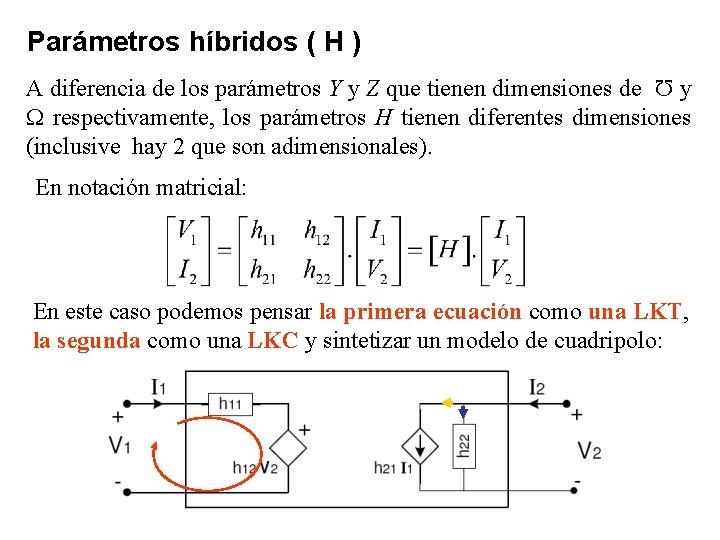
Parámetros híbridos ( H ) A diferencia de los parámetros Y y Z que tienen dimensiones de y respectivamente, los parámetros H tienen diferentes dimensiones (inclusive hay 2 que son adimensionales). En notación matricial: En este caso podemos pensar la primera ecuación como una LKT, la segunda como una LKC y sintetizar un modelo de cuadripolo:

Parámetros híbridos ( H’ ) También podríamos haber definido una segunda matriz híbrida, tomando como variables independientes la tensión V 1 y la corriente I 2. A esto parámetros se los conoce como parámetros H’. V 1 I 2 En notación matricial: Se ve claramente que H' = H-1 si H es no singular. Ejercicio: Plantear un modelo circuital genérico de un cuadripolo representado a partir de parámetro H’.

Parámetros de transferencia o fundamentales ( T ) Tomando I 2 e V 2 como variables independientes, y V 1 e I 1 como dependientes, tenemos: V 2 I 2 Donde, los parámetros quedarán definidos según: En este caso los ensayos para poder determinar los parámetros se realizan cortocircuitando (para los parámetros B y D) o dejando abierto (para los parámetros A y C) el puerto 2. • A : ganancia de tensión c/puerto 2 en circuito abierto. • B : impedancia de transferencia en cortocircuito. • C : admitancia de transferencia en circuito abierto. • D : opuesto de la ganancia de corriente c/puerto 2 en cortocircuito

Parámetros de transferencia o fundamentales ( T ) En notación matricial: En este caso, no se puede dibujar un circuito equivalente como se hizo en los casos anteriores, dado que ambas ecuaciones corresponden a las variables tensión y corriente en el mismo puerto. Estos parámetros son muy convenientes para analizar redes conectadas en cascada, como se vera más adelante.

Parámetros de transferencia inversa ( T’ ) Si hubiéramos tomando como variables independientes la tensión V 1 y la corriente I 1 podríamos también haber definido una segunda matriz de transferencia, tal que: V 1 I 1 En notación matricial: Vemos que, la matriz de transferencia directa T expresa tensión y corriente en el puerto 1 en función de la tensión y corriente en el puerto 2, y la matriz de transferencia inversa T ' expresa la tensión y corriente en el puerto 2 en función de la tensión y corriente en el puerto 1, resulta que ambas matrices son inversas, es decir [T'] = [T]-1.

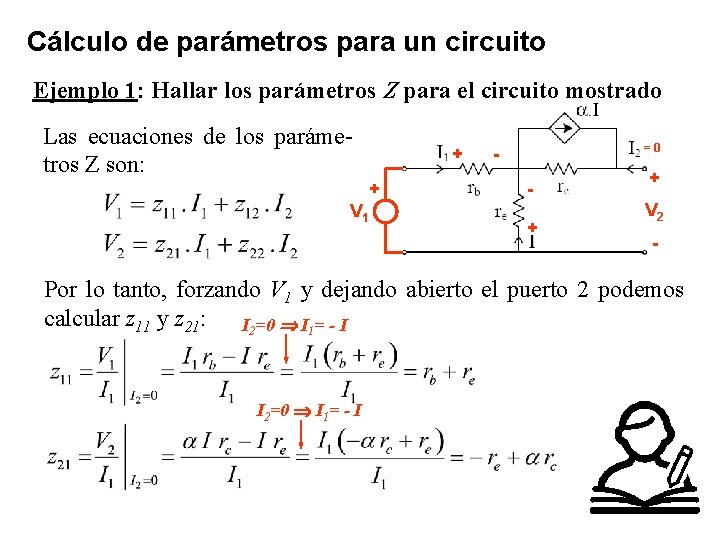
Cálculo de parámetros para un circuito Ejemplo 1: Hallar los parámetros Z para el circuito mostrado Las ecuaciones de los parámetros Z son: + + V 1 =0 + + V 2 - Por lo tanto, forzando V 1 y dejando abierto el puerto 2 podemos calcular z 11 y z 21: I 2=0 I 1= - I

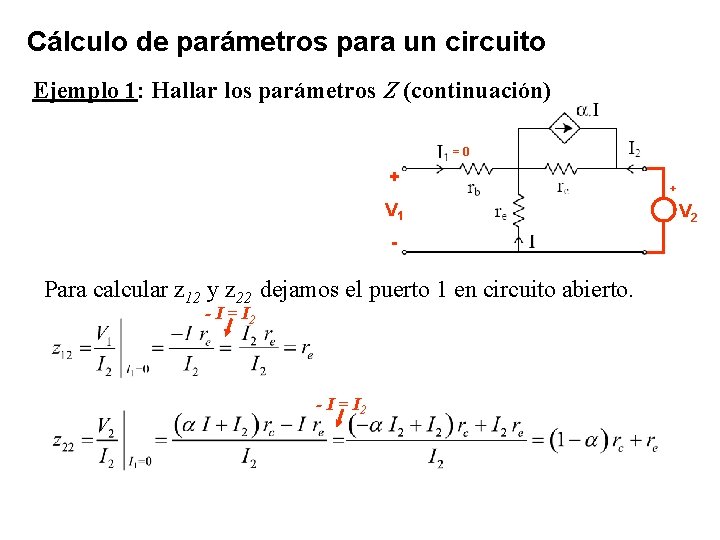
Cálculo de parámetros para un circuito Ejemplo 1: Hallar los parámetros Z (continuación) =0 + V 1 - Para calcular z 12 y z 22 dejamos el puerto 1 en circuito abierto. - I = I 2 + V 2

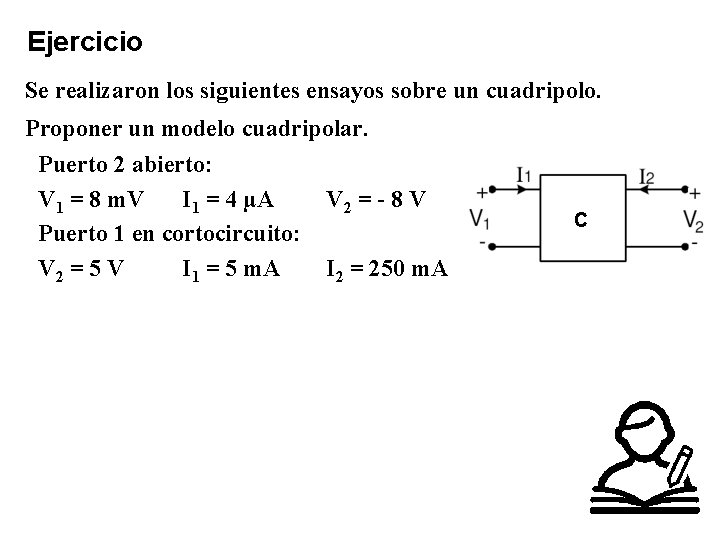
Ejercicio Se realizaron los siguientes ensayos sobre un cuadripolo. Proponer un modelo cuadripolar. Puerto 2 abierto: V 1 = 8 m. V I 1 = 4 µA Puerto 1 en cortocircuito: V 2 = 5 V I 1 = 5 m. A V 2 = - 8 V I 2 = 250 m. A C

Cálculo de parámetros a partir de ensayos Ejemplo 2: Se realizaron los siguientes ensayos sobre un cuadripolo. Proponer un modelo cuadripolar. Puerto 2 abierto ( I 2 = 0 A ): V 1 = 8 m. V I 1 = 4 µA V 2 = - 8 V Puerto 2 en cortocircuito ( V 2 = 0 A ): V 1 = 5 V I 1 = 5 m. A I 2 = 250 m. A C Como las variables que se anulan en los ensayos son siempre las variables independientes, V 1 e I 1 se escribirán en función de las mismas tal que: luego

Relaciones entre los distintos tipos de parámetros Sucederá a veces que teniendo expresado un cuadripolo a través de un determinado juego de parámetros, nos interesará conocer otra representación. Para ello, operando algebraicamente, podremos obtener cualquiera de los otros juegos de parámetros. Ejemplo 3: Hallar los parámetros H en función de los Z Conocidos queremos calcular Despejando I 2 de la segunda ecuación: Reemplazando en la primer ecuación y reagrupando tenemos:

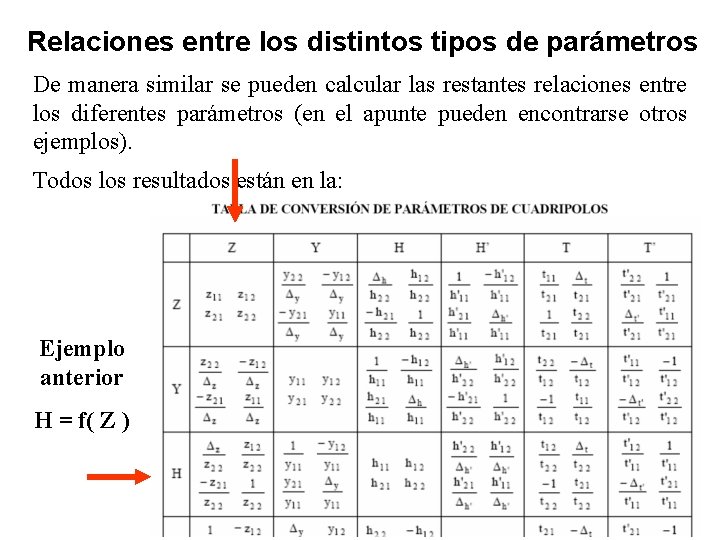
Relaciones entre los distintos tipos de parámetros De manera similar se pueden calcular las restantes relaciones entre los diferentes parámetros (en el apunte pueden encontrarse otros ejemplos). Todos los resultados están en la: Ejemplo anterior H = f( Z )

Cuadripolos recíprocos Se dice que un cuadripolo es recíproco si su matriz de admitancia en cortocircuito y su matriz impedancia en circuito abierto son simétricas (es decir, si aij = aji para todo j). En otras palabras, si es simétrica respecto a la diagonal principal. Para que se verifique esta condición el cuadripolo solo debe contener elementos pasivos (pero no fuentes controladas). Analizando las ecuaciones del modelo en parámetros Z: Vemos entonces que podemos caracterizarlo solo con tres parámetros. Si suponemos que las ecuaciones anteriores corresponden al método de bucles, vemos que existe un vínculo galvánico entre las mallas de entrada y de salida debido justamente al elemento z 12.

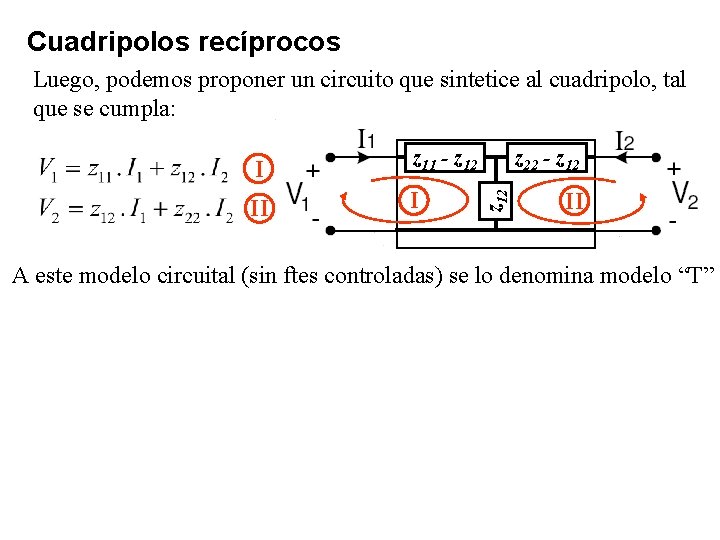
Cuadripolos recíprocos Luego, podemos proponer un circuito que sintetice al cuadripolo, tal que se cumpla: z 11 - z 12 II I z 22 - z 12 C C z 12 I II y 12 C y 22 - y 12 y 11 - y 12 A este modelo circuital (sin ftes controladas) se lo denomina modelo “T” Análogamente, veamos que ocurre si consideramos las ecuaciones de un cuadripolo a partir de sus parametros Y, pero pensando en ecuaciones de nudos: A este modelo circuital se lo denomina modelo “ ” (o triángulo).

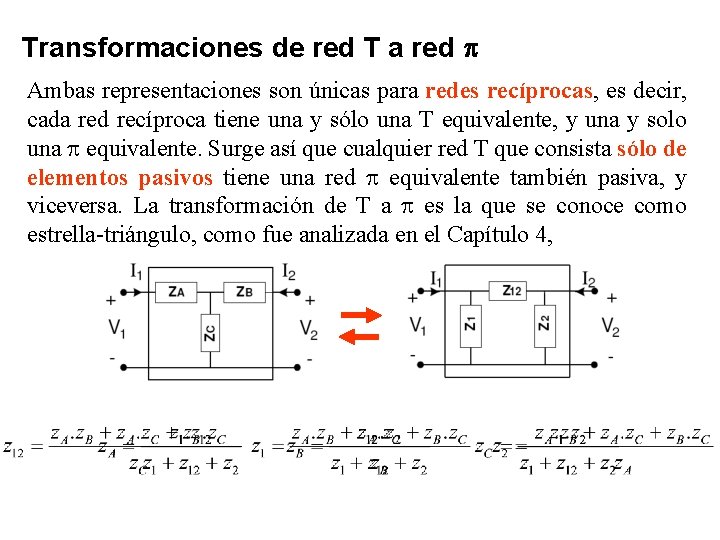
Transformaciones de red T a red Ambas representaciones son únicas para redes recíprocas, es decir, cada red recíproca tiene una y sólo una T equivalente, y una y solo una equivalente. Surge así que cualquier red T que consista sólo de elementos pasivos tiene una red equivalente también pasiva, y viceversa. La transformación de T a es la que se conoce como estrella-triángulo, como fue analizada en el Capítulo 4,

Interconexión de cuadripolos A continuación, analizaremos las distintas posibilidades de interconectar 2 cuadripolos según como se conecten entre si los puertos de entrada y de salida de cada cuadripolo. Así, tendremos 5 (cinco) opciones: serie-serie, paralelo-paralelo, cascada y las conexiones mixtas: serie-paralelo y paralelo-serie. Es interesante analizar para cada interconexión cuál es el juego de parámetros más conveniente para hallar un cuadripolo equivalente de la interconexión.

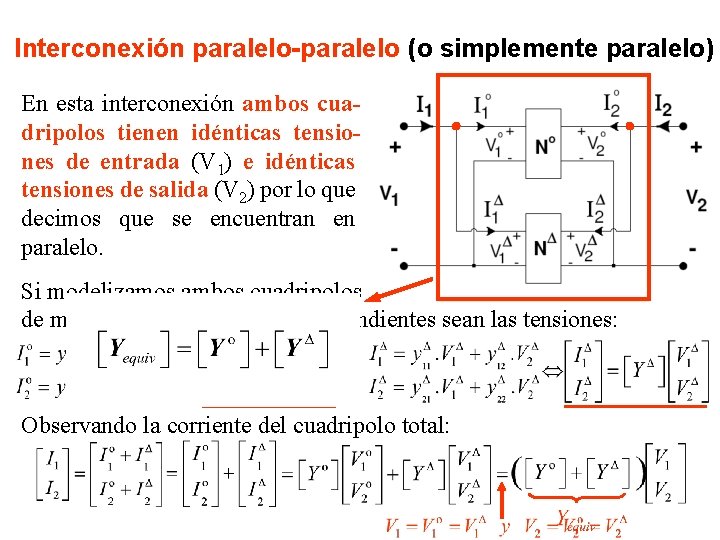
Interconexión paralelo-paralelo (o simplemente paralelo) En esta interconexión ambos cuadripolos tienen idénticas tensiones de entrada (V 1) e idénticas tensiones de salida (V 2) por lo que decimos que se encuentran en paralelo. Si modelizamos ambos cuadripolos de manera que las variables independientes sean las tensiones: Observando la corriente del cuadripolo total:

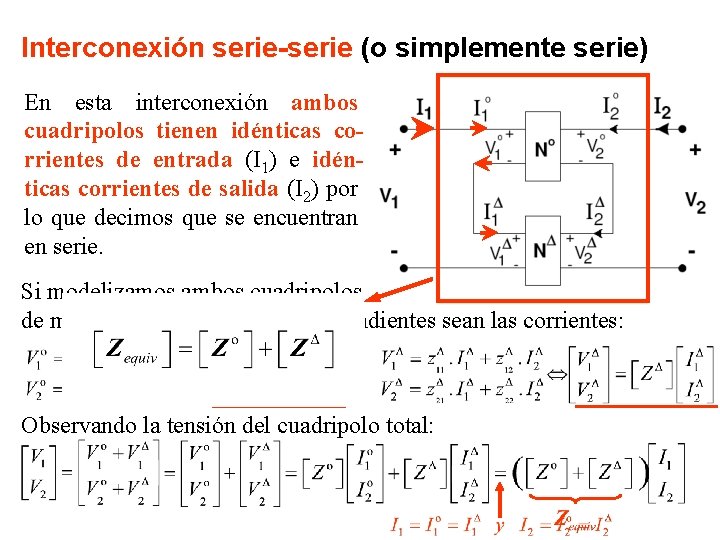
Interconexión serie-serie (o simplemente serie) En esta interconexión ambos cuadripolos tienen idénticas corrientes de entrada (I 1) e idénticas corrientes de salida (I 2) por lo que decimos que se encuentran en serie. Si modelizamos ambos cuadripolos de manera que las variables independientes sean las corrientes: Observando la tensión del cuadripolo total:

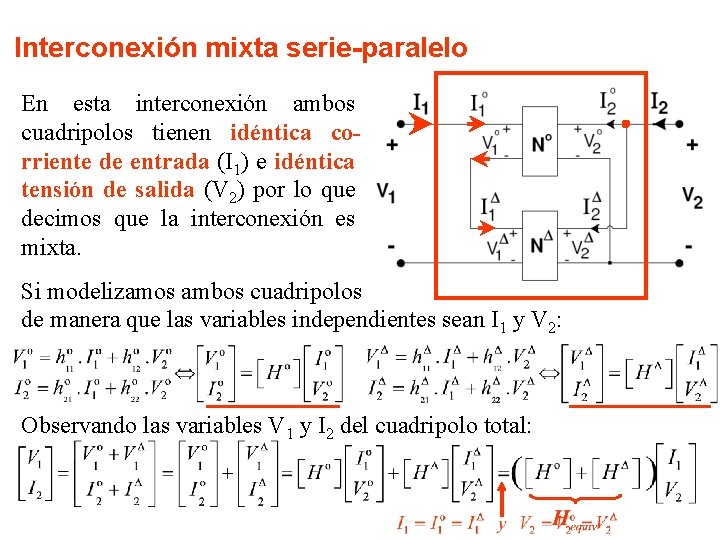
Interconexión mixta serie-paralelo En esta interconexión ambos cuadripolos tienen idéntica corriente de entrada (I 1) e idéntica tensión de salida (V 2) por lo que decimos que la interconexión es mixta. Si modelizamos ambos cuadripolos de manera que las variables independientes sean I 1 y V 2: Observando las variables V 1 y I 2 del cuadripolo total:

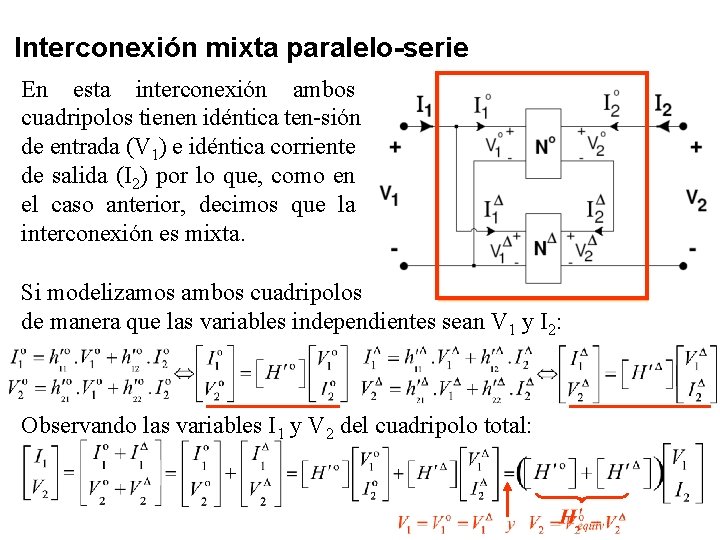
Interconexión mixta paralelo-serie En esta interconexión ambos cuadripolos tienen idéntica ten-sión de entrada (V 1) e idéntica corriente de salida (I 2) por lo que, como en el caso anterior, decimos que la interconexión es mixta. Si modelizamos ambos cuadripolos de manera que las variables independientes sean V 1 y I 2: Observando las variables I 1 y V 2 del cuadripolo total:

Interconexión de cuadripolos Resumiendo, de acuerdo a como estén conectados los puertos de entrada y los puertos de salida de los cuadripolos será conveniente utilizar un juego de parámetros determinados para hallar una representación equivalente resultante de la interconexión. PARALELO SERIE Puertos de salida Puertos de entrada SERIE PARALELO

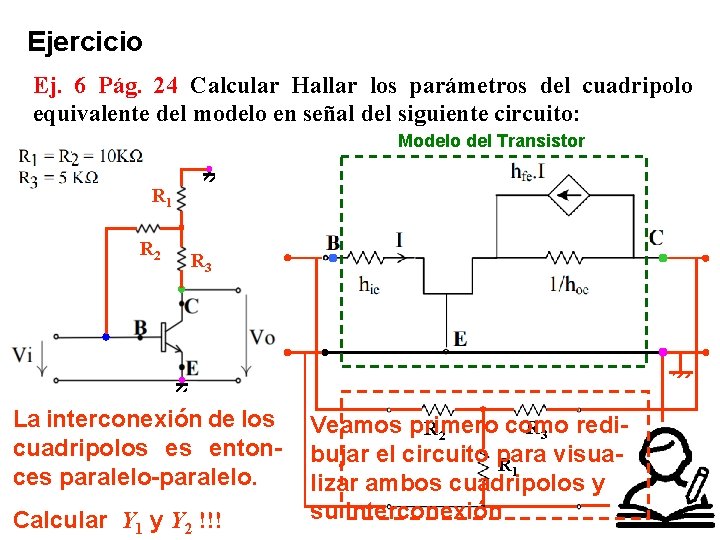
Ejercicio Ej. 6 Pág. 24 Calcular Hallar los parámetros del cuadripolo equivalente del modelo en señal del siguiente circuito: Modelo del Transistor R 1 R 2 R 3 La interconexión de los cuadripolos es entonces paralelo-paralelo. Calcular Y 1 y Y 2 !!! Veamos primero como R 3 redi. R 2 bujar el circuito para visua. R 1 lizar ambos cuadripolos y su interconexión

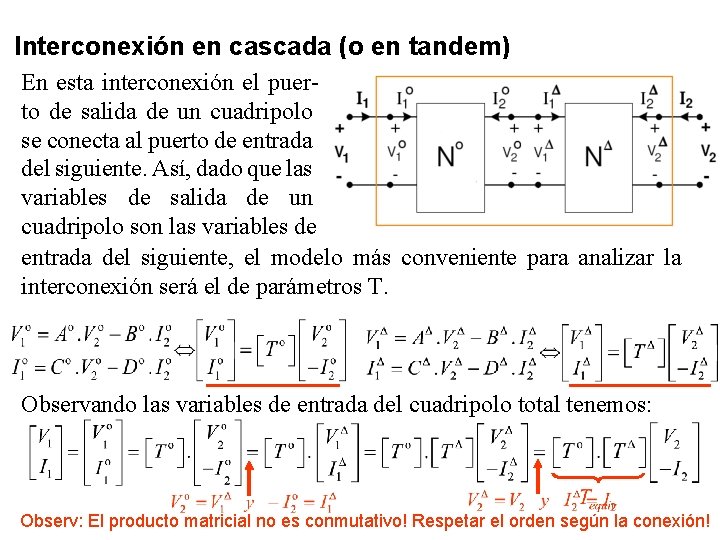
Interconexión en cascada (o en tandem) En esta interconexión el puerto de salida de un cuadripolo se conecta al puerto de entrada del siguiente. Así, dado que las variables de salida de un cuadripolo son las variables de entrada del siguiente, el modelo más conveniente para analizar la interconexión será el de parámetros T. Observando las variables de entrada del cuadripolo total tenemos: Observ: El producto matricial no es conmutativo! Respetar el orden según la conexión!

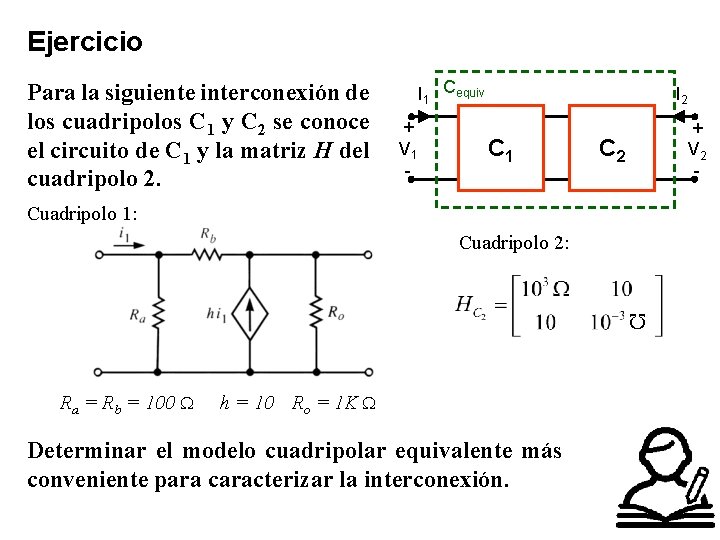
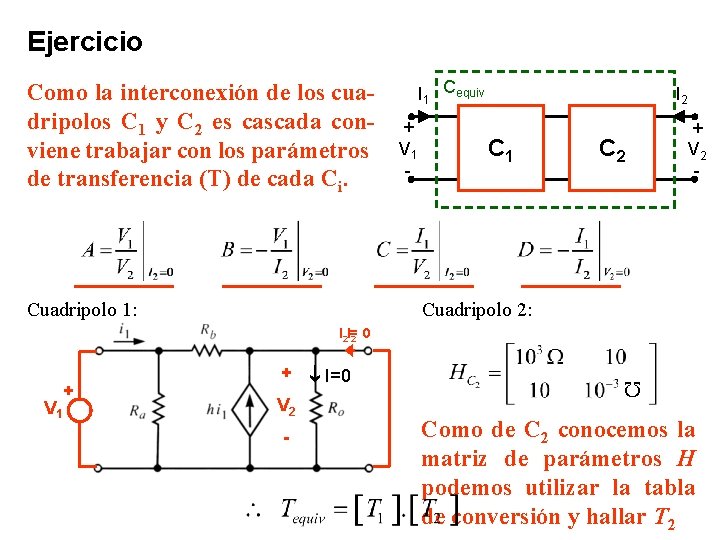
Ejercicio Para la siguiente interconexión de los cuadripolos C 1 y C 2 se conoce el circuito de C 1 y la matriz H del cuadripolo 2. I 1 Cequiv + V 1 - I 2 C 1 + V 2 - C 2 Cuadripolo 1: Cuadripolo 2: Ra = Rb = 100 h = 10 Ro = 1 K Determinar el modelo cuadripolar equivalente más conveniente para caracterizar la interconexión.

Ejercicio Como la interconexión de los cuadripolos C 1 y C 2 es cascada conviene trabajar con los parámetros de transferencia (T) de cada Ci. Cuadripolo 1: I 1 Cequiv + V 1 - I 2 C 1 C 2 + V 2 - Cuadripolo 2: I 2 I= 2 0 V 2 - V 1 + + I=0 Como de C 2 conocemos la matriz de parámetros H podemos utilizar la tabla de conversión y hallar T 2

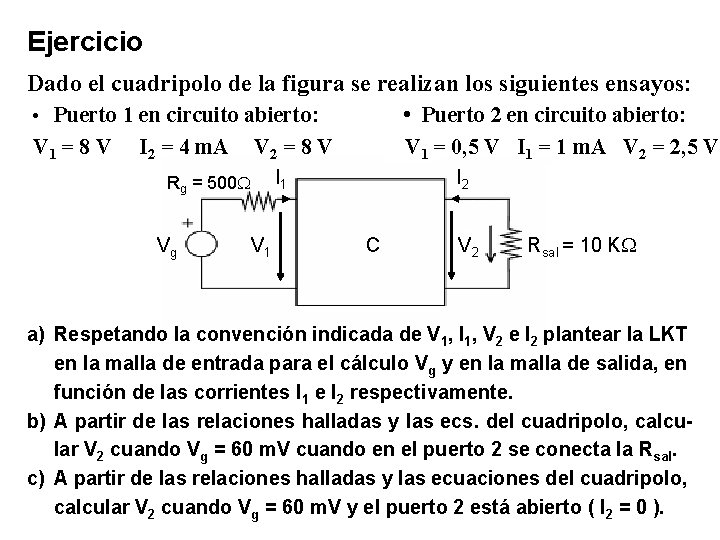
Ejercicio Dado el cuadripolo de la figura se realizan los siguientes ensayos: • Puerto 1 en circuito abierto: V 1 = 8 V I 2 = 4 m. A V 2 = 8 V Rg = 500 Vg I 1 • Puerto 2 en circuito abierto: V 1 = 0, 5 V I 1 = 1 m. A V 2 = 2, 5 V I 2 V 1 C V 2 Rsal = 10 K a) Respetando la convención indicada de V 1, I 1, V 2 e I 2 plantear la LKT en la malla de entrada para el cálculo Vg y en la malla de salida, en función de las corrientes I 1 e I 2 respectivamente. b) A partir de las relaciones halladas y las ecs. del cuadripolo, calcular V 2 cuando Vg = 60 m. V cuando en el puerto 2 se conecta la Rsal. c) A partir de las relaciones halladas y las ecuaciones del cuadripolo, calcular V 2 cuando Vg = 60 m. V y el puerto 2 está abierto ( I 2 = 0 ).

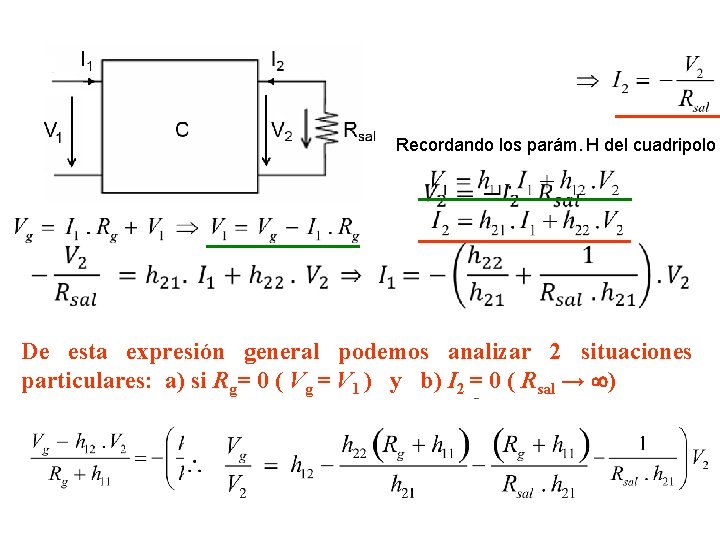
Recordando los parám. H del cuadripolo De esta expresión general podemos analizar 2 situaciones particulares: a) si Rg= 0 ( Vg = V 1 ) y b) I 2 = 0 ( Rsal → )

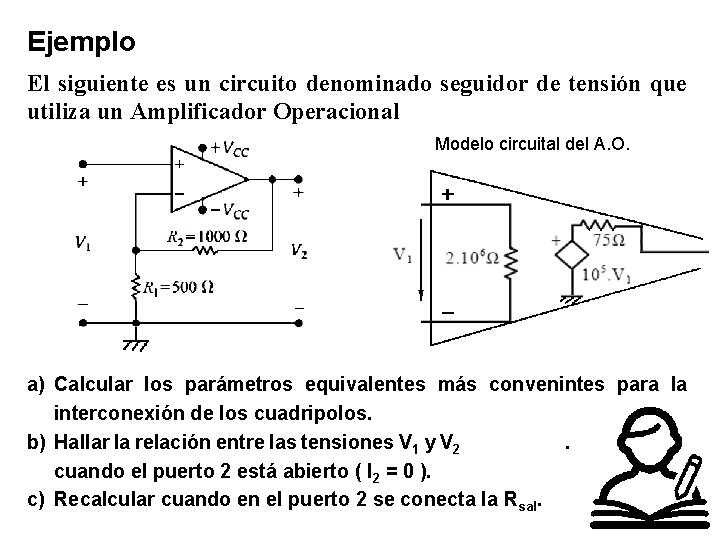
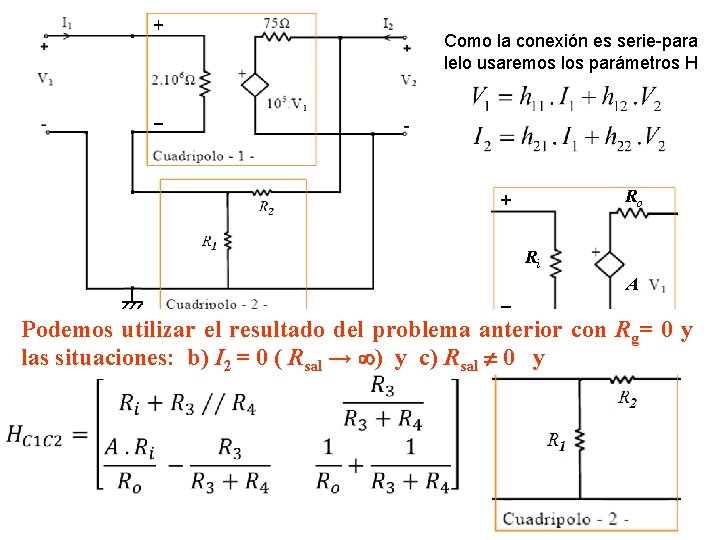
Ejemplo El siguiente es un circuito denominado seguidor de tensión que utiliza un Amplificador Operacional Modelo circuital del A. O. a) Calcular los parámetros equivalentes más convenintes para la interconexión de los cuadripolos. b) Hallar la relación entre las tensiones V 1 y V 2. cuando el puerto 2 está abierto ( I 2 = 0 ). c) Recalcular cuando en el puerto 2 se conecta la Rsal.

Como la conexión es serie-para lelo usaremos los parámetros H Ro Ri A Podemos utilizar el resultado del problema anterior con Rg= 0 y las situaciones: b) I 2 = 0 ( Rsal → ) y c) Rsal 0 y

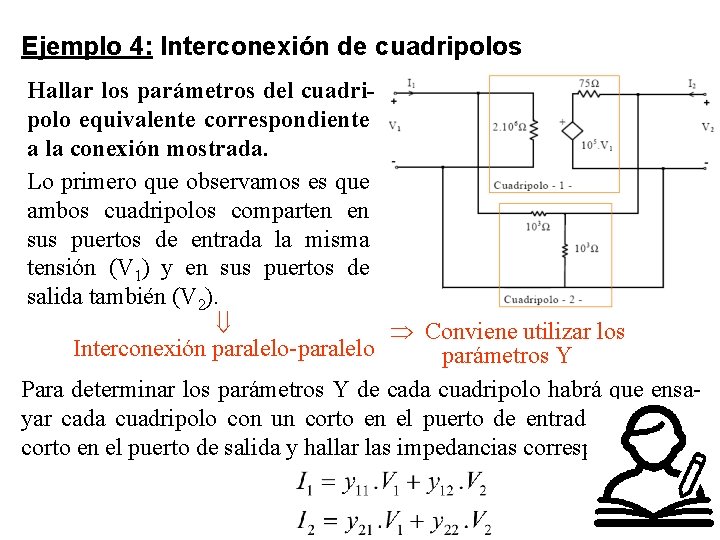
Ejemplo 4: Interconexión de cuadripolos Hallar los parámetros del cuadripolo equivalente correspondiente a la conexión mostrada. Lo primero que observamos es que ambos cuadripolos comparten en sus puertos de entrada la misma tensión (V 1) y en sus puertos de salida también (V 2). Conviene utilizar los Interconexión paralelo-paralelo parámetros Y Para determinar los parámetros Y de cada cuadripolo habrá que ensayar cada cuadripolo con un corto en el puerto de entrada y con un corto en el puerto de salida y hallar las impedancias correspondientes.

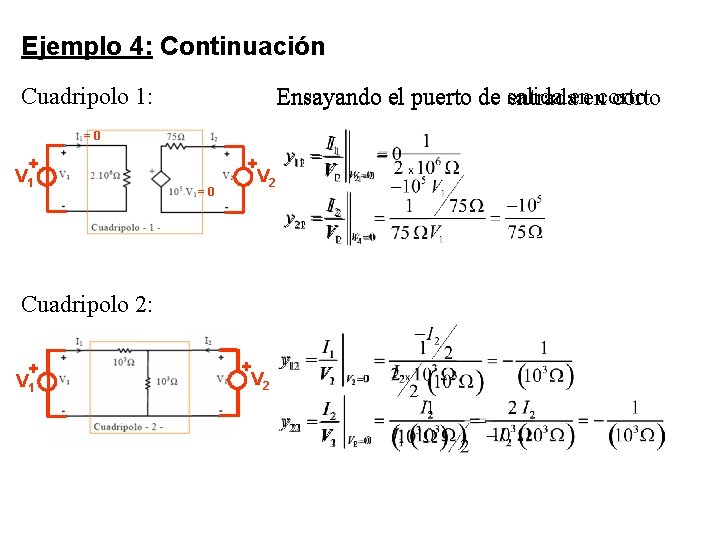
Ejemplo 4: Continuación Cuadripolo 1: salida enencorto Ensayando el puerto de entrada corto =0 + V 1 =0 + V 2 Cuadripolo 2: + V 1 + V 2

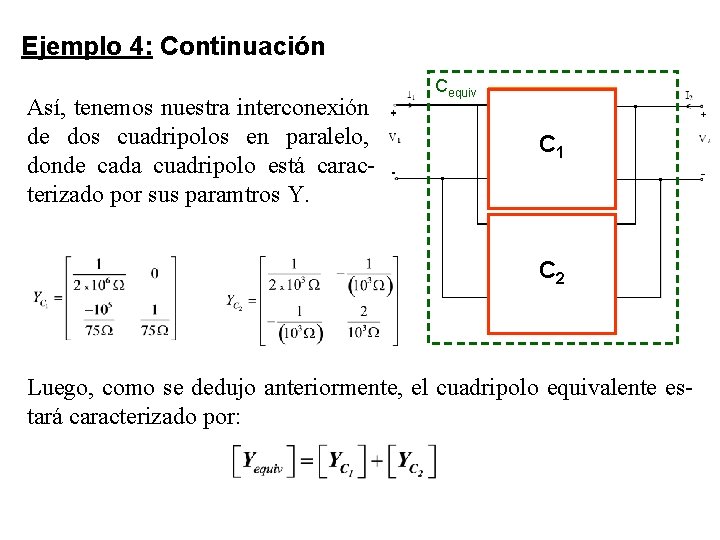
Ejemplo 4: Continuación Así, tenemos nuestra interconexión de dos cuadripolos en paralelo, donde cada cuadripolo está caracterizado por sus paramtros Y. Cequiv C 1 C 2 Luego, como se dedujo anteriormente, el cuadripolo equivalente estará caracterizado por:

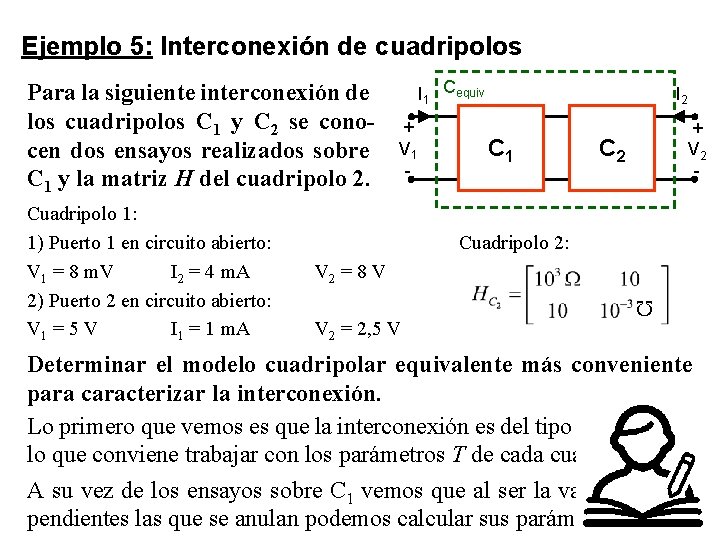
Ejemplo 5: Interconexión de cuadripolos Para la siguiente interconexión de los cuadripolos C 1 y C 2 se conocen dos ensayos realizados sobre C 1 y la matriz H del cuadripolo 2. + V 1 - I 2 C 1 + V 2 - C 2 Cuadripolo 2: V 2 = 8 V V 2 = 2, 5 V Cuadripolo 1: 1) Puerto 1 en circuito abierto: V 1 = 8 m. V I 2 = 4 m. A 2) Puerto 2 en circuito abierto: V 1 = 5 V I 1 = 1 m. A I 1 Cequiv Determinar el modelo cuadripolar equivalente más conveniente para caracterizar la interconexión. Lo primero que vemos es que la interconexión es del tipo cascada, por lo que conviene trabajar con los parámetros T de cada cuadripolo. A su vez de los ensayos sobre C 1 vemos que al ser la variables independientes las que se anulan podemos calcular sus parámetros Z.

Ejemplo 5: Continuación Cuadripolo 1: ZC 1 Tabla TC 1 Cuadripolo 2: HC 2 Tabla TC 2 Como ya vimos anteriormente para la interconexión en cascada, la matriz de parametros equivalente Tequiv se obtiene a partir de la multiplicación matricial de TC 1 por TC 2.

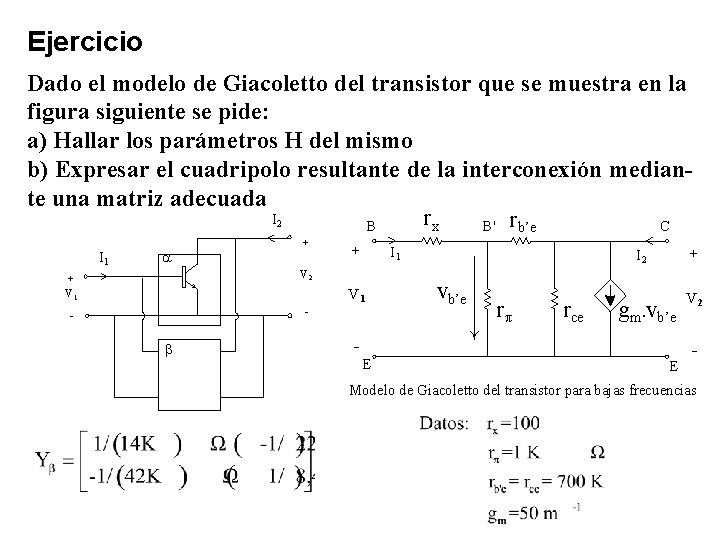
Ejercicio Dado el modelo de Giacoletto del transistor que se muestra en la figura siguiente se pide: a) Hallar los parámetros H del mismo b) Expresar el cuadripolo resultante de la interconexión mediante una matriz adecuada I 2 I 1 a + + V 1 _ _ b B' rb’e C I 1 V 2 + V 1 rx B + I 2 vb’e r rce gm. vb’e _ V 2 _ E E Modelo de Giacoletto del transistor para bajas frecuencias