Base Conversions Convert 12310 to Base 10 gotta

Base Conversions Convert 123|10 to Base 10 (gotta start someplace) 1 2 3 |10 | | | `----`------- = ? |10 3 x 100 = 3 x 1 = 3 2 x 101 = 2 x 10 = 20 1 x 102 = 1 x 100 = 100 123 Therefore, 123|10 = 123|10

Base Conversions Convert 123|8 to Base 10 1 2 3 |8 = ? |10 | | | `--- 3 x 80 = 3 x | `----- 2 x 81 = 2 x `------- 1 x 82 = 1 x Therefore, 123|8 = 83|10 1 = 8 = 64 = 3 16 64 83

Base Conversions Convert 2 BAD|16 to Base 10 2 B A D |16 | | | | `--| | `------`----- = ? |10 D A B 2 x x 160 161 162 163 = 13 x 1 = 10 x 16 = 11 x 256 = 2 x 4096 Therefore, 2 BAD|16 = 11181|10 = = 13 160 2816 8192 11181

Base Conversions Convert 20 DD|16 to Base 10 ? ?

Base Conversions Convert 20 DD|16 to Base 10 2 0 D D |16 | | | | `--| | `------`----- = ? |10 D D 0 2 x x 160 161 162 163 = 13 x 16 = 0 x 256 = 2 x 4096 Therefore, 20 DD|16 = 8413|10 = = 13 208 0 8192 8413

Base Conversions Convert FACE|16 to Base 10 ? ?

Base Conversions Convert FACE|16 to Base 10 F A C E |16 | | | | `--| | `------`----- = ? |10 E C A F x x 160 161 162 163 = = 14 12 10 15 x 16 x 256 x 4096 Therefore, FACE|16 = 64206|10 = 14 = 192 = 2560 = 61440 64206

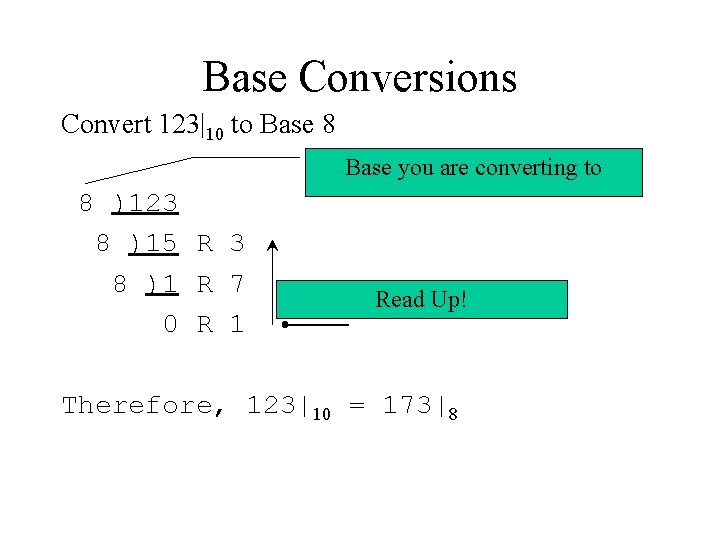
Base Conversions Convert 123|10 to Base 8 Base you are converting to 8 )123 8 )15 R 3 8 )1 R 7 0 R 1 Read Up! Therefore, 123|10 = 173|8

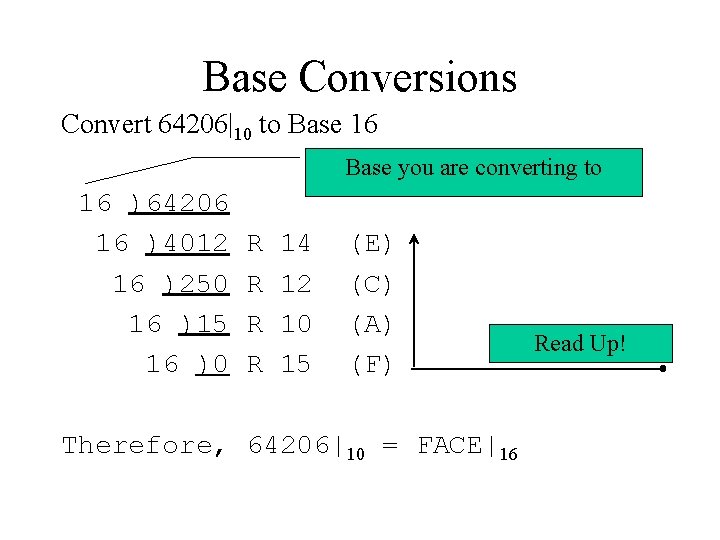
Base Conversions Convert 64206|10 to Base 16 Base you are converting to 16 )64206 16 )4012 16 )250 16 )15 16 )0 R R 14 12 10 15 (E) (C) (A) (F) Therefore, 64206|10 = FACE|16 Read Up!

Base Conversions 123|7 = ? |9 (Can’t do directly) Step 1: 123|7=? |10 1 2 3 | | | `-3 x 70= 3 | `--2 x 71=14 `-----1 x 72=49 66 123|7=66|10 Step 2: 66|10=? |9 9 )66 9 ) 7 R 3 0 R 7 66|10=73|9 123|7=73|9

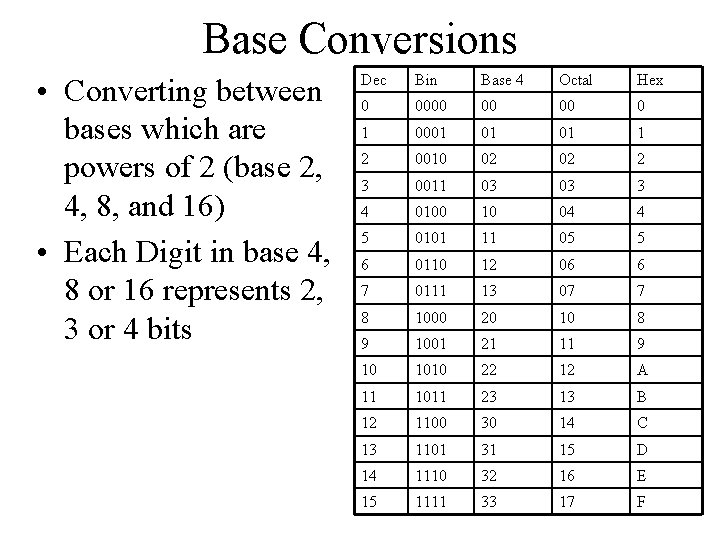
Base Conversions • Converting between bases which are powers of 2 (base 2, 4, 8, and 16) • Each Digit in base 4, 8 or 16 represents 2, 3 or 4 bits Dec Bin Base 4 Octal Hex 0 0000 00 00 0 1 0001 01 01 1 2 0010 02 02 2 3 0011 03 03 3 4 0100 10 04 4 5 0101 11 05 5 6 0110 12 06 6 7 0111 13 07 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 12 1100 30 14 C 13 1101 31 15 D 14 1110 32 16 E 15 1111 33 17 F

Base Conversions Dec Bin Bs 4 Oct Hex 0 0000 00 00 0 1 0001 01 01 1 2 0010 02 02 2 3 0011 03 03 3 4 0100 10 04 4 5 0101 11 05 5 6 0110 12 06 6 7 0111 13 07 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 10101110001101|2=25615|8 12 1100 30 14 C 13 1101 31 15 D NOTE: # is a place holder for zero 14 1110 32 16 E 15 1111 33 17 F 10101110001101|2=? |8 Work from right to left Divide into 3 bit groups #10 101 110 001 101 2 5 6 1 5

Base Conversions Dec Bin Bs 4 Oct Hex 0 0000 00 00 0 1 0001 01 01 1 2 0010 02 02 2 3 0011 03 03 3 4 0100 10 04 4 5 0101 11 05 5 6 0110 12 06 6 7 0111 13 07 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 10101110001101|2=2 B 8 D|16 12 1100 30 14 C 13 1101 31 15 D NOTE: # is a place holder for zero 14 1110 32 16 E 15 1111 33 17 F 10101110001101|2=? |16 Work from right to left Divide into 4 bit groups ##10 1011 1000 1101 2 B 8 D

Base Conversions 1357|8=? |2 1 3 5 7 001 011 101 111 1357|8=00101111|2 Note: one need not write the leading zeros Dec Bin Bs 4 Oct Hex 0 0000 00 00 0 1 0001 01 01 1 2 0010 02 02 2 3 0011 03 03 3 4 0100 10 04 4 5 0101 11 05 5 6 0110 12 06 6 7 0111 13 07 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 12 1100 30 14 C 13 1101 31 15 D 14 1110 32 16 E 15 1111 33 17 F

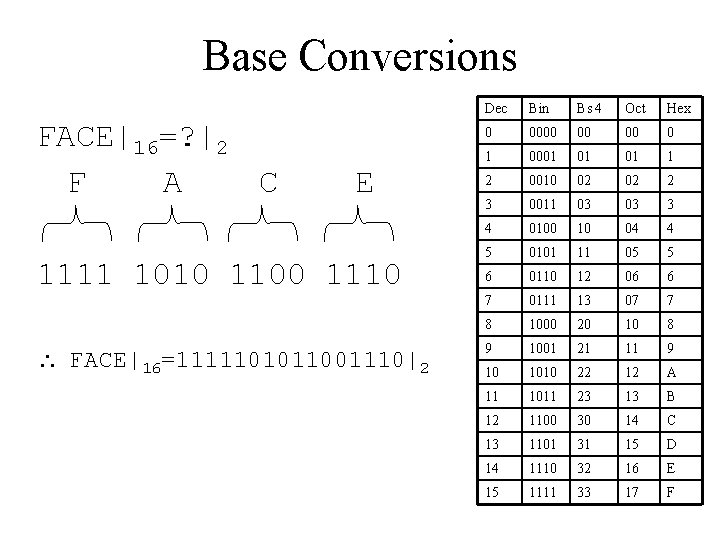
Base Conversions FACE|16=? |2 F A C E 1111 1010 1100 1110 FACE|16=1111101011001110|2 Dec Bin Bs 4 Oct Hex 0 0000 00 00 0 1 0001 01 01 1 2 0010 02 02 2 3 0011 03 03 3 4 0100 10 04 4 5 0101 11 05 5 6 0110 12 06 6 7 0111 13 07 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 12 1100 30 14 C 13 1101 31 15 D 14 1110 32 16 E 15 1111 33 17 F

Base Conversions A 1 CE|16=? |8 2 1 C E 10100001110011 10 1 2 0 7 1 6 A 1 CE|16=120716|8 Dec Bin Bs 4 Oct Hex 0 0000 00 00 0 1 0001 01 01 1 2 0010 02 02 2 3 0011 03 03 3 4 0100 10 04 4 5 0101 11 05 5 6 0110 12 06 6 7 0111 13 07 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 12 1100 30 14 C 13 1101 31 15 D 14 1110 32 16 E 15 1111 33 17 F

Terminology • • Bit – a 0 or a 1 Nibble – 4 bits Byte – 8 bits Word – Machine dependent (8086/88 = 16 bits; 386/486/Pent = 32 bits) • Doubleword – Machine dependent (8086/88 = 32 bits; 386/486/Pent = 64 bits)

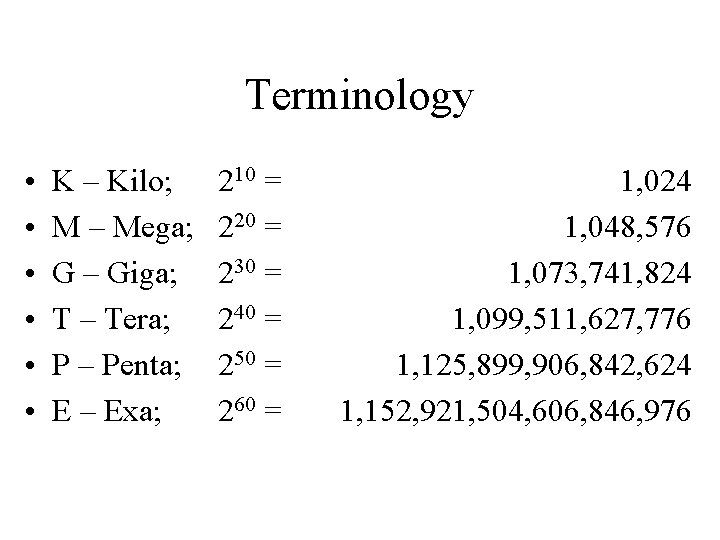
Terminology • • • K – Kilo; M – Mega; G – Giga; T – Tera; P – Penta; E – Exa; 210 = 220 = 230 = 240 = 250 = 260 = 1, 024 1, 048, 576 1, 073, 741, 824 1, 099, 511, 627, 776 1, 125, 899, 906, 842, 624 1, 152, 921, 504, 606, 846, 976

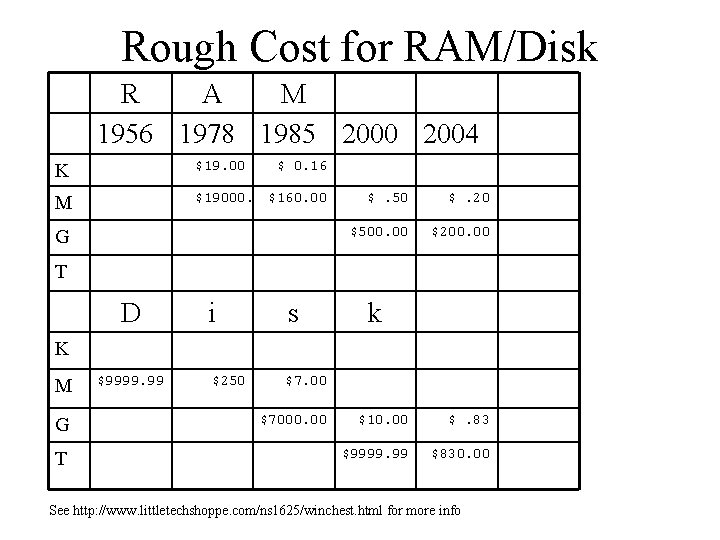
Rough Cost for RAM/Disk R A M 1956 1978 1985 2000 2004 K $19. 00 M $19000. $ 0. 16 $160. 00 G $. 50 $. 20 $500. 00 $200. 00 T D i s $250 $7. 00 k K M G T $9999. 99 $7000. 00 $10. 00 $. 83 $9999. 99 $830. 00 See http: //www. littletechshoppe. com/ns 1625/winchest. html for more info

ASCII-American Standard Code for Information Interchange • • Used to represent characters Seven bit code used to represent character ‘ 0’ through ‘ 9’ are characters IBM used 8 bits in PC and added 128 additional characters (line drawing, Greek) • Problem with ASCII – the A • Unicode addresses this problem

ASCII-points to note • Values 30 -39=Chars ‘ 0’-’ 9’ • ‘a’ = ‘A’ + 32 (Bit 5) • ‘A’ = Ctrl/A+64 (bit 6) • ‘A’ < ‘Z’ < ‘a’ < ‘z’ • If character is represented in a byte, bit 7 is usually 0 • Chars 0 -31 d are not printable, but may influence how other chars are printed.

upper 3 bits 000001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 10000 10001 10010 10011 10100 10101 10110 10111 11000 11001 11010 11011 11100 11101 11110 11111 lower 5 bits 000 001 010 011 100 101 110 111

Binary Addition 0+0=0 0+1=1 1+0=1 1 + 1 = 0 (with carry of 1)

1011011 + 10110 = ? 1 0 1 1 + 1 0 1 1 0 --------1 1 1 0 0 0 1

100111001 + 11011 = ? 1 0 0 1 1 1 0 0 1 + 1 1 0 1 1 ---------

100111001 + 11011 = ? 1 0 0 1 1 1 0 0 1 + 1 1 0 1 1 --------1 0 1 0 0

Logical Operations Two possible values - TRUE represented by non-zero - FALSE represented by zero i. e. 5 is TRUE 5. 32 is TRUE 'T' is TRUE 'F' is TRUE -45 is TRUE 0 is FALSE

Logical Operations AND && FALSE TRUE && && 5 && 0 is 4 && 'F' is 'F' && 'F' is 0 && 'T' is 0 && 0 is FALSE TRUE is is FALSE TRUE FALSE (zero) (non-zero) (zero)

Logical Operations OR | | FALSE TRUE || || FALSE TRUE is is FALSE TRUE 5||0 4 | | 'F' 0 | | 'T' 0||0 is is is TRUE FALSE (non-zero) (zero)

Logical Operations XOR ^^ FALSE TRUE ^^ ^^ FALSE TRUE is is FALSE TRUE FALSE 5 ^^ 0 4 ^^ 'F' 0 ^^ 'T' 0 ^^ 0 is is is TRUE FALSE (non-zero) (zero)

Logical Operations NOT ! FALSE ! TRUE !0 !4 !'F' !!0 !!52 is is TRUE FALSE TRUE FALSE (non-zero) (zero) (non-zero) !

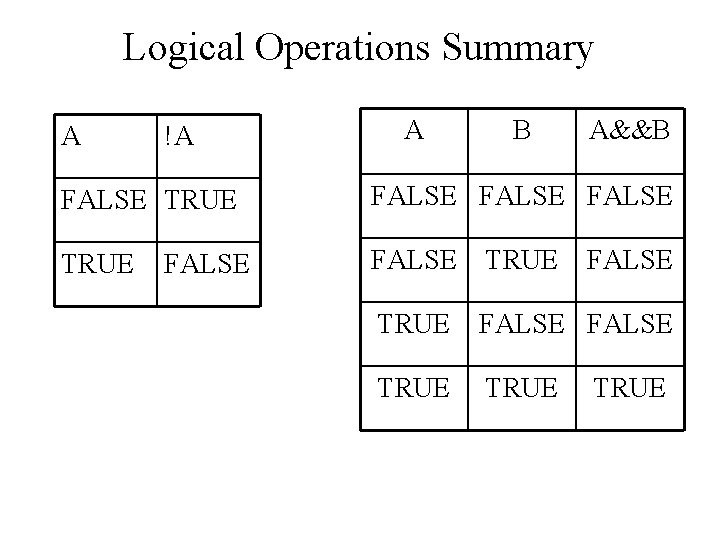
Logical Operations Summary A !A A B A&&B FALSE TRUE FALSE FALSE TRUE

Logical Operations Summary A B A||B A ^^ B FALSE FALSE TRUE FALSE TRUE TRUE TRUE FALSE

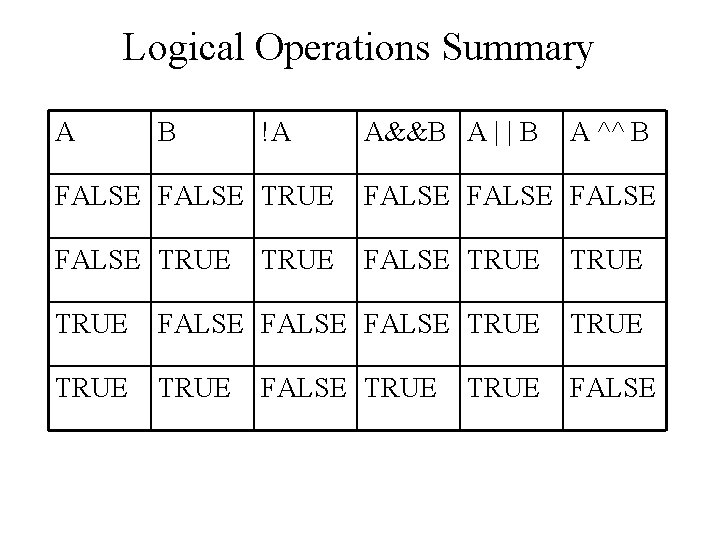
Logical Operations Summary A B !A A&&B A | | B A ^^ B FALSE TRUE FALSE TRUE FALSE TRUE FALSE TRUE

Bitwise Logical Operations • Deal with individual bits of a value • Each bit is evaluated separatly • There is no "Carry" as with addition…i. e. the results of an operation in one bit position has no effect on an adjacent bit. • Uses similar notation to Logical operators &=AND, |=OR, ^=XOR • However ~ bitwise NOT (COMPLIMENT)

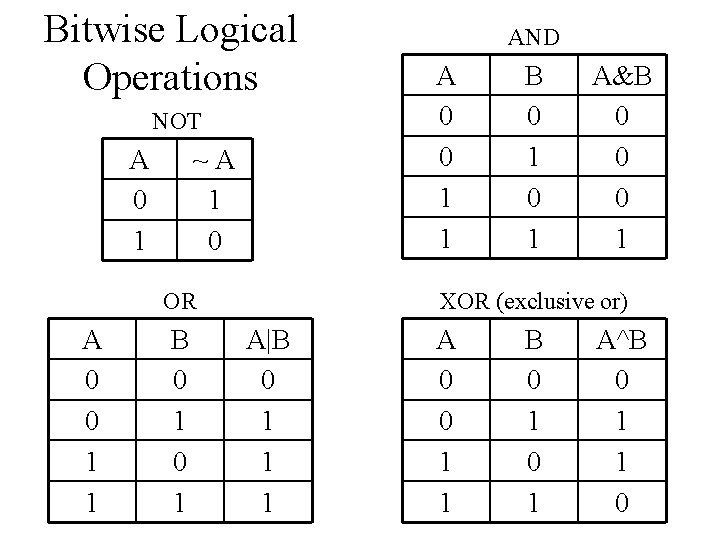
Bitwise Logical Operations NOT A 0 1 ~A 1 0 OR A 0 0 1 1 B 0 1 AND A 0 0 1 1 B 0 1 A&B 0 0 0 1 XOR (exclusive or) A|B 0 1 1 1 A 0 0 1 1 B 0 1 A^B 0 1 1 0

Bitwise Logical Operations 10111001 & 11110000 = ? 1 0 1 1 1 0 0 -------1 0 1 1 0 0 A 0 0 1 1 B 0 1 A&B 0 0 0 1

Bitwise Logical Operations 1010 & 11110000 = ? 1 0 1 0 1 1 0 0 -------- A 0 0 1 1 B 0 1 A&B 0 0 0 1

Bitwise Logical Operations 1010 & 11110000 = ? 1 0 1 0 1 1 0 0 -------1 0 0 0 A 0 0 1 1 B 0 1 A&B 0 0 0 1

Bitwise Logical Operations 10111001 | 11110000 = ? 1 0 1 1 1 0 0 -------1 1 1 0 0 1 A 0 0 1 1 B 0 1 A|B 0 1 1 1

Bitwise Logical Operations 1010 | 11110000 = ? 1 0 1 0 1 1 0 0 -------- A 0 0 1 1 B 0 1 A|B 0 1 1 1

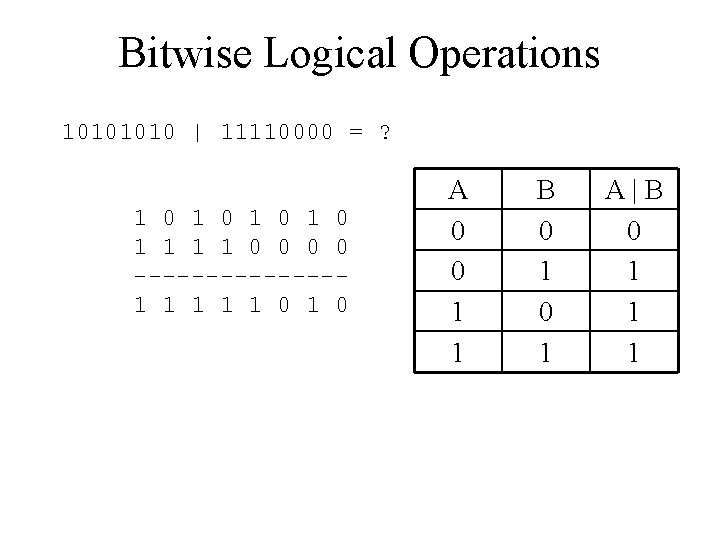
Bitwise Logical Operations 1010 | 11110000 = ? 1 0 1 0 1 1 0 0 -------1 1 1 0 A 0 0 1 1 B 0 1 A|B 0 1 1 1

Bitwise Logical Operations 10111001 ^ 11110000 = ? 1 0 1 1 1 0 0 -------0 1 0 0 1 A 0 0 1 1 B 0 1 A^B 0 1 1 0

Bitwise Logical Operations 1010 ^ 11110000 = ? 1 0 1 0 1 1 0 0 -------- A 0 0 1 1 B 0 1 A^B 0 1 1 0

Bitwise Logical Operations 1010 ^ 11110000 = ? 1 0 1 0 1 1 0 0 -------0 1 1 0 A 0 0 1 1 B 0 1 A^B 0 1 1 0

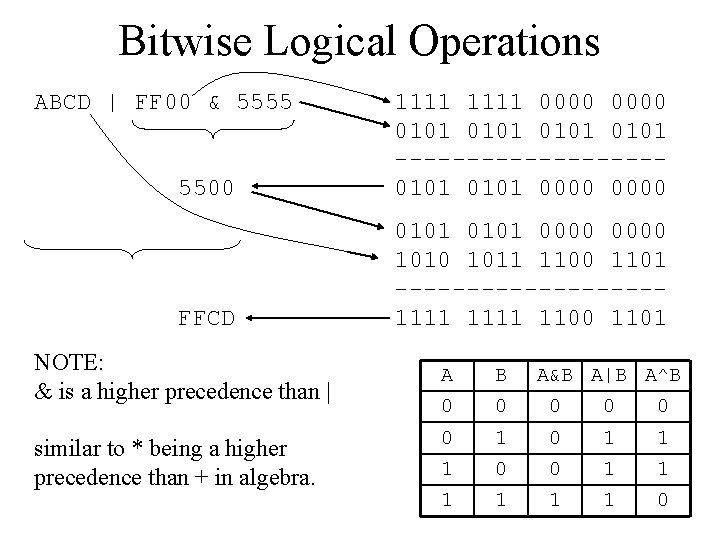
Bitwise Logical Operations ABCD | FF 00 & 5555 5500 1111 0000 0101 ---------0101 0000 FFCD 0101 0000 1010 1011 1100 1101 ---------1111 1100 1101 NOTE: & is a higher precedence than | similar to * being a higher precedence than + in algebra. A B A&B A|B A^B 0 0 0 1 0 1 1 1 0

Hex Addition 4 BA 978 + D 2 B 84 58 D 4 FC • 8+4=C • 7+8=F • 9+B=4 w/ carry • 1+A+2=D • B+D=8 w/ carry • 1+4+0=5

Hex Addition Table

Positive/Negative Numbers 1100 1011 -5 1101 -4 -3 1110 0000 1111 -2 -1 0010 0001 0 1 0100 0011 2 3 4 0101 5 Notes • We are in “ 4 -bit” mode • Think odometer math (-1=1111, -2=1110, -3=1101, -4=1100, -5=1011, -6=1010, etc. ) • At some point a big positive number+1 becomes a big negative number • Really a number “circle”

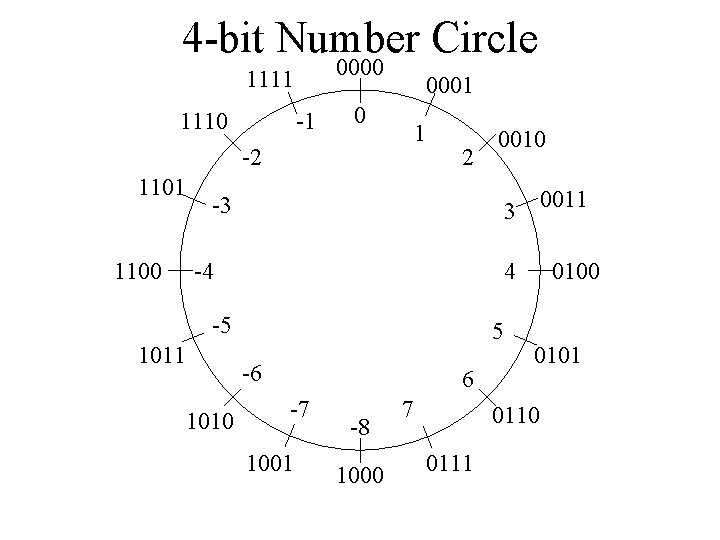
4 -bit Number Circle 0000 1111 1110 -1 0001 0 1 -2 1101 2 0010 1100 -3 -4 4 -5 1011 5 -6 1010 0011 3 6 -7 1001 -8 1000 7 0100 0101 0110 0111

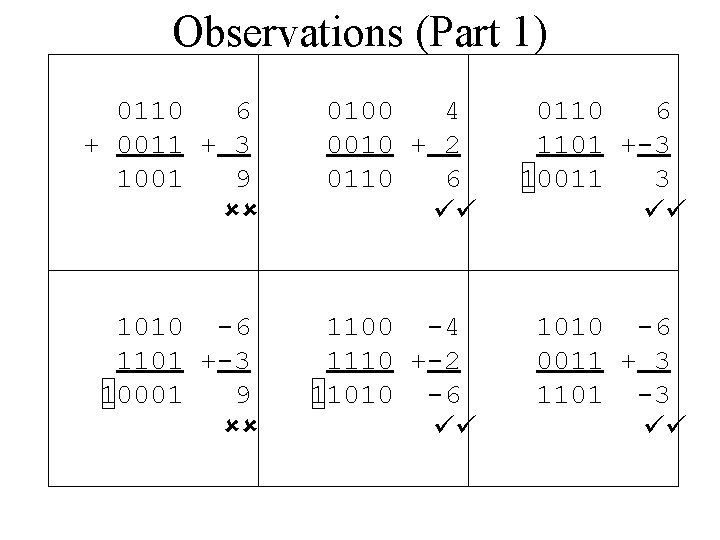
Observations (Part 1) 0110 6 + 0011 + 3 1001 9 ûû 0100 4 0010 + 2 0110 6 üü 0110 6 1101 +-3 10011 3 üü 1010 -6 1101 +-3 10001 9 ûû 1100 -4 1110 +-2 11010 -6 üü 1010 -6 0011 + 3 1101 -3 üü

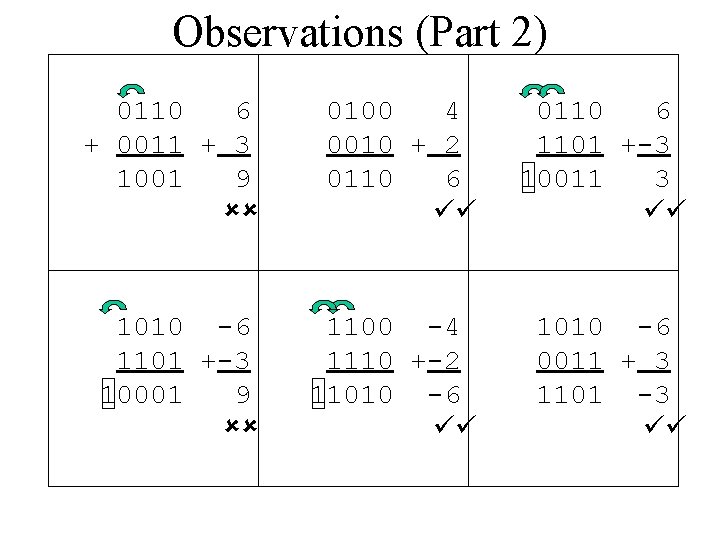
Observations (Part 2) 0110 6 + 0011 + 3 1001 9 ûû 0100 4 0010 + 2 0110 6 üü 0110 6 1101 +-3 10011 3 üü 1010 -6 1101 +-3 10001 9 ûû 1100 -4 1110 +-2 11010 -6 üü 1010 -6 0011 + 3 1101 -3 üü

Observations (Part 3) & Conclusions • Note when a carry into the sign bit occurs • Note when a carry out of the sign bit occurs • If one occurs and not the other – WRONG • If both occur – RIGHT • If neither occur – RIGHT • Therefore: OF = carry into sign bit carry out of sign bit

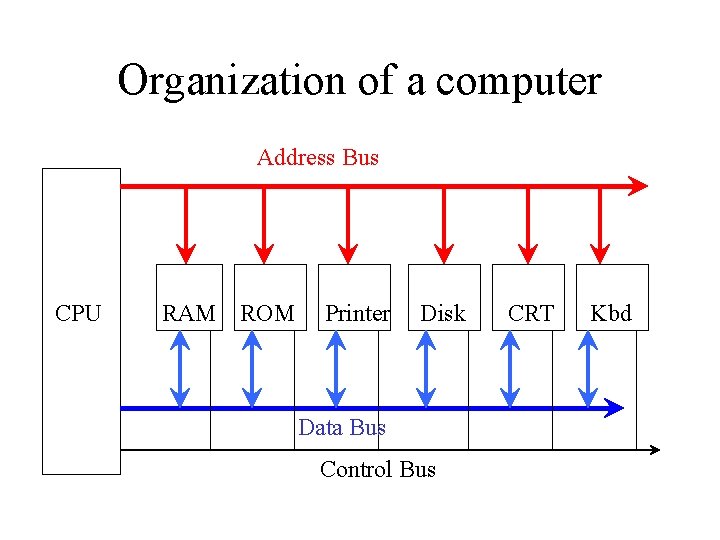
Organization of a computer Address Bus CPU RAM ROM Printer Disk Data Bus Control Bus CRT Kbd