WarmUp Convert 45 cm to km Convert 800




















- Slides: 22

Warm-Up: Convert 45 cm to km Convert 800, 000 kg to g Homework Due: Get out your crossword puzzle if you haven’t already. Fill out a yellow sheet if you are not turning your crossword puzzle in. I will check off whether or not you have your crossword puzzle/yellow sheet. If you turned it in, you have been checked off already.

Warm-Up: Convert 24 inches into centimeters. Homework Due: Get out your crossword puzzle if you haven’t already. Fill out a yellow sheet if you are not turning your crossword puzzle in. I will check off whether or not you have your crossword puzzle/yellow sheet. If you turned it in, you have been checked off already.

Objective Express your answer using the correct number of significant figures.

Agenda Review: Dimensional Analysis Practice Problems Accuracy vs Precision Significant Figures Practice with significant figures

Dimensional Analysis Review Steps: 1. Identify starting & ending units. 2. Line up conversion factors so units cancel. 3. Multiply all top numbers & divide by each bottom number. 4. Check units & answer

Example Problems 2. 4 mi = ______ ft 48 oz = ______ lb 1950 g = ______ lb

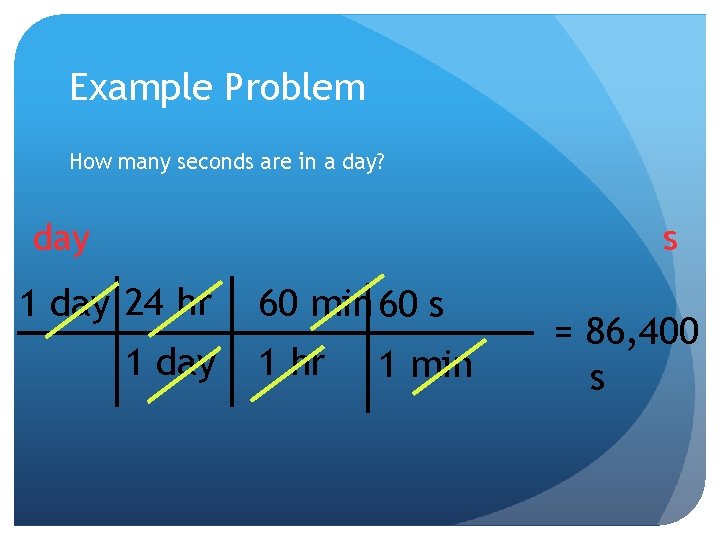
Example Problem How many seconds are in a day? s day 1 day 24 hr 1 day 60 min 60 s 1 hr 1 min = 86, 400 s

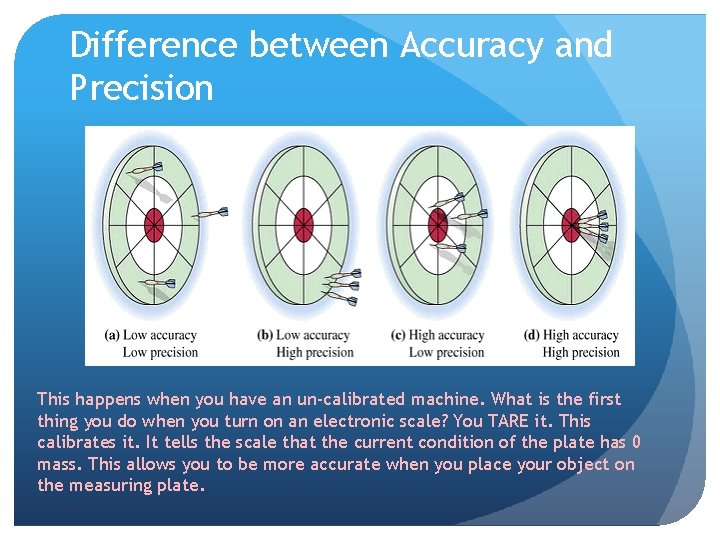
Precision vs Accuracy

Accuracy Definition: How close you are to the actual value. Is the measurement you made accurate? If an object’s true mass was 50 kg, would a measurement of 30 kg be accurate? No

Precision Definition: repeatability of a number It is the quality of the number. Has to do with significant figures The more digits you have after the decimal, the more precise your measurement is. 5. 000 m is SIGNIFICANTLY more precise than 5 m.

Difference between Accuracy and Precision This happens when you have an un-calibrated machine. What is the first thing you do when you turn on an electronic scale? You TARE it. This calibrates it. It tells the scale that the current condition of the plate has 0 mass. This allows you to be more accurate when you place your object on the measuring plate.

In Your Own Words Describe the difference between accuracy and precision OR create a visual to help explain the difference.

Significant Figures Definition: Digits that carry meaning contributing to its precision. Notice how significant figures are closely tied to precision! Recall: the more digits you have after the decimal the more precise you are.

Rules for Significant Figures: All non zero numbers are significant (meaning they count as sig figs) 613 has three sig figs 123456 has six sig figs Zeros located between non-zero digits are significant (they count) 5004 has four sig figs 602 has three sig figs 600000002 has 16 sig figs!

Rules for Significant Figures: Trailing zeros (those at the end) are significant only if the number contains a decimal point; otherwise they are insignificant (they don’t count) 5. 640 has four sig figs 120000. has six sig figs 120000 has two sig figs – unless you’re given additional information in the problem Zeros to left of the first nonzero digit are insignificant (they don’t count); they are only placeholders! 0. 000456 has three sig figs 0. 052 has two sig figs 0. 0000000000000000052 also has two sig figs!

How many significant figures are in each of the following? a) 34. 0 cm___ a) 3 b) 61400 g___ b) 3 c) 0. 002030 sec ___ c) 4 d) 6. 35 x 104 L___ d) 3 e) 4. 0 x 10 -5 kg ___ e) 2

Addition/Subtraction Your calculated value cannot be more precise than the least precise quantity used in the calculation. The least precise quantity has the fewest digits to the right of the decimal point. Your calculated value will have the same number of digits to the right of the decimal point as that of the least precise quantity.

Examples: 7. 939 6. 26 + 11. 1 25. 299 7. 939 6. 26 + 11. 1 25. 3 But, remember our rules for sig figs – we can only have as many numbers after the decimal as our least precise measurement!

Examples: 67 cm + 45 cm = ______ 6. 74 g + 2. 1 g = ______ 3. 567 m - 0. 067 m = _______

Multiplication/Division The number of sig figs in the final calculated value will be the same as that of the quantity with the fewest number of sig figs used in the calculation. Note: you are not matching the numbers after the decimal, but rather the total number of significant figures!

EXAMPLE In the example below, the quantity with the fewest number of sig figs is 27. 2 (three sig figs). Your final answer is therefore limited to three sig figs. (27. 2 x 15. 63) / 1. 846 = 230. 3011918 (this is what you calculator spits out) Round your answer to have 3 digits: 230. You must include the ending decimal!

Practice You are to complete the following worksheet for practice. If you do not finish, it will be HW.