Anisotropic nonGaussianity ar Xiv 0812 0264 Mindaugas Kariauskas

Anisotropic non-Gaussianity ar. Xiv: 0812. 0264 Mindaugas Karčiauskas work done with Konstantinos Dimopoulos David H. Lyth

Density perturbations ● Primordial curvature perturbation – a unique window to the early universe; ● Origin of structure <= quantum fluctuations; ● Usually light, canonically normalized scalar fields => statistical homogeneity and isotropy; ● Statistically anisotropic perturbations from the vacuum with a broken rotational symmetry; ● The resulting observable. is anisotropic and may be

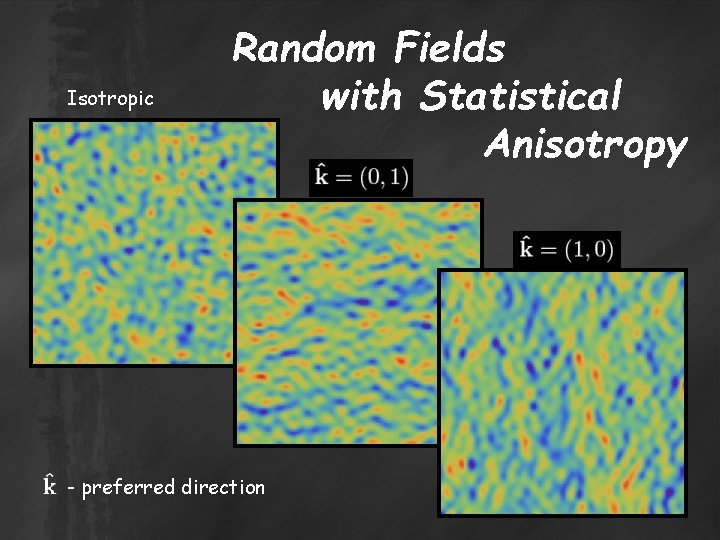
Statistical homogeneity and isotropy ● Density perturbations – random fields; ● Density contrast: ; ● Multipoint probability distribution function : ● Homogeneous if the same under translations of all ● Isotropic if the same under spatial rotation; ;

Statistical homogeneity and isotropy ● Assume statistical homogeneity; ● Two point correlation function ● Isotropic if for ; ● The isotropic power spectrum: ● The isotropic bispectrum:

Statistical homogeneity and isotropy ● Two point correlation function ● Anisotropic if even for ● The anisotropic power spectrum: ● The anisotropic bispectrum: ;

Isotropic Random Fields with Statistical Anisotropy - preferred direction

Present Observational Constrains ● The power spectrum of the curvature perturbation: & almost scale invariant; ● Non-Gaussianity from WMAP 5 (Komatsu et. al. (2008)): ● No tight constraints on anisotropic contribution yet; ● Anisotropic power spectrum can be parametrized as ● Present bound (Groeneboom, Eriksen (2008)); ● We have calculated of the anisotropic curvature perturbation - new observable.

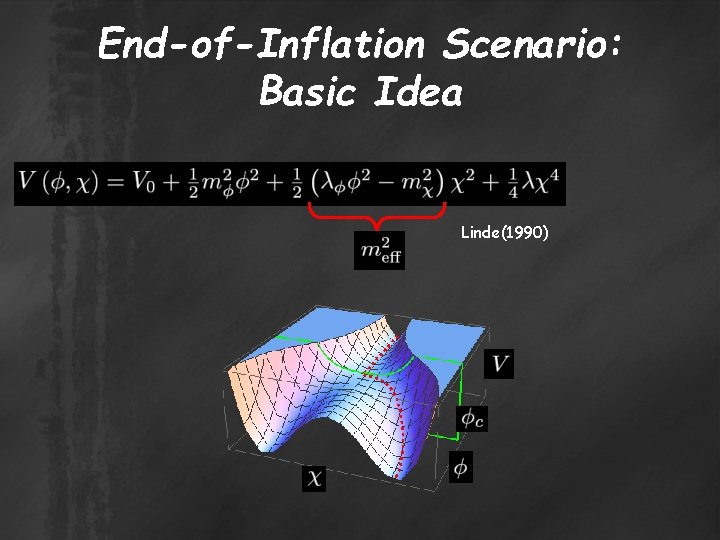
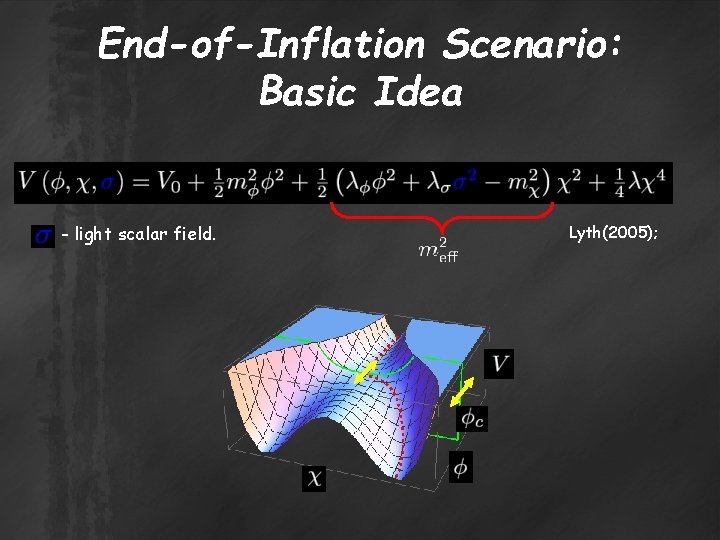
Origin of Statistically Anisotropic Power Spectrum ● Homogeneous and isotropic vacuum => the statistically isotropic perturbation; ● For the statistically anisotropic perturbation <= a vacuum with broken rotational symmetry; ● Vector fields with non-zero expectation value; ● Particle production => conformal invariance of massless U(1) vector fields must be broken; ● We calculate for two examples: ● End-of-inflation scenario; ● Vector curvaton model.

δN formalism ● To calculate we use formalism (Sasaki, Stewart (1996); Lyth, Malik, Sasaki (2005)); ● Recently in was generalized to include vector field perturbations (Dimopoulos, Lyth, Rodriguez (2008)): where , , etc.

End-of-Inflation Scenario: Basic Idea Linde(1990)

End-of-Inflation Scenario: Basic Idea - light scalar field. Lyth(2005);

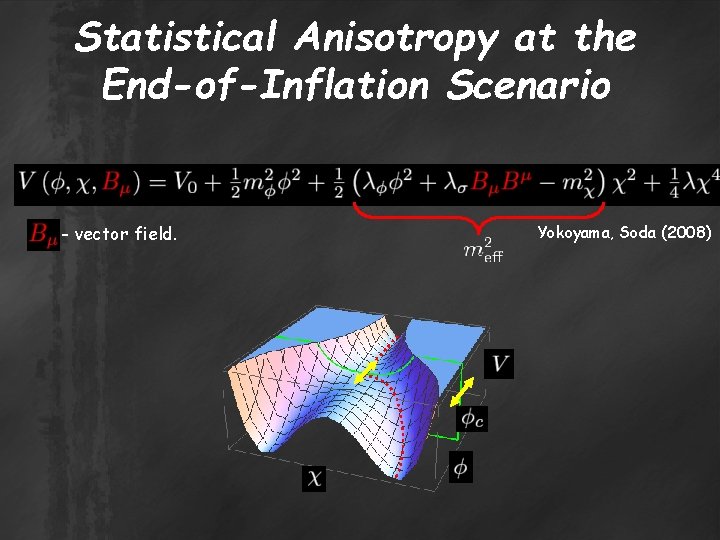
Statistical Anisotropy at the End-of-Inflation Scenario - vector field. Yokoyama, Soda (2008)

Statistical Anisotropy at the End-of-Inflation Scenario ● ● ● Physical vector field: Non-canonical kinetic function Scale invariant power spectrum => Only the subdominant contribution; Non-Gaussianity: where , - slow roll parameter ; ;

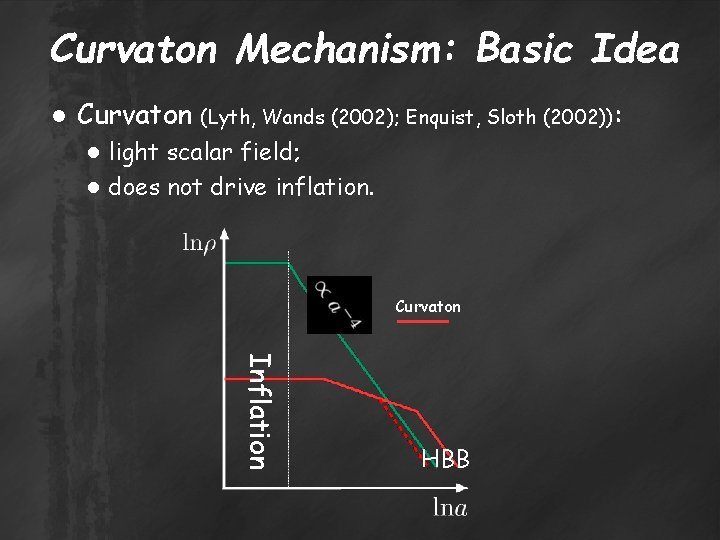
Curvaton Mechanism: Basic Idea ● Curvaton (Lyth, Wands (2002); Enquist, Sloth (2002)): ● light scalar field; ● does not drive inflation. Curvaton Inflation HBB

Vector Curvaton ● Vector field acts as the curvaton field (Dimopoulos (2006)); ● Only a small contribution to the perturbations generated during inflation; ● Assuming: ● scale invariant perturbation spectra; ● no parity braking terms; ● Non-Gaussianity: where

Estimation of ● In principle isotropic perturbations are possible from vector fields; ● In general power spectra will be anisotropic => must be subdominant ( ); ● For subdominant contribution can be estimated on a fairly general grounds; ● All calculations were done in the limit ● Assuming that one can show that ;

Conclusions ● We considered anisotropic contribution to the power spectrum and ● calculated its non-Gaussianity parameter . ● We applied our formalism for two specific examples: end -of-inflation and vector curvaton. ●. is anisotropic and correlated with the amount and direction of the anisotropy. ● The produced non-Gaussianity can be observable: ● Our formalism can be easily applied to other known scenarios. ● If anisotropic is detected => smoking gun for vector field contribution to the curvature perturbation.