ALGORYTMY I STRUKTURY DANYCH WYKAD 12 Techniki konstruowania

ALGORYTMY I STRUKTURY DANYCH WYKŁAD 12 Techniki konstruowania algorytmów – przykłady Grażyna Mirkowska PJWSTK, 2002/2003 czerwiec 2003 G. Mirkowska, ASD_12 Progamowanie dynamiczne

Plan wykładu Kody Huffmana 4 Mnożenie macierzy 4 Najdłuższy wspólny podciąg 4 czerwiec 2003 G. Mirkowska, ASD_12 Progamowanie dynamiczne 2

Problem kodowania Dany jest ciąg znaków. Chcemy tak zapisać ten ciąg w taki sposób, by zajmował jak najmniej miejsca i by dało się go potem łatwo odtworzyć. Znak = liczba 0 -255, czyli 8 bitów 100 000 znaków zajmuje 800 000 bitów. Jeśli w naszych danych występuje tylko 6 różnych znaków, to 3 bity wystarczą do ich zakodowania, 100 000 znaków zajmuje 300 000 bitów. np. : 000, 001, 010, 011, 100, 101 czerwiec 2003 G. Mirkowska, ASD_12 Progamowanie dynamiczne 3

Kody stałej i zmiennej długości Kody o stałej długości -wszystkie słowa kodowe mają tę samą długość Znaki występujące często powinny mieć kod możliwie krótki. Kody o zmiennej długości -długość słowa kodowego zależy od częstości występowania danego znaku w ciągu danych. Przykład Niech będzie tekst 100000 znakowy, w którym występują tylko litery a, b, c, d, e, f i a-45 tys razy, b-13 tys. , c-12 tys. , d-16 tys. , e - 9 tys. , f-5 tys. razy. czerwiec 2003 Używając kodu a= 0, b= 101, c= 100, d=111, e=1101, f=1100 nasz tekst można zakodować na 224000 bitach. G. Mirkowska, ASD_12 Progamowanie dynamiczne 4

Kody prefiksowe ZASADA Żadne słowo kodowe nie jest prefiksem żadnego innego słowa kodowego. Chodzi o to by można było jednoznacznie odczytać zakodowany tekst. czerwiec 2003 tzn. nie istnieją takie dwa słowa a i b, a=(a 1, . . . an), b=(b 1, b 2. . . , bm) n<m , że dla pewnego i n a 1= b 1, a 2= b 2. . . , ai = bi Twierdzenie Jeśli istnieje optymalne kodowanie, to zawsze można znaleźć kod prefiksowy, który go realizuje. G. Mirkowska, ASD_12 Progamowanie dynamiczne 5

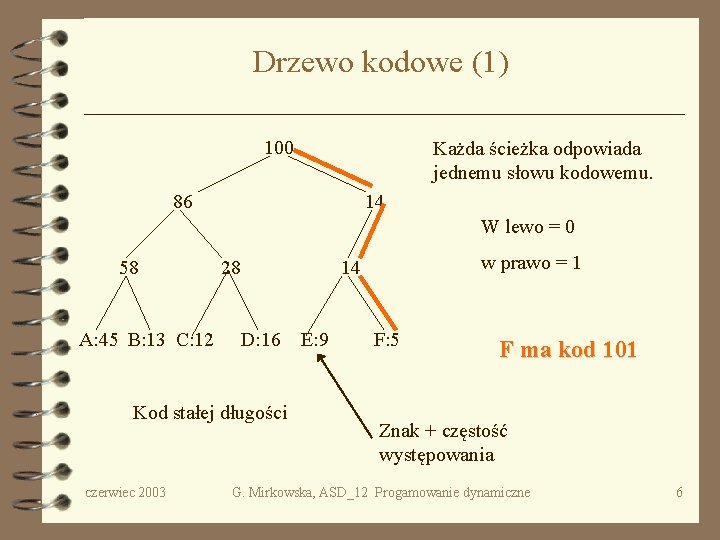
Drzewo kodowe (1) 100 Każda ścieżka odpowiada jednemu słowu kodowemu. 86 14 W lewo = 0 58 A: 45 B: 13 C: 12 28 D: 16 Kod stałej długości czerwiec 2003 w prawo = 1 14 E: 9 F: 5 F ma kod 101 Znak + częstość występowania G. Mirkowska, ASD_12 Progamowanie dynamiczne 6

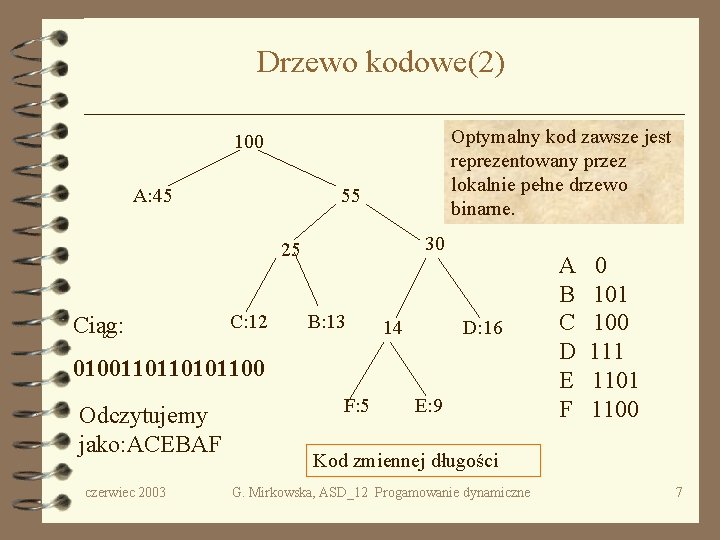
Drzewo kodowe(2) Optymalny kod zawsze jest reprezentowany przez lokalnie pełne drzewo binarne. 100 A: 45 55 30 25 Ciąg: C: 12 B: 13 14 D: 16 01001101100 Odczytujemy jako: ACEBAF czerwiec 2003 F: 5 E: 9 A B C D E F 0 101 100 111 1100 Kod zmiennej długości G. Mirkowska, ASD_12 Progamowanie dynamiczne 7

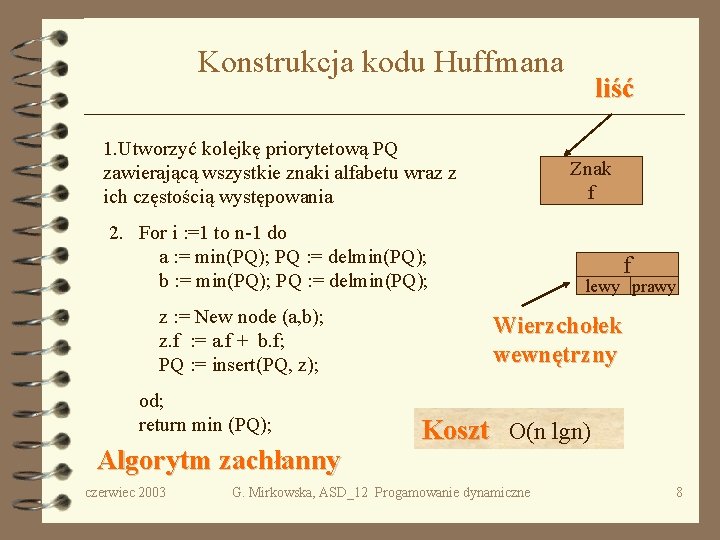
Konstrukcja kodu Huffmana 1. Utworzyć kolejkę priorytetową PQ zawierającą wszystkie znaki alfabetu wraz z ich częstością występowania Znak f 2. For i : =1 to n-1 do a : = min(PQ); PQ : = delmin(PQ); b : = min(PQ); PQ : = delmin(PQ); z : = New node (a, b); z. f : = a. f + b. f; PQ : = insert(PQ, z); od; return min (PQ); Algorytm zachłanny czerwiec 2003 liść f lewy prawy Wierzchołek wewnętrzny Koszt O(n lgn) G. Mirkowska, ASD_12 Progamowanie dynamiczne 8

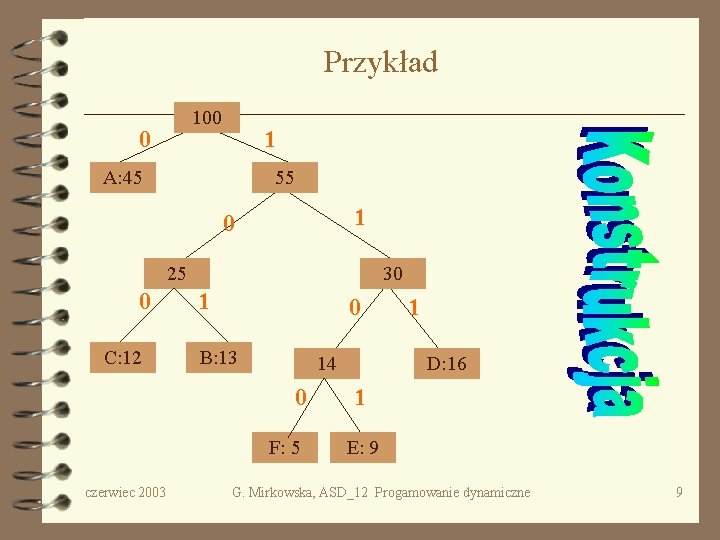
Przykład 100 0 1 A: 45 55 1 0 25 30 1 0 C: 1214 B: 13 14 C: 12 B: 13 14 D: 16 14 0 F: 5 czerwiec 2003 E: 9 A: 45 30 1 D: 16 25 D: 16 A: 45 1 E: 9 D: 16 C: 12 F: 5 B: 13 F: 5 C: 12 E: 9 B: 13 A: 45 G. Mirkowska, ASD_12 Progamowanie dynamiczne 9

Mnożenie macierzy Dany jest ciąg macierzy A 1, A 2, . . . , An. Obliczyć iloczyn A 1 A 2 . . . An tak by koszt mnożenia był najmniejszy. Przykład Obliczyć A B C. A(10 100) B(100 5) C(5 50) (A B) C = A ( B C) Koszt lewej strony = (10 *100*5 ) + (10*5*50)= 7500 mnożeń skalarnych czerwiec 2003 Uwaga: Możemy pomnożyć macierz A przez B wttw gdy A ma tyle kolumn ile B wierszy. Koszt(A B) = A. w *A. k* B. w Koszt prawej strony = (100 *5*5 0) + (10*100*50) = 75000 mnożeń skalarnych G. Mirkowska, ASD_12 Progamowanie dynamiczne 10

Prosty Algorytm? Rozważyć wszystkie możliwe ustawienia nawiasów w ciągu, a potem wykonać mnożenia zgodnie z ustawieniem nawiasów. Za duży koszt! Za każdym razem wyliczyć koszt mnożenia przy danym ustawieniu nawiasów i wybrać to ustawienie, które ma koszt najmniejszy. n-1 sza liczba Catalana (4 n/n 3/2) A ile jest możliwych ustawień nawiasów? Niech P(n) będzie liczbą ustawień nawiasów w ciągu n elementowym. czerwiec 2003 (A 1, . . . , Ak) ( Ak+1, . . . , An) G. Mirkowska, ASD_12 Progamowanie dynamiczne 11

Paradygmat programowania dynamicznego 1. Scharakteryzować strukturę rozwiązania optymalnego. Rozwiązanie optymalne zawiera w sobie optymalne rozwiązania dla podproblemów. W naszym przykładzie: dla pewnego k, policzymy najpierw optymalne ustawienie nawiasów dla iloczynu (A 1, . . . , Ak) potem optymalne ustawienie nawiasów dla iloczynu (Ak+1. . , An), a potem dodamy do tego koszt mnożenia 2 macierzy. 2. Zdefiniować rekurencyjnie wartość rozwiązania optymalnego, jako funkcję rozwiązań optymalnych dla podproblemów. czerwiec 2003 G. Mirkowska, ASD_12 Progamowanie dynamiczne 12

Liczymy minimalny koszt Niech m[i, j] będzie minimalną liczbą mnożeń skalarnych potrzebnych do policzenia iloczynu ( Ai. . , Aj), oraz macierz Ai ma wymiar (p i-1 pi). Niech s[i, j] = k, gdzie k realizuje minimum dla m[i, j]. Rekurencyjny algorytm obliczania m[i, j] nie jest możliwy do zastosowania, bo jego koszt jest wykładniczy, ale. . . czerwiec 2003 Przecież można zapamiętywać policzone wcześniej wartości m[i, j]! G. Mirkowska, ASD_12 Progamowanie dynamiczne 13

Algorytm MCM Ustawienie początkowej wartości elementów tablicy m. for i : =1 to n do m[i, i] : =0; od; for x : = 2 to n do for i : = 1 to n-x+1 do j : = i+x-1 Dwie pętle odpowiedzialne za wypełnienie wszystkich elementów m[i, j] : = + ; for k : = i to j-1 do q : = m[i, k]+m[k+1, j] + pi-1*pk *pj; if q < m[i, j] then m[i, j] : = q; s[i, j] : =k fi od Wyszukiwanie od minimum od return m, s; 3 Koszt O(n ) czerwiec 2003 G. Mirkowska, ASD_12 Progamowanie dynamiczne 14

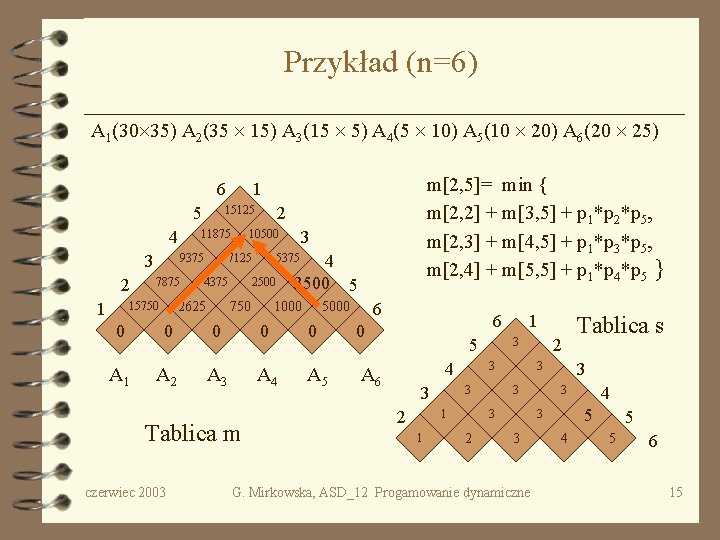
Przykład (n=6) A 1(30 35) A 2(35 15) A 3(15 5) A 4(5 10) A 5(10 20) A 6(20 25) 6 5 4 3 2 1 11875 7875 3 10500 7125 4375 2625 15750 2 15125 9375 m[2, 5]= min { m[2, 2] + m[3, 5] + p 1*p 2*p 5, m[2, 3] + m[4, 5] + p 1*p 3*p 5, m[2, 4] + m[5, 5] + p 1*p 4*p 5 } 1 4 3500 5 5375 2500 750 1000 5000 6 0 0 0 A 1 A 2 A 3 A 4 A 5 A 6 Tablica m czerwiec 2003 6 5 4 3 2 3 3 G. Mirkowska, ASD_12 Progamowanie dynamiczne 4 3 5 3 3 Tablica s 3 3 3 2 2 3 3 1 1 1 4 5 5 6 15

W jakiej kolejności mnożyć? Zasada 3 paradygmatu programowania dynamicznego: Skonstruować rozwiązanie problemu na bazie wyliczonych wielkości. mnóż(A, s, i, j) { If j>i then } W naszym przykładzie : Mnóż (A, s, 1, 6) daje : (A 1(A 2 A 3))((A 4 A 5) A 6) X : = mnóż(A, s, i, s[i, j]); Y: = mnóż(A, s, s[i, j]+1, j); return wynik mnożenia macierzy (X Y) else return Ai czerwiec 2003 G. Mirkowska, ASD_12 Progamowanie dynamiczne 16

Najdłuższy wspólny podciąg Dane są dwa ciągi znaków X i Y X=(x 1, …xm) Y = (y 1, …, yn) Znaleźć taki ciąg Z=(z 1, …zk), że Z jest najdłuższym podciągiem zarówno ciągu X jak i Y, ozn. Z = nwp(X, Y) • Wygenerować wszystkie podciągi ciągu X. Przykład X = aawbbsccpddólnvby Y = xxwsyyypózzlinsy nwp(X, Y) = wspólny czerwiec 2003 Ale zbyt ciągów dużo sprawdzić • Dla każdegotoz tych czy występuje wkosztuje Y, zapamiętując O(2 m) z takich jednocześnie najdłuższy ciągów. G. Mirkowska, ASD_12 Progamowanie dynamiczne 17

Analiza zadania Oznaczenie: Xi = (x 1, …xi) Niech X= (x 1, …xm) Y= (y 1, …, yn) oraz nwp(X, Y) = Z , gdzie Z= (z 1, …zk). Jeżeli xm= yn, wtedy zc=xm=yn oraz Z k-1= nwp(Xm-1, Yn-1). Jeżeli xm yn, wtedy Z = nwp(Xm-1, Y), gdy zk xm oraz Z = nwp(X, Yn-1), gdy zk yn. Abrakadabra barakuda czerwiec 2003 Abrakadabrb arakud k d Abrakad barakud a Abraka baraku G. Mirkowska, ASD_12 Progamowanie dynamiczne itd 18

Algorytm 2 konkatenacja Function nwp(X, Y : string) : string; begin if x(m)=y(n) then Z : = nwp(X m-1 1, Y n-1)o x(m) else Z 1 : = nwp(X m-1, Y); Z 2 : = nwp(X, Y n-1); Z : = dluższy z ciągów Z 1 i Z 2; fi end; czerwiec 2003 Koszt tego algorytmu będzie w najgorszym razie wykładniczy. G. Mirkowska, ASD_12 Progamowanie dynamiczne 19

Jak wyliczyć długość nwp(X, Y)? długość najdłuższego wspólnego podciągu ciągów X, Y. d(X, Y) = d( X m-1 , Y n-1 ) +1, gdy xm=yn d(X, Y) = max (d(X m-1 , Y), d(X , Y n-1 ), gdy xm yn Przykład 1 B 1 A 0 2 B 11 3 C 1 czerwiec 2003 2 D 00 1 1 3 C 0 1 2 4 A 1 1 2 5 6 B A 1 2 2 2 Koszt obliczenia d(X, Y) wynosi card(X) * card(Y) porównań. G. Mirkowska, ASD_12 Progamowanie dynamiczne 20

Algorytm Begin for i : =1 to m do d(i, 0): =0 od; for j : =0 to n do d(0, j) : = 0 od; for i : =1 to m do for j : =1 to n do if x(i)=y(j) then d(i, j) : = d(i-1, j-1) +1; b(i, j) : = „” else if d(i-1, j) d(i, j-1) then d(i, j) : = d(i-1, j); b(i, j) : = „ ” else d(i, j) : = d(i, j-1); b(i, j) : = „ ” fi fi od od end czerwiec 2003 Po przekątnej zadanie, które trzeba rozwiązać, żeby otrzymać optymalny wynik. „w górę” zadanie, które trzeba rozwiązać, żeby otrzymać optymalny wynik „w lewo” zadanie, które trzeba rozwiązać, żeby otrzymać optymalny wynik G. Mirkowska, ASD_12 Progamowanie dynamiczne 21

Wypisanie nwp Procedure Drukuj(b, i, j); begin if i=0 or j=0 then return fi; if b(i, j) = „” then call drukuj(b, i-1, j-1); write(x(i)) else if b(i, j) = „ ” then call drukuj(b, i-1, j) else call drukuj (b, i, j-1) fi fi end czerwiec 2003 Przykład b(i, j) 1 B 0 1 A 00 0 2 B 0 11 3 C 0 1 4 B 0 1 5 D 0 1 6 A 0 2 7 B 0 1 2 D 0 0 11 1 1 2 2 2 G. Mirkowska, ASD_12 Progamowanie dynamiczne 3 4 5 6 C A B A 0 0 0 1 1 2 2 2 2 2 3 3 4 44 2 3 4 44 22