ALGORYTMY I STRUKTURY DANYCH WYKAD 05 c d

ALGORYTMY I STRUKTURY DANYCH WYKŁAD 05 c. d. Sortowanie Grażyna Mirkowska PJWSTK, 2003/2004 G. Mirkowska, ASD_05 Sortowanie c. d.

Plan wykładu Drzewa decyzyjne Dolne oszacowanie złożoności problemu sortowania przez porównywanie elementów 4 Sortowanie z kosztem liniowym 4 4 – – 2021 -12 -17 Sortowanie koszykowe Sortowanie przez zliczanie G. Mirkowska, ASD_05 Sortowanie c. d. 2

Drzewo decyzyjne Niech SORT oznacza dowolny algorytm rozwiązujący problem sortowania przez porównywanie elementów. Drzewem decyzyjnym dla algorytmu SORT nazywamy drzewo lokalnie pełne (tzn. każdy wierzchołek ma 0 albo 2 następniki) takie, że - etykietami wierzchołków są zdania opisujące relacje między elementami, - etykietami liści są uporządkowane permutacje wynikające z relacji między elementami na ścieżce prowadzącej do tego liścia. 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 3

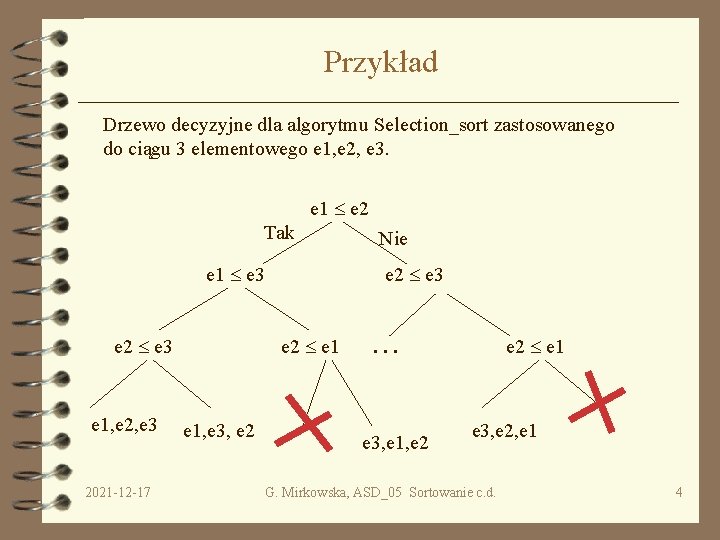
Przykład Drzewo decyzyjne dla algorytmu Selection_sort zastosowanego do ciągu 3 elementowego e 1, e 2, e 3. e 1 e 2 Tak e 1 e 3 e 2 e 3 e 1, e 2, e 3 2021 -12 -17 e 2 e 3 e 2 e 1, e 3, e 2 Nie e 2 e 1 . . . e 3, e 1, e 2 e 3, e 2, e 1 G. Mirkowska, ASD_05 Sortowanie c. d. 4

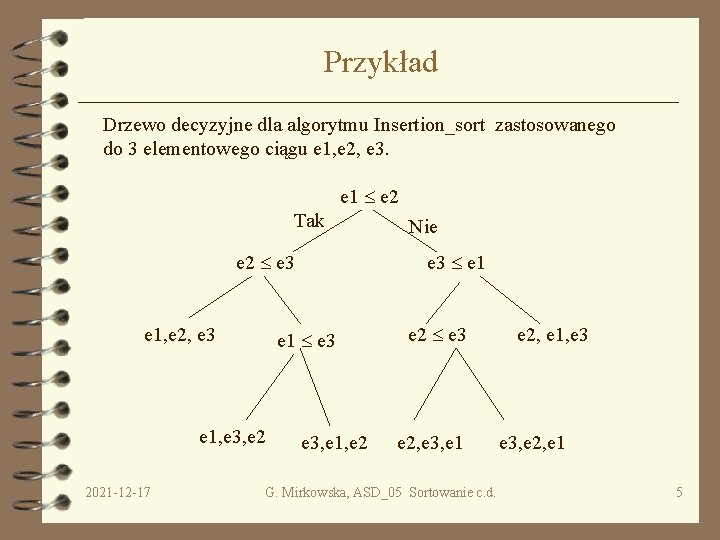
Przykład Drzewo decyzyjne dla algorytmu Insertion_sort zastosowanego do 3 elementowego ciągu e 1, e 2, e 3. e 1 e 2 Tak e 2 e 3 e 1, e 2, e 3 2021 -12 -17 e 3 e 1 e 3 e 1, e 3, e 2 Nie e 3, e 1, e 2 e 3 e 2, e 3, e 1 G. Mirkowska, ASD_05 Sortowanie c. d. e 2, e 1, e 3, e 2, e 1 5

Własności drzew decyzyjnych Jeżeli f jest liczbą liści w drzewie binarnym, a h jego wysokością, to (i) f 2 h h (ii) h lg f h+1 y (i) Indukcja po h. y=Nie- liście na poziomie h Krok indukcyjny: f 2 y + (2 h - y) = y+2 h + 2 h (ii) Z (i) przez logarytmowanie. 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 6

Oszacowanie w najgorszym przypadku Każde drzewo decyzyjne dla algorytmu sortującego ciąg nelementowy przez porównywanie elementów, ma co najmniej wysokość log n! Drzewo decyzyjne ma co najmniej n! liści. Stąd i z lematu 1 - teza Każdy algorytm sortujący ciąg n elementowy przez porównywanie elementów musi wykonać co najmniej log n! porównań w najgorszym wypadku. W(n) n lg n 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 7

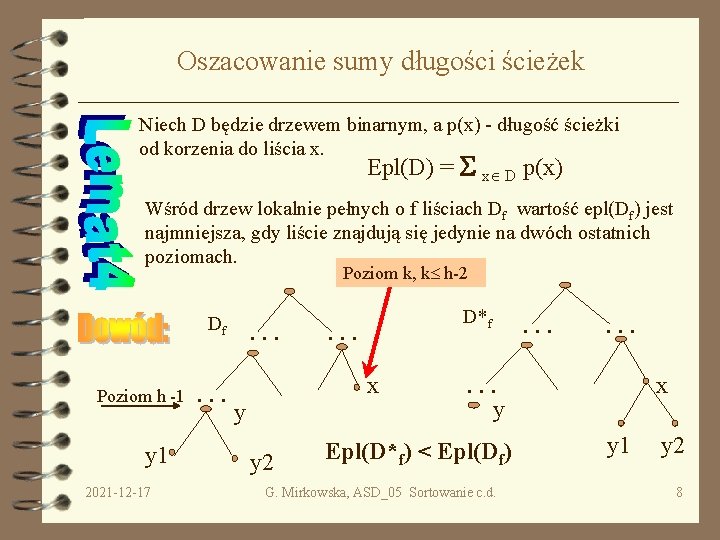
Oszacowanie sumy długości ścieżek Niech D będzie drzewem binarnym, a p(x) - długość ścieżki od korzenia do liścia x. Epl(D) = S x D p(x) Wśród drzew lokalnie pełnych o f liściach Df wartość epl(Df) jest najmniejsza, gdy liście znajdują się jedynie na dwóch ostatnich poziomach. Poziom k, k h-2 Df Poziom h -1 y 1 2021 -12 -17 . . . D*f . . . x y y 2 . . y Epl(D*f) < Epl(Df) G. Mirkowska, ASD_05 Sortowanie c. d. x y 1 y 2 8

Minimalne epl. Min {epl(Df): Df D}= f lg f + 2( f-2 lg f ) Niech Df będzie drzewem, dla którego epl osiąga minimum. Przypadek 1 f = 2 p. Df 2021 -12 -17 Wszystkie liście są na poziome p Poziom p epl(Df)= f * lg f G. Mirkowska, ASD_05 Sortowanie c. d. 9

Minimalne epl c. d. Przypadek 2 2 p-1 < f < 2 p. Z lematu 1 h lg f Df h Epl(Df)= x (h-1) + z h = x z Z lematu 3 wszystkie liście są na poziomach h i h-1. Czyli h = lg f. Liście na poziomie h-1 x=f-z = (2 h -f)(h-1) + (2 f -2 h) h = hf + f - 2 h Liście na poziomie h z =2( 2 h-1 - x) 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 10

Koszt średni Średnia liczba porównań wykonywanych przez dowolny algorytm sortujący ciąg nelementowy przez porównywanie elementów jest nie mniejsza niż lg n! . Średnia wysokość drzewa decyzyjnego h epl min(D)/n! h (n! lg n! + 2( n!-2 lg n! ))/n! Ale dla dowolnego x, x/2 2 lgx x Ale 2( n!-2 lg n! )/n! 0 h lg n! 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 11

Wniosek Dolnym ograniczeniem na liczbę porównań wykonanych przez algorytm sortujący przez porównywanie elementów jest w przypadku średnim (n lg n). Algorytm Quick. Sort jest optymalnym algorytmem ze względu na średnią złożoność czasową. 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 12

Sortowanie z kosztem liniowym Załóżmy, że dane wejściowe a[1], . . . , a[n] są generowane losowo z rozkładem jednorodnym oraz że a[i] {0, . . . , k-1} dla pewnej ustalonej (niezbyt dużej) liczby k. Krok 1. Utworzyć k pustych koszyków o numerach od 0 do k-1. Krok 2 i-ty element ciągu wkładamy do koszyka o numerze a[i]. Krok 3. Wyjmujemy elementy z kolejnych koszyków od 0 do k-1, otrzymując posortowany ciąg. (k) Czasu na tworzenie koszyków (n) Czasu na rozrzucanie elementów 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 13

Sortowanie przez zliczanie Założenie: dany n elementowy ciąg o elementach z przedziału [1, k], k N. Metoda polega na znalezieniu dla każdego x liczby elementów mniejszych równych niż x. Pozwoli to ustalić właściwą pozycję x w tablicy wyjściowej. 7 ma trafić na pozycję 5, bo są 4 elementy od niej mniejsze 6 7 3 2 9 1 8 Powinna trafić na pozycje 4, bo są 3 liczby mniejsze 1 2 3 4 5 6 7 3 powinna trafić na pozycje trzecią, bo są 2 elementy mniejsze od niej 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 14

Sortowanie przez zliczanie { // a- tablica danych, B tablica wyników, C tablica pomocnicza. for i : = 1 to k do C[i] : = 0 od; for j : = 1 to n do C[a[j]] : = C[a[j]] +1 od; for i : = 2 to k do C[i] = liczba elementów równych i C[i] : = C[i] + C[i-1] od; C[i] = liczba elementów mniejszych równych i for j : = n downto 1 do B[C[a[j]]] : = a[j]; C[a[j]] : = C[a[j]] – 1 od; } 2021 -12 -17 Na lewo od pozycji C[a[j]] leżą elementy od a[j], a na prawo > a[j]. C[a[j]] wskazuje liczbę jeszcze nie wpisanych elementów a[j] O(k+n) Stabilność algorytmu G. Mirkowska, ASD_05 Sortowanie c. d. 15

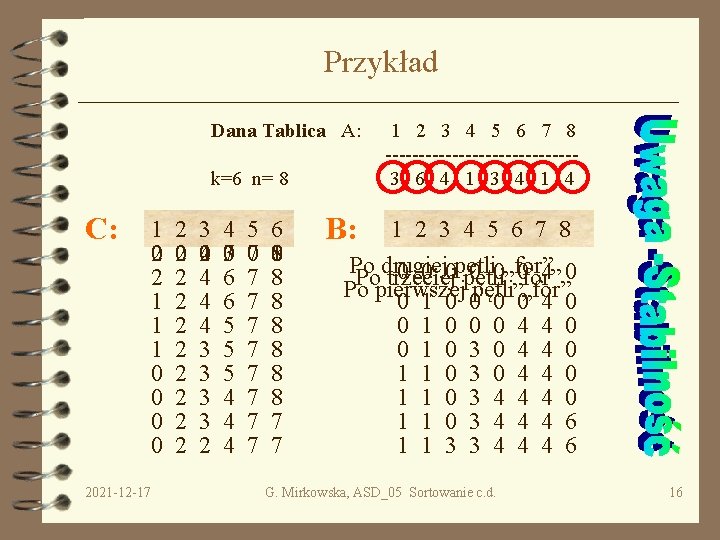
Przykład Dana Tablica A: k=6 n= 8 C: 2021 -12 -17 1 20 2 1 1 1 0 0 2 20 2 2 2 2 3 420 4 4 4 3 3 2 4 730 6 6 5 5 5 4 4 4 5 70 7 7 7 7 6 810 8 8 8 7 7 B: 1 2 3 4 5 6 7 8 --------------3 6 4 1 3 4 1 2 3 4 5 6 7 8 Po drugiej 0 0 0 pętli 0 0„for” 0 4 0 Po trzeciej pętli „for” Po pierwszej 0 1 0 0 pętli 0 0„for” 4 0 0 1 0 0 0 4 4 0 0 1 0 3 0 4 4 0 1 1 0 3 4 4 4 6 1 1 3 3 4 4 4 6 G. Mirkowska, ASD_05 Sortowanie c. d. 16

Sortowanie pozycyjne Dany jest ciąg n-elementów do posortowania. Elementy tego ciągu nie są po prostu liczbami naturalnymi, lecz same mają wewnętrzną strukturę, np. . są to skończone ciągi pewnych obiektów (np. . Liczb, cyfr, znaków itd. . ). Metoda naiwnego rozrzucania Rozrzucić elementy danego ciągu do „koszyków” ze względu na kolejne pozycje w ciągach składowych, tzn. tworzymy pewną liczbę „koszyków” , tak, że i-ty koszyk odpowiada i-tej pozycji w ciągach składowych. Następnie sortujemy każdy z koszyków osobno tą samą metodą. 2021 -12 -17 Takie postępowanie jest kosztowne: Dla elementów, które są ciągami liczb o d cyfrach, trzeba utworzyć 10 d koszyków! Takie postępowanie zawsze daje poprawny wynik np. gdy ciągi nie są równej długości. G. Mirkowska, ASD_05 Sortowanie c. d. 17

Radix-Sort Dane : tablica n-liczb całkowitych o d cyfrach. For k : = 1 to d do // rozrzuć wszystkie liczby do ‘kubełków’ o numerach //0, 1, 2, . . . , 9 ze względu na k-tą od końca cyfrę. //połącz kubełki w jeden ciąg. od T(n) = O(d* n) 2021 -12 -17 Wszystkie elementy, obcięte do k-1 ostatnich pozycji, tworzą ciąg uporządkowany niemalejąco. G. Mirkowska, ASD_05 Sortowanie c. d. 18

Radix-sort Dany ciąg : 85 83 63 64 84 15 63 83 84 64 15 85 Stos 3 Stos 4 Stos 5 Po połączeniu : 63 83 84 64 15 85 15 Stos 1 64 63 Stos 6 85 84 83 Stos 8 Po połączeniu : 15 64 63 85 84 83 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 19

c. d. Radix Sort For k : = 1 to d do For k : = 1//to d do elementy ze względu na ktą od posortuj Użyjmy // rozrzuć wszystkie dostosując ‘kubełków’ końca liczby pozycję jakiśostabilny //numerach 0, algorytm, //1, 2, . . . 9 zenp. algorytm względu na k-tą kolejek jako //od końca cyfrę. Counting. Sort // ‘kubełków’! //połącz odkubełki w jeden ciąg. od Dany ciąg : 85 83 63 64 84 15 2021 -12 -17 Kolejka 3: 83 63 Kolejka 4: 64 84 Kolejka 5: 85 15 Kolejka 1: 15 Kolejka 6: 63 64 Kolejka 8: 83 84 85 83 63 64 84 85 15 15 63 64 83 84 85 G. Mirkowska, ASD_05 Sortowanie c. d. 20

Poprawność Algorytm Radix. Sort zaimplementowany z kolejkami ma własność stabilności. Jeżeli elementy x, y są uporządkowane ze względu na k-1 ostatnich cyfr i wpadają do tego samego ‘kubełka’ to po k-tym przebiegu UWAGA nadal są w tym samym porządku. Algorytm Radix. Sort Jeżeli wpadają do różnych kubełków, to po k-tym przebiegumożna są teżk ostatnich stosować uporządkowane ze względu na cyfr. do innych typów danych. x = x k+1 10 k+1 + xk 10 + x’ k y = y k+1 10 k+1 + yk 10 k + y’ x’ < y’, x’, y’< 10 k 2021 -12 -17 Albo xk=yk i wtedy x i y trafiają do tej samej kolejki oraz x poprzedza y Albo xk<yk ale wtedy x trafi do kolejki o mniejszym numerze niż y i w takiej kolejności ukażą się po połączeniu Albo xk>yk ale wtedy x trafi do kolejki o numerze większym niż y i po połączeniu y ukaże się przed x G. Mirkowska, ASD_05 Sortowanie c. d. 21

Demonstracja algorytmów sortowania 4 http: //www. cs. ubc. ca/spider/harrison/Java/sorting- demo. html pokaz 2021 -12 -17 G. Mirkowska, ASD_05 Sortowanie c. d. 22