ALGORYTMY I STRUKTURY DANYCH WYKAD 01 Wprowadzenie Grayna

ALGORYTMY I STRUKTURY DANYCH WYKŁAD 01 Wprowadzenie Grażyna Mirkowska PJWSTK, 2003 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie

Plan wykładu 4 Organizacja wykładu i ćwiczeń z ASD. 4 Cel wykładu. Zapoznanie studentów z podstawowym zestawem algorytmów realizujących zadania typu wyszukiwanie, sortowanie, oraz z najczęściej wykorzystywanymi strukturami danych: stosami, kolejkami, słownikami, kolejkami priorytetowymi i drzewami. Przedstawione zostaną również zasadnicze problemy algorytmiki związane z analizą poprawności i kosztu algorytmów. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 2

O czym będzie mowa w tym wykładzie? 4 Jak formułować (specyfikować) zadania i algorytmy? 4 Jak porównywać algorytmy? 4 Co to jest struktura danych? 4 Jak weryfikować algorytm (program)? 4 Czy zawsze można znaleźć lepsze rozwiązanie? 4 Czy zawsze istnieje algorytm rozwiązujący dany problem? 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 3

Od problemu do jego rozwiązania Sformułowanie zadania. Przykład: Dany jest ciąg liczb. Znaleźć największą z nich. Rozwiązanie problemu. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie Niech max ma wartość równą pierwszemu elementowi ciągu. Porównaj max z kolejnymi elementami ciągu i jeśli spotkasz wartość większą, przyjmij ją jako nową wartość max. 4

Co to jest algorytm? Al-Khowârizmî (Persja, 8 -9 w. n. e. ) (Euklides) Algorytm to metoda Dopóki x różne od y wykonuj: postępowania, która Jeżeli x>y, to odejmij y od x i wynik prowadzi do rozwiązania podstaw na x; W przeciwnym przypadku od y odejmij x i wynik podstaw na y; jakiegoś problemu. Włącz gaz; Zagotuj wodę; Wsyp do szklanki kawę rozpuszczalną; Zalej kawę wrzącą wodą; Dosyp cukru, jeśli lubisz; Poczekaj kilka minut; 3 marzec 2003 koniec dopóki wynikiem jest y Algorytm, to skończony ciąg etapów, które pozwalają przekształcić dane informacje wejściowe w informacje wyjściowe. G. Mirkowska, ASD_01 Wprowadzenie 5

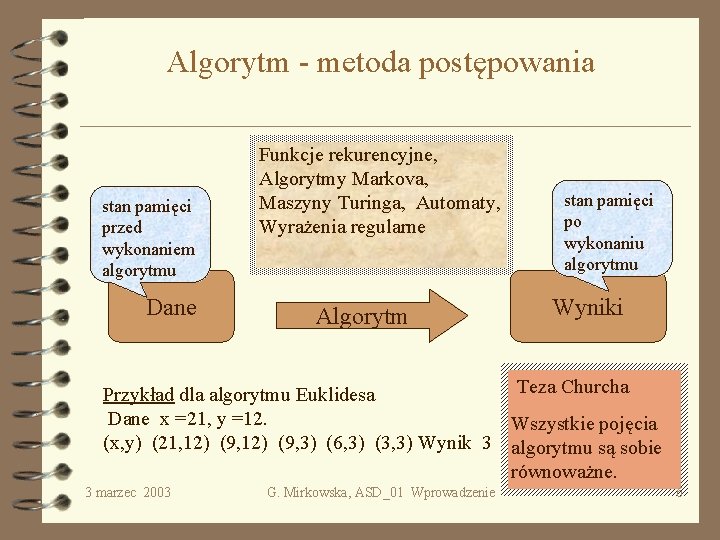
Algorytm - metoda postępowania stan pamięci przed wykonaniem algorytmu Dane Funkcje rekurencyjne, Algorytmy Markova, Maszyny Turinga, Automaty, Wyrażenia regularne Algorytm stan pamięci po wykonaniu algorytmu Wyniki Teza Churcha Przykład dla algorytmu Euklidesa Dane x =21, y =12. Wszystkie pojęcia (x, y) (21, 12) (9, 3) (6, 3) (3, 3) Wynik 3 algorytmu są sobie równoważne. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 6

Jak zapisywać algorytmy? Najczęściej formułujemy zadania i problemy w języku naturalnym, ale język naturalny nie jest dostatecznie precyzyjny. Konstrukcje programotwórcze: if test then {Instrukcje} else{Instrukcje} fi while test do{Instrukcje}od Instrukcja warunkowa Instrukcja pętli. begin Instrukcja {Instrukcja 1}; . . . {Instrukcja n-ta; } złożona. end x : = wyrażenie algebraiczne; 3 marzec 2003 Instrukcja przypisania. G. Mirkowska, ASD_01 Wprowadzenie 7

Jak porównywać algorytmy? • prostota • czytelność • długość kodu • poprawność • czas realizacji • zajętość pamięci 3 marzec 2003 Idealny algorytm to taki, który ma prosty kod, jest napisany w ogólnie dostępnym języku programowania, łatwo go zrozumieć, liczy szybko, nie wymaga dużo miejsca w pamięci i zawsze daje poprawne wyniki. G. Mirkowska, ASD_01 Wprowadzenie 8

Co to jest struktura danych? Sformułowanie problemu algorytmicznego wymaga zwykle określenia środowiska, którego problem dotyczy. Problem „ Znaleźć największy element w danym ciągu” wymaga określenia czym są elementy (np. . Liczbami, zbiorami, dokumentami) i jak się je porównuje. Algorytm, który ma realizować pewną metodę rozwiązania problemu musi znać to środowisko i móc się nim posługiwać. Strukturą danych będziemy nazywali system relacyjny, którego uniwersum określa wartości zmiennych i a operacje i relacje dostarczają narzędzi do realizacji algorytmu. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 9

Przykład 1 while (x y) { Jeśli rozważymy ten algorytm w strukturze liczb całkowitych if x >y podając jako początkowe wartości then x : = x – y x=a i y=b, to algorytm zwróci else y : = y – x jako wynik nwd(a, b) fi } Zawsze daje Czasami daje wynik! return x wynik! Jeśli rozważymy ten algorytm w strukturze, której uniwersum składa się z odcinków na prostej, relacja > pozwala porównać długości odcinków, natomiast operacja – daje w wyniku różnicę odcinków, to algorytm zwraca jako wynik najdłuższy odcinek, który mieści się całkowitą ilość razy w danych początkowo odcinkach. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 10

Poprawność algorytmu Intuicyjnie, poprawność = zgodność z zamierzeniami. Specyfikacją algorytmu nazywać będziemy parę warunków (własności) < wp , wk > Warunek początkowy {wp} Alg {wk} Warunek końcowy Algorytm Alg działający w strukturze danych S jest częściowo poprawny ze względu na specyfikację <wp, wk> wttw dla wszystkich danych spełniających warunek początkowy, jeżeli algorytm zatrzyma się, to uzyskane wyniki spełniają warunek końcowy. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 11

Całkowita poprawność algorytmu wp Alg wk Powiemy, że algorytm Alg działający w strukturze danych S jest całkowicie poprawny ze względu na specyfikację <wp, wk> wttw dla wszystkich danych w strukturze S spełniających warunek początkowy wp, algorytm zatrzymuje się i daje wyniki spełniające warunek końcowy wk. S |= {wp} Alg{wk} 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 12

Przykład 2 Problem: Obliczyć kwadrat liczby naturalnej n. { i: = 1; k : = 1; x: =0; Specyfikacja: while (i n){ warunek początkowy: x : = x + k; n N, n>0 k : = k + 2; i : = i + 1; warunek końcowy: } x jest kwadratem liczby n. return x } Algorytm jest całkowicie poprawny w strukturze liczb naturalnych 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 13

Niezmiennik {i : = 1; k : = 1; x : =0; while (i n){ k=2 i-1, x = S j=1. . i-1 (2 j-1) x : = x + k; x = S j=1. . i (2 j-1) k : = k + 2; i : = i + 1; } return x } k= 2 i+1 x = S j=1. . i-1 (2 j-1), k=2 i-1, i n+1, k = 2 i-1, x = S j=1. . i-1 (2 j-1) 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie Niezmiennikiem pętli nazywać będziemy własność (formułę), która jeśli jest prawdziwa na początku wykonania pętli, to jest również prawdziwa po wykonaniu treści pętli. 14

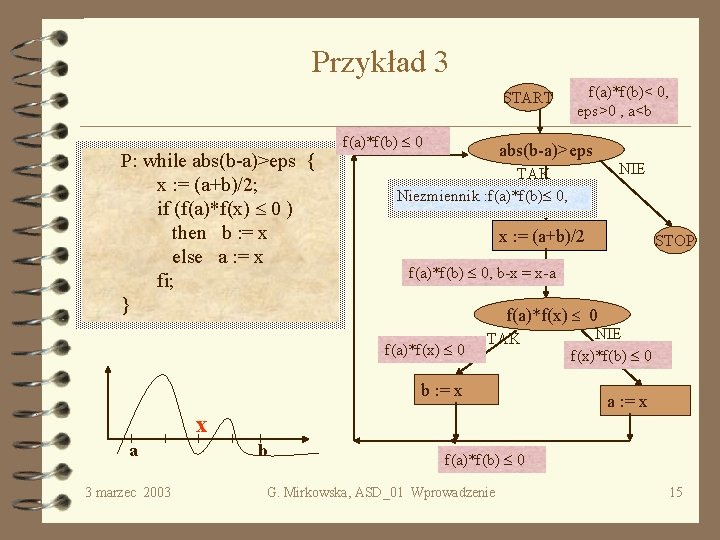
Przykład 3 START P: while abs(b-a)>eps { x : = (a+b)/2; if (f(a)*f(x) 0 ) then b : = x else a : = x fi; } f(a)*f(b) 0 abs(b-a)>eps TAK Niezmiennik : f(a)*f(b) 0, f(a)*f(x) 0 TAK x 3 marzec 2003 STOP f(a)*f(b) 0, b-x = x-a b : = x b NIE x : = (a+b)/2 f(a)*f(x) 0 a f(a)*f(b)< 0, eps>0 , a<b NIE f(x)*f(b) 0 a : = x f(a)*f(b) 0 G. Mirkowska, ASD_01 Wprowadzenie 15

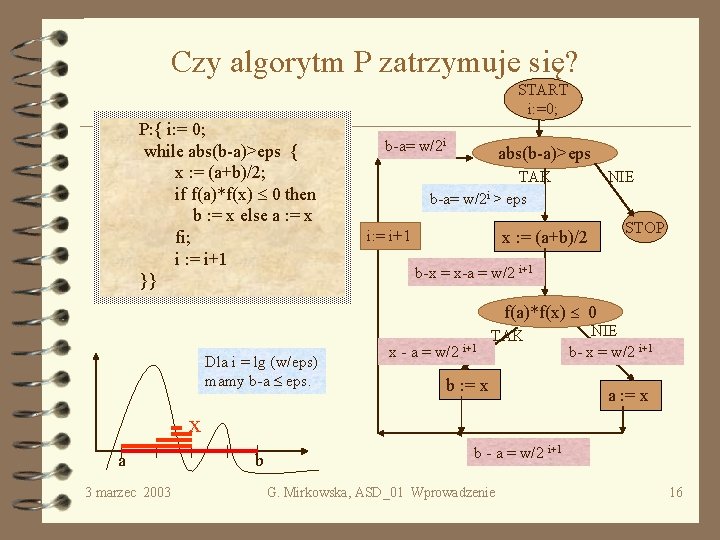
Czy algorytm P zatrzymuje się? START i: =0; P: { i: = 0; while abs(b-a)>eps { x : = (a+b)/2; if f(a)*f(x) 0 then b : = x else a : = x fi; i : = i+1 }} b-a= w/2 i abs(b-a)>eps TAK b-a= w/2 i > eps NIE x : = (a+b)/2 i: = i+1 STOP b-x = x-a = w/2 i+1 f(a)*f(x) 0 Dla i = lg (w/eps) mamy b-a eps. x - a = w/2 i+1 TAK b : = x NIE b- x = w/2 i+1 a : = x x a 3 marzec 2003 b b - a = w/2 i+1 G. Mirkowska, ASD_01 Wprowadzenie 16

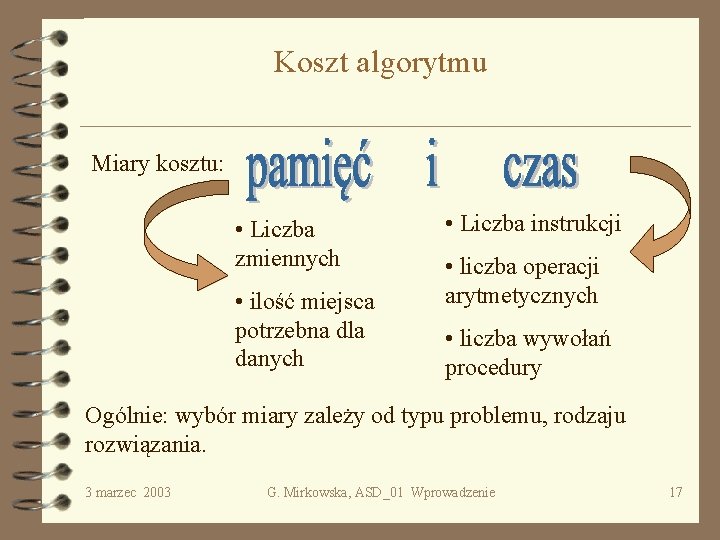
Koszt algorytmu Miary kosztu: • Liczba zmiennych • ilość miejsca potrzebna dla danych • Liczba instrukcji • liczba operacji arytmetycznych • liczba wywołań procedury Ogólnie: wybór miary zależy od typu problemu, rodzaju rozwiązania. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 17

Przykłady Mnożenie macierzy Operacje + , * Wyszukiwanie elementu w tablicy porównywanie Sortowanie Mając dany algorytm, konkretne środowisko i konkretne dane możemy policzyć liczbę operacji dominujących. Koszt algorytmu dla danych d: algorytm 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie dane 18

Złożoność czasowa algorytmu Definicja Złożoność czasowa to liczba operacji dominujących (podstawowych) wykonanych przez algorytm w czasie jego realizacji, wyrażona jako funkcja rozmiaru danych. Niech Dn będzie zbiorem danych rozmiaru n dla pewnego problemu P oraz A algorytmem rozwiązującym problem P. Uwaga 1. Faktyczny czas wykonania algorytmu jest proporcjonalny do W(Alg, n) = sup {t(Alg, d) : d Dn} złożoności czasowej. A(Alg, n) = S{ p(d) * t(Alg, d) : d Dn} 3 marzec 2003 Uwaga 2 Czas wykonania algorytmu jest bardziej interesujący dla dużych n niż dla małych. G. Mirkowska, ASD_01 Wprowadzenie 19

Notacja asymptotyczna Niech f , g : N R+. Powiemy, że g jest co najwyżej rzędu f wttw ( c>0)( no N)( n>no) g(n) c f(n). g = O (f ) Powiemy, że g jest co najmniej rzędu f wttw ( c>0)( no N)( n>no) c*f(n) g(n). g = (f ) 3 marzec 2003 Powiemy, że rzędy funkcji f i g są takie same, wttw g= O(f) i f = O(g). G. Mirkowska, ASD_01 Wprowadzenie 20

Porównywanie rzędów funkcji Przykład 1 Niech f(n)=100 n, g(n)= 2 n+100, h(n) = 0. 1 n 2 +n. Mamy f = O(n) f = (n) g= O(n 2) g = (n) h = O(n 2) = O(n 3 ) h O(n) h = (n) 1. Jeżeli c 0 to f i g są tego samego rzędu. Przykład 2 f(n) = 0. 3 n 3 + 10 n + 100 g(n)= n 3 h(n) = log n 2. Jeżeli c= 0, to f = O(g) oraz f (g). lim n f(n)/g(n)= 0. 3 3. Jeżeli c = + , to f ma rząd większy niż g, g = O(f) i g (f). Czyli f = (g) Lemat (O porównywaniu rzędów funkcji) Niech lim n f(n)/g(n) = c. Wtedy 3 marzec 2003 lim f(n)/h(n) = + Czyli h = O(f), h (f). G. Mirkowska, ASD_01 Wprowadzenie 21

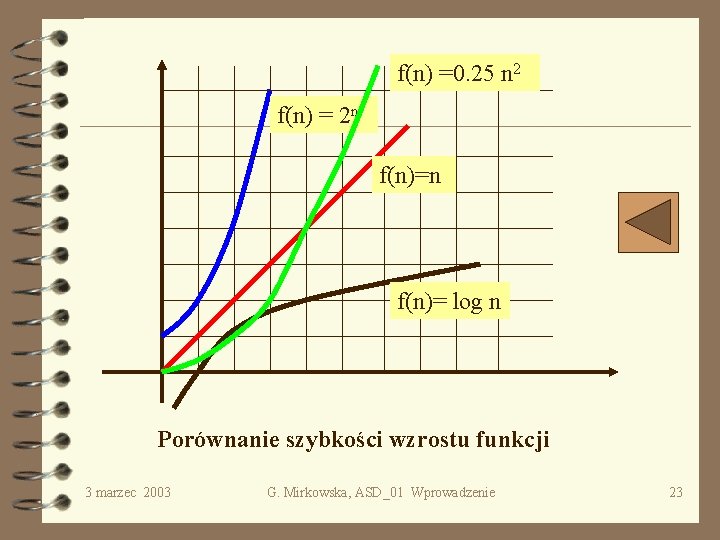
Porównanie szybkości wzrostu funkcji Powiemy, że algorytm Alg ma złożoność czasową wielomianową wykładniczą liniową kwadratową logarytmiczną wttw wttw T(Alg, n)= (n a) a N T(Alg, n) = (a n) a R+ T(Alg, n)= (n) T(Alg, n)= (n 2) T(Alg, n)= (lg n) lg n! = S i=1. . n lg i n lg n 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie lg n 22

f(n) =0. 25 n 2 f(n) = 2 n f(n)= log n Porównanie szybkości wzrostu funkcji 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 23

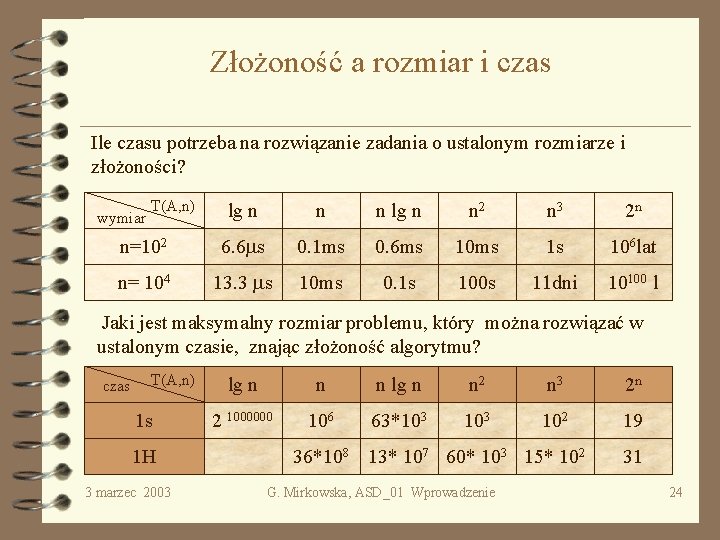
Złożoność a rozmiar i czas Ile czasu potrzeba na rozwiązanie zadania o ustalonym rozmiarze i złożoności? T(A, n) lg n n n lg n n 2 n 3 2 n n=102 6. 6 ms 0. 1 ms 0. 6 ms 10 ms 1 s 106 lat n= 104 13. 3 ms 10 ms 0. 1 s 100 s 11 dni 10100 l wymiar Jaki jest maksymalny rozmiar problemu, który można rozwiązać w ustalonym czasie, znając złożoność algorytmu? czas T(A, n) 1 s 1 H 3 marzec 2003 lg n n n lg n n 2 n 3 2 n 2 1000000 106 63*103 102 19 36*108 13* 107 60* 103 15* 102 G. Mirkowska, ASD_01 Wprowadzenie 31 24

Czy szybkość może pokonać złożoność? Mamy 5 algorytmów A 1, A 2, A 3, A 4, A 5 rozwiązujących ten sam problem. Niech si oznacza maksymalny rozmiar problemu, który można rozwiązać na komputerze 1 przy pomocy algorytmu Ai w ustalonym czasie t. Jaki jest maksymalny rozmiar problemu, który można rozwiązać w tym samym czasie t na komputerze 10 razy szybszym? Komputer 1 Komputer 2 lg n s 1 10 n s 2 10*s 2 n 2 s 3 10*s 3 n 3 s 4 2*s 4 2 n s 5 ? Przykład A 5. Dla komputera 1: T(A 5, s 5)=2 s 5 = t. Dla komputera 2 : T(A 5, s 5)= 2 s 5 = t /10. Szukamy takiego x, że T(A 5, x)= t. Mamy więc 2 x = 10* 2 s 5 = 2 s 5+lg 10. Czyli x = 3. 2 +s 5. 3 marzec 2003 G. Mirkowska, ASD_01 Wprowadzenie 25