A Nave Introduction to TransElliptic Diophantine Equations Donald










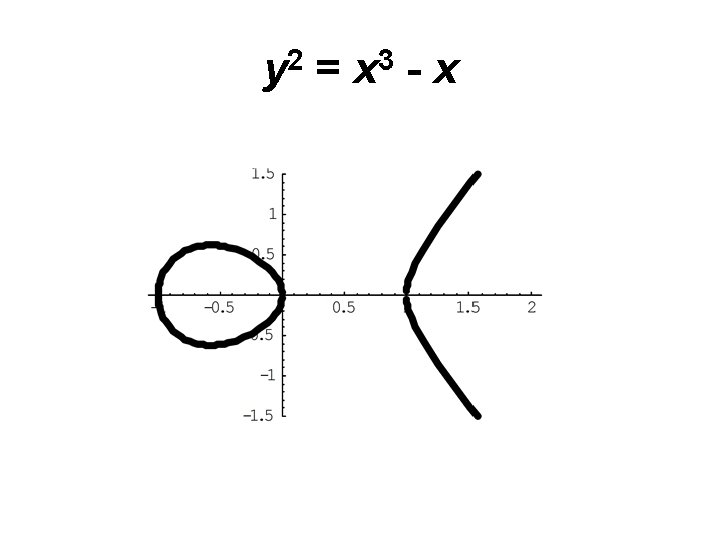


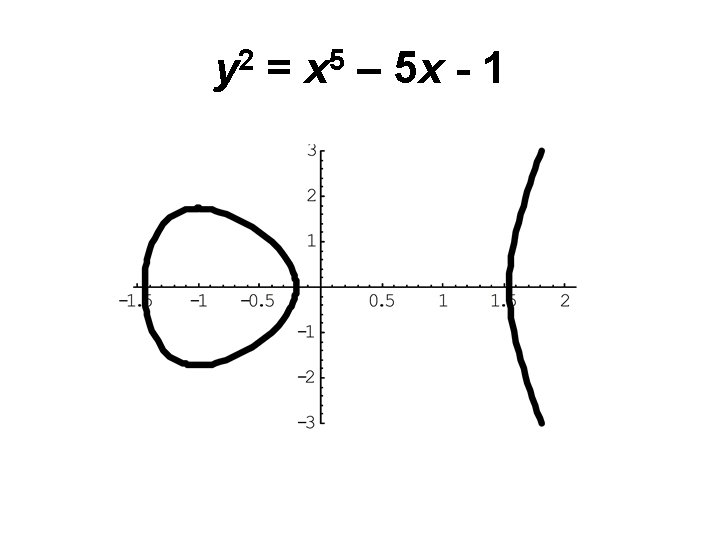



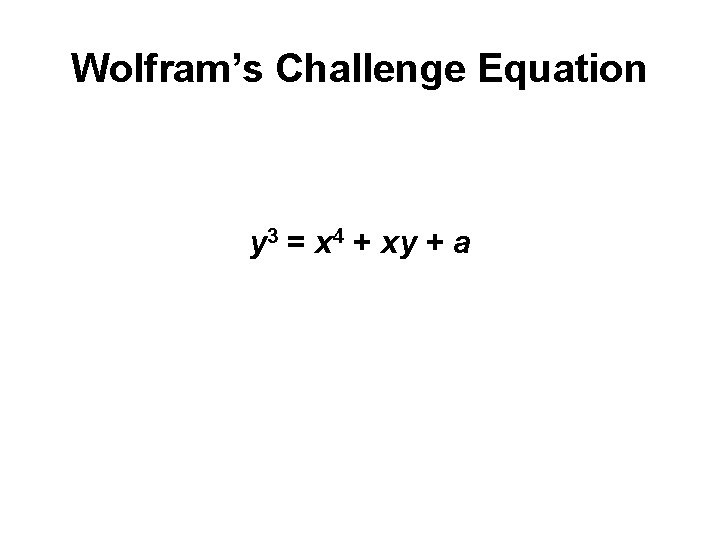
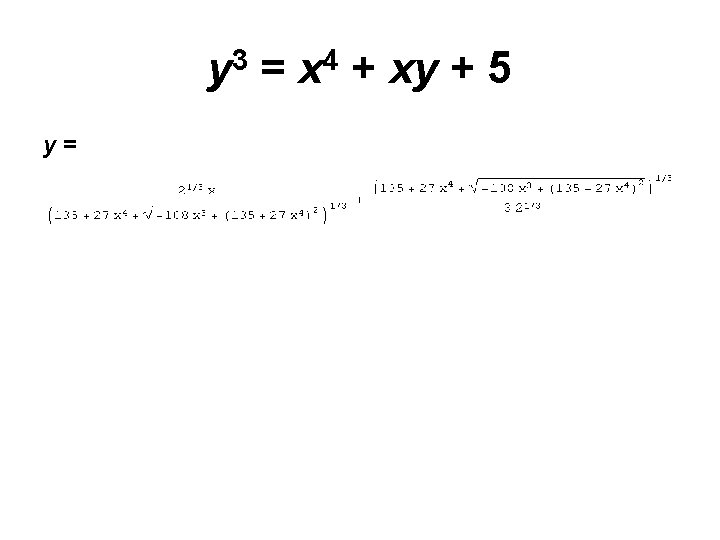




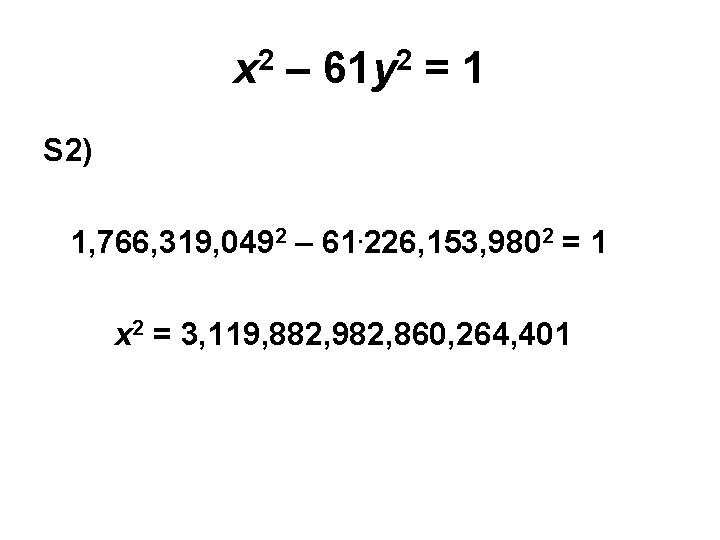



- Slides: 30

A Naïve Introduction to Trans-Elliptic Diophantine Equations Donald E. Hooley Bluffton University Bluffton, Ohio

Outline • • • Linear Diophantine Equations Quadratic Diophantine Equations Hilbert’s 10 th Problem Thue’s Theorem Elliptic Curves Hyperelliptic Curves Superelliptic Curves Trans-elliptic Diophantine Equations Wolfram’s Challenge Equation

Linear Diophantine Equations Q 1) How many beetles and spiders are in a box containing 46 legs?

Linear Diophantine Equations Q 1) How many beetles and spiders are in a box containing 46 legs? 6 x + 8 y = 46

Quadratic Diophantine Equations Q 2) x 2 + y 2 = z 2 Q 3) In 1066 Harold of Saxon claimed 61 squares of men. When he added himself they formed one mighty square.

Quadratic Diophantine Equations Q 2) x 2 + y 2 = z 2 Q 3) In 1066 Harold of Saxon claimed 61 squares of men. When he added himself they formed one mighty square. x 2 – 61 y 2 = 1

Question Q) For which N does x 2 – Ny 2 = 1 have positive solutions?

Hilbert’s Tenth Problem Is there a general algorithm to decide whether a given polynomial Diophantine equation with integer coefficients has a solution?

Thue’s Theorem A polynomial function F(x, y) = a with deg(F) > 2 has only a finite number of solutions.

Elliptic Curves y 2 = p(x) where deg(p) = 3 or 4
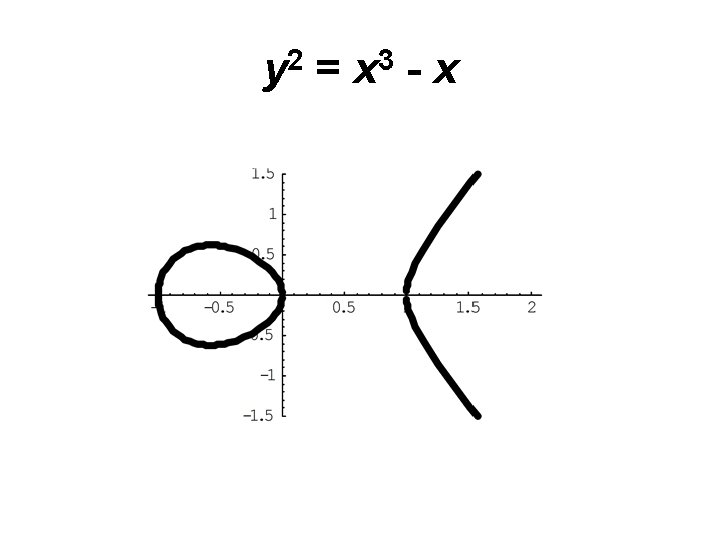
y 2 = x 3 - x


Hyperelliptic Curves y 2 = p(x) where deg(p) > 4
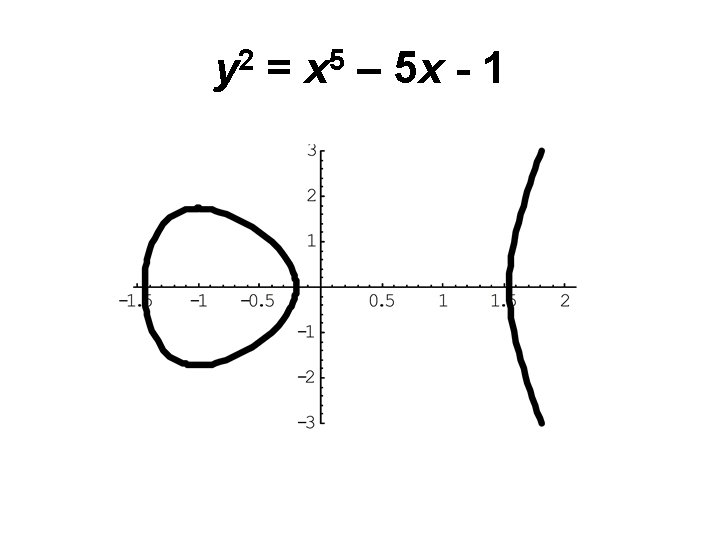
y 2 = x 5 – 5 x - 1

Superelliptic Curves y 3 = p(x) where deg(p) > 3



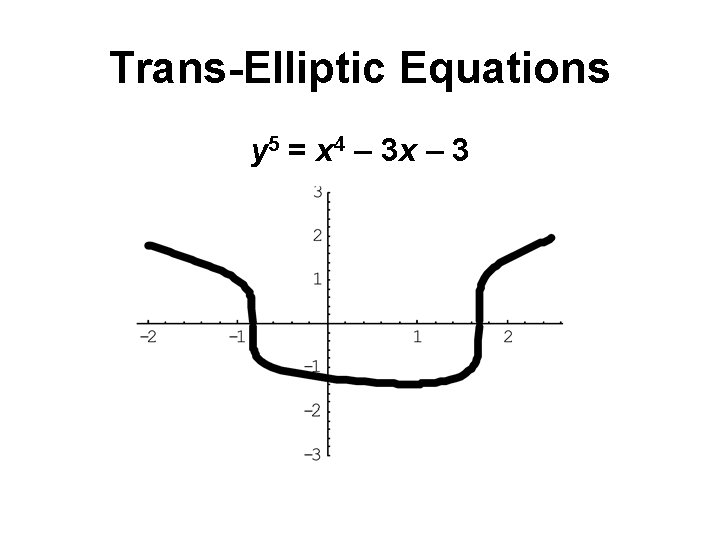
Trans-Elliptic Equations y 5 = x 4 – 3 x – 3

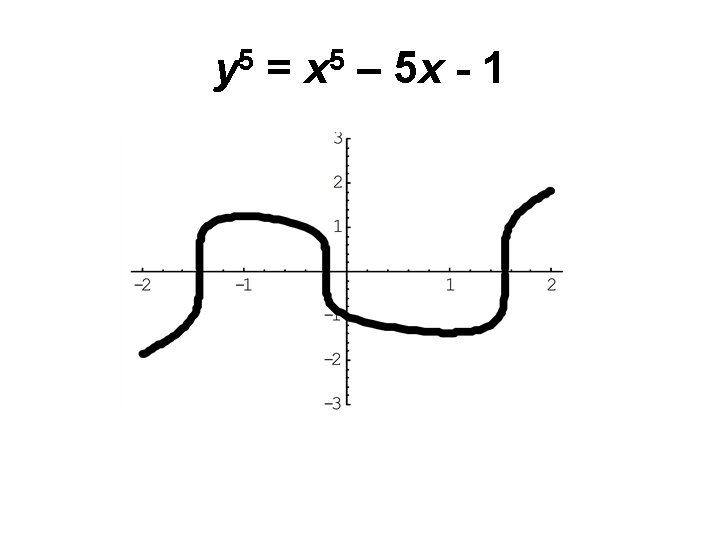
y 5 = x 5 – 5 x - 1
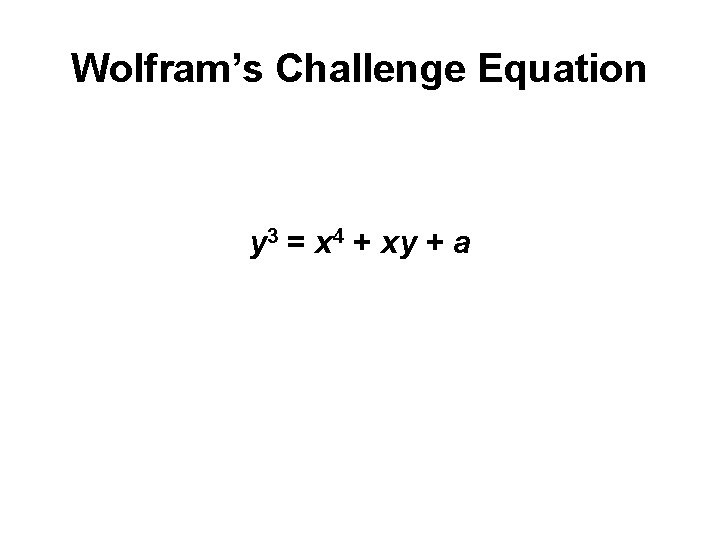
Wolfram’s Challenge Equation y 3 = x 4 + xy + a

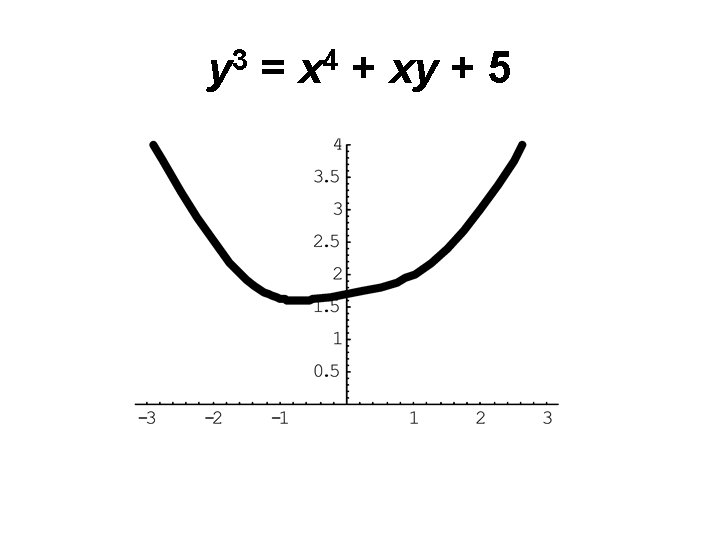
y 3 = x 4 + xy + 5
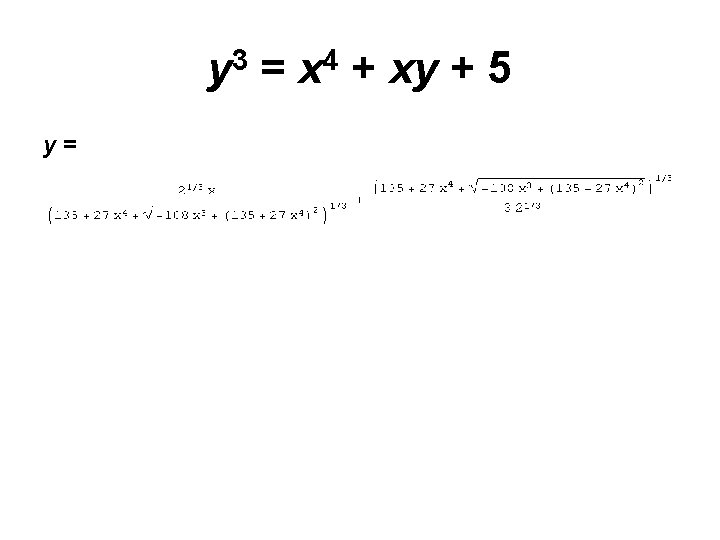
y 3 = x 4 + xy + 5 y=

Questions Q 0) Find distinct positive integers x, y, z so that x 3 + y 3 = z 4. Q 1) The trans-elliptic Diophantine equation y 3 = x 4 + xy + 5 has solutions (1, 2) and (2, 3). Does it have any more solutions?

More Questions Q 2) The trans-elliptic Diophantine equation y 3 = x 4 + xy + 59 has solutions (1, 4), (4, 7) and (5, 9). Does it have any more solutions? Q 3) For which integers a does the Diophantine equation y 3 = x 4 + xy + a have multiple solutions?

References A. H. Beiler, Recreations in the Theory of Numbers – The Queen of Mathematics Entertains, Dover Pub. , Inc. , 1964. Y. Bilu and G. Hanrot, Solving superelliptic Diophantine equations by Baker's method, Compositio Math. 112 (1998) 273 -312. U. Dudley, Elementary Number Theory, W. H. Freeman and Co. , San Francisco, 1969. J. W. Lee, Isomorphism Classes of Picard Curves over Finite Fields, http: //eprint. iacr. org/2003/060. pdf (accessed August 2007). R. J. Stroeker and B. M. M. De Weger, Solving elliptic Diophantine equations: the general cubic case, Acta Arithmetica, LXXXVII. 4 (1999) 339 -365. J. V. Uspensky and M. A. Heaslet, Elementary Number Theory, Mc. Graw-Hill Book Co. , Inc. , 1939. S. Wolfram, A New Kind of Science, Wolfram Media (2002) 1164.

Solutions S 1) 6 x + 8 y = 46 Sol. 3 x + 4 y = 23 3 x 3 mod 4 x 1 mod 4 x = 1 + 4 t so x = 1, 5, … 3(1 + 4 t) + 4 y = 23 3 + 12 t + 4 y = 23 y = (23 – 12 t) / 4 = 5 – 3 t so y = 5, 2, …
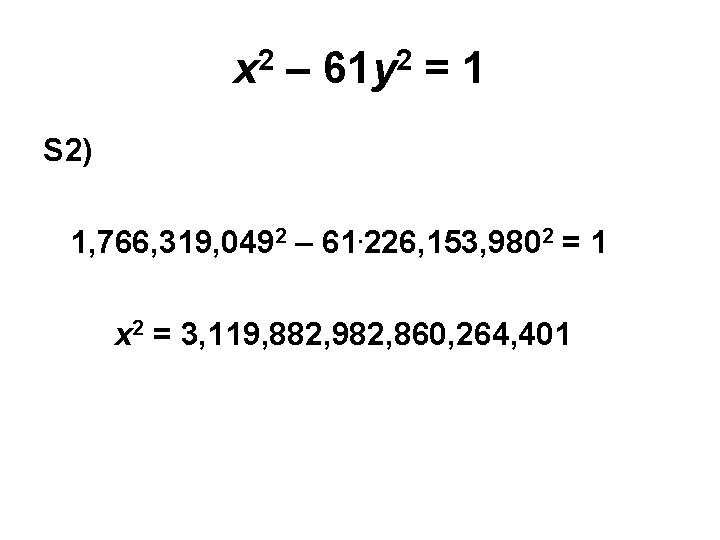
x 2 – 61 y 2 = 1 S 2) 1, 766, 319, 0492 – 61. 226, 153, 9802 = 1 x 2 = 3, 119, 882, 982, 860, 264, 401

x 3 + y 3 = z 4 S 3) No sol. to x 3 + y 3 = z 3 by Fermat. 33 + 53 = 1523. 33 + 1523. 53 = 1523. 152 4563 + 7603 = 1524

y 3 = x 4 + xy + 5 S 4) Methods: 1) Modular arithmetic If x = y = 0 mod 2 then y 3 = 0 mod 2 but x 4 + xy + 5 = 1 mod 2

y 3 = x 4 + xy + 5 2) Convergents of continued fractions 3) Fermat’s method of descent 4) Bound and search Check y 3 - x 4 – xy = 5 No other solutions for -10, 000 < x < 10, 000
 Diophantine equation
Diophantine equation Diophantine approximation
Diophantine approximation Ossatura nave
Ossatura nave Segnali diurni nautica
Segnali diurni nautica Lasse e nude significato
Lasse e nude significato Tipuri de nave fluviale
Tipuri de nave fluviale Nave condizionata dalla propria immersione
Nave condizionata dalla propria immersione Immersione nave
Immersione nave Dislocamento unitario tpc
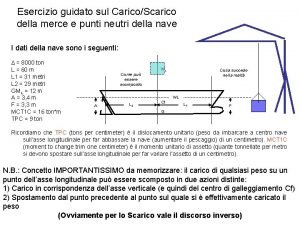
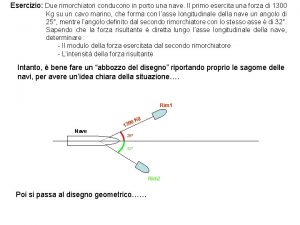
Dislocamento unitario tpc Due rimorchiatori conducono
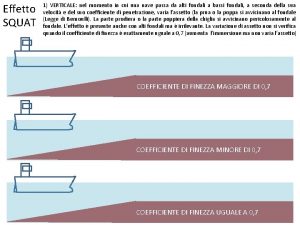
Due rimorchiatori conducono Effetto squat formula
Effetto squat formula Nave neighbor
Nave neighbor Sezione trasversale nave
Sezione trasversale nave Prova di stabilità nave
Prova di stabilità nave Le donne nella divina commedia
Le donne nella divina commedia Abbordi in mare
Abbordi in mare Bordo libero
Bordo libero Caronte parafrasi
Caronte parafrasi Test nave
Test nave Certificato di classe di una nave
Certificato di classe di una nave Opera viva barca
Opera viva barca Titanik potop
Titanik potop Teoria della nave
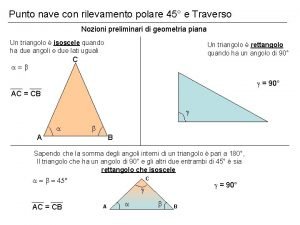
Teoria della nave Rilevamento al traverso
Rilevamento al traverso Lance nave
Lance nave Planeta terra nave em que viajamos
Planeta terra nave em que viajamos Nave de tarsis
Nave de tarsis Parti della nave fenicia
Parti della nave fenicia Nave theme
Nave theme Hyperphysics gsu
Hyperphysics gsu Nave sal da terra
Nave sal da terra