A Generalized Iterated Shrinkage Algorithm for Nonconvex Sparse

A Generalized Iterated Shrinkage Algorithm for Non-convex Sparse Coding Wangmeng Zuo, Deyu Meng, Lei Zhang, Xiangchu Feng, David Zhang ICCV 2013 wmzuo@hit. edu. cn Harbin Institute of Technology

Overview • From L 1 -norm sparse coding to Lp-norm sparse coding – Existing solvers for Lp-minimization • Generalized shrinkage / thresholding function – Algorithm and analysis – Connections with soft/hard-thresholding functions • Generalized Iterated Shrinkage Algorithms • Experimental results 2

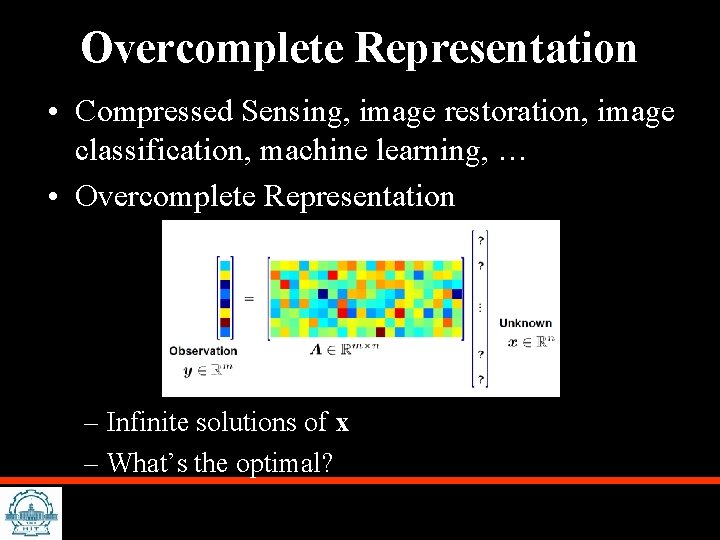
Overcomplete Representation • Compressed Sensing, image restoration, image classification, machine learning, … • Overcomplete Representation – Infinite solutions of x – What’s the optimal?

L 0 -Sparse Coding • Impose some prior (constraint) on x: – Sparser is better • • • Problems – Is the sparsest solution unique? – How can we obtain the optimal solution?

Theory: Uniqueness of Sparse Solution (L 0) • Nonconvex optimization, intractable • Greedy algorithms: matching pursuit (MP), orthogonal matching pursuit (OMP)

Convex Relaxation: L 1 -Sparse Coding • L 1 -Sparse Coding – – • Problems – When L 1 - and L 0 - Sparse Coding have the same solution – Algorithms for L 1 -Sparse Coding 6

Theory: Uniqueness of Sparse Solution (L 1)

Theory: Uniqueness of Sparse Solution (L 1) • Restricted Isometry Property • Convex, various algorithms have been proposed.

Algorithms for L 1 -Sparse Coding • • • Iterative shrinkage/thresholding algorithm Augmented Lagrangian method Accelerated Proximal Gradient Homotopy Primal-Dual Interior-Point Method … Allen Y. Yang, Zihan Zhou, Arvind Ganesh, Shankar Sastry, and Yi Ma. Fast l 1 minimization algorithms for robust face recognition. IEEE Transactions on Image Processing, 2013. Generalized Iterated Shrinkage Algorithm 9

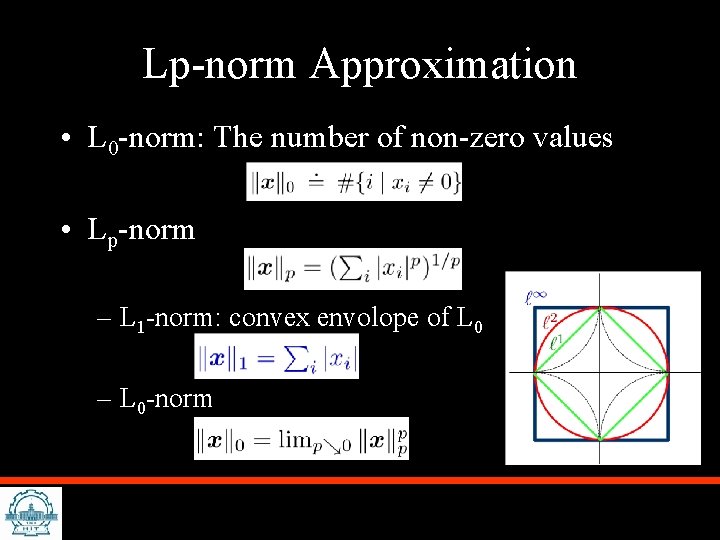
Lp-norm Approximation • L 0 -norm: The number of non-zero values • Lp-norm – L 1 -norm: convex envolope of L 0 – L 0 -norm

Theory: Uniqueness of Sparse Solution (Lp) • Weaker restricted isometry property is sufficient to guarantee perfect recovery in the Lp case. R. Chartrand V. Staneva, "Restricted isometry properties and nonconvex compressive sensing", Inverse Problems, vol. 24, no. 035020, pp. 1 --14, 2008

Existing Lp-sparse coding algorithms • Analytic solutions: Only suitable for some special cases, e. g. , p = 1/2, or p = 1/3. • IRLS, IRL 1, ITM_Lp: would not converge to the global optimal solution even for solving the simplest problem • Lookup table – Efficient, pre-computation

IRLS for Lp-sparse Coding • IRLS – (1) – (2) M. Lai, J. Wang. An unconstrained lq minimization with 0 < q < 1 for sparse solution of under-determined linear systems. SIAM Journal on Optimization, 21(1): 82– 101, 2011. Generalized Iterated Shrinkage Algorithm 13

IRL 1 for Lp-Sparse Coding • IRL 1 – (1) – (2) E. J. Candes, M. Wakin, S. Boyd. Enhancing sparsity by reweighted l 1 minimization. Journal of Fourier Analysis and Applications, 14(5): 877– 905, 2008. Generalized Iterated Shrinkage Algorithm 14

ITM_Lp for Lp-Sparse Coding • ITM_Lp where Root of the equation Y. She. Thresholding-based iterative selection procedures for model selection and shrinkage. Electronic Journal of Statistics, 3: 384– 415, 2009. Generalized Iterated Shrinkage Algorithm 15

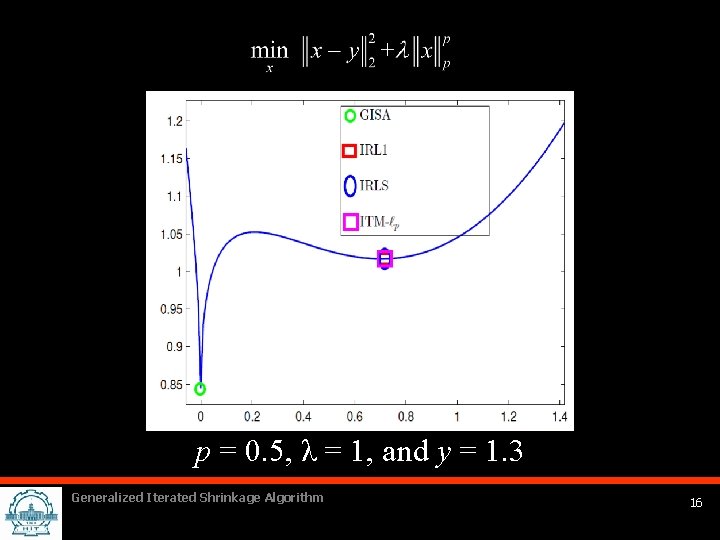
p = 0. 5, λ = 1, and y = 1. 3 Generalized Iterated Shrinkage Algorithm 16

Generalized Shrinkage / Thresholding • Keys of soft-thresholding – Thresholding rule: – Shrinkage rule: • Generalization of soft-thresholding – What’s the thresholding value for Lp? – How to modify the shrinkage rule?

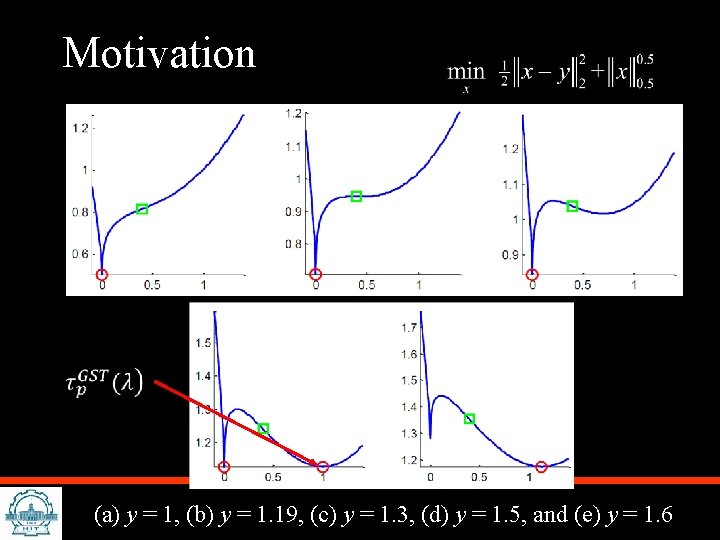
Motivation (a) y = 1, (b) y = 1. 19, (c) y = 1. 3, (d) y = 1. 5, and (e) y = 1. 6

Determining the threshold • The first derivative of the nonzero extreme point is zero • The second derivative of the nonzero extreme point higher than zero • The function value at the nonzero extreme point is equivalent with that at zero

Determining the shrinkage operator • – k = 0, x(k) = |y| – Iterate on k = 0, 1, . . . , J – – k k + 1 – Generalized Iterated Shrinkage Algorithm 20

Generalized Shrinkage / Thresholding Function Generalized Iterated Shrinkage Algorithm 21

GST: Theoretical Analysis

Connections with soft / hardthresholding functions • p = 1: GST is equivalent with soft-thresholding • p = 0: GST is equivalent with hard-thresholding

Generalized Iterated Shrinkage Algorithms • Lp-sparse coding – Gradient descent – Generalized Shrinkage / Thresholding Generalized Iterated Shrinkage Algorithm 24

Comparison with Iterated Shrinkage Algorithms • Iterative Shrinkage / Thresholding – Gradient descent – Soft thresholding

GISA

Sparse gradient based image deconvolution Generalized Iterated Shrinkage Algorithm 27

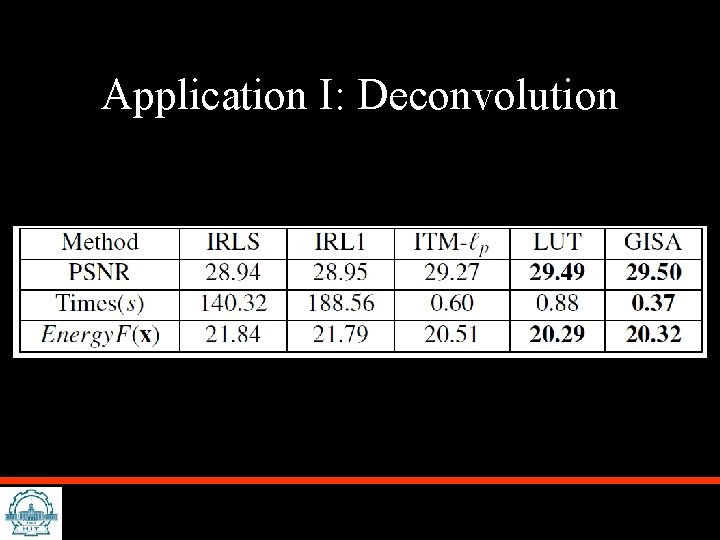
Application I: Deconvolution

Application I: Deconvolution

Application II: Face Recognition • Extended Yale. B

Conclusion • Compared with the state-of-the-art methods, GISA is theoretically solid, easy to understand efficient to implement, and it can converge to a more accurate solution. • Compared with LUT, GISA is more general and does not need to compute and store the look-up tables. • GISA can be readily used to solve the many lp–norm minimization problems in various vision and learning applications. Generalized Iterated Shrinkage Algorithm 32

Looking forward • Applications to other vision problems. • Incorporation of the primal-dual algorithm for better solution • Extension of GISA for constrained Lpminimization, e. g. , 33